Acaban de publicar un artículo nuestro en Sustainable Cities and Society, una de las revistas de mayor impacto científico, ubicada en el primer decil del JCR. En este trabajo se propone un enfoque integrador basado en el ciclo de vida y en métodos de evaluación multicriterio para analizar la vivienda social sostenible. La investigación se enmarca en el proyecto RESILIFE, que dirijo como investigador principal en la Universitat Politècnica de València. A continuación, se presenta un resumen del trabajo.
Acaban de publicar un artículo nuestro en Sustainable Cities and Society, una de las revistas de mayor impacto científico, ubicada en el primer decil del JCR. En este trabajo se propone un enfoque integrador basado en el ciclo de vida y en métodos de evaluación multicriterio para analizar la vivienda social sostenible. La investigación se enmarca en el proyecto RESILIFE, que dirijo como investigador principal en la Universitat Politècnica de València. A continuación, se presenta un resumen del trabajo.
Los principales resultados revelan que el sistema Light Steel Frame (LSF) es la alternativa más sostenible, ya que logra un equilibrio superior entre la eficiencia en el uso de los recursos, la durabilidad y la reducción del mantenimiento. Un descubrimiento crucial es el papel de la dimensión social, que representó casi el 40 % del peso total en la evaluación, por encima de las dimensiones económica y medioambiental. El análisis causal identifica el coste de construcción, la funcionalidad y los agentes de la cadena de valor como los principales factores que condicionan el rendimiento sostenible del resto del sistema.
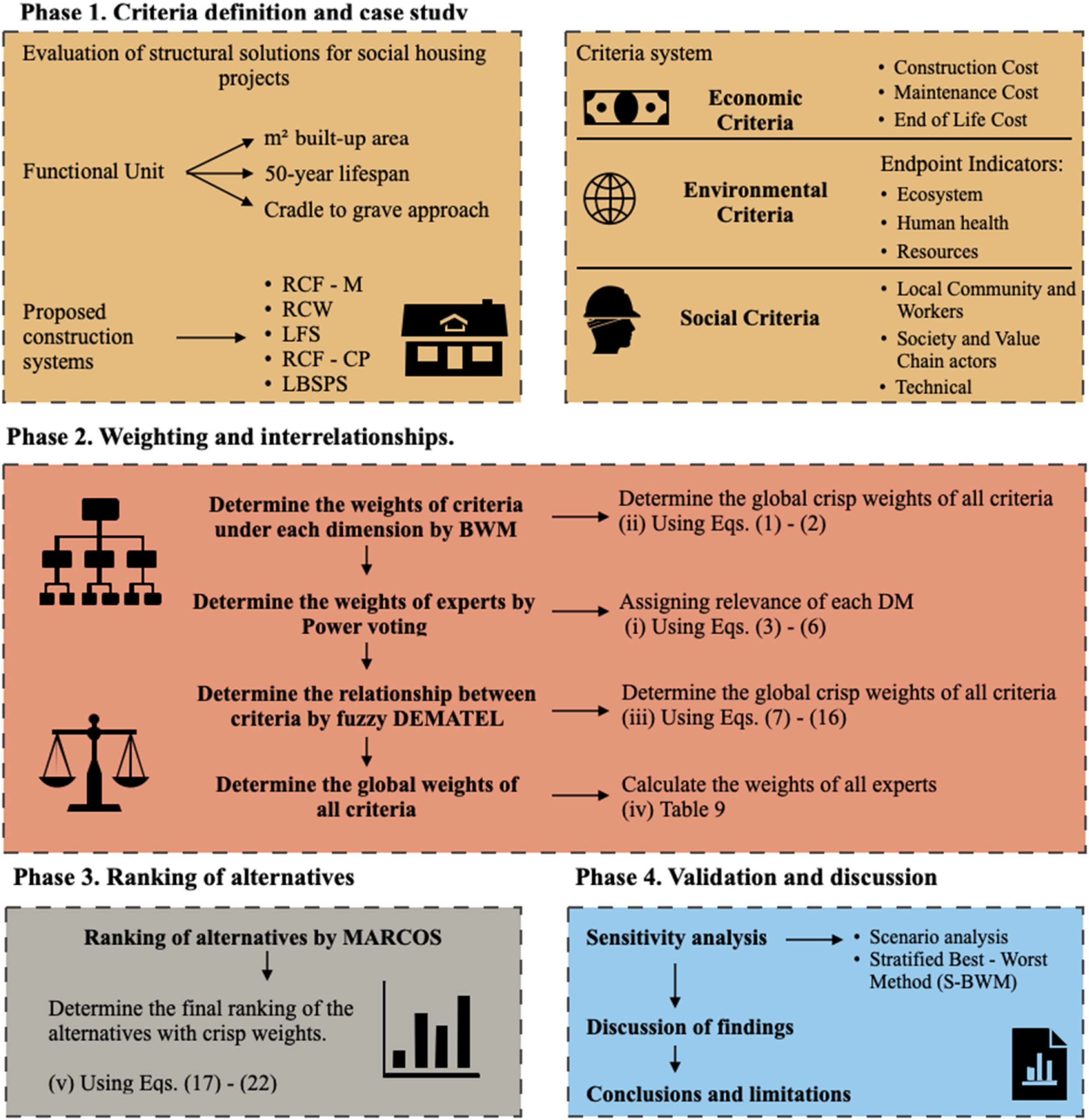
El artículo presenta un marco metodológico integrador que combina evaluaciones basadas en el ciclo de vida —análisis de ciclo de vida (LCA), análisis de coste del ciclo de vida (LCC) y análisis de ciclo de vida estocástico (S-LCA)— con técnicas avanzadas de decisión multicriterio: método mejor-peor (BWM), análisis DEMATEL difuso y análisis MARCOS. Esta integración permite incorporar ponderaciones de expertos, modelar relaciones causales entre criterios y sintetizar resultados frente a soluciones ideales o anti-ideales, lo que aumenta la transparencia en la priorización de alternativas constructivas. Este enfoque se ha aplicado a un caso real de vivienda social en Perú, en el que se han comparado cinco sistemas estructurales representativos: LSF, LBSPS, RCW, RCF-M y RCF-CP. El estudio ha proporcionado pruebas empíricas sobre los costes del ciclo de vida, los impactos ambientales y las prestaciones sociales que respaldan las decisiones de diseño y las políticas.
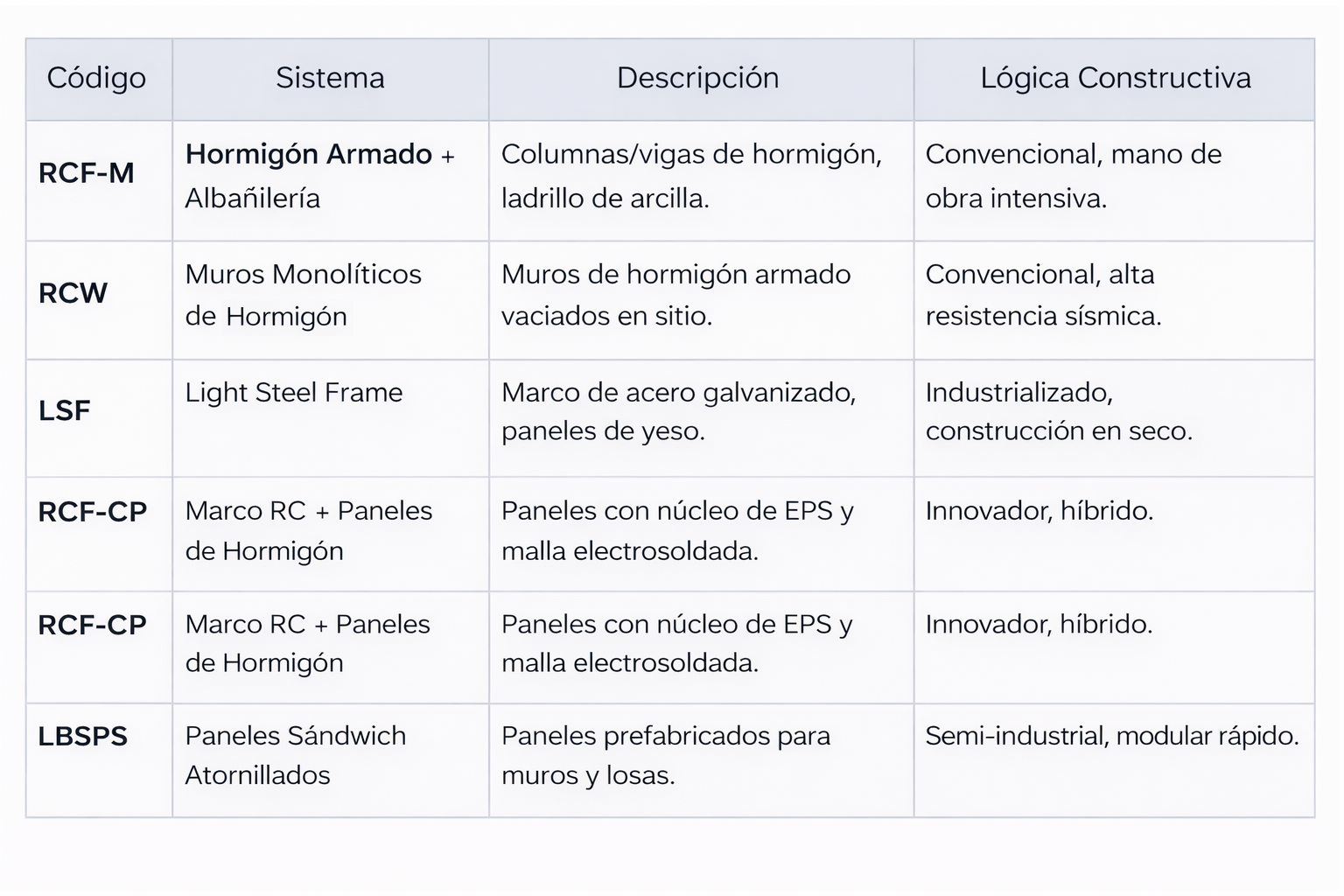
El estudio analiza cinco sistemas constructivos adaptados a contextos de urbanización rápida (específicamente en Lima, Perú), que van desde métodos convencionales hasta industrializados:
Entre las aportaciones metodológicas, la combinación de BWM con una agregación basada en credenciales profesionales reduce la carga de comparación y atenúa los sesgos en la agregación de juicios, mientras que la extensión difusa de DEMATEL permite identificar los criterios que funcionan como impulsores del sistema y los que actúan como receptores. Esta capacidad para distinguir entre causas y efectos permite aclarar qué palancas hay que modificar para lograr efectos amplificados en la sostenibilidad. Por último, la validación cruzada con otros métodos de MCDM y los ensayos de sensibilidad aumentan la confianza en la estabilidad de los resultados.
Discusión de resultados
Los análisis económicos muestran que, en un horizonte de 50 años y por metro cuadrado, los sistemas basados en acero ligero (LSF) tienen los menores costes totales de ciclo de vida, mientras que algunas alternativas prefabricadas, como el LBSPS, tienen los mayores costes de construcción. Estos datos implican que si solo se tiene en cuenta la inversión inicial, se pueden tomar decisiones subóptimas, ya que no se consideran el mantenimiento y el fin de vida.
 En términos ambientales, la evaluación con ReCiPe (endpoint) sitúa al LSF como el sistema con el menor impacto agregado, principalmente debido a su menor intensidad material. Por el contrario, las soluciones con mayor presencia de hormigón y ladrillo presentan una carga superior, especialmente en la dimensión de recursos. Esta diferenciación pone de manifiesto la influencia del perfil material y del proceso de fabricación en la huella medioambiental de la vivienda y sugiere que, en la práctica profesional, se deben priorizar medidas que reduzcan la demanda de materiales energéticamente intensivos en la fase de fabricación.
En términos ambientales, la evaluación con ReCiPe (endpoint) sitúa al LSF como el sistema con el menor impacto agregado, principalmente debido a su menor intensidad material. Por el contrario, las soluciones con mayor presencia de hormigón y ladrillo presentan una carga superior, especialmente en la dimensión de recursos. Esta diferenciación pone de manifiesto la influencia del perfil material y del proceso de fabricación en la huella medioambiental de la vivienda y sugiere que, en la práctica profesional, se deben priorizar medidas que reduzcan la demanda de materiales energéticamente intensivos en la fase de fabricación.
La S-LCA revela una tensión entre la industrialización y la exposición social: las alternativas más industrializadas, como el LSF y el LBSPS, presentan mayores valores de exposición laboral y de funcionalidad exigente, mientras que las tipologías convencionales de hormigón muestran menores riesgos sociales, medidos en Medium Risk Hours. Este resultado indica que la adopción de sistemas industrializados exige prestar atención explícita a la gestión del trabajo, la formación y la coordinación de la cadena de suministro para evitar que los impactos negativos se transfieran al personal y a la comunidad.
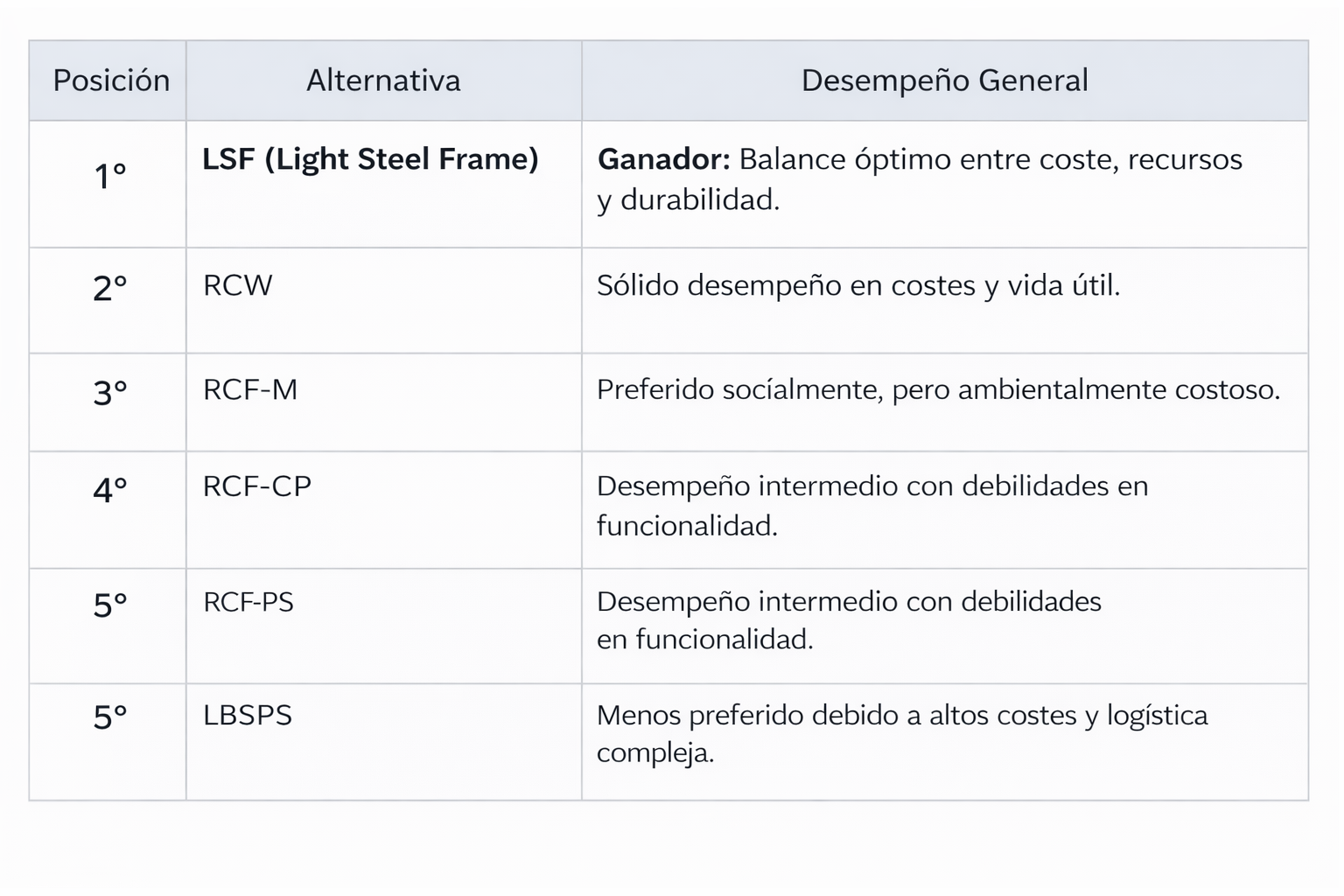
La síntesis mediante MARCOS ubica a LSF como la alternativa mejor valorada en el escenario analizado, seguida de RCW y RCF-M. Los sistemas LBSPS y RCF-CP quedan en posiciones inferiores. Las pruebas de sensibilidad (variación de los pesos de ±15 %, escenarios de distancia de transporte y estratificación de expertos) muestran que el orden general se mantiene, lo que indica cierta robustez frente a perturbaciones razonables en los supuestos. Estos resultados permiten extraer una conclusión práctica: en contextos con características similares a las del caso estudiado, las soluciones ligeras industrializadas pueden mejorar la relación entre coste, impacto ambiental y rendimiento técnico, siempre que se gestionen adecuadamente los aspectos sociales y de ejecución.
Un aspecto metodológico de interés es la identificación de los criterios causales. La técnica DEMATEL identifica el coste de construcción, la funcionalidad y las interacciones con la cadena de valor como criterios que inciden en el resto del sistema, mientras que los indicadores ambientales, como la salud humana y la conservación de los ecosistemas, se presentan principalmente como efectos. Esto sugiere que las intervenciones en los costes de construcción y en la organización funcional pueden provocar mejoras indirectas en la sostenibilidad ambiental y social, lo cual resulta relevante al diseñar políticas y contratos que incentiven las prácticas integradas.
Futuras líneas de investigación
Una línea de trabajo inmediata consiste en ampliar la diversidad y el tamaño del panel de agentes consultados para captar las variaciones en las prioridades y las competencias profesionales. Esto permitiría evaluar la sensibilidad de las ponderaciones y mejorar la representatividad social del proceso. Otra opción es trasladar y recalibrar el marco a otros contextos geográficos y tipologías constructivas, como viviendas de mayor altura o equipamientos públicos, para evaluar la transferibilidad de la clasificación y de la estructura causal identificada en este estudio.
En el ámbito técnico, utilizar datos primarios de obras reales en lugar de bases de datos secundarias aumentará la fiabilidad de la evaluación del ciclo de vida (LCA) y del análisis del ciclo de vida (S-LCA) y mejorará la precisión de los modelos de coste del ciclo de vida (LCC). La incorporación de enfoques dinámicos, como la LCA dinámica o las simulaciones acopladas a plataformas BIM, puede facilitar las evaluaciones en etapas iniciales y permitir análisis de sensibilidad más detallados relacionados con la sustitución de componentes, las reparaciones y las evoluciones tecnológicas. Asimismo, explorar técnicas de optimización multiobjetivo que vinculen explícitamente las restricciones económicas con las metas ambientales y sociales podría proporcionar soluciones de diseño más operativas para promotores y organismos públicos.
Desde la perspectiva social, investigar intervenciones concretas de capacitación, reorganización de procesos y de contratos que reduzcan la exposición de los trabajadores a los sistemas industrializados aportará pruebas sobre cómo mantener los beneficios ambientales y económicos sin incrementar los impactos sociales. Por último, el estudio de la interacción entre políticas públicas, incentivos financieros y la adopción tecnológica ofrecerá información útil para diseñar instrumentos que favorezcan soluciones constructivas más equilibradas en el marco de los programas de vivienda social.
Conclusión
El estudio proporciona un marco metodológico replicable y sólido que combina la evaluación del ciclo de vida con técnicas multicriterio capaces de representar las interdependencias y la incertidumbre. Los resultados empíricos indican que, en el caso analizado, las soluciones ligeras industrializadas presentan ventajas en términos de coste y de huella ambiental, aunque se requieren medidas específicas para reducir los riesgos sociales derivados de su ejecución. La metodología y los resultados obtenidos sientan las bases para orientar las políticas y las decisiones de los proyectos y ponen de manifiesto la necesidad de ampliar los datos primarios, diversificar la muestra de expertos y conectar el análisis con herramientas digitales de diseño y gestión.
Referencia:
LUQUE CASTILLO, X.; YEPES-BELLVER, L.; YEPES, V. (2026). Towards Sustainable Social Housing: An Integrative Life Cycle and Multi-Criteria Approach. Sustainable Cities and Society, 137, 107164. DOI:10.1016/j.scs.2026.107164
Dejo a continuación el artículo completo, ya que está publicado en abierto.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.