¿Por qué algunos estudiantes aprenden de verdad y otros solo memorizan para el examen?
¿Por qué algunos estudiantes aprenden de verdad y otros solo memorizan para el examen?
Todos nos hemos hecho esta pregunta, ya sea como docentes o como estudiantes: ¿por qué el conocimiento que con tanto esfuerzo se imparte en las aulas universitarias parece evaporarse justo después del examen final? La respuesta no radica en estudiar más horas ni en cubrir más temario, sino en cómo diseñamos la experiencia de aprendizaje.
La investigación en educación superior ha revelado principios clave para una «buena docencia» que a menudo contradicen las prácticas más arraigadas. No se trata de opiniones, sino de conclusiones basadas en décadas de estudio sobre el aprendizaje humano. Este artículo resume cuatro de las ideas más impactantes y transformadoras extraídas de marcos de innovación como los Proyectos de Innovación y Mejora Educativa (PIME) de la Universitat Politècnica de València, que se basan en estas investigaciones para redefinir la calidad docente.
1. Diseñar el currículo «hacia atrás»: la revolución del diseño inverso.
Tradicionalmente, la planificación de una asignatura comienza con una pregunta: ¿qué temas vamos a abordar? Se elige un libro de texto, se secuencian los capítulos y se diseñan actividades para cada uno de ellos. Sin embargo, este enfoque tiene un problema fundamental: se centra en los inputs (lo que el profesor enseña) y no en los outputs (lo que el estudiante debe ser capaz de hacer).
El concepto de «diseño inverso» (Backward Design), propuesto por Wiggins y McTighe, le da la vuelta a esta lógica. La idea, radicalmente simple, pero poderosa, es que la planificación curricular debe empezar por el final, es decir, definiendo primero los resultados de aprendizaje deseados: ¿qué comprensiones profundas y qué competencias clave queremos que nuestros estudiantes adquieran con la asignatura? Una vez que tenemos esa meta clara, el segundo paso es determinar qué evidencias (evaluaciones) nos demostrarán que la han alcanzado. Solo entonces, como tercer y último paso, se diseñan las actividades de aprendizaje e instrucción.
Este enfoque garantiza un «alineamiento constructivo» (un concepto acuñado por John Biggs), en el que las actividades que realizan los estudiantes y los métodos de evaluación están lógicamente conectados con los objetivos de aprendizaje. No hay nada al azar: cada elemento del curso tiene un propósito claro.
«Nuestras lecciones, unidades y cursos deben inferirse lógicamente de los resultados que buscamos, no derivarse de los métodos, libros y actividades con los que nos sentimos más cómodos. El currículo debe exponer las formas más eficaces de lograr resultados específicos. En resumen, los mejores diseños parten de los aprendizajes buscados».
Este cambio de perspectiva obliga al docente a actuar como un arquitecto del aprendizaje, centrándose en la transferencia y la comprensión reales de los contenidos, en lugar de en la mera cobertura de estos. Así, la planificación de una clase deja de ser una simple lista de contenidos para convertirse en un acto intencionado de diseño orientado al éxito del estudiante. Con un diseño curricular que parte del fin, el docente ya no se pregunta «¿qué voy a enseñar hoy?», sino «¿qué experiencia debo diseñar para que mis estudiantes logren el objetivo?», lo que nos lleva a un cambio de paradigma fundamental en nuestra propia misión.
2. El gran cambio de paradigma: pasar de enseñar a provocar el aprendizaje.
Si el primer punto cambia la forma en que planificamos, el segundo redefine nuestra misión como docentes. En un influyente artículo de 1995, Barr y Tagg acuñaron la expresión “shift from teaching to learning” (el cambio de la enseñanza al aprendizaje) para describir un cambio de paradigma fundamental.
Este cambio propone que la misión del profesorado universitario no se limita a transmitir información, sino a diseñar experiencias y entornos que permitan a los estudiantes aprender por sí mismos. El foco se desplaza de la figura del profesor y de su discurso hacia la actividad del estudiante y su proceso de construcción del conocimiento. Ya no se trata de ser un «sabio en el estrado», sino de un «guía en el camino».
«Ahora vemos que nuestra misión no es instruir, sino provocar el aprendizaje de cada uno de los estudiantes mediante el método que mejor les funcione».
Esta idea tiene implicaciones profundas. Nos obliga a preguntarnos constantemente qué están haciendo los estudiantes para aprender. Este cambio nos libera de la presión de ser meros oradores para convertirnos en facilitadores eficaces del desarrollo de los demás. Si nuestra misión es provocar aprendizaje, la siguiente pregunta es inevitable: ¿aprendizaje de qué? No se trata de aprender a repetir, sino de aprender a pensar, actuar y ser, que es la verdadera esencia de la competencia.
3. La verdadera competencia consiste en pensar y actuar como un experto.
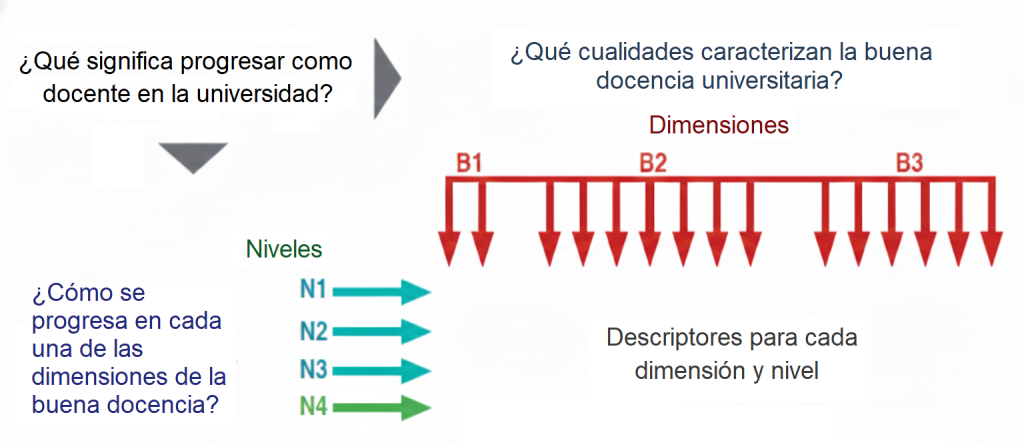
¿Qué significa ser un ingeniero, un médico o un historiador competente? La noción de «competencia» ha evolucionado significativamente y comprender esta evolución es crucial para diseñar un aprendizaje valioso. Podemos identificar tres niveles de concepción:
- Nivel 1: competencia como conocimiento. En su versión más básica, se piensa que una persona competente es quien sabe «más», quien acumula más conocimientos académicos sobre un tema. El foco está en la reproducción de la información.
- Nivel 2: competencia como aplicación. Un paso más allá, se considera que una persona competente es aquella que sabe aplicar el conocimiento teórico a problemas prácticos «reales». En este nivel, la transferencia del conocimiento se concibe como relativamente directa: primero se aprende la teoría y luego se aplica.
- Nivel 3: competencia como gestión de la complejidad. Esta es la concepción más avanzada y la que se persigue en la educación superior de calidad. Una persona verdaderamente competente es aquella que sabe afrontar situaciones nuevas, confusas y complejas, razonando y actuando como lo haría un experto en su campo.
El verdadero desafío docente no consiste en la «transferencia» de conocimientos de un contexto a otro, sino en desarrollar las formas de pensar y actuar propias de una disciplina (ways of thinking and practising, un concepto clave de McCune y Hounsell (2005) y de Entwistle (2007). Se trata de enseñar a los estudiantes a pensar como un biólogo, a argumentar como un jurista o a diseñar como un arquitecto. Por tanto, nuestro objetivo no es que el estudiante sepa sobre nuestra disciplina, sino que se convierta en un incipiente practicante de ella.
4. El «student engagement»: la métrica definitiva del aprendizaje.
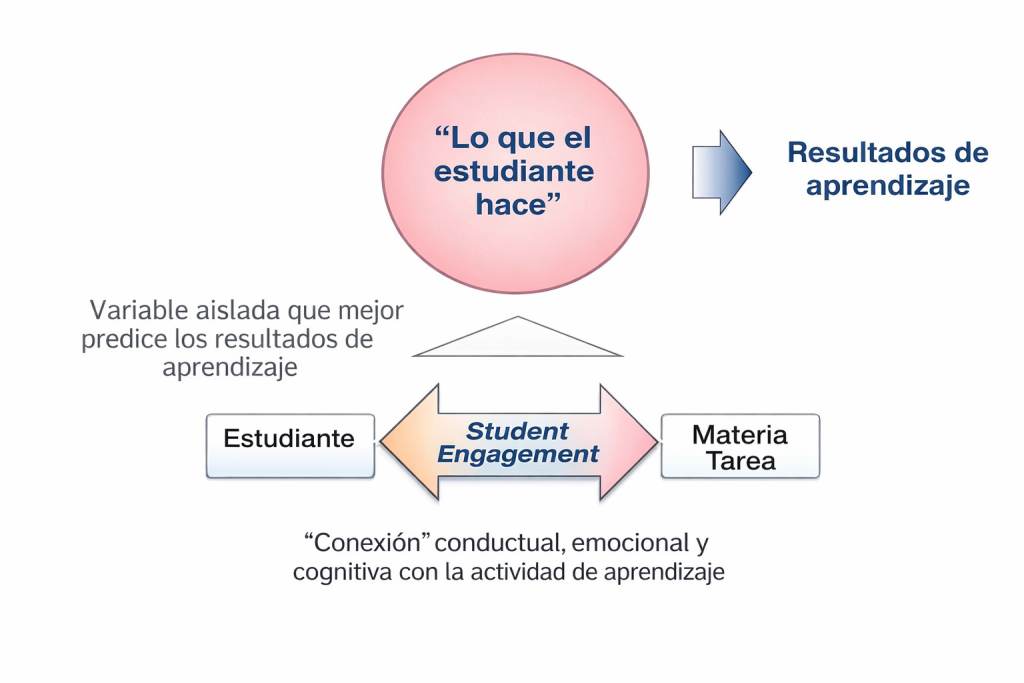
Si el aprendizaje requiere que los estudiantes desarrollen formas complejas de pensamiento, ¿cómo podemos fomentarlo? La respuesta se halla en un concepto que se ha convertido en el principal foco de atención de la investigación educativa: el engagement del estudiante.
La evidencia es abrumadora: según una influyente revisión de la literatura realizada por V. Trowler (2010) señala una «correlación robusta» entre el grado de implicación del estudiante en actividades académicas valiosas y resultados positivos, como el éxito, la satisfacción y la persistencia en los estudios. Da igual lo brillante que sea una lección magistral; si el estudiante no está mentalmente implicado, no se producirá un aprendizaje profundo. Como resumieron Chickering y Gamson en 1987:
«El aprendizaje no es un deporte de espectadores. Los estudiantes no aprenden demasiado: simplemente se sientan en clase a escuchar al profesorado, memorizan tareas prefabricadas y repiten respuestas. Deben hablar sobre lo que están aprendiendo, escribir sobre ello, relacionarlo con experiencias pasadas y aplicarlo a sus vidas cotidianas. Deben hacer de lo que aprenden parte de sí mismos».
 Es importante distinguir entre el aprendizaje «activo» (en el que el estudiante simplemente «hace cosas») y el aprendizaje «constructivo», un concepto desarrollado por Chi (2009), en el que se le pide al estudiante que vaya «más allá» del material de partida. El aprendizaje meramente «activo» podría consistir en aplicar una fórmula a un problema tipo. En cambio, el aprendizaje «constructivo» exige una elaboración cognitiva superior, como confrontar críticamente dos teorías alternativas, diseñar un experimento para confirmar una hipótesis o formular nuevas preguntas sobre un fenómeno. Es en esta construcción donde se produce un aprendizaje profundo y la implicación del estudiante se convierte en verdaderamente productiva.
Es importante distinguir entre el aprendizaje «activo» (en el que el estudiante simplemente «hace cosas») y el aprendizaje «constructivo», un concepto desarrollado por Chi (2009), en el que se le pide al estudiante que vaya «más allá» del material de partida. El aprendizaje meramente «activo» podría consistir en aplicar una fórmula a un problema tipo. En cambio, el aprendizaje «constructivo» exige una elaboración cognitiva superior, como confrontar críticamente dos teorías alternativas, diseñar un experimento para confirmar una hipótesis o formular nuevas preguntas sobre un fenómeno. Es en esta construcción donde se produce un aprendizaje profundo y la implicación del estudiante se convierte en verdaderamente productiva.
¿Diseñamos clases o diseñamos aprendizaje?
Estas cuatro ideas no son consejos aislados, sino los engranajes de un mismo motor pedagógico. El diseño inverso (idea 1) nos proporciona el mapa. El cambio de paradigma hacia el aprendizaje (idea 2) nos brinda la brújula. El desarrollo del pensamiento experto (idea 3) es nuestro destino. Y el Student engagement (idea 4) es el combustible que nos lleva hasta él.
En tu próxima clase o sesión de estudio, pregúntate: ¿qué pequeño cambio podrías hacer para pasar de «cubrir material» a «provocar un aprendizaje» real y duradero?
En esta conversación podéis escuchar lo más importante de este cambio de enfoque.
En este vídeo se recogen las ideas más interesantes del tema.
Referencias:
Barr, R. B., & Tagg, J. (1995). From teaching to learning: A new paradigm for undergraduate education. Change: The Magazine of Higher Learning, 27(6), 13–25.
Chi, M. T. H. (2009). Active-constructive-interactive: A conceptual framework for differentiating learning activities. Topics in Cognitive Science, 1(1), 73–105. https://doi.org/10.1111/j.1756-8765.2008.01005.x
Chickering, A. W., & Gamson, Z. F. (1987). Seven principles for good practice in undergraduate education. AAHE bulletin, 3, 7.
McCune, V., & Hounsell, D. (2005). The development of students’ ways of thinking and practising in three final-year biology courses. Higher Education, 49(1–2), 255–289. https://doi.org/10.1007/s10734-004-6666-0
Trowler, V. (2010). Student engagement literature review. The higher education academy, 11(1), 1-15.
Wiggins, G., & McTighe, J. (1998). Backward design. In Understanding by design (pp. 13–34). ASCD.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.