Os presento un Manual de Referencia sobre la fabricación y la puesta en obra del hormigón. Este libro ofrece una visión integral de la fabricación y la puesta en obra del hormigón, tanto en el ámbito de la edificación como en el de la ingeniería civil. Aborda los equipos y procesos asociados a la preparación del hormigón —incluidas las centrales de hormigonado—, su transporte, vertido, compactación y curado, así como los hormigones especiales, los pavimentos de hormigón para carreteras y el hormigón pretensado. La principal aportación de la obra es su enfoque constructivo, apoyado en abundante material gráfico —fotografías e ilustraciones— que refuerza y clarifica las explicaciones. El texto se completa con una amplia bibliografía, cuestiones de autoevaluación con sus respuestas y problemas resueltos que facilitan la consolidación de los conceptos fundamentales. Concebido como libro de texto para estudiantes de ingeniería y arquitectura, ofrece una orientación práctica clara para la construcción. Al mismo tiempo, está estructurado como un manual de consulta para profesionales vinculados al proyecto y a la ejecución de obras, complementando los contenidos de otros textos de carácter estructural o geotécnico, habitualmente más centrados en el desarrollo teórico y en el cálculo.
El libro está editado a todo color, con 452 páginas, 214 fotografías y dibujos, así como 200 preguntas tipo test (con sus respuestas) y un total de 19 ejercicios totalmente resueltos.
Víctor Yepes Piqueras. Doctor Ingeniero de Caminos, Canales y Puertos. Catedrático de Universidad del Departamento de Ingeniería de la Construcción y Proyectos de Ingeniería Civil de la Universitat Politècnica de València. Consejero del Sector de Docencia e Investigación del Colegio de Ingenieros de Caminos, Canales y Puertos. Número 1 de su promoción, ha desarrollado su vida profesional en empresas constructoras, en el sector público y en el ámbito universitario. Ha recibido el Premio a la Excelencia Docente del Consejo Social, así como el Premio a la Trayectoria Excelente en Investigación y el Premio al Impacto Excelente en Investigación, ambos otorgados por la Universitat Politècnica de València. Es investigador del Instituto de Ciencia y Tecnología del Hormigón (ICITECH) y profesor visitante en la Pontificia Universidad Católica de Chile. Ha sido director académico del Máster Universitario en Ingeniería del Hormigón (acreditado con el sello EUR-ACE). Imparte docencia en asignaturas de grado y posgrado relacionadas con los procedimientos de construcción y gestión de obras, la calidad e innovación, los modelos predictivos y la optimización en la ingeniería. Sus líneas de investigación actuales se centran en la optimización multiobjetivo, la sostenibilidad y el análisis de ciclo de vida de puentes y estructuras de hormigón.
Referencia:
YEPES, V. (2026). Fabricación y puesta en obra del hormigón. Colección Manual de Referencia, serie Ingeniería Civil. Editorial Universitat Politècnica de València, 452 pp. Ref. 441. ISBN: 978-84-1396-418-8
A continuación, os podéis descargar las primeras páginas del libro y su índice:
A simple vista, una carretera de hormigón parece una superficie estática y monótona. Sin embargo, tras esa apariencia gris se esconde un sistema de ingeniería de alta precisión diseñado para resistir condiciones extremas que desintegrarían cualquier estructura convencional. ¿Por qué algunas carreteras mantienen su integridad durante décadas, mientras que otras fallan prematuramente?
La respuesta no solo radica en el material, sino también en que el hormigón para pavimentos opera bajo reglas físicas y químicas radicalmente distintas de las de la construcción tradicional. Basándonos en la documentación de las referencias, exploraremos la ciencia invisible que permite que estas estructuras soporten millones de toneladas de carga y la inclemencia del clima.
Para los que estéis interesados en ampliar información sobre este tema de los pavimentos de hormigón en carreteras, podéis consultar otras entradas en este mismo blog en el siguiente enlace:
Flexotracción: cuando el hormigón debe aprender a «doblarse»
En la construcción de edificios, el hormigón destaca por su resistencia a la compresión, ya que su función es soportar cargas verticales. Sin embargo, en una carretera, la regla de oro cambia: lo que realmente importa es la flexotracción. Mientras un pilar se comprime, una losa de pavimento actúa como una viga apoyada sobre el suelo que debe «flexionar» ante el paso de los neumáticos.
La normativa técnica española (PG-3) es estricta: para pavimentos se utilizan hormigones HF-3,5, HF-4,0 y HF-4,5, donde el número indica su resistencia mínima a la flexotracción en megapascales (MPa) a los 28 días. Esta capacidad es vital, ya que, como señalan los expertos en la materia, las fisuras aparecen siempre donde la resistencia a tracción es menor que en el resto del material o en una zona donde se presenta una mayor concentración de tensiones.
«Las fisuras aparecen siempre donde la resistencia a tracción es menor que en el resto del material o en una zona donde se presenta una mayor concentración de tensiones».
Por ello, el hormigón vial debe ser de mayor calidad que el de edificación, para garantizar una mayor homogeneidad y una ganancia temprana de resistencia que soporte las solicitaciones repetidas del tráfico pesado.
Burbujas de aire: el ingenioso sistema «anticongelante» interno
Puede resultar contraintuitivo, pero ¿por qué añadir «vacío» al hormigón para hacerlo más fuerte? En zonas con climas severos, es obligatorio utilizar aditivos aireantes para crear una red de microburbujas que actúan como «cámaras de expansión». Cuando el agua se filtra y se congela, aumenta su volumen. Sin estos poros, la presión interna reventaría la matriz del hormigón. La normativa exige una proporción de aire ocluido entre el 4,5 % y el 6 % en volumen.
Pero este aire no solo protege del hielo. Desde el punto de vista de la ejecución, estos aditivos mejoran la trabajabilidad y la tixotropía de un hormigón que debe tener una consistencia «seco-plástica» (con un asentamiento en el cono de Abrams de entre 2 y 6 cm). Esta baja fluidez es esencial para evitar la «caída de los bordes» del pavimento recién vertido al utilizar equipos de encofrado deslizante y así mantener la geometría perfecta de la calzada.
La carrera contra el reloj: el umbral crítico de las 24 horas
Una carretera de hormigón no es una pieza única, sino un conjunto de losas que deben poder contraerse y expandirse. Si no se le indica al hormigón por dónde debe romperse, lo hará de forma descontrolada. Aquí es donde el aserrado de juntas se convierte en una operación quirúrgica. Según el Pliego de Prescripciones PG-3, el cronómetro es implacable:
Juntas transversales: deben serrarse dentro de las primeras 24 horas posteriores a la puesta en obra.
Juntas longitudinales: el plazo se extiende entre 24 y 72 horas.
La precisión técnica también determina la profundidad del corte: debe ser de 1/3 del espesor en las juntas longitudinales y de 1/4 del espesor en las transversales. Si el serrado se realiza muy pronto, los bordes se desportillan; si se hace demasiado tarde, la carretera ya habrá fisurado de forma irregular.
El «efecto bombeo»: el enemigo invisible bajo la losa
El fallo de una carretera de hormigón suele empezar por debajo de la superficie. El fenómeno conocido como bombeo o pumping de finos se produce cuando coinciden el tráfico pesado, el agua acumulada y una base con exceso de partículas finas (es decir, aquellas que pasan por el tamiz de 0,063 mm). Bajo la presión del tráfico, la losa expulsa violentamente el agua mezclada con estos finos, descalzando el soporte de la carretera.
Para prevenirlo, la ingeniería limita estrictamente la masa unitaria de partículas cernidas por el tamiz de 0,125 mm (incluido el cemento) a un máximo de 450 kg/m³. En categorías de tráfico pesado, no basta con una base granular; es obligatorio el uso de bases de gravacemento. Este material, tratado con ligantes, proporciona un soporte uniforme e impermeable que resiste la erosión y evita que la losa quede «en el aire».
Pasadores y barras de unión: el secreto del movimiento coordinado
Para evitar que las losas se escalonen con el paso del tráfico, se recurre a la transferencia de carga. Esta transferencia de carga puede lograrse mediante la trabazón de áridos (el entrelazamiento natural en la fisura bajo la junta) o, de forma más robusta, mediante pasadores.
Los pasadores son barras de acero lisas que se colocan en las juntas transversales. Su elegancia radica en que permiten que la carretera «respire» (movimiento horizontal debido a las variaciones de temperatura) mientras transfieren la carga vertical de una losa a la siguiente. Así se reducen drásticamente las tensiones, se evita el bombeo y se previene la rotura de las esquinas. Además, las barras de unión mantienen las losas vinculadas lateralmente, lo que asegura la integridad estructural del conjunto.
Conclusión
Lo que percibimos como una simple cinta gris es, en realidad, un organismo técnico altamente sofisticado. Su excelencia reside en detalles que escapan al ojo inexperto, como una dosificación mínima de 300 kg/m³ de cemento (que asciende a 450 kg/m³ en la capa superior de pavimentos bicapa) y una relación agua/cemento que nunca debe superar el 0,46.
La próxima vez que circule por una autopista, recuerde que su seguridad depende de que el árido grueso tenga un coeficiente de Los Ángeles inferior a 35 y, sobre todo, de que la superficie mantenga un coeficiente de pulimento acelerado (CPA) no inferior a 0,50. La ingeniería de pavimentos es, en última instancia, el arte de controlar lo invisible para garantizar la estabilidad de cada kilómetro de nuestro viaje.
En esta conversación puedes escuchar las ideas más interesantes sobre los pavimentos rígidos utilizados en las carreteras.
Este vídeo resume los conceptos básicos de este tipo de pavimentos.
YEPES, V. (2026). Fabricación y puesta en obra del hormigón. Colección Manual de Referencia, serie Ingeniería Civil. Editorial Universitat Politècnica de València, 450 pp. Ref. 441. ISBN: 978-84-1396-418-8
El vertido del hormigón no marca simplemente el final del transporte, sino que constituye el «momento de la verdad» en cualquier proyecto de construcción. En este momento se determinan la integridad, la durabilidad y la vida útil de la estructura. Un error en la puesta en obra puede convertir un material de alta calidad y alto coste en una estructura con fallos invisibles que comprometerán su resistencia en las próximas décadas.
Debemos entender que el hormigón fresco es un material sensible que requiere disciplina. La forma en que llega al encofrado determinará si se mantendrá su homogeneidad o si aparecerán patologías evitables. A continuación, desglosamos las prácticas técnicas esenciales que marcan la diferencia entre una ejecución mediocre y otra excelente desde el punto de vista estructural.
La regla de oro de los dos metros (la gravedad, enemiga).
Uno de los errores más comunes en obra es permitir que el hormigón caiga desde alturas excesivas por comodidad. Sin embargo, la gravedad puede disgregar la mezcla. El vertido siempre debe realizarse en dirección vertical y lo más cerca posible de su posición definitiva. Si se superan los dos metros de caída libre, se produce la segregación de la masa y pueden producirse daños por impacto en los encofrados, así como desplazamientos en las armaduras y en los conductos de pretensado.
Para evitar que el material choque y rebote contra el acero, es imperativo utilizar «tubos de caída flexible» o «tubos centrales» que encaucen el flujo. Si se opta por el uso de láminas de plástico flexible (faldones) para dirigir la masa, hay un detalle técnico vital: no se debe permitir que el faldón se sumerja más de 500 mm en el hormigón fresco, para facilitar su extracción y evitar que quede atrapado.
«El vertido desde alturas superiores a dos metros provoca necesariamente la disgregación de la masa de hormigón y puede ocasionar daños en los encofrados, así como desplazamientos de estos, de las armaduras y de los conductos de pretensado».
El arte de caminar hacia atrás: el secreto de las losas.
En el hormigonado de superficies horizontales, la técnica del operario es fundamental. La recomendación de oro es el «vertido en retroceso». Aunque resulte incómodo para el trabajador, consiste en avanzar vertiendo hormigón sobre la masa ya colocada.
¿Cuál es el secreto técnico que hay detrás? Al verter sobre el hormigón ya existente, el material nuevo solo atraviesa una capa, lo que garantiza una mayor homogeneidad. Además, la masa ya colocada amortigua la viscosidad del nuevo material y facilita su compactación natural. Este método garantiza que el frente de hormigonado avance abarcando todo el espesor de la capa y evita los desplazamientos horizontales incontrolados que separarían el árido del mortero.
El peligro silencioso de las «juntas frías» y el uso del vibrador.
Una junta fría se produce cuando una capa (tongada) comienza a fraguar antes de recibir la siguiente, lo que genera una unión débil. Para evitarlo, el ritmo de vertido debe ser uniforme y estar coordinado con los medios disponibles. La clave está en el correcto «cosido» de las capas, que deben tener un espesor entre 20 y 70 cm.
En este caso, la regla de campo es innegociable: el espesor de la capa debe ser siempre inferior a la longitud de la cabeza del vibrador. Solo así se garantiza que el equipo atraviese todo el espesor de la capa nueva y penetre en la anterior para consolidarlas. Como advertencia final, queda terminantemente prohibido utilizar el vibrador para «arrastrar» o distribuir el hormigón horizontalmente, ya que esta práctica es la principal causa de la disgregación de los elementos lineales.
Desafiando la pendiente: de abajo hacia arriba.
El hormigonado en superficies inclinadas plantea un reto físico: la tendencia del hormigón a deslizarse y la segregación debida a las distintas velocidades de los áridos. Existe una paradoja: el vibrado es indispensable para compactar, pero también es el principal motor del deslizamiento.
La orden técnica es hormigonar siempre de abajo hacia arriba. Por ello, debemos calcular el volumen y la distancia del vertido de modo que el hormigón ocupe su lugar tras un vibrado breve. Este control del tiempo de vibración, sumado al uso de elementos que encaucen el flujo (como tolvas o embudos), es lo único que garantiza que la masa no se desplace por la ladera y que se mantenga la estabilidad de la sección.
Cómo corregir un «nido de grava» (desde la descarga hasta la pala).
La calidad se controla desde el principio. Para evitar segregaciones iniciales, se recomienda utilizar una «cacera» (recipiente auxiliar) al vaciar la hormigonera, lo que reduce los riesgos antes de que el material llegue a la obra. Si, a pesar de esto, se detecta una zona con exceso de árido grueso (coquera o nido de grava), la corrección debe ser técnica; está prohibido intentar «tapar» el problema añadiendo mortero o hormigón blando encima.
El método correcto consiste en recoger las partículas de grava sobrantes con una pala y distribuirlas en «zonas blandas» (con exceso de mortero). Una vez redistribuido el árido, es obligatorio realizar un vibrado o un apisonado enérgico en la zona para reintegrar los componentes. Si no se realiza esta compactación final, la corrección será solo estética y no tendrá valor estructural.
«No se admitirá, bajo ninguna circunstancia, la puesta en obra de masas de hormigón que presenten indicios de inicio del fraguado, ya que ello compromete gravemente sus propiedades mecánicas y su correcta compactación».
Conclusión.
La puesta en obra es un proceso que exige disciplina técnica y supervisión constante. No se debe iniciar ningún vertido sin la conformidad expresa de la dirección facultativa, que debe verificar la correcta disposición de las armaduras y la estabilidad de los encofrados.
Al final de la jornada, debemos reflexionar: ¿compensa acelerar la construcción a costa de comprometer la durabilidad de una estructura diseñada para durar un siglo? El hormigón es un material noble, pero no perdona los errores una vez endurecido. Nuestra responsabilidad técnica es garantizar que ese «momento de la verdad» se lleve a cabo con la precisión que exigen la ingeniería y la seguridad pública.
Os he grabado un vídeo en el que explico este tipo de cuestiones de obra.
En esta conversación podrás escuchar consejos sobre cómo realizar un buen vertido de hormigón.
Este vídeo resume los conceptos clave de la colocación del hormigón.
ACI COMMITTEE 304. Guide for Measuring, Mixing, Transporting, and Placing Concrete. ACI 304R-00.
CALAVERA, J. et al. (2004). Ejecución y control de estructuras de hormigón. Intemac, Madrid, 937 pp.
FERNÁNDEZ CÁNOVAS, M. (2004). Hormigón. 7ª edición, Colegio de Ingenieros de Caminos, Canales y Puertos. Servicio de Publicaciones, Madrid, 663 pp.
GALABRU, P. (1964). Tratado de procedimientos generales de construcción. Obras de fábrica y metálicas. Editorial Reverté, Barcelona, 610 pp.
TIKTIN, J. (1994). Procesamiento de áridos: instalaciones y puesta en obra de hormigón. Universidad Politécnica de Madrid. Escuela Técnica Superior de Ingenieros de Caminos, Canales y Puertos. Madrid, 360 pp. ISBN: 84-7493-205-X.
YEPES, V. (2026). Fabricación y puesta en obra del hormigón. Colección Manual de Referencia, serie Ingeniería Civil. Editorial Universitat Politècnica de València, 450 pp. Ref. 441. ISBN: 978-84-1396-418-8
Es una estampa habitual en nuestras ciudades: un camión con un enorme tambor giratorio que avanza con parsimonia hacia una obra. Para la mayoría, no es más que un vehículo pesado de transporte. Sin embargo, bajo esa apariencia ruda se esconde un laboratorio rodante. Desde el punto de vista de la ingeniería civil, estos vehículos no son solo camiones, sino fábricas químicas en movimiento diseñadas para que el material más utilizado del mundo, el hormigón, llegue con las propiedades exactas necesarias para sostener nuestros puentes y edificios.
A continuación, te revelo los secretos técnicos que convierten a estos gigantes en piezas maestras de la logística constructiva.
El secreto de la capacidad variable: ¿agitador o mezclador?
Muchos ignoran que la capacidad de carga de un camión hormigonera no es fija, sino que depende de su función. El camión puede funcionar como agitador o como mezclador, y en cada caso la carga útil permitida varía.
Como mezcladora, recibe los componentes secos y el agua de amasado directamente en la central de dosificación. Durante el trayecto, el camión debe realizar el amasado completo. En este caso, su capacidad es menor (por ejemplo, 6,6 m³), ya que se requiere espacio libre en la cuba para que los materiales choquen, caigan y se integren perfectamente.
Como agitador, recibe el hormigón ya amasado en planta. Su única función es mantenerlo fluido y evitar la segregación. En este caso, puede aprovechar mucho mejor su volumen y alcanzar capacidades de hasta 8 m³.
No obstante, cuando hablamos de hormigón estructural, hay que tener en cuenta algo fundamental: el Código Estructural prohíbe expresamente la adición de agua (o cualquier otra sustancia) a la masa de hormigón una vez que sale de la planta, con las cantidades exactas de cada componente, que quedan registradas en el albarán de suministro (contenido de cemento, relación agua/cemento, etc.).
El ingenio de Arquímedes y la anatomía del tambor.
El movimiento del hormigón en la cuba no es aleatorio. La «magia» ocurre gracias a dos hileras de espirales helicoidales soldadas entre sí, que operan según el principio del tornillo de Arquímedes.
Físicamente, la cuba es una estructura cilíndrica cónica fabricada en chapa de alta resistencia al desgaste y montada con una inclinación de 15°. Para soportar las enormes fuerzas de torsión y el peso del material, el tambor descansa sobre un preciso sistema de ingeniería: una banda zunchada en la parte superior que se apoya en dos robustos rodillos y un eje inferior que gira sobre cojinetes de alta capacidad de carga. Gracias a este diseño, basta con cambiar el sentido de rotación para que el camión pase de amasar el material en el fondo a elevarlo mecánicamente hacia la tolva de descarga.
Detalle de las espiras de un camión hormigonera
La danza de las revoluciones: el ritmo exacto del hormigón.
El control de la mezcla se realiza mediante el embrague de la cabina. El conductor debe gestionar tres ritmos críticos de rotación, cada uno con un propósito específico para garantizar la integridad del material:
Carga y amasado (aproximadamente de 16 a 22 rpm): se utiliza la velocidad más alta (segunda velocidad) para integrar los componentes con rapidez tras la carga o para realizar el amasado final en la obra.
Transporte y agitación (aproximadamente de 1 a 6 rpm): según el modelo y el manual de operación, se utiliza una velocidad lenta para mantener el hormigón en movimiento constante y evitar que se segregue o que comience el fraguado prematuramente.
Descarga (7-10 rpm): velocidad intermedia que, al invertir el sentido de giro, garantiza un flujo constante y controlado del material hacia la canaleta de distribución.
Conviene recordar que estos valores son orientativos y pueden variar según el fabricante y el modelo del camión.
La carrera contrarreloj: la regla de los 90 minutos.
El transporte de hormigón es una lucha térmica y química.
El fraguado, entendido como el inicio del endurecimiento, no espera a nadie: en climas cálidos puede comenzar antes que en invierno, por lo que el tiempo de transporte y colocación debe controlarse con rigor.
No debe afirmarse que, cuando las distancias son largas, se añade agua al final del trayecto. El Código Estructural prohíbe expresamente añadir agua al hormigón una vez que ha salido de la planta. El depósito de agua del camión se destina principalmente a la limpieza y al lavado de los restos de hormigón al finalizar la descarga.
. La normativa es tajante al respecto:
«El Código Estructural recomienda que, en condiciones normales, el intervalo de tiempo entre la adición de agua de amasado al cemento y a los áridos y la colocación del hormigón no exceda de una hora y media (90 minutos).»
El corazón independiente: un seguro de vida contra el fraguado.
El mayor temor de un operario es que el hormigón se fragüe en la cuba por una avería del vehículo. En ese caso, la cuba se convertiría en una roca inservible de varias toneladas. Para evitar este desastre económico, la ingeniería ofrece dos sistemas de motorización con ventajas diferentes:
Motor auxiliar independiente: un motor diésel dedicado exclusivamente a hacer girar la cuba.
Ventaja: permite que la hormigonera siga operando aunque el camión sufra una avería, lo que ayuda a evitar que el hormigón pierda su trabajabilidad.
Ventaja: aumenta la vida útil del motor principal del vehículo.
Toma de fuerza: utiliza el motor del camión para accionar el tambor.
Ventaja: reduce el consumo de combustible al emplear un único motor.
Desventaja: requiere camiones con mayor potencia y una transmisión adecuada para el funcionamiento de la cuba.
Conclusión: la ingeniería que sostiene nuestras ciudades.
La próxima vez que veas un camión hormigonera, ya no lo verás como un simple vehículo pesado. Estarás ante una fábrica de alta precisión que combina la geometría milenaria de Arquímedes con las normativas vigentes en materia de seguridad química. Desde la chapa resistente al desgaste de su cuba hasta el control preciso de sus revoluciones, cada detalle está diseñado para garantizar que el hormigón de nuestros cimientos sea perfecto.
¿Volverás a mirar estos gigantes de acero de la misma forma ahora que conoces la física y la química que tienen lugar en su interior?
Os he grabado un vídeo del camión hormigonera. Espero que os guste.
En este audio podrás escuchar una conversación sobre el funcionamiento de esta máquina.
En este vídeo se recogen las ideas básicas sobre los camiones hormigonera.
YEPES, V. (2026). Fabricación y puesta en obra del hormigón. Colección Manual de Referencia, serie Ingeniería Civil. Editorial Universitat Politècnica de València, 450 pp. Ref. 441. ISBN: 978-84-1396-418-8
En el corazón de cualquier obra de infraestructura existe un componente cuya coreografía mecánica suele pasar desapercibida: la hormigonera. Mientras que los modelos basculantes convencionales dependen de una aparatosa inclinación para vaciar su contenido, las hormigoneras de eje horizontal ejecutan un sofisticado «baile de acero» en el que el tambor nunca cambia de ángulo. El espectáculo comienza con el skip, un cucharón de carga que trepa por guías inclinadas, impulsado por un torno eléctrico que acciona una máquina que, mediante un ingenioso diseño electromecánico, puede mezclar y descargar simplemente cambiando el sentido de su rotación. Esta capacidad no solo es una curiosidad técnica, sino también la clave para producir hormigón de alta calidad en grandes cantidades.
El giro inesperado: un tambor, dos destinos.
El secreto de estas máquinas reside en la «inversión de marcha». En lugar de inclinar una cuba que puede pesar varias toneladas, el sistema simplemente invierte el sentido de giro del motor. Esta solución es mucho más eficiente y económica desde el punto de vista mecánico para grandes volúmenes: mover 9 m³ de hormigón mediante un sistema basculante requeriría una fuerza hidráulica y un refuerzo estructural considerables, mientras que invertir la rotación es una tarea puramente eléctrica o de transmisión.
Este proceso es posible gracias a una arquitectura interna de palas helicoidales fijas. Según la documentación técnica de Rebut:
«Un conjunto eleva el hormigón hacia el centro durante la mezcla y el otro lo empuja hacia la abertura durante la descarga. Las palas están dispuestas en espiral para garantizar una mezcla uniforme y una descarga eficiente».
Las mezcladoras reversibles de sitio suelen manejar lotes de hasta 1 m³, mientras que las unidades industriales de tambor «no inclinable» alcanzan dimensiones cilíndrico-cónicas capaces de gestionar hasta 9 m³ y cuentan con tiempos de mezcla de apenas 40 segundos.
¿Por qué el primer amasado es «el sacrificio» necesario?
Como ingeniero, siempre tengo presente que la precisión del equipo no anula las leyes de la física. Un fenómeno inevitable es la adherencia: parte del mortero de la mezcla se queda pegada a las paredes metálicas de la cuba limpia. Por este motivo, la primera mezcla de la jornada suele ser menos homogénea y de peor calidad.
La recomendación técnica es realizar una «ligera amasada de mortero» antes de comenzar la producción. Este procedimiento no supone un desperdicio, sino una preparación necesaria: el mortero recubre las paredes, «enciende» la máquina y garantiza que, desde el primer lote de hormigón estructural, la dosificación de cemento y finos sea exactamente la que dicta el diseño de la mezcla.
La formulación matemática para un buen hormigón
El éxito de estas máquinas no es azaroso, sino que responde a fórmulas que relacionan la geometría del tambor con la física del amasado. Para obtener un hormigón homogéneo, el tiempo y la velocidad deben ajustarse al diámetro D de la cuba (medido en metros).
Dentro del tambor, operamos bajo dos reglas de oro:
El tiempo mínimo de amasado (en segundos) se calcula como t = 90 √D.
La velocidad de giro ideal (en revoluciones por minuto) se determina mediante la fórmula: N = 20 / √D.
Estas fórmulas garantizan que el material sea impulsado hacia el centro de la cuba con la energía necesaria para mezclarse sin que la fuerza centrífuga separe los componentes.
Silencio y durabilidad: el fin del contacto metal-metal.
Uno de los avances más significativos en la durabilidad de estas máquinas ha sido el rediseño de sus sistemas de arrastre y de soporte. Tradicionalmente, el contacto entre piñones y coronas provocaba un ruido ensordecedor y un desgaste acelerado. El diseño moderno ofrece dos soluciones:
Sistema de corona y piñón: un grupo motorreductor actúa sobre una corona dentada que rodea la cuba.
Sistema de fricción: aquí reside la verdadera innovación. El tambor se arrastra mediante rodillos con bandaje de goma o de poliuretano.
El uso de estos rodillos elásticos no solo reduce drásticamente el ruido operativo en la obra, sino que también actúa como un amortiguador que protege la estructura y minimiza el mantenimiento, incluso en máquinas con producciones masivas.
El desafío de la lentitud: el riesgo de la segregación.
A pesar de su sofisticación, el eje horizontal tiene un punto débil físico: la descarga tiende a ser lenta. Esto ocurre porque el material debe ser «empujado» hacia fuera por las palas en lugar de caer por la fuerza de la gravedad. Si la velocidad de giro (N) disminuye o si la mezcla contiene áridos de gran tamaño, puede producirse segregación: el mortero sale primero y los áridos gruesos quedan al final.
Consejo a pie de obra: el operador debe mantener una vigilancia constante durante la fase final del vaciado. Si se observa que el hormigón empieza a salir «descarnado» (solo piedra), hay que detener la descarga y realizar un breve remezclado en sentido de amasado para reincorporar los finos antes de terminar el vertido.
Conclusión: hacia una construcción de alta resistencia.
Las hormigoneras de inversión de marcha son auténticas bestias de carga, capaces de alcanzar producciones de 250 m³/h y capacidades de entre 5 y 9 m³. Su superioridad frente a los modelos basculantes en proyectos de gran envergadura es indiscutible, ya que ofrecen una mayor eficiencia mecánica y una mejor calidad de la mezcla.
No obstante, la ingeniería no se detiene. Para proyectos de hormigón masivo o de ultra alta resistencia, la industria ya empieza a decantarse por los sistemas de doble eje. ¿Será suficiente la optimización del tambor reversible para afrontar los retos del futuro o estamos llegando al límite físico de lo que un solo eje horizontal puede lograr?
Os he grabado un vídeo sobre esta máquina. Espero que os guste.
En esta conversación puedes escuchar las ideas más interesantes sobre el funcionamiento de esta máquina.
En este vídeo se resumen bien los principios fundamentales de esta hormigonera.
ACI COMMITTEE 304. Guide for Measuring, Mixing, Transporting, and Placing Concrete. ACI 304R-00.
FERNÁNDEZ CÁNOVAS, M. (2004). Hormigón. 7ª edición, Colegio de Ingenieros de Caminos, Canales y Puertos. Servicio de Publicaciones, Madrid, 663 pp.
CORMON, P. (1979). Fabricación del hormigón. Editores Técnicos Asociados, Barcelona, 232 pp.
GALABRU, P. (1964). Tratado de procedimientos generales de construcción. Obras de fábrica y metálicas. Editorial Reverté, Barcelona, 610 pp.
TIKTIN, J. (1994). Procesamiento de áridos: instalaciones y puesta en obra de hormigón. Universidad Politécnica de Madrid. Escuela Técnica Superior de Ingenieros de Caminos, Canales y Puertos. Madrid, 360 pp. ISBN: 84-7493-205-X.
YEPES, V. (2026). Fabricación y puesta en obra del hormigón. Colección Manual de Referencia, serie Ingeniería Civil. Editorial Universitat Politècnica de València, 450 pp. Ref. 441. ISBN: 978-84-1396-418-8
El sector del cemento y el hormigón pretende alcanzar la neutralidad en emisiones de carbono para el año 2050 integrando principios de economía circular en todas sus etapas productivas. Este cambio de paradigma, impulsado por la Global Cement and Concrete Association, propone sustituir el modelo lineal tradicional por estrategias que priorizan la reducción, la reutilización y el reciclaje de materiales.
Entre las acciones clave se encuentran el uso de combustibles alternativos en hornos de clínker, la incorporación de residuos industriales en las mezclas y el diseño de estructuras desmontables. Además, el sector apuesta por la innovación tecnológica para optimizar la capacidad natural del hormigón para absorber CO2 y prolongar la vida útil de las construcciones. El éxito de esta transición requiere una estrecha colaboración entre los sectores público y privado para establecer normativas que fomenten la sostenibilidad y la gestión eficiente de los recursos.
El desafío de los 100 mil millones de toneladas.
Según el Foro Económico Mundial, cada año la economía mundial consume la abrumadora cantidad de 100 mil millones de toneladas de materiales. Lo más alarmante es que cerca de la mitad de estos recursos se destinan exclusivamente a la ingeniería y la construcción.
Con una proyección de 2000 millones de nuevos hogares para el año 2100, el modelo lineal de «tomar-hacer-desechar» resulta físicamente inviable. La economía circular ya no es una opción romántica, sino el pilar técnico indispensable para alcanzar la neutralidad de emisiones de carbono en 2050.
Más allá del reciclaje: las «9R» en el mundo del cemento.
Para transformar este sector, debemos comprender tres estrategias fundamentales: cerrar ciclos (utilizar residuos como la escoria de alto horno), estrechar ciclos (optimizar el uso de áridos reciclados) y ralentizar ciclos (extender la vida útil).
El Programa de Naciones Unidas para el Medio Ambiente (PNUMA) propone las «9R», que en la industria del hormigón se adaptan a estas seis categorías críticas:
Reducir por diseño: disminuir el uso de material virgen en la ingeniería.
Reciclar: procesar el hormigón al final de su vida útil para producir áridos reciclados de calidad controlada.
Readaptar: colocar en el mercado elementos que cumplan una función igual o mejor que la de uno nuevo.
Reutilizar: mantener los componentes en uso siempre que sea posible.
Rechazar y reducir: usar menos artículos y prolongar su vida útil.
Reparar, renovar y remanufacturar: mantener lo existente en lugar de demoler y reemplazar.
La durabilidad extrema del hormigón es su mayor activo circular. Su resistencia innata a incendios, inundaciones y condiciones meteorológicas adversas hace que las estructuras permanezcan útiles durante décadas con un mantenimiento mínimo.
El hormigón como «esponja» de CO2: el fenómeno de la recarbonatación.
La recarbonatación es un proceso natural disruptivo en el que el hormigón absorbe CO₂ de la atmósfera. Este fenómeno convierte el material en un sumidero de carbono vivo. Un detalle técnico vital es que este proceso se maximiza tras la demolición, ya que aumenta la superficie expuesta del material.
Este cambio de paradigma permite reducir las emisiones de carbono en el entorno construido. Como señala la Global Cement and Concrete Association (GCCA) en su posicionamiento oficial:
«La adopción de la economía circular es uno de los elementos clave para alcanzar la neutralidad de emisiones de carbono en 2050, como se menciona en la hoja de ruta del organismo internacional».
Coprocesamiento: transformando residuos en energía y materia.
La industria emplea el coprocesamiento, una forma de simbiosis industrial que utiliza residuos como combustibles y materias primas alternativas (ARMs). El uso de neumáticos viejos en hornos de clínker es un caso de éxito emblemático.
Esta práctica soluciona el problema crítico que supone la gestión de residuos de combustión lenta y perjudicial y reduce la dependencia de los combustibles fósiles. Es una eficiencia pura: transformar los desechos de la sociedad en un recurso industrial de alto valor.
Diseño modular y desmontable: construir para el futuro.
La circularidad se define en la fase de proyecto. Actualmente, la innovación se divide en dos frentes:
Diseño de productos: Uso de materiales cementosos suplementarios, como las cenizas volantes, que optimizan la composición del hormigón y mejoran su resistencia.
Diseño de proyectos: Implementación de sistemas prefabricados y modulares.
El concepto de «diseñar para el desensamblaje» permite tratar los edificios completos como bancos de materiales. Las losas y los paneles prefabricados pueden desmontarse y reutilizarse en nuevas estructuras, lo que elimina de raíz la generación de escombros.
Un pacto por la transparencia y la innovación.
La GCCA y sus miembros se han comprometido a acelerar las métricas circulares y a fomentar la colaboración público-privada. No obstante, para ampliar estos resultados se necesitan marcos regulatorios valientes.
Una de las propuestas más urgentes es la eliminación gradual de los vertederos destinados a los residuos de construcción. Al prohibir el envío de escombros de hormigón a vertederos, se garantiza su reincorporación al ciclo productivo, de modo que cada tonelada de material mantenga su valor máximo.
Conclusión: ¿Estamos preparados para dejar atrás la era del desperdicio?
La transición hacia la economía circular supone un cambio de paradigma que genera valor, resiliencia y eficiencia operativa. Al integrar la recarbonatación, el coprocesamiento con ARMs y el diseño desmontable, la industria está redefiniendo el concepto de construcción.
El fin de la era del desperdicio no es solo una meta medioambiental, sino también una realidad técnica en curso. Ante este avance, la pregunta es inevitable: ¿Seguiremos viendo al hormigón como un material inerte o lo reconoceremos finalmente como la infraestructura que nos protegerá en 2050?
En esta conversación puedes escuchar los aspectos más importantes de la revolución circular del hormigón.
En este vídeo se resumen bien las ideas más interesantes sobre este tema.
Nuestras ciudades crecen a un ritmo vertiginoso, pero este progreso esconde una crisis climática silenciosa en sus cimientos. Según el reciente informe Global Status Report for Buildings and Construction 2024/2025, el sector de la edificación es responsable del 32 % del consumo mundial de energía y del alarmante 34 % de las emisiones de CO₂. En este contexto, el acero y el cemento se perfilan como los principales responsables, ya que representan por sí solos el 18 % de la huella de carbono total del sector.
Ante la urgencia climática, la ingeniería estructural se enfrenta a un desafío técnico fascinante: ¿podemos diseñar edificios más ligeros y sostenibles sin comprometer la seguridad estructural? Y, más específicamente, ¿cómo podemos romper el «paradigma del catálogo» cuando las soluciones comerciales estándar alcanzan sus límites físicos y medioambientales?
Al final de este post, en la referencia, tienes un enlace directo para descargar gratuitamente el artículo científico completo, ya que está publicado en abierto.
El poder de la optimización: Rompiendo los límites del catálogo
Las vigas alveolares son perfiles de acero con aberturas circulares en su interior que permiten aumentar la altura de la viga y, por tanto, su eficiencia, sin añadir masa. Sin embargo, la práctica tradicional se ha limitado a replicar soluciones de los catálogos de los fabricantes, que suelen ser restrictivos.
Un hallazgo clave del estudio paramétrico actual revela que, para luces de 4 metros, los catálogos a menudo alcanzan su límite máximo permitido y dejan de ofrecer soluciones factibles bajo cargas elevadas. La verdadera innovación surge al dejar de considerar la losa colaborante como un elemento estático de catálogo. Al tratar variables como el espesor de la chapa y, sobre todo, la tasa de refuerzo de la losa como componentes activos del diseño, la ingeniería supera las barreras de los fabricantes tradicionales.
Algoritmos que imitan a la naturaleza: El «Particle Swarm Optimization» (PSO)
Para navegar por este complejo mar de posibilidades, se ha recurrido a la inteligencia colectiva del algoritmo de optimización por enjambre de partículas (PSO). No se trata de un simple ejercicio de búsqueda, sino de resolver un problema de objetivo único, restringido y con variables discretas.
El algoritmo funciona como un enjambre que explora un amplio espacio de búsqueda (identificado en la tabla 1 del estudio), evaluando simultáneamente 201 perfiles de acero diferentes, diversas resistencias de hormigón y geometrías de alvéolos, con el objetivo de encontrar la configuración que genere la menor huella de carbono posible.
«El algoritmo PSO ha demostrado ser eficaz para identificar soluciones óptimas, ya que permite que la introducción de refuerzo en la losa, combinada con un diseño optimizado, genere un impacto significativo en el diseño estructural».
El dato impactante: una reducción del 25% en emisiones de CO2
La precisión algorítmica no es solo un alarde tecnológico, sino que se traduce en un impacto medioambiental significativo. El análisis paramétrico demuestra que, especialmente en niveles de carga altos (6 kN/m²) y luces de gran tamaño, la optimización integrada del sistema viga-losa puede reducir las emisiones de CO₂ hasta un 25 %.
Este logro ecológico no se debe a un solo cambio, sino a una redistribución holística de los materiales. Al añadir refuerzo estratégico en la losa, el sistema permite reducir simultáneamente el espesor del steel deck y el volumen de hormigón superior, lo que disminuye directamente la masa de los materiales base que más contribuyen al calentamiento global.
Análisis de materiales: Por qué lo «más fuerte» no siempre es «más verde»
Es fundamental desmitificar la idea de que los materiales de alta resistencia siempre son la mejor opción sostenible. Al analizar las soluciones óptimas, los «ganadores» constantes fueron:
Acero: ASTM A572 Gr. 50 (con un factor de emisión de CO2 de 2.04 kgCO2/kg).
Hormigón: 25 MPa (con un factor de emisión de 374,00 kg de CO2/m³).
La clave del diseño inteligente radica en que estos materiales presentan factores de emisión inferiores a los de sus equivalentes de alta resistencia. Por ejemplo, el acero A913 Gr. 65 tiene una mayor huella de carbono (2,13 kg CO2/kg) que el A572 Gr. 50. Por tanto, la eficiencia no depende de la potencia bruta del material, sino de una combinación inteligente y precisa dictada por el algoritmo.
Desmitificando el proceso: el peso de la masa frente al fuego industrial
A menudo se cuestiona si el proceso de fabricación de una viga con agujeros (corte y soldadura) compensa el ahorro de material. Los datos del estudio son contundentes y desmienten este mito:
Corte y soldadura insignificantes: Estos procesos industriales representan habitualmente menos del 1% de las emisiones totales de la estructura.
El dominio de la masa: El factor crítico sigue siendo la masa del perfil de acero original, que puede representar hasta el 70% del CO2 en escenarios optimizados.
El papel de la losa: El steel deck tiene un impacto considerable, oscilando entre el 11% y el 39% de las emisiones totales según la luz de la estructura.
En definitiva, el «coste» ambiental de perforar la viga es un precio mínimo frente al gran ahorro de material que permite su nueva geometría.
Conclusión: Hacia una ingeniería de precisión ambiental
Estamos dejando atrás la era de la construcción basada en la sobreespecificación y en el uso de catálogos estáticos. El futuro es la Ingeniería de Precisión Ambiental, donde cada componente, desde el diámetro del alvéolo hasta el milímetro de refuerzo en la losa, se trata como una variable viva.
La inteligencia artificial y el diseño paramétrico nos proporcionan las herramientas necesarias para reducir en una cuarta parte la huella de carbono de nuestras estructuras. Ante la actual crisis climática, la pregunta para los diseñadores ya no es si estos métodos funcionan, sino: ¿podemos permitirnos seguir construyendo con los ojos cerrados y con los catálogos del siglo pasado? El diseño integrado es nuestra herramienta más poderosa para redefinir el impacto de nuestro entorno construido.
En esta conversación puedes escuchar un debate sobre estas ideas.
En este vídeo se resumen bien las ideas más interesantes.
Acaban de publicar un artículo en el Journal of Information Technology in Construction,una de las revistas ubicadas en el primer decil del JCR. Este documento sintetiza los hallazgos del desarrollo y la validación de Endurify 2.0, un sistema de programación automatizada basado en el Modelado de Información de Construcción (BIM) para el mantenimiento estructural.
Nuestro equipo ha centrado sus esfuerzos en el uso de modelos analíticos, el sistema evalúa la vida útil remanente de los elementos constructivos basándose en indicadores de degradación como la carbonatación y la fisuración. Los datos obtenidos se procesan mediante algoritmos de decisión multicriterio para generar planes de mantenimiento automatizados que equilibran la seguridad estructural con la eficiencia económica. Esta metodología busca reducir en un 15% los costes de intervención y mitigar el impacto social negativo sobre los residentes. La investigación se enmarca en el proyecto RESILIFE, que dirijo como investigador principal en la Universitat Politècnica de València. A continuación, se presenta un resumen del trabajo y de la información de contexto.
¿Puede un algoritmo predecir el «infarto» estructural de un edificio antes de que aparezca la primera fisura visible? Nuestro equipo ha desarrollado Endurify 2.0, una inteligencia clínica integrada en modelos 3D que convierte la experiencia de los expertos en una disciplina matemática exacta. Esta innovación no solo ahorra un 15 % en costes, sino que también utiliza el big data para decidir cuándo y cómo intervenir en un edificio para prolongar su vida útil en décadas, minimizando el trauma social que suponen las obras en las comunidades de vecinos.
Esta investigación ha sido dirigida por investigadores del Instituto de Ciencia y Tecnología del Hormigón (ICITECH) de la Universitat Politècnica de València (UPV). Su trabajo propone un cambio de paradigma: dejar de considerar los edificios como objetos estáticos y empezar a gestionarlos como organismos vivos cuyos «órganos» (vigas y pilares) envejecen a ritmos distintos debido a la acción constante de la química y la física.
La situación es urgente. La industria de la construcción consume el 50 % de los recursos extraídos en todo el mundo y es responsable del 35 % de las emisiones de gases de efecto invernadero. En España, el problema es estructural: más del 57 % de las viviendas se construyeron antes de 1980, en una época en la que las normativas sobre durabilidad casi no existían. Nos enfrentamos a millones de toneladas de hormigón que han superado su vida útil teórica de 50 años y requieren una intervención de rehabilitación, no de demolición, como exige la economía circular.
La pregunta de investigación: ¿Cómo optimizar el «corazón» del edificio?
El equipo de la UPV se planteó un reto ambicioso: ¿es posible automatizar la toma de decisiones en materia de rehabilitación para que sea más eficiente que la de un experto humano? El objetivo era crear una herramienta capaz de procesar la degradación invisible y generar planes de obra multietapa que equilibraran el ahorro económico con la comodidad de los residentes.
Metodología: Los cuatro «jinetes» de la degradación
Para crear Endurify 2.0, los investigadores integraron un motor de cálculo en Autodesk Revit® (el estándar de modelado BIM). La metodología analiza cada elemento estructural mediante cuatro indicadores críticos:
Fisuración transversal: las primeras heridas que aceleran el daño.
Carbonatación: un proceso químico que reduce la alcalinidad del hormigón, dejando las armaduras de acero indefensas frente a la corrosión (según el modelo de Tuitti).
Fluencia: la deformación silenciosa que sufre el hormigón bajo una carga sostenida a lo largo de los años.
Deflexión: pérdida de rigidez que compromete la seguridad y la percepción del usuario.
El sistema utiliza una «lógica del peor de los casos»: la vida útil remanente (RUL) de una viga se determina por el primer indicador que supera el umbral de seguridad. Una vez detectados los elementos de riesgo, el algoritmo TOPSIS (una técnica de decisión multicriterio) evalúa miles de combinaciones posibles para agrupar las reparaciones de manera lógica y eficiente desde el punto de vista espacial.
Resultados: Superando al ojo humano
La validación se realizó en un modelo de 191 vigas de hormigón armado. Los resultados son reveladores: en comparación con un plan de rehabilitación diseñado manualmente por un ingeniero experto, el sistema automatizado consiguió:
Reducir el coste total en un 15,16 %.
Disminuir el impacto social (proximidad de las obras a las viviendas) en un 10,46 %.
Optimizar la logística de obra, agrupando las intervenciones en fases que reducen la necesidad de montar y desmontar andamios o instalaciones de obra repetidamente.
Aplicabilidad: El semáforo de la salud estructural
La gran innovación de Endurify 2.0 es la persistencia de los datos. Al devolver los resultados al modelo BIM mediante «parámetros compartidos», cualquier gestor puede visualizar el edificio mediante un código de colores (como un semáforo) que indica qué piezas necesitan «cirugía» inmediata y cuáles pueden esperar. Esto permite a los propietarios de grandes carteras inmobiliarias planificar inversiones a 20 años con base científica, en lugar de recurrir a soluciones reactivas cuando el daño ya es crítico.
Conclusiones y el futuro: Hacia el «Gemelo Digital» total
El estudio concluye que la rehabilitación científica es la única forma de cumplir con el Pacto Verde Europeo y de transformar el mantenimiento en una estrategia proactiva.
Las futuras líneas de investigación se centran en la automatización total de la inspección mediante visión artificial y drones para alimentar el modelo BIM sin intervención humana, y en la integración de sensores en tiempo real para crear verdaderos gemelos digitales que avisen al móvil del gestor cuando una viga sufra un estrés inesperado. Con Endurify 2.0, el futuro de la arquitectura no consiste en construir más, sino en cuidar con inteligencia matemática lo que ya tenemos.
Como el artículo se ha publicado en abierto, os lo podéis descargar en el siguiente enlace:
¿Cómo es posible que una viga de hormigón, un material intrínsecamente frágil en lo que respecta a la tracción, soporte el paso de miles de vehículos en un viaducto sin colapsar ni agrietarse? La respuesta no radica en el grosor de la estructura, sino en un «secreto invisible»: la precompresión activa. Como ingenieros, no solo vertemos material, sino que diseñamos un estado de tensiones internas que permite a las infraestructuras modernas desafiar los límites de la física.
Aunque ya he escrito varios artículos sobre este tema en el blog, a continuación, se presentan las cinco claves técnicas que convierten el hormigón en una herramienta de ingeniería de alta precisión.
No se trata solo de soporte, sino de resistencia activa.
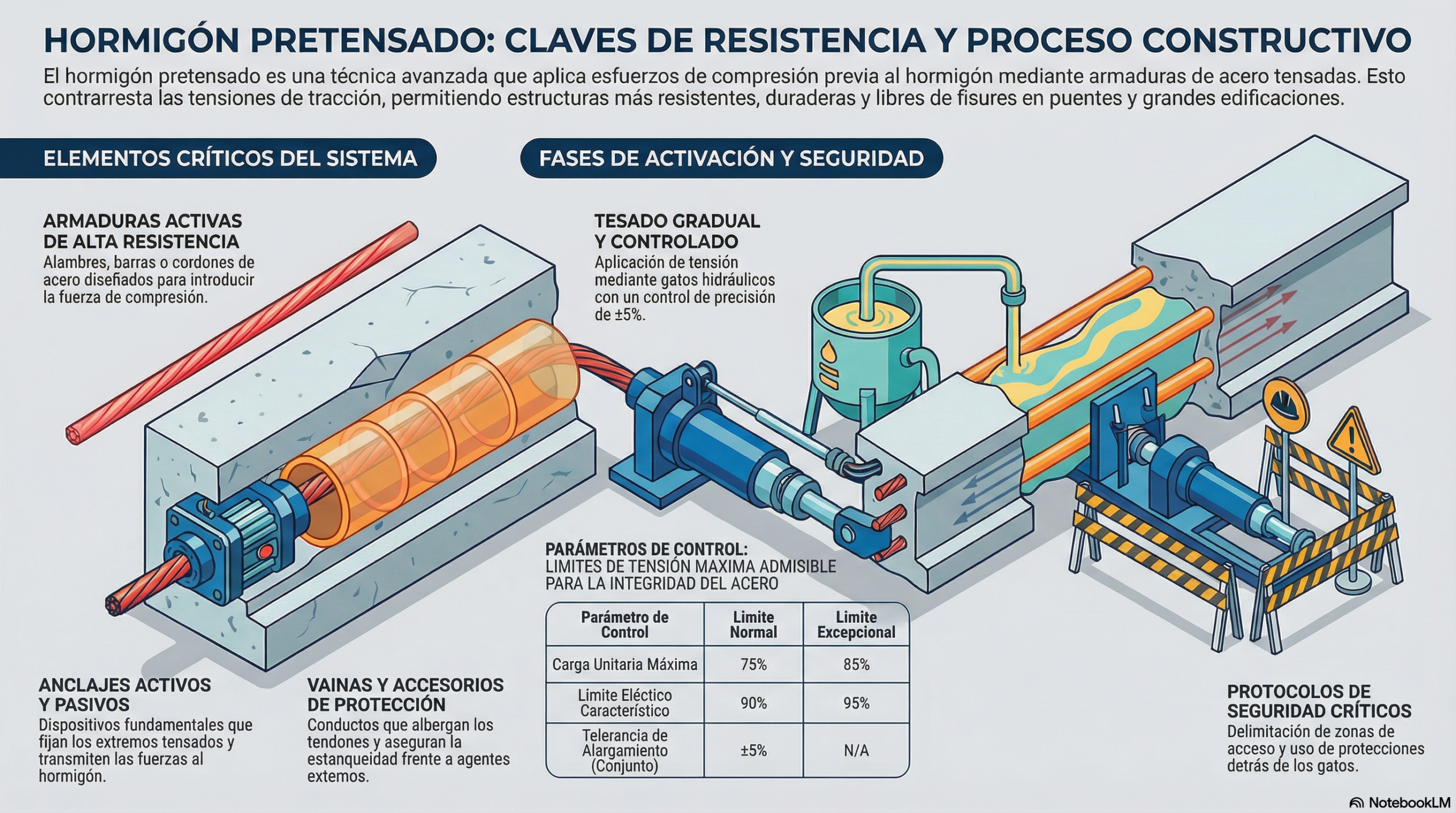
El cambio de paradigma fundamental es que el hormigón pretensado no «espera» a recibir la carga para trabajar. Mediante esta técnica, sometemos al material a un esfuerzo de compresión previo que contrarresta las tracciones que sufrirá durante su vida útil. Esto lo convierte en un sistema dinámico.
Para que esta «fuerza interna» sea efectiva, incluso el almacenamiento de los materiales se rige por estrictas normas de ingeniería. Por ejemplo, los alambres de alta resistencia no pueden enrollarse de cualquier manera: su diámetro de bobinado nunca debe ser inferior a 250 veces el diámetro del propio alambre, a fin de evitar deformaciones permanentes que puedan afectar su capacidad elástica. Como bien define la normativa técnica:
«El pretensado es una técnica que aumenta la capacidad de resistencia del hormigón a las cargas al someterlo previamente a esfuerzos de compresión».
El acero como un «músculo» en tensión.
Las denominadas armaduras activas son el alma de la estructura. No nos referimos al acero corrugado convencional, sino a elementos de alta resistencia que actúan como músculos sometidos a una tensión constante. En función del diseño, el ingeniero selecciona diferentes configuraciones:
Alambres: suministrados en rollos, son fundamentales para el control de la deformación.
Barras: se suministran en tramos rectos para garantizar su integridad y evitar daños durante el transporte.
Cordones: trenzados de dos, tres o siete alambres. Para garantizar su «fuerza vital», los cordones de dos o tres alambres requieren rollos de al menos 600 mm de diámetro, mientras que los de siete alambres exigen bobinas de 750 mm de diámetro.
Para evitar la corrosión y mantener la adherencia, estas armaduras deben guardarse en lugares ventilados, lejos de la humedad y libres de grasas o polvo, que podrían alterar la longitud de transmisión necesaria para transferir el esfuerzo al hormigón.
La coreografía de la precisión: gatos y anclajes.
El proceso de tensado es una coreografía lenta y progresiva en la que la fuerza bruta se gestiona con precisión milimétrica. Utilizamos gatos hidráulicos y centrales de presión para aplicar la carga sobre los anclajes, que se clasifican según su función: el anclaje activo (tipo L) se encuentra en el extremo de tensado, mientras que el anclaje pasivo (tipo S) en el extremo fijo.
En obra, la precisión no es negociable. La fuerza aplicada debe mantenerse dentro de un margen de ±5 % respecto al valor del proyecto. Controlamos los alargamientos con tolerancias muy estrictas: un máximo de ±15 % para un tendón individual, pero solo de ±5 % para el conjunto de tendones de la misma sección. Además, como ingenieros sénior, sabemos que el termómetro manda: está prohibido iniciar el tesado por debajo de 5 °C sin medidas especiales. Es una máxima del sector que
«Cualquier fallo en el tensado o en los materiales puede afectar a la integridad estructural del proyecto».
Vainas de inyección: mucho más que un relleno.
Las vainas no son simples tubos, sino conductos que garantizan la durabilidad. En los sistemas postensados, tras el tensado, inyectamos una lechada técnica que debe cumplir con estrictos parámetros químicos. Utilizamos cemento Portland CEM-I con una relación agua/cemento (a/c) entre 0,4 y 0,5 para garantizar una porosidad mínima y una protección óptima.
La inyección es un proceso crítico:
Velocidad y longitud: La lechada debe avanzar de forma constante entre 5 y 15 m/min, sin superar nunca una longitud de inyección de 120 m.
Control térmico: La temperatura de la mezcla jamás debe exceder los 30 °C para evitar fraguados prematuros dentro de la vaina.
Puntos de purga: El éxito se confirma en los respiraderos o tubos de purga. La operación solo termina cuando la lechada rebosa por ellos con la misma consistencia y densidad que la mezcla original.
La seguridad en entornos de altas energías.
Un tendón de pretensado que acumula tensión es, en esencia, un resorte gigante con una energía potencial letal. La seguridad no se reduce al sentido común, sino que implica un protocolo de «altas energías». Es obligatorio establecer un perímetro de seguridad estricto y utilizar placas perforadas o envoltorios que actúen como escudo en caso de que una armadura llegara a partirse.
Existen prohibiciones críticas por motivos de seguridad y técnicos: está terminantemente prohibido utilizar aire comprimido para la inyección y, bajo ningún concepto, los operarios deben mirar a través de los tubos o rebosaderos durante el proceso. La ingeniería moderna debe equilibrar una fuerza física inmensa con un control humano absoluto, documentando cada presión y cada alargamiento para garantizar la trazabilidad total de la estructura.
Conclusión: mirando al futuro de la ingeniería.
El hormigón pretensado es la victoria de la inteligencia sobre la debilidad intrínseca de los materiales. Al dominar la presión interna controlada, hemos pasado de construir estructuras pesadas y pasivas a diseñar obras de arte de la ingeniería que, en realidad, son organismos activos en equilibrio.
Al observar la esbeltez de un puente moderno, cabe preguntarse: ¿seremos capaces de diseñar estructuras aún más ligeras y atrevidas ahora que sabemos que la verdadera fuerza reside en la presión interna invisible que las sostiene?
En esta conversación puedes escuchar algunas de las claves del hormigón pretensado.
En este vídeo se resumen las ideas más interesantes de este material.
En este documento se describen las ideas fundamentales:
YEPES, V. (2026). Fabricación y puesta en obra del hormigón. Colección Manual de Referencia, serie Ingeniería Civil. Editorial Universitat Politècnica de València, 450 pp. Ref. 441. ISBN: 978-84-1396-418-8
Acaban de publicar un artículo nuestro en Sustainable Cities and Society, una de las revistas de mayor impacto científico, ubicada en el primer decil del JCR. En este trabajo se propone un enfoque integrador basado en el ciclo de vida y en métodos de evaluación multicriterio para analizar la vivienda social sostenible. La investigación se enmarca en el proyecto RESILIFE, que dirijo como investigador principal en la Universitat Politècnica de València. A continuación, se presenta un resumen del trabajo.
Los principales resultados revelan que el sistema Light Steel Frame (LSF) es la alternativa más sostenible, ya que logra un equilibrio superior entre la eficiencia en el uso de los recursos, la durabilidad y la reducción del mantenimiento. Un descubrimiento crucial es el papel de la dimensión social, que representó casi el 40 % del peso total en la evaluación, por encima de las dimensiones económica y medioambiental. El análisis causal identifica el coste de construcción, la funcionalidad y los agentes de la cadena de valor como los principales factores que condicionan el rendimiento sostenible del resto del sistema.
El artículo presenta un marco metodológico integrador que combina evaluaciones basadas en el ciclo de vida —análisis de ciclo de vida (LCA), análisis de coste del ciclo de vida (LCC) y análisis de ciclo de vida estocástico (S-LCA)— con técnicas avanzadas de decisión multicriterio: método mejor-peor (BWM), análisis DEMATEL difuso y análisis MARCOS. Esta integración permite incorporar ponderaciones de expertos, modelar relaciones causales entre criterios y sintetizar resultados frente a soluciones ideales o anti-ideales, lo que aumenta la transparencia en la priorización de alternativas constructivas. Este enfoque se ha aplicado a un caso real de vivienda social en Perú, en el que se han comparado cinco sistemas estructurales representativos: LSF, LBSPS, RCW, RCF-M y RCF-CP. El estudio ha proporcionado pruebas empíricas sobre los costes del ciclo de vida, los impactos ambientales y las prestaciones sociales que respaldan las decisiones de diseño y las políticas.
El estudio analiza cinco sistemas constructivos adaptados a contextos de urbanización rápida (específicamente en Lima, Perú), que van desde métodos convencionales hasta industrializados:
Entre las aportaciones metodológicas, la combinación de BWM con una agregación basada en credenciales profesionales reduce la carga de comparación y atenúa los sesgos en la agregación de juicios, mientras que la extensión difusa de DEMATEL permite identificar los criterios que funcionan como impulsores del sistema y los que actúan como receptores. Esta capacidad para distinguir entre causas y efectos permite aclarar qué palancas hay que modificar para lograr efectos amplificados en la sostenibilidad. Por último, la validación cruzada con otros métodos de MCDM y los ensayos de sensibilidad aumentan la confianza en la estabilidad de los resultados.
Discusión de resultados
Los análisis económicos muestran que, en un horizonte de 50 años y por metro cuadrado, los sistemas basados en acero ligero (LSF) tienen los menores costes totales de ciclo de vida, mientras que algunas alternativas prefabricadas, como el LBSPS, tienen los mayores costes de construcción. Estos datos implican que si solo se tiene en cuenta la inversión inicial, se pueden tomar decisiones subóptimas, ya que no se consideran el mantenimiento y el fin de vida.
En términos ambientales, la evaluación con ReCiPe (endpoint) sitúa al LSF como el sistema con el menor impacto agregado, principalmente debido a su menor intensidad material. Por el contrario, las soluciones con mayor presencia de hormigón y ladrillo presentan una carga superior, especialmente en la dimensión de recursos. Esta diferenciación pone de manifiesto la influencia del perfil material y del proceso de fabricación en la huella medioambiental de la vivienda y sugiere que, en la práctica profesional, se deben priorizar medidas que reduzcan la demanda de materiales energéticamente intensivos en la fase de fabricación.
La S-LCA revela una tensión entre la industrialización y la exposición social: las alternativas más industrializadas, como el LSF y el LBSPS, presentan mayores valores de exposición laboral y de funcionalidad exigente, mientras que las tipologías convencionales de hormigón muestran menores riesgos sociales, medidos en Medium Risk Hours. Este resultado indica que la adopción de sistemas industrializados exige prestar atención explícita a la gestión del trabajo, la formación y la coordinación de la cadena de suministro para evitar que los impactos negativos se transfieran al personal y a la comunidad.
La síntesis mediante MARCOS ubica a LSF como la alternativa mejor valorada en el escenario analizado, seguida de RCW y RCF-M. Los sistemas LBSPS y RCF-CP quedan en posiciones inferiores. Las pruebas de sensibilidad (variación de los pesos de ±15 %, escenarios de distancia de transporte y estratificación de expertos) muestran que el orden general se mantiene, lo que indica cierta robustez frente a perturbaciones razonables en los supuestos. Estos resultados permiten extraer una conclusión práctica: en contextos con características similares a las del caso estudiado, las soluciones ligeras industrializadas pueden mejorar la relación entre coste, impacto ambiental y rendimiento técnico, siempre que se gestionen adecuadamente los aspectos sociales y de ejecución.
Un aspecto metodológico de interés es la identificación de los criterios causales. La técnica DEMATEL identifica el coste de construcción, la funcionalidad y las interacciones con la cadena de valor como criterios que inciden en el resto del sistema, mientras que los indicadores ambientales, como la salud humana y la conservación de los ecosistemas, se presentan principalmente como efectos. Esto sugiere que las intervenciones en los costes de construcción y en la organización funcional pueden provocar mejoras indirectas en la sostenibilidad ambiental y social, lo cual resulta relevante al diseñar políticas y contratos que incentiven las prácticas integradas.
Futuras líneas de investigación
Una línea de trabajo inmediata consiste en ampliar la diversidad y el tamaño del panel de agentes consultados para captar las variaciones en las prioridades y las competencias profesionales. Esto permitiría evaluar la sensibilidad de las ponderaciones y mejorar la representatividad social del proceso. Otra opción es trasladar y recalibrar el marco a otros contextos geográficos y tipologías constructivas, como viviendas de mayor altura o equipamientos públicos, para evaluar la transferibilidad de la clasificación y de la estructura causal identificada en este estudio.
En el ámbito técnico, utilizar datos primarios de obras reales en lugar de bases de datos secundarias aumentará la fiabilidad de la evaluación del ciclo de vida (LCA) y del análisis del ciclo de vida (S-LCA) y mejorará la precisión de los modelos de coste del ciclo de vida (LCC). La incorporación de enfoques dinámicos, como la LCA dinámica o las simulaciones acopladas a plataformas BIM, puede facilitar las evaluaciones en etapas iniciales y permitir análisis de sensibilidad más detallados relacionados con la sustitución de componentes, las reparaciones y las evoluciones tecnológicas. Asimismo, explorar técnicas de optimización multiobjetivo que vinculen explícitamente las restricciones económicas con las metas ambientales y sociales podría proporcionar soluciones de diseño más operativas para promotores y organismos públicos.
Desde la perspectiva social, investigar intervenciones concretas de capacitación, reorganización de procesos y de contratos que reduzcan la exposición de los trabajadores a los sistemas industrializados aportará pruebas sobre cómo mantener los beneficios ambientales y económicos sin incrementar los impactos sociales. Por último, el estudio de la interacción entre políticas públicas, incentivos financieros y la adopción tecnológica ofrecerá información útil para diseñar instrumentos que favorezcan soluciones constructivas más equilibradas en el marco de los programas de vivienda social.
Conclusión
El estudio proporciona un marco metodológico replicable y sólido que combina la evaluación del ciclo de vida con técnicas multicriterio capaces de representar las interdependencias y la incertidumbre. Los resultados empíricos indican que, en el caso analizado, las soluciones ligeras industrializadas presentan ventajas en términos de coste y de huella ambiental, aunque se requieren medidas específicas para reducir los riesgos sociales derivados de su ejecución. La metodología y los resultados obtenidos sientan las bases para orientar las políticas y las decisiones de los proyectos y ponen de manifiesto la necesidad de ampliar los datos primarios, diversificar la muestra de expertos y conectar el análisis con herramientas digitales de diseño y gestión.
Os presento un Manual de Referencia sobre la fabricación y la puesta en obra del hormigón. Este libro ofrece una visión integral de la fabricación y la puesta en obra del hormigón, tanto en el ámbito de la edificación como en el de la ingeniería civil. Aborda los equipos y procesos asociados a la preparación del hormigón —incluidas las centrales de hormigonado—, su transporte, vertido, compactación y curado, así como los hormigones especiales, los pavimentos de hormigón para carreteras y el hormigón pretensado. La principal aportación de la obra es su enfoque constructivo, apoyado en abundante material gráfico —fotografías e ilustraciones— que refuerza y clarifica las explicaciones. El texto se completa con una amplia bibliografía, cuestiones de autoevaluación con sus respuestas y problemas resueltos que facilitan la consolidación de los conceptos fundamentales. Concebido como libro de texto para estudiantes de ingeniería y arquitectura, ofrece una orientación práctica clara para la construcción. Al mismo tiempo, está estructurado como un manual de consulta para profesionales vinculados al proyecto y a la ejecución de obras, complementando los contenidos de otros textos de carácter estructural o geotécnico, habitualmente más centrados en el desarrollo teórico y en el cálculo.
