Estoy en proceso de revisión de las pruebas de imprenta del nuevo Manual de Referencia denominado: “Estructuras auxiliares de construcción: andamios, apeos, entibaciones, encofrados y cimbras”. Estará disponible en las librerías durante el mes de septiembre del 2024.
Estoy en proceso de revisión de las pruebas de imprenta del nuevo Manual de Referencia denominado: “Estructuras auxiliares de construcción: andamios, apeos, entibaciones, encofrados y cimbras”. Estará disponible en las librerías durante el mes de septiembre del 2024.
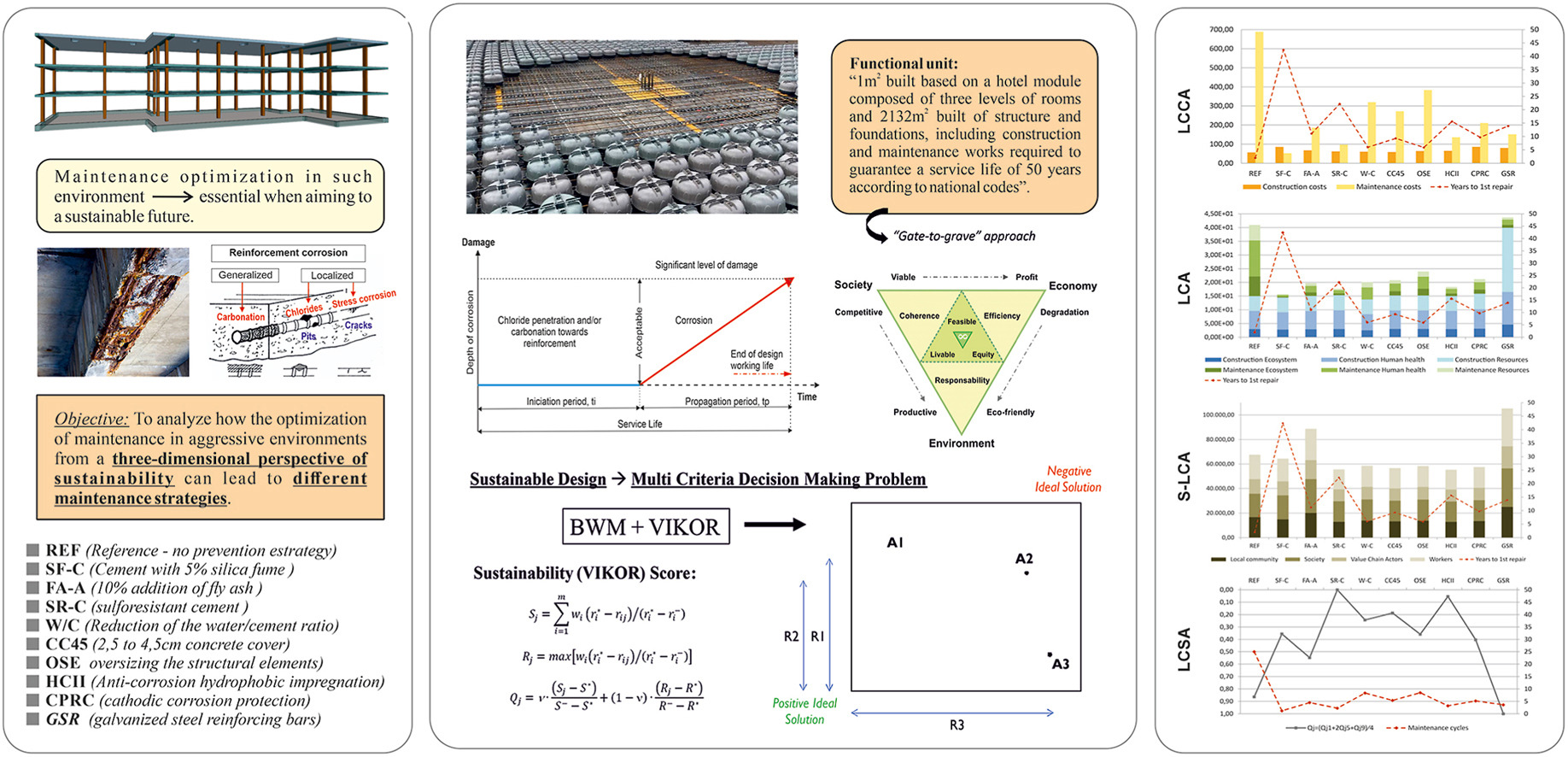
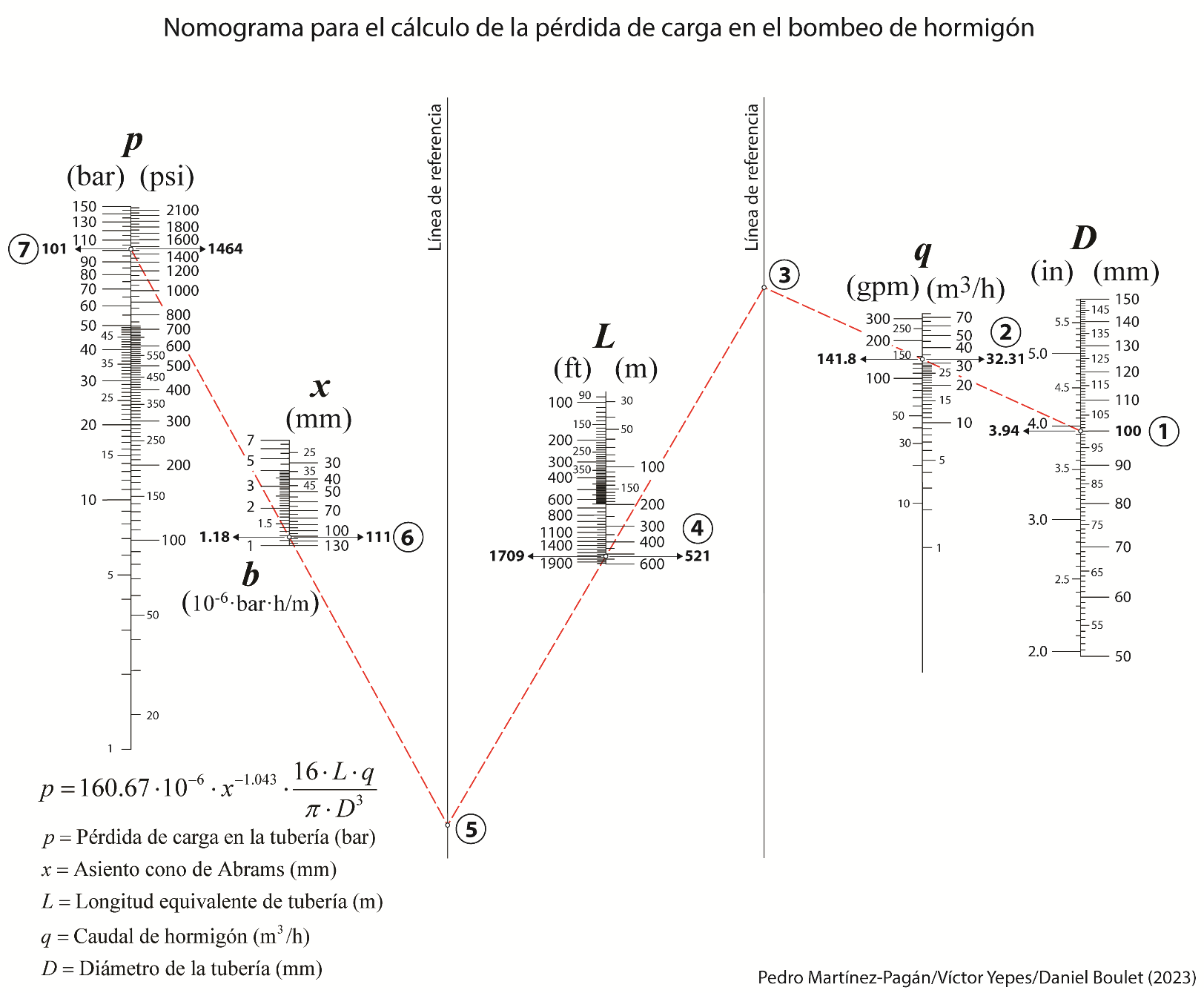
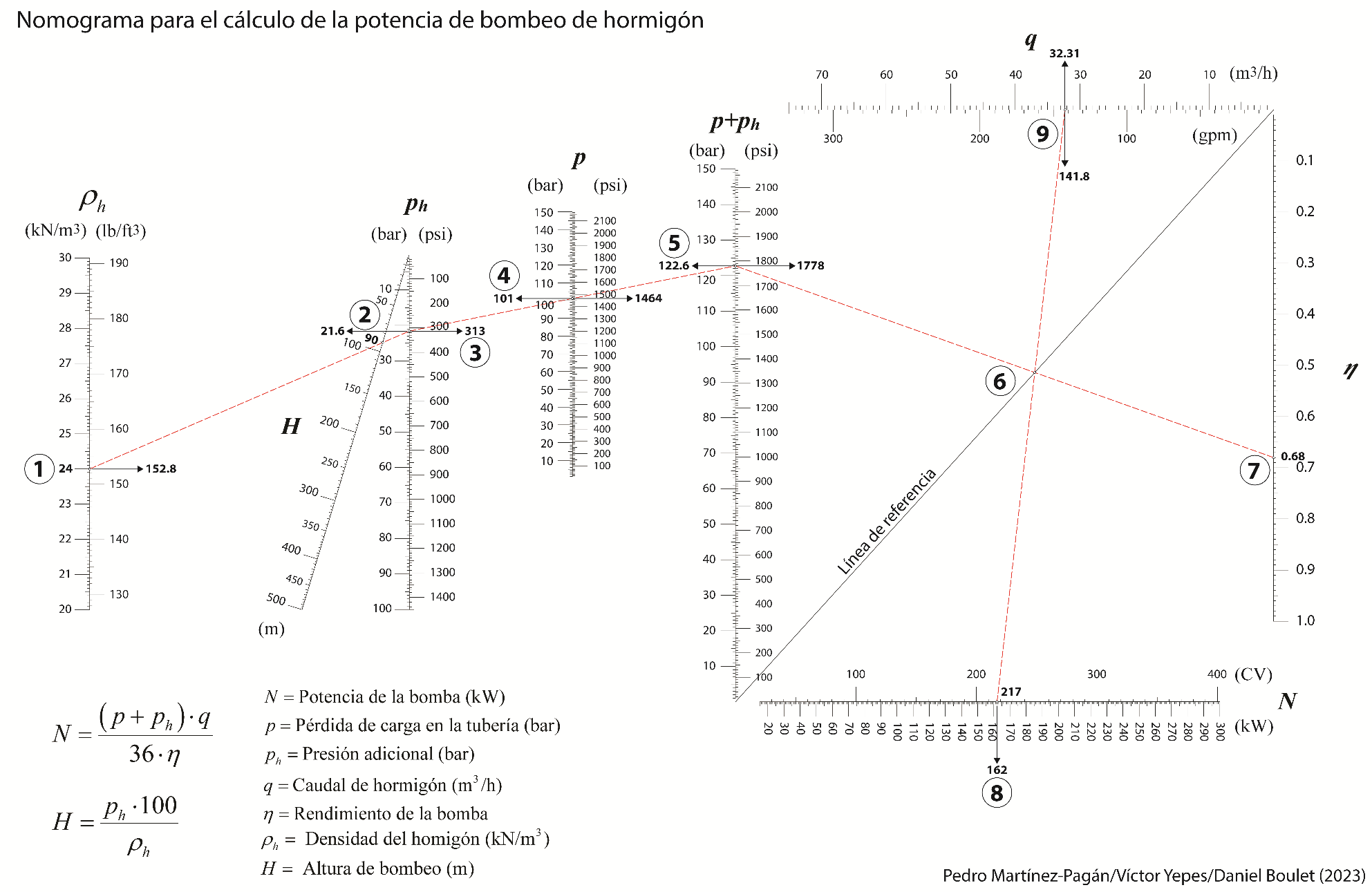
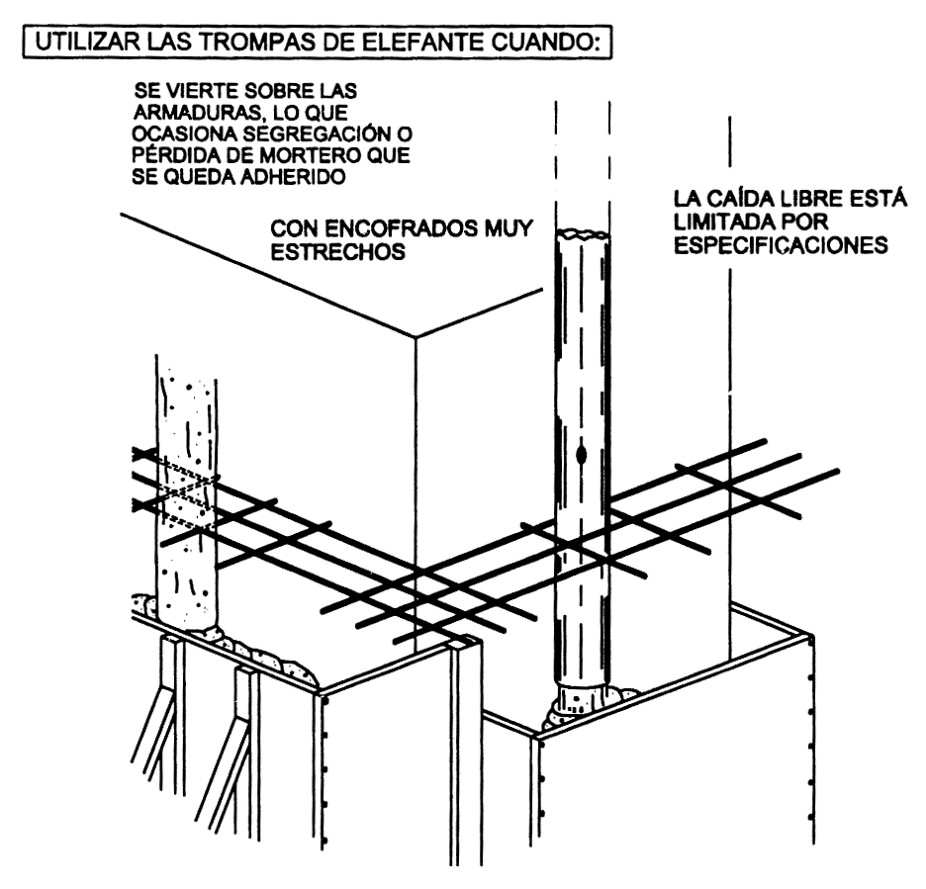
Este libro aborda de manera amplia las estructuras auxiliares utilizadas en la construcción, abarcando tanto el ámbito de la edificación como el de las obras de ingeniería civil. El libro trata de los aspectos relacionados con los apeos y apuntalamientos, las entibaciones, los andamios, los encofrados y las cimbras. La novedad de esta obra radica en el tratamiento constructivo de estas técnicas, donde las fotografías e ilustraciones añaden valor a las explicaciones realizadas en el texto. Además de incluir una amplia bibliografía, se aportan cuestiones de autoevaluación con respuestas para el aprendizaje de los conceptos más importantes, así como problemas resueltos. Es un libro de texto dirigido a estudiantes de ingeniería y arquitectura, con una fuerte orientación hacia la construcción. No obstante, también se estructura como un manual de consulta para los profesionales relacionados con el proyecto y la construcción de obras. Además, este libro complementa los aspectos constructivos de otro tipo de textos estructurales o geotécnicos, más orientados a la teoría y los problemas.
¿Qué es un Manual de Referencia en la Universitat Politècnica de València?
Colección de carácter multidisciplinar, orientada a la formación y al ejercicio profesional. Los contenidos han sido seleccionados por el comité editorial atendiendo a la oportunidad de la obra por su originalidad en el estudio y aplicación de una materia, el apoyo gráfico y práctico con ejercicios demostrativos que sustentan la teoría, la adecuación de su metodología y la revisión bibliográfica actualizada. Los títulos de la colección se clasifican en distintas series según el área de conocimiento y la mayoría de ellos están disponibles tanto en formato papel como electrónico.
Todos los títulos de la colección están evaluados por especialistas en la materia según el método doble ciego, tal como se recoge en la página web de la Editorial (http://www.upv.es/entidades/AEUPV/info/891747normalc.html), garantizando la transparencia en todo el proceso.
Para conocer más información sobre la colección, los títulos que la componen y cómo adquirirlos puede visitar la web, enlace a la página de la colección en www.lalibreria.upv.es
Referencia:
YEPES, V. (2024). Estructuras auxiliares en la construcción: Andamios, apeos, entibaciones, encofrados y cimbras. Colección Manual de Referencia, serie Ingeniería Civil. Editorial Universitat Politècnica de València. Ref. 477
Cursos:
SOBRE EL AUTOR:
Víctor Yepes Piqueras. Catedrático de universidad del Departamento de Ingeniería de la Construcción y Proyectos de Ingeniería Civil de la Universitat Politècnica de València. Número 1 de su promoción, ha desarrollado su vida profesional en empresas constructoras, en el sector público y en el ámbito universitario. Ha recibido el Premio a la Excelencia Docente por parte del Consejo Social de la UPV. Es investigador del Instituto de Ciencia y Tecnología del Hormigón (ICITECH) y profesor visitante en la Pontificia Universidad Católica de Chile. Ha sido director académico del Máster Universitario en Ingeniería del Hormigón (acreditado con el sello EUR-ACE). Imparte docencia en asignaturas de grado y posgrado relacionadas con procedimientos de construcción y gestión de obras, calidad e innovación, modelos predictivos y optimización en la ingeniería. Sus líneas de investigación actuales se centran en la optimización multiobjetivo, la sostenibilidad y el análisis de ciclo de vida de puentes y estructuras de hormigón.