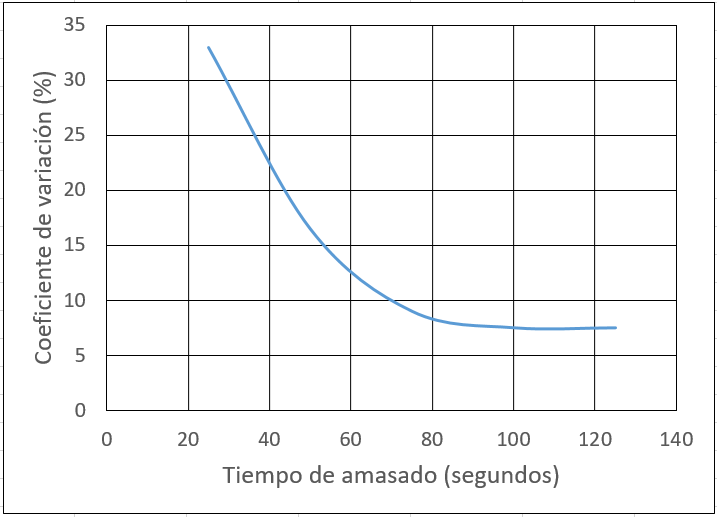
En general, no se requieren equipos especiales para fabricar hormigón autocompactante; se pueden utilizar las amasadoras convencionales empleadas para el hormigón compactable por vibración. Sin embargo, es fundamental controlar continuamente el contenido de humedad de los áridos y ajustar el agua de amasado en función de los resultados de este control. Además, es necesario establecer un esquema de control casi continuo durante la elaboración de las primeras mezclas, ajustando los tiempos de amasado en función de los resultados. Cabe señalar que, por lo general, los tiempos de amasado para el hormigón autocompactante deben ser ligeramente mayores que para los hormigones convencionales.
Dado que el hormigón autocompactante no requiere compactación para su colocación y es capaz de fluir dentro del encofrado, llenando naturalmente su volumen y consolidándose bajo su propio peso, los rendimientos de colocación son mucho mayores que los del hormigón convencional. En elementos horizontales, como losas de piso, forjados, soleras o pavimentos, estos rendimientos son aún mayores, lo que permite reducir los tiempos de ejecución hasta en un 20 o 25 %, dependiendo de la naturaleza de la construcción. Esta reducción en los tiempos de ejecución va acompañada de una disminución del 50 % en la mano de obra necesaria para su colocación, lo cual compensa su mayor coste respecto a otros hormigones.
Otro factor a considerar es que se necesita menos equipo para colocar el hormigón autocompactante. Ya sea vertido directamente desde el camión mezclador o a través de un tubo flexible de goma cuando se utiliza un sistema de bombeo, no es necesario emplear equipos como palas y rastrillos para colocarlo ni llanas para acabarlo. Además, al eliminar la actividad de vibrado del material, se prescinde del uso de equipos de compactación necesarios para el hormigón convencional.

El momento en el que deben añadirse los aditivos, especialmente los superplastificantes, debe determinarse en consulta con el proveedor. Asimismo, una vez seleccionada la dosificación, cualquier problema con la consistencia de la masa debe resolverse preferiblemente ajustando la dosificación de los aditivos, particularmente la cantidad de superplastificante, siempre y cuando la relación agua/cemento permita realizar estas correcciones sin superar los límites establecidos en los ensayos de dosificación.
La fabricación del hormigón autocompactante es similar a la del hormigón convencional vibrado, pero requiere una mayor atención a la regularidad de la dosificación. Esto se debe a que el hormigón autocompactante es más exigente en términos de uniformidad de los materiales y precisión en la dosificación del agua. Debido a su mayor cohesión, es preferible amasar el hormigón autocompactante con dos tercios de la cantidad total de agua. Una vez que se haya logrado una buena homogeneización, se debe añadir el tercio restante de agua junto con los aditivos necesarios para completar el amasado.
Al suministrar el hormigón en la obra, puede ser conveniente volver a readitivar el material para asegurar que mantiene las condiciones de autocompactabilidad necesarias para su correcta colocación. La readitivación debe realizarse bajo la supervisión del fabricante del hormigón, quien determinará el tipo y la dosis exacta de aditivo necesarios, así como verificará que el tiempo de amasado en el camión después de la readitivación sea el adecuado.
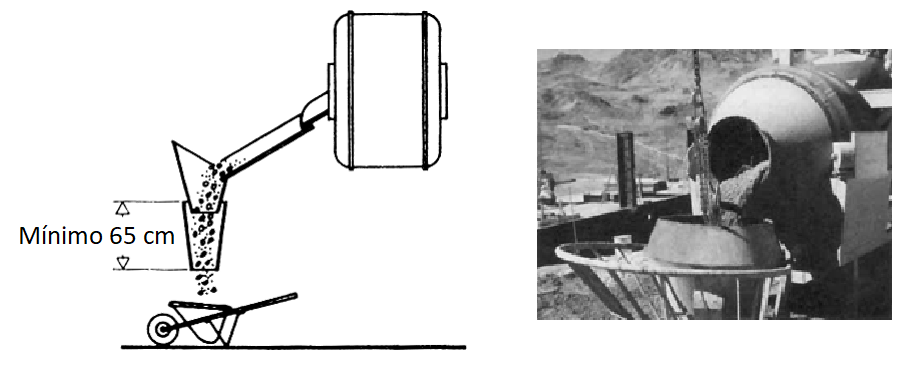
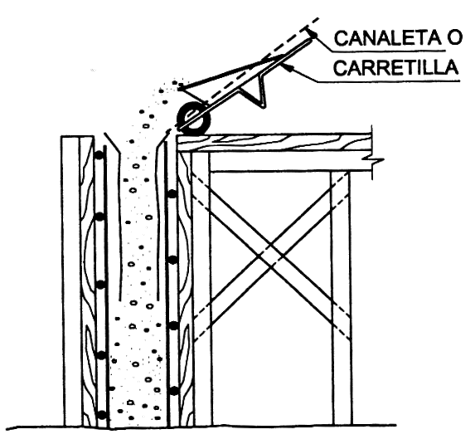
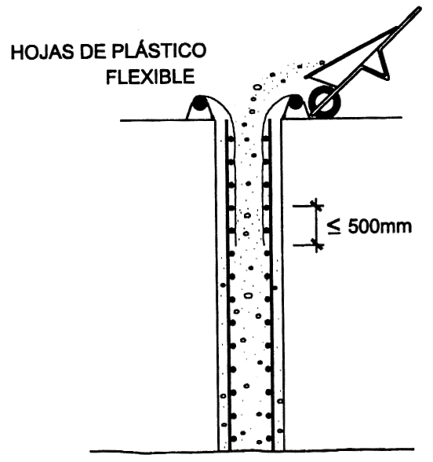
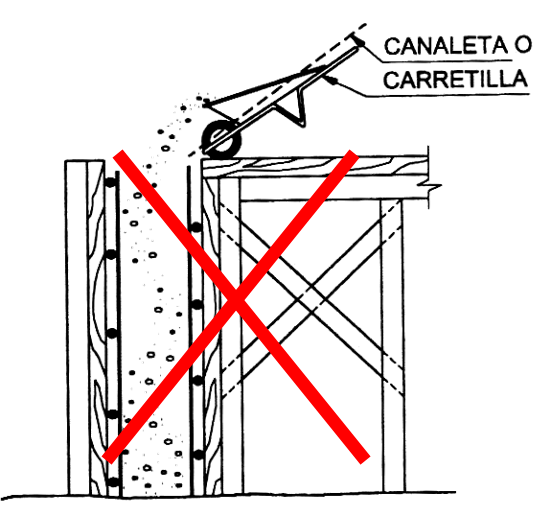
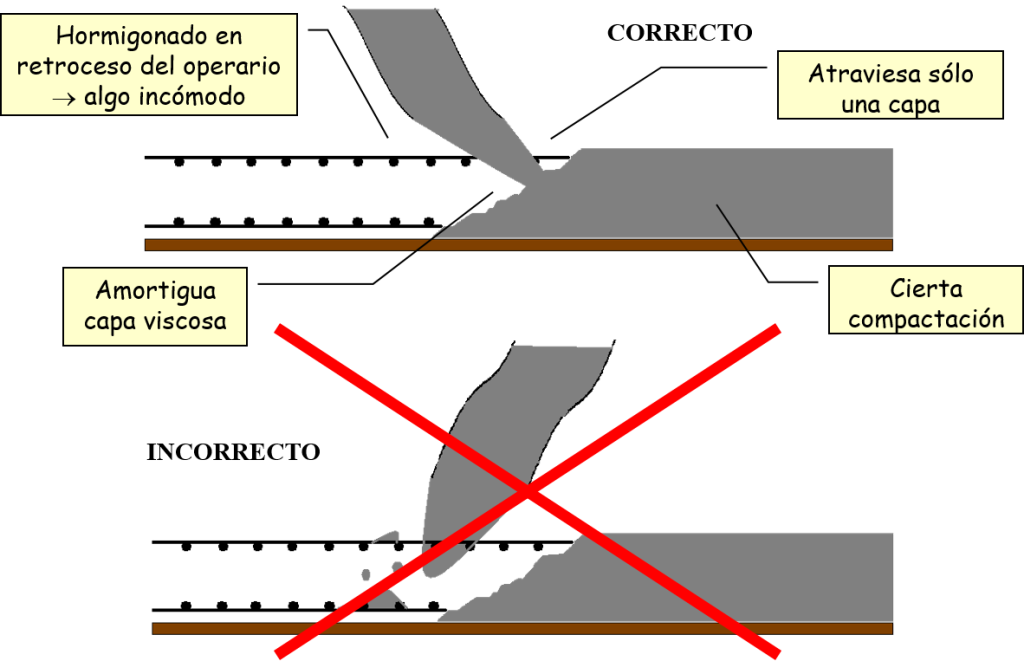
Se recomienda el uso de la técnica de hormigonado con bomba para este tipo de hormigón. Para obtener mejores resultados, el hormigón debe bombearse desde la parte más baja del encofrado. Si se opta por el hormigonado por caída libre, la altura de vertido no debe superar los 5 m y la distancia horizontal de desplazamiento debe limitarse a un máximo de 10 m para evitar la segregación del material.
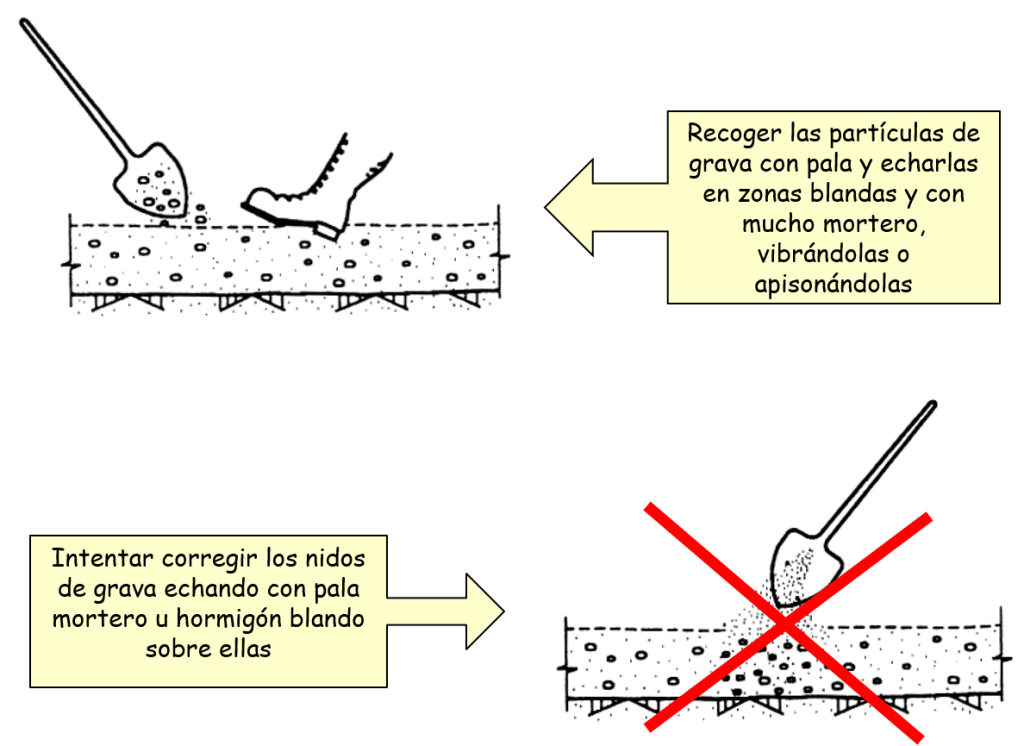
Los encofrados deben ser no absorbentes, y es fundamental prestar especial atención a su diseño, ya que el hormigón autocompactante ejerce presiones mayores durante su colocación. Dado que el hormigón autocompactante es un material muy fluido, los encofrados deben ser estancos. Esto evita que la lechada se filtre por las juntas y provoque la formación de «nidos de grava» una vez desencofrado el elemento.
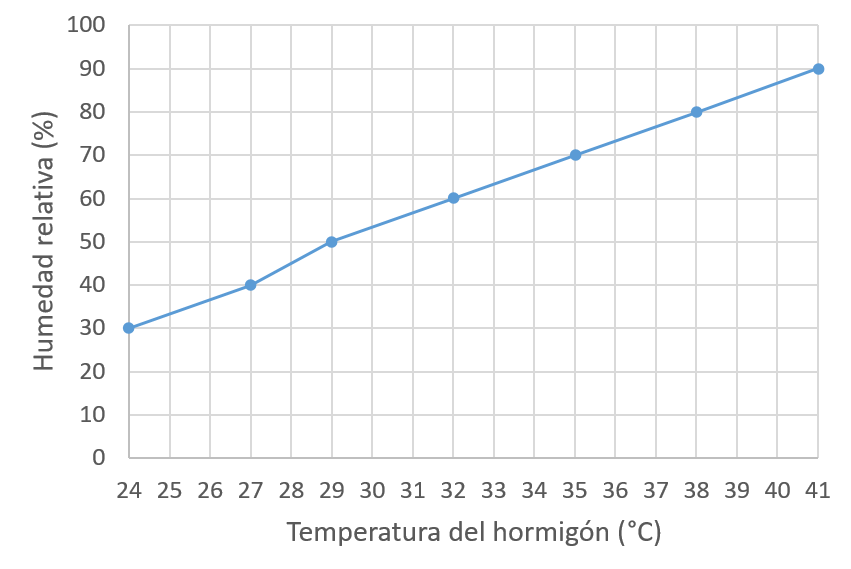
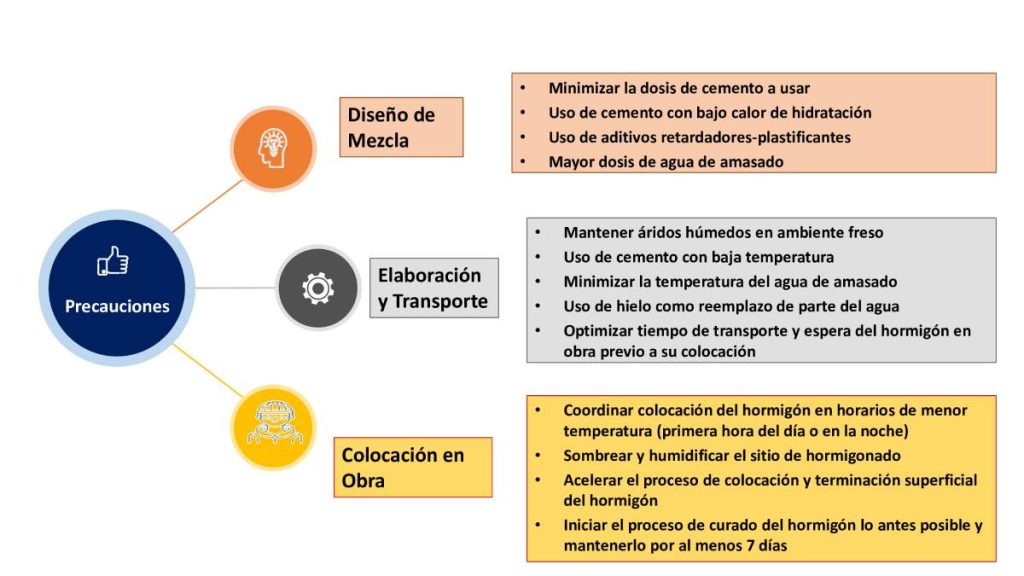
El curado del hormigón autocompactante es similar al del hormigón convencional y se aplican los mismos procedimientos. Es importante comenzar el curado lo antes posible para evitar la pérdida de agua superficial por evaporación, lo que podría causar retracción plástica y asentamiento, especialmente en condiciones adversas como altas temperaturas, viento y baja humedad relativa. Estos factores son aún más críticos cuando se combinan. Además, dado que el hormigón autocompactante contiene más finos (cemento y aditivos) que el hormigón convencional, el curado adquiere mayor importancia.
Se pueden emplear los mismos procedimientos para el acabado de las superficies de hormigón autocompactante en términos de textura y color que los utilizados para el hormigón convencional.
En superficies sin tratamiento adicional, el hormigón autocompactante ofrece una mayor uniformidad y, por lo tanto, un mejor acabado en comparación con el hormigón convencional. Esto se debe a que, al evitar la vibración, se elimina el principal factor que provoca la falta de homogeneidad cromática en las caras visibles del hormigón. En el hormigón convencional, esta heterogeneidad se debe a la distribución aleatoria del agua en la mezcla, lo que genera diferentes procesos de hidratación con variadas proporciones de agua y cemento, que dan lugar a variaciones en el color del cemento hidratado. No obstante, hay que tener precaución con los niveles de acabado en las superficies libres, procediendo a su nivelación y acabado superficial con útiles especiales, dado que la aplicación de reglas metálicas resulta problemática en algunas ocasiones.
Os dejo, a continuación, algunos vídeos ilustrativos.
Referencias:
ACI COMMITTEE 304. Guide for Measuring, Mixing, Transporting, and Placing Concrete. ACI 304R-00.
BUSTILLO, M. (2008). Hormigones y morteros. Fueyo Editores, Madrid, 721 pp.
CALAVERA, J. et al. (2004). Ejecución y control de estructuras de hormigón. Intemac, Madrid, 937 pp.
FERNÁNDEZ CÁNOVAS, M. (2004). Hormigón. 7ª edición, Colegio de Ingenieros de Caminos, Canales y Puertos. Servicio de Publicaciones, Madrid, 663 pp.
GALABRU, P. (1964). Tratado de procedimientos generales de construcción. Obras de fábrica y metálicas. Editorial Reverté, Barcelona, 610 pp.
MARTÍ, J.V.; YEPES, V.; GONZÁLEZ, F. (2014). Fabricación, transporte y colocación del hormigón. Apuntes de la Universitat Politècnica de València, 189 pp.
TIKTIN, J. (1994). Procesamiento de áridos: instalaciones y puesta en obra de hormigón. Universidad Politécnica de Madrid. Escuela Técnica Superior de Ingenieros de Caminos, Canales y Puertos. Madrid, 360 pp. ISBN: 84-7493-205-X.
YEPES, V. (2020). Procedimientos de construcción de cimentaciones y estructuras de contención. Colección Manual de Referencia, 2ª edición. Editorial Universitat Politècnica de València, 480 pp. Ref. 328. ISBN: 978-84-9048-903-1.
YEPES, V. (2023). Maquinaria y procedimientos de construcción. Problemas resueltos. Colección Académica. Editorial Universitat Politècnica de València, 562 pp. Ref. 376. ISBN 978-84-1396-174-3

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.