 Introducción: Atrapado en lo «suficientemente bueno».
Introducción: Atrapado en lo «suficientemente bueno».
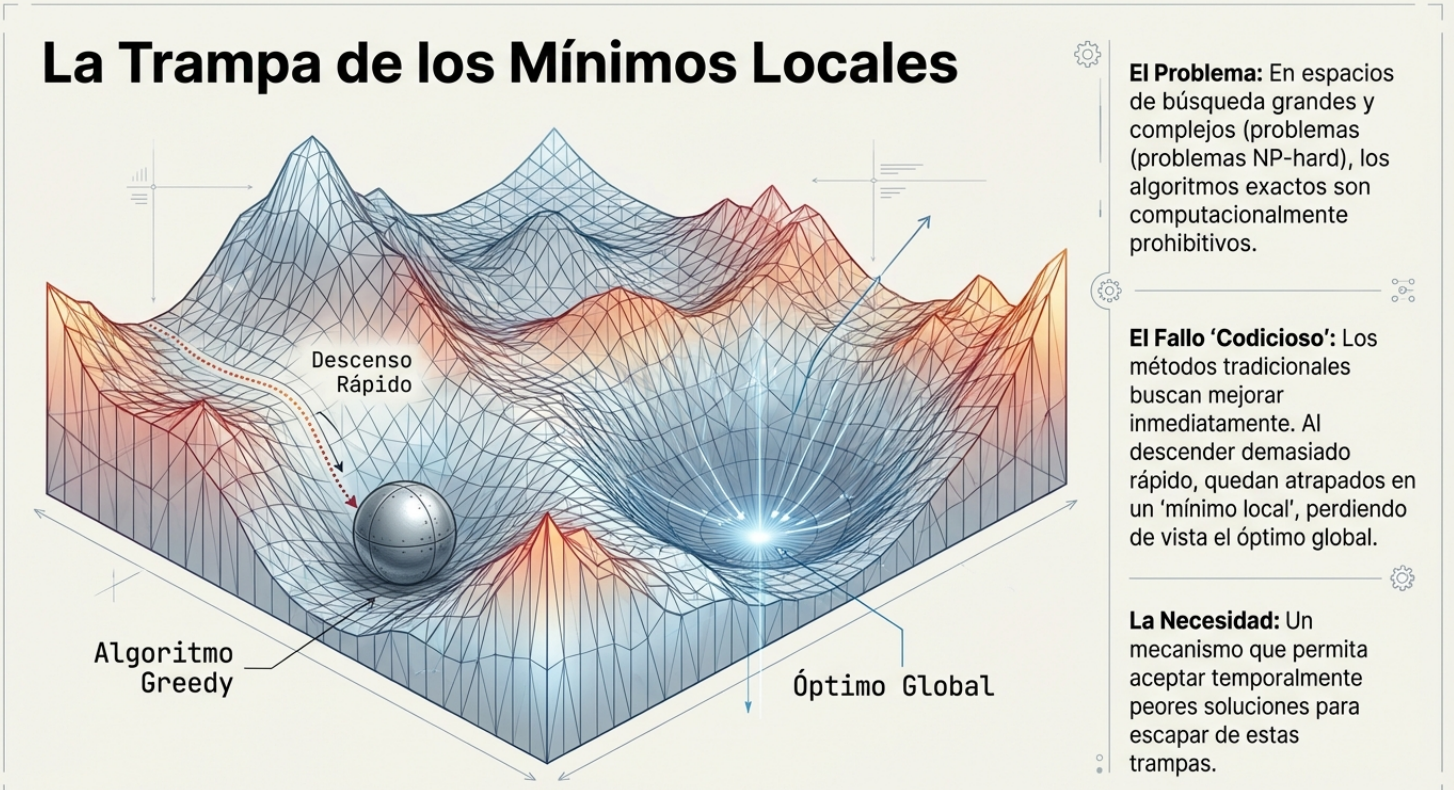
¿Alguna vez has sentido que encontraste una solución funcional a un problema, pero tenías la persistente sensación de que existía una respuesta mucho mejor? En la vida y en la tecnología, es fácil quedarse atascado en una solución «buena», pero no óptima, en un callejón sin salida conocido como «mínimo local». Salir de ahí requiere una estrategia poco convencional.
Es aquí donde entra en juego el recocido simulado, una ingeniosa metaheurística estocástica que toma su inspiración de la metalurgia. Desarrollado de forma independiente por Kirkpatrick, Gelatt y Vecchi en 1983 y por Černý en 1985, este algoritmo es, en esencia, una estrategia de búsqueda inteligente que utiliza la aleatoriedad de forma controlada para encontrar soluciones óptimas en problemas de gran complejidad.
Este artículo explora las lecciones más sorprendentes y contraintuitivas que este poderoso algoritmo puede enseñarnos para abordar y resolver problemas verdaderamente complejos.
1. El secreto está en la metalurgia: un algoritmo que piensa como un herrero.
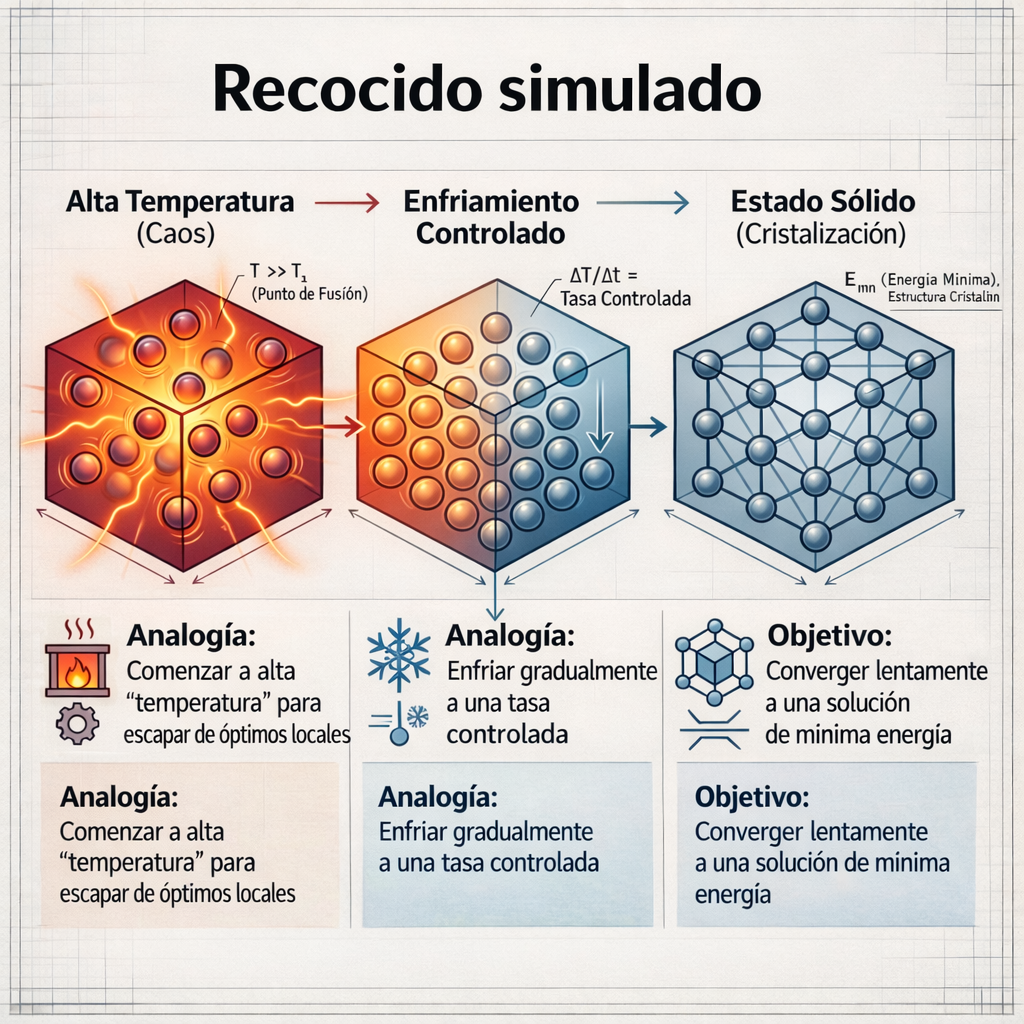
La genialidad del recocido simulado radica en su analogía directa con el proceso de recocido de metales. El herrero calienta el metal a altas temperaturas y luego lo enfría lentamente y de forma controlada para eliminar sus imperfecciones y lograr una estructura interna sólida y estable. El algoritmo hace exactamente lo mismo, pero en el mundo abstracto de los datos y las soluciones.
Los conceptos clave de esta analogía son:
- «Temperatura» alta: al principio, el algoritmo opera a una «temperatura» elevada. Esto corresponde a una fase de exploración amplia, en la que se consideran muchísimas soluciones posibles, incluso las que parecen malas, para obtener una visión global del problema.
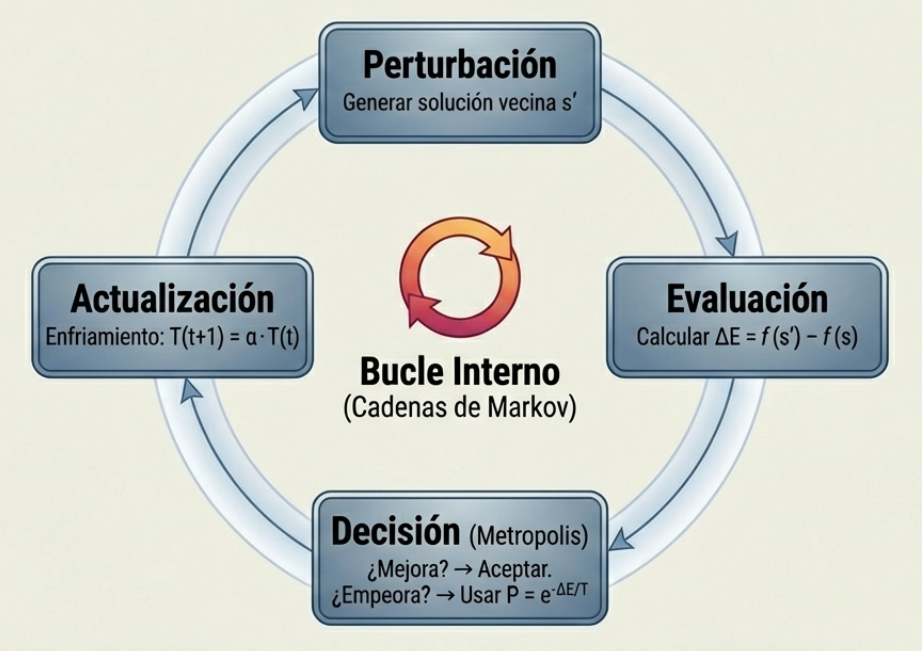
- «Enfriamiento» controlado: a medida que avanza el proceso, la «temperatura» se reduce gradualmente. Este «enfriamiento» suele seguir un programa geométrico (como Tt + 1 = α·Tt), lo que obliga al algoritmo a ser más selectivo. Se pasa de la exploración a la explotación, enfocándose progresivamente en las regiones más prometedoras.
- «Energía» del sistema: en el algoritmo, la «energía» de una configuración corresponde a la función objetivo que se busca optimizar (por ejemplo, minimizar el coste, la distancia o el error).
- «Estructura cristalina estable» de baja energía: el objetivo final del recocido es lograr un estado de mínima energía que, en el ámbito de la optimización, representa la solución óptima o casi óptima del problema.
2. La estrategia contraintuitiva: aceptar un empeoramiento para poder mejorar.
La característica más paradójica y, a la vez, más poderosa del recocido simulado es su capacidad para aceptar movimientos que, en un principio, empeoran la solución actual. Esa es la esencia de la exploración: a diferencia de los algoritmos «codiciosos» que solo aceptan mejoras, este método sabe que, a veces, hay que atravesar un pequeño valle para escalar una montaña más alta.
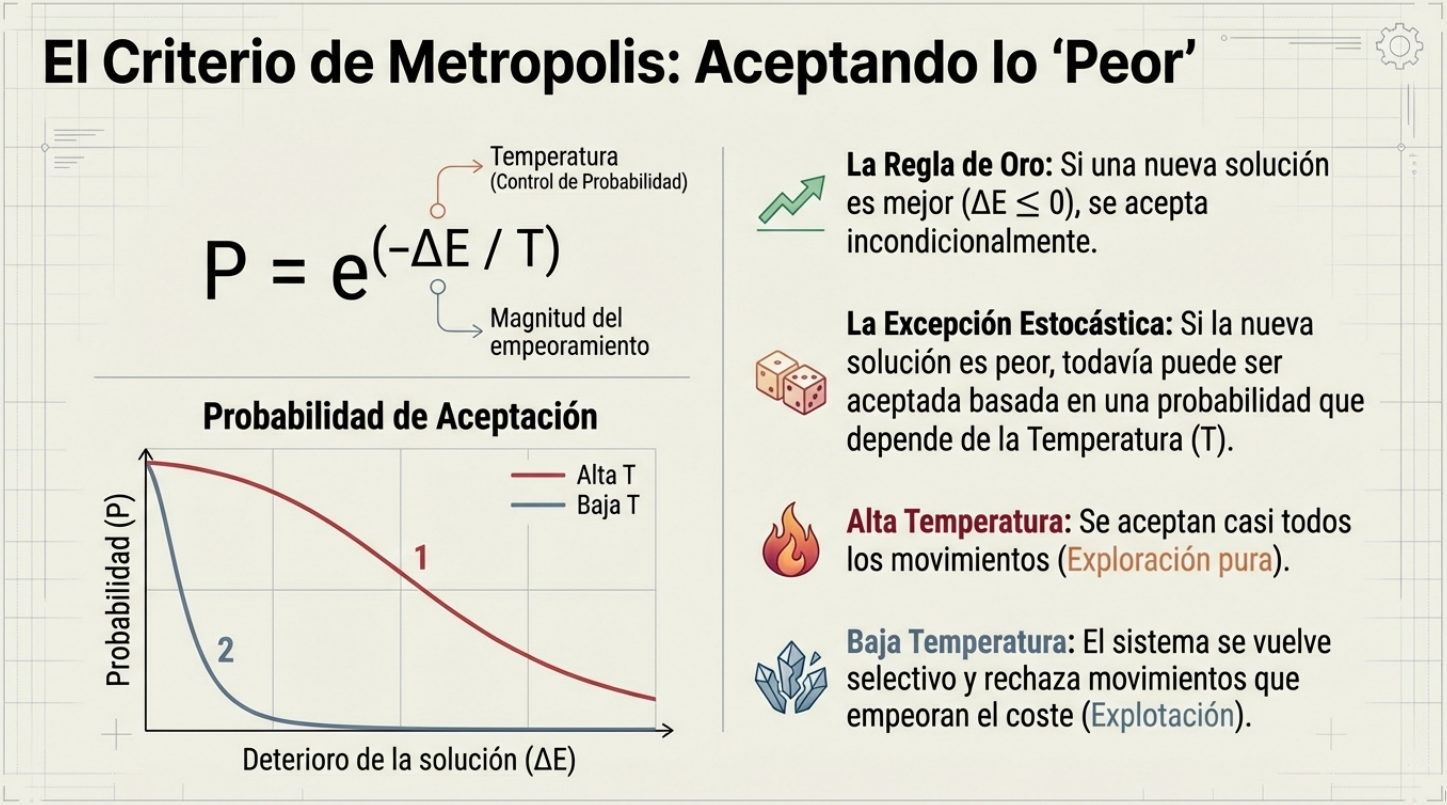
No se trata de un error, sino de una estrategia deliberada para evitar quedar atrapado en los mínimos locales. Antes de reducir la temperatura, el algoritmo ejecuta una serie de iteraciones (una cadena de Markov) para explorar a fondo el entorno de la solución actual. La probabilidad de aceptar un «mal» movimiento es mayor cuando la «temperatura» es alta y disminuye a medida que el sistema se «enfría», según el factor de Boltzmann exp(-ΔE/T). Al principio, la exploración es agresiva, pero al final el algoritmo se vuelve mucho más selectivo.
«Esta aceptación controlada de transiciones no mejoradoras permite al algoritmo escapar de los mínimos locales y evitar una convergencia prematura».
3. La perfección es enemiga de lo práctico: por qué «casi óptimo» es un gran resultado.
Teóricamente, para garantizar que el recocido simulado encuentre la solución globalmente óptima, podría requerir un tiempo de ejecución infinito. Sin embargo, su verdadero valor no radica en la perfección teórica, sino en su gran pragmatismo. La lección fundamental aquí es el equilibrio entre la perfección teórica y la aplicación práctica.
El algoritmo «produce de forma consistente soluciones de alta calidad en escalas de tiempo computacionales prácticas». En ingeniería, logística o finanzas, donde los recursos y el tiempo son limitados, una solución excelente entregada a tiempo es mucho más valiosa que una solución perfecta que nunca se entrega. El recocido simulado encarna este principio de diseño esencial: optimizar para el mundo real, no para un ideal teórico.
4. De vendedores viajeros a puentes de hormigón: la asombrosa versatilidad del algoritmo.
La solidez del recocido simulado se evidencia en la increíble diversidad de problemas que puede resolver. Su capacidad para explorar paisajes de soluciones complejos lo convierte en una herramienta fiable cuando no existen solucionadores específicos para un problema.
Algunos de sus campos de aplicación más impactantes incluyen:
- Rutas y logística: Ha demostrado su eficacia al resolver el problema del vendedor viajero (TSP), encontrando rutas óptimas para conectar múltiples ciudades.
- Procesamiento de imágenes: Se utiliza en la restauración de imágenes dañadas o con ruido, así como para resolver problemas de segmentación complejos.
- Química molecular: Es una herramienta estándar en la cristalografía de macromoléculas que permite determinar la estructura tridimensional de moléculas complejas.
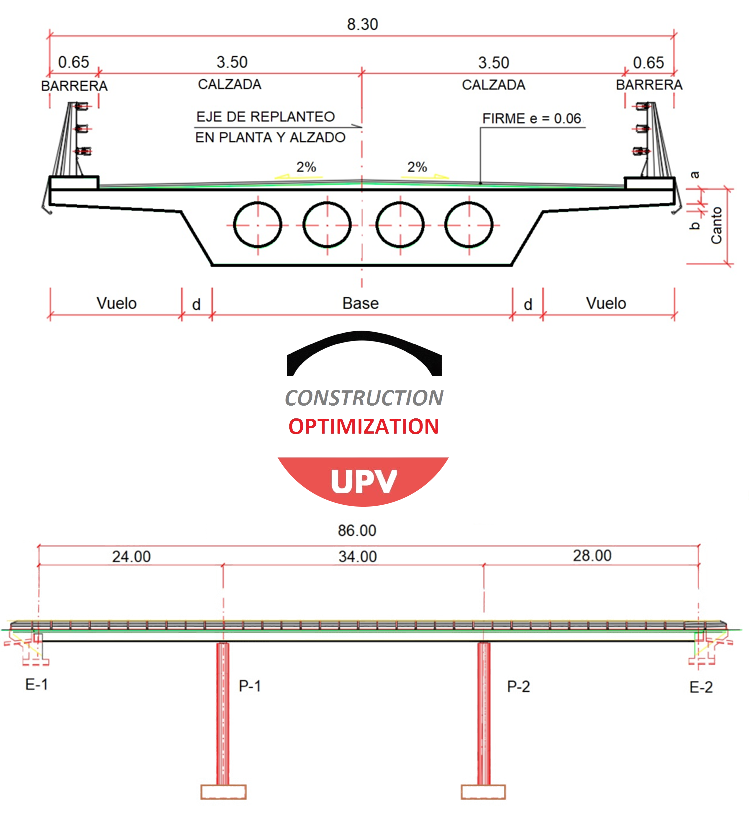
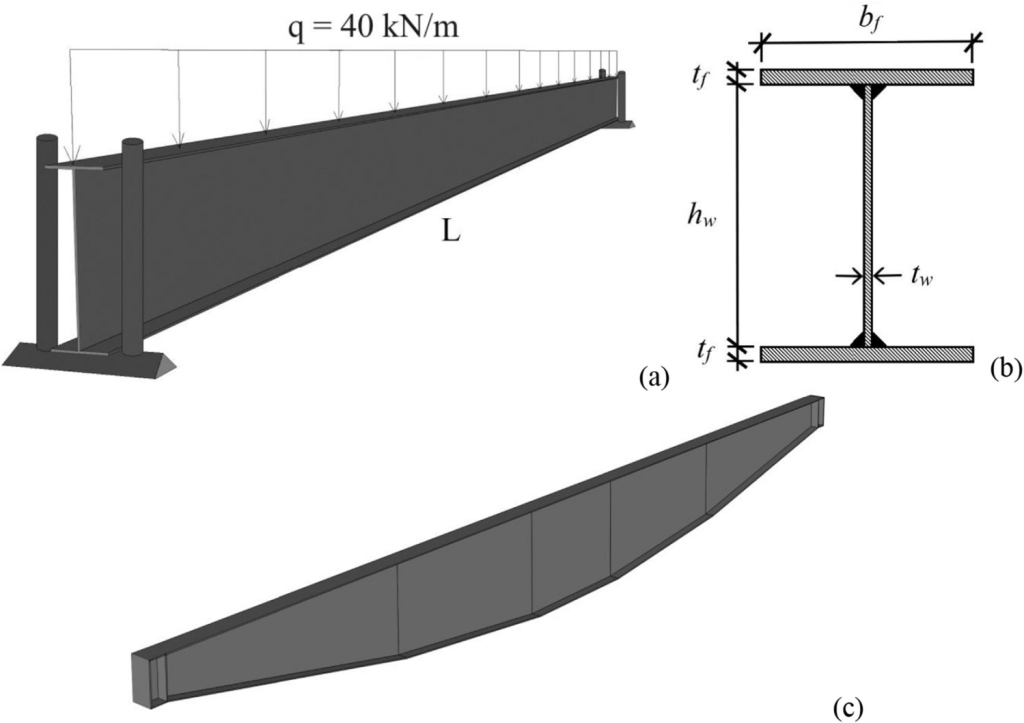
- Ingeniería estructural: Permite realizar optimizaciones de gran impacto, como el diseño de puentes de hormigón pretensado, muros de contención de bajo coste y, en especial, la minimización simultánea del coste y de las emisiones de CO₂ en el diseño de columnas de hormigón armado.
5. A veces, una regla simple supera al azar: la alternativa determinista.
Un giro interesante en la historia de este algoritmo es la variante llamada «Aceptación por umbral» (TA, por sus siglas en inglés). Este método sustituye la regla de aceptación probabilística del recocido simulado por una regla determinista mucho más sencilla.
En lugar de calcular una probabilidad, TA solo acepta una solución peor si el empeoramiento es inferior a un umbral predefinido. Este umbral, al igual que la temperatura del algoritmo original, disminuye gradualmente a lo largo del proceso. Lo sorprendente es el resultado: estudios empíricos han demostrado que, en ciertos problemas como la planificación de tareas, la planificación forestal y la asignación de recursos, este método más simple «puede tener un rendimiento comparable o incluso superior al SA». Una lección de que, a veces, la solución más elegante no es la más compleja.
Conclusión: ¿te atreves a dar un paso atrás?
La gran lección del recocido simulado es una profunda metáfora de la resolución de problemas: el progreso no siempre es una línea recta. La verdadera optimización requiere dominar el cambio gradual, desde una exploración audaz hasta una explotación enfocada. Aceptar retrocesos temporales y controlados no es un signo de fracaso, sino una estrategia inteligente para alcanzar un objetivo mucho más alto a largo plazo.
La próxima vez que te enfrentes a un problema complejo, ¿te atreverás a explorar un camino que parezca peor al principio para encontrar una solución verdaderamente excepcional al final?
En esta conversación puedes escuchar las ideas más interesantes sobre el tema.
Este vídeo resume bien los conceptos más importantes del Simulated Annealing.
Te dejo un documento que puede interesarte.
Recocido_Simulado_Del_Caos_a_la_Solución
Referencia:
Yepes, V. (2026). Heuristic Optimization Using Simulated Annealing. In: Kulkarni, A.J., Mezura-Montes, E., Bonakdari, H. (eds) Encyclopedia of Engineering Optimization and Heuristics. Springer, Singapore. https://doi.org/10.1007/978-981-96-8165-5_48-1

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.