Etiqueta: teoría de juegos

Tesis doctoral: Optimal deep learning assisted design of socially and environmentally efficient steel concrete composite bridges under constrained budgets

Hoy 19 de julio de 2023 ha tenido lugar la defensa de la tesis doctoral de D. David Martínez Muñoz titulada “Optimal deep learning assisted design of socially and environmentally efficient steel concrete composite bridges under constrained budgets“, dirigida por Víctor Yepes Piqueras y José V. Martí Albiñana. La tesis recibió la máxima calificación de sobresaliente “cum laude” y presenta la mención internacional. Presentamos a continuación un pequeño resumen de la misma.

Resumen:

El diseño de infraestructuras está fuertemente influido por la búsqueda de soluciones que tengan en cuenta el impacto en la economía, el medio ambiente y la sociedad. Estos criterios están muy relacionados con la definición de sostenibilidad que hizo la Comisión Brundtland en 1987. Este hito supuso un reto para técnicos, científicos y legisladores. Este reto consistía en generar métodos, criterios, herramientas y normativas que permitieran incluir el concepto de sostenibilidad en el desarrollo y diseño de nuevas infraestructuras. Desde entonces, se han producido pequeños avances en la búsqueda de la sostenibilidad, pero se necesitan más a corto plazo. Como plan de acción, las Naciones Unidas establecieron los Objetivos de Desarrollo Sostenible, fijando el año 2030 como meta para alcanzarlos. Dentro de estos objetivos, las infraestructuras se postulan como un punto crítico. Tradicionalmente, se han desarrollado métodos para obtener diseños óptimos desde el punto de vista del impacto económico. Sin embargo, aunque en los últimos tiempos se ha avanzado en la aplicación y utilización de métodos de análisis del ciclo de vida completo, aún falta un consenso claro, especialmente en el pilar social de la sostenibilidad. Dado que la sostenibilidad engloba diferentes criterios, que en principio no van necesariamente de la mano, el problema de la búsqueda de la sostenibilidad se plantea no solo como un problema de optimización, sino también como un problema de toma de decisiones multi-criterio.

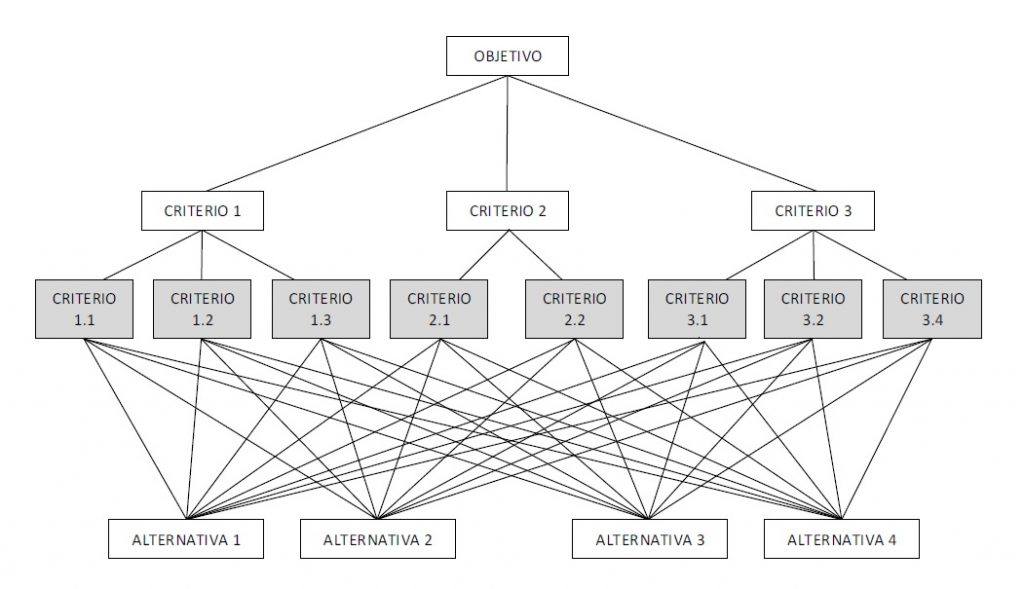
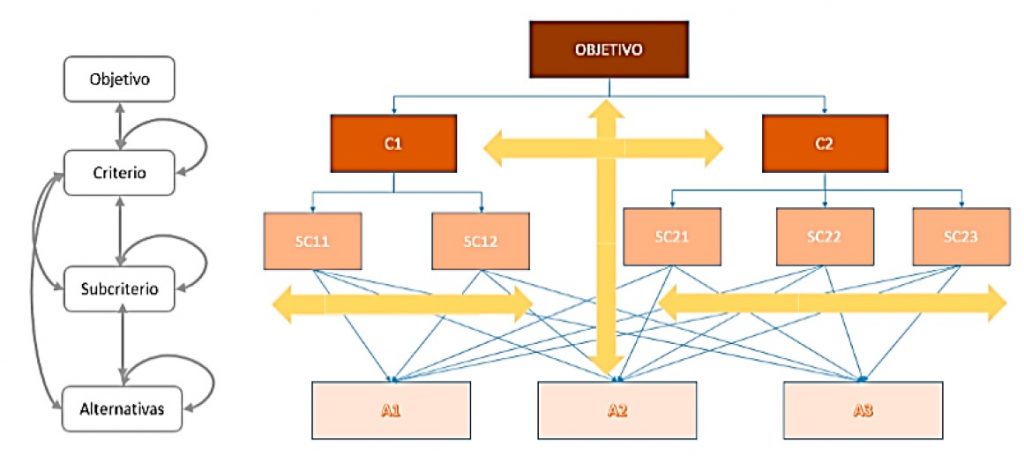
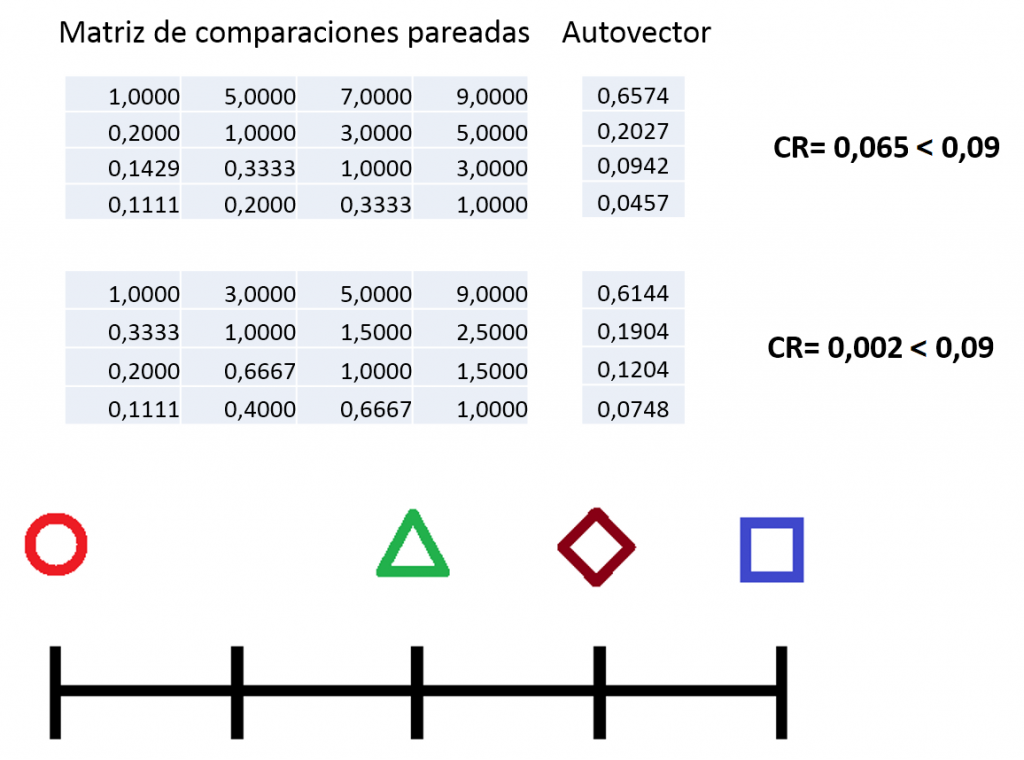
El objetivo principal de esta tesis doctoral es proponer diferentes metodologías para la obtención de diseños óptimos que introduzcan los pilares de la sostenibilidad en el diseño de puentes mixtos acero-hormigón. Como problema estructural representativo se sugiere un puente viga en cajón de tres vanos mixto. Dada la complejidad de la estructura, en la que intervienen 34 variables discretas, la optimización con métodos matemáticos resulta inabordable. Por ello, se recomienda el uso de algoritmos metaheurísticos. Esta complejidad también se traduce en un alto coste computacional para el modelo, por lo que se implementa un modelo de redes neuronales profundas que permite la validación del diseño sin necesidad de computación. Dada la naturaleza discreta del problema, se proponen técnicas de discretización para adaptar los algoritmos al problema de optimización estructural. Además, para mejorar las soluciones obtenidas a partir de estos algoritmos discretos, se introducen métodos de hibridación basados en la técnica K-means y operadores de mutación en función del tipo de algoritmo. Los algoritmos utilizados se clasifican en dos ramas. La primera son los basados en trayectorias como el Simulated Annealing, Threshold Accepting y el Algoritmo del Solterón. Por otra parte, se emplean algoritmos de inteligencia de enjambre como Jaya, Sine Cosine Algorithm y Cuckoo Search. La metodología de Análisis del Ciclo de Vida definida en la norma ISO 14040 se usa para evaluar el impacto social y medioambiental de los diseños propuestos. La aplicación de esta metodología permite evaluar el impacto y compararlo con otros diseños. La evaluación mono-objetivo de los diferentes criterios lleva a la conclusión de que la optimización de costes está asociada a una reducción del impacto medioambiental y social de la estructura. Sin embargo, la optimización de los criterios medioambientales y sociales no reduce necesariamente los costes. Por ello, para realizar una optimización multi-objetivo y encontrar una solución de compromiso, se implementa una técnica basada en la Teoría de Juegos, recomendando una estrategia de juego cooperativo. La técnica multi-criterio empleada es la Teoría de la Entropía para asignar pesos a los criterios para la función objetivo agregada. Los criterios considerados son los tres pilares de la sostenibilidad y la facilidad constructiva de la losa superior. Aplicando esta técnica se obtiene un diseño óptimo relativo a los tres pilares de la sostenibilidad y a partir del cual se mejora la facilidad constructiva.

Referencias:

MARTÍNEZ-MUÑOZ, D.; GARCÍA, J.; MARTÍ, J.V.; YEPES, V. (2023). Hybrid swarm intelligence optimization methods for low-embodied energy steel-concrete composite bridges. Mathematics, 11(1):140. DOI:10.3390/math11010140

MARTÍNEZ-MUÑOZ, D.; GARCÍA, J.; MARTÍ, J.V.; YEPES, V. (2022). Optimal design of steel-concrete composite bridge based on a transfer function discrete swarm intelligence algorithm. Structural and Multidisciplinary Optimization, 65:312. DOI:10.1007/s00158-022-03393-9

GARCÍA, J.; VILLAVICENCIO, G.; ALTIMIRAS, F.; CRAWFORD, B.; SOTO, R.; MINTATOGAWA, V.; FRANCO, M.; MARTÍNEZ-MUÑOZ, D.; YEPES, V. (2022). Machine learning techniques applied to construction: A hybrid bibliometric analysis of advances and future directions. Automation in Construction, 142:104532. DOI:10.1016/j.autcon.2022.104532

MARTÍNEZ-MUÑOZ, D.; GARCÍA, J.; MARTÍ, J.V.; YEPES, V. (2022). Discrete swarm intelligence optimization algorithms applied to steel-concrete composite bridges. Engineering Structures, 266:114607. DOI:10.1016/j.engstruct.2022.114607

MARTÍNEZ-MUÑOZ, D.; MARTÍ, J.V.; YEPES, V. (2022). Social Impact Assessment Comparison of Composite and Concrete Bridge Alternatives. Sustainability, 14(9):5186. DOI:10.3390/su14095186.

ATA-ALI, N.; PENADÉS-PLÀ, V.; MARTÍNEZ-MUÑOZ, D.; YEPES, V. (2021). Recycled versus non-recycled insulation alternatives LCA analysis for different climatic conditions in Spain. Resources, Conservation and Recycling, 175, 105838. DOI:10.1016/j.resconrec.2021.105838

MARTÍNEZ-MUÑOZ, D.; MARTÍ, J.V.; YEPES, V. (2021). Comparative life cycle analysis of concrete and composite bridges varying steel recycling ratio. Materials, 14(15):4218. DOI:10.3390/ma14154218

MARTÍNEZ-MUÑOZ, D.; MARTÍ, J.V.; GARCÍA, J.; YEPES, V. (2021). Embodied energy optimization of buttressed earth-retaining walls with hybrid simulated annealing. Applied Sciences, 11(4):1800. DOI:10.3390/app11041800

NAVARRO, I.J.; PENADÉS-PLÀ, V.; MARTÍNEZ-MUÑOZ, D.; REMPLING, R.; YEPES, V. (2020). Life cycle sustainability assessment for multi-criteria decision making in bridge design: A review. Journal of Civil Engineering and Management, 26(7):690-704. DOI:10.3846/jcem.2020.13599.

MARTÍNEZ-MUÑOZ, D.; MARTÍ, J.V.; YEPES, V. (2020). Steel-concrete composite bridges: design, life cycle assessment, maintenance and decision making. Advances in Civil Engineering, 2020:8823370. DOI:10.1155/2020/8823370

PENADÉS-PLÀ, V.; MARTÍNEZ-MUÑOZ, D.; GARCÍA-SEGURA, T.; NAVARRO, I.J.; YEPES, V. (2020). Environmental and social impact assessment of optimized post-tensioned concrete road bridges. Sustainability, 12(10), 4265. DOI:10.3390/su12104265

YEPES, V.; DASÍ-GIL, M.; MARTÍNEZ-MUÑOZ, D.; LÓPEZ-DESFILÍS, V.J.; MARTÍ, J.V. (2019). Heuristic techniques for the design of steel-concrete composite pedestrian bridges. Applied Sciences, 9(16), 3253; DOI:10.3390/app9163253

Limitaciones de los métodos de toma de decisiones basados en procesos de jerarquía analítica AHP

Figura 1. Ejemplo de estructura jerárquica AHP

Cuando el profesor Thomas Saaty dió a conocer el método AHP (Analytic Hierarchy Process) en la década de los 80, ya se dio cuenta de que este procedimiento presentaba algunas limitaciones que debía solucionar más adelante. En el año 1996 presentó el modelo ANP (Analytic Network Process) como una generalización de AHP. Este modelo permitió incluir relaciones de interdependencia y realimentación entre elementos del sistema (criterios y alternativas).

En este artículo nos vamos a centrar en algunas limitaciones de AHP que conviene tener en cuenta al tomar decisiones. Este aspecto no es menor, puesto que existen modelos basados en AHP que pueden verse arrastrados por alguna de estas limitaciones.

No obstante, no todo son inconvenientes, ni mucho menos. El profesor José María Moreno ya nos advierte, tal y como se desprende del artículo que os dejo al final de este post, que en este momento no se ha podido probar la supremacía de ningún método o escuela de pensamiento en lo que se refiere al paradigma de la toma de decisión multicriterio. De hecho, AHP ha basado su éxito en trasladar las percepciones humanas a valores numéricos evaluados en una escala de prioridades que permiten sintentizar lo tangible y lo intangible, lo objetivo y lo subjetivo, e incluso lo racional y lo emocional. Además, constituye un procedimiento fácil de utilizar, aplicable a numerosas situaciones reales donde se trata de elegir una alternativa, y donde se puede agregar la decisión individual y la de grupo. Y no menos importante, el AHP es una de las pocas técnicas multicriterio que ofrece una axiomática teórica. Pero veamos ahora en algunos de los inconvenientes de AHP que habrá que valorar siempre que usemos este método o algún otro basado en él.

El principal problema que presenta AHP es que, de forma habitual, existen relaciones de interdependencia y realimentación entre los distintos criterios, subcriterios o alternativas (Figura 2). AHP es unidireccional, siendo las relaciones entre los distintos elementos de abajo hacia arriba, lo cual puede suponer una simplificación demasiado fuerte de la realidad. La condición de independencia y jerarquía que subyace en AHP es necesaria para que quien toma las decisiones tenga una función de valor aditiva. De hecho, AHP se apoya en los axiomas de reciprocidad, homogeneidad y síntesis. Pues este último axioma, que implica que los juicios acerca de las prioridades de los elementos en una jerarquía no dependen de los del nivel más bajo, puede rebatirse cuando existe dependencia de la importancia de un objetivo con el nivel inferior.

Veamos un ejemplo concreto. Si se está analizando la sostenibilidad económica, ambiental y social de una estructura de hormigón, uno de los subcriterios económicos puede ser el coste de la estructura y otro subcriterio ambiental puede ser el consumo de recursos, por ejemplo, la cantidad utilizada de hormigón o de acero. Es evidente que el coste depende de la cantidad de recursos consumidos. Este es un ejemplo muy sencillo, pero en el mundo real, las interdependencias pueden ser sutiles o difíciles de ver a priori. No es fácil, en situaciones normales, encontrar criterios y subcriterios que sean independientes unos de otros.

Figura 2. Relación entre elementos en ANP en la estructura jerárquica AHP (adaptado de Aznar, 2012)

Una de las objeciones recibidas por el método es que si la jerarquía en AHP es incompleta, pueden distorsionarse los pesos. Otro problema adicional tiene que ver con el número de criterios en cada nivel y con su ponderación relativa. Supongamos, por ejemplo que hay dos criterios en el primer nivel y que sus pesos son del 75% en uno y del 25% en el otro. Esta ponderación ya condiciona de forma drástica las ponderaciones de todas las variables que cuelgan de ellas. De esta manera, prácticamente se está anulando el interés de los subcriterios que dependen jerárquicamente de aquel menos ponderado en el primer nivel. El profesor Aznar (2012) ilustra, con ejemplos concretos, cómo el uso de ANP, frente a AHP, provoca cambios significativos en la valoración final de cada una de las alternativas.

También hay que indicar que la escala de nueve puntos de Saaty (los valores siempre entre 1 y 9) es arbitraria para medir las preferencias de los decisores. Esta escala puede plantear, por ejemplo, el siguiente problema: Si una alternativa A es 5 veces más importante que la alternativa B y esta a su vez es 5 veces más importante que la alternativa C, se produce un problema serio, ya que AHP no puede manejar el hecho de que la alternativa A es 25 veces más importante que la alternativa C. Esta deficiencia se visualiza en la Figura 3. Se puede ver cómo la alternativa círculo rojo es mejor al resto con la escala de Saaty: 5 para el triángulo, 7 para el rombo y 9 para el cuadrado. Si comparamos el triángulo verde con el resto, debería ser: 3 para el rombo y 5 para el cuadrado. Del mismo modo, el rombo presenta una valoración de 3 respecto al cuadrado. Con esta matriz pareada, el ratio de consistencia es válido. Sin embargo, si se reajustan las valoraciones dividiendo por dos las comparaciones del triángulo, rombo y cuadrado, el ratio de consistencia baja significativamente. En ese caso, los autovectores han cambiado, aunque se mantienen las prioridades.

Figura 3. Ratio de consistencia en función de las comparaciones pareadas. Elaboración propia

Pero aquí no terminan los inconvenientes. Como contrapartida a la simplicidad, AHP no tiene en cuenta la incerteza asociada a representar la opinión en la forma de un número. Además, si se agrega durante el proceso otra alternativa, las clasificaciones de las alternativas originales pueden cambiar, lo cual rigidiza el método. Por otra parte, si se incrementa el número de alternativas o criterios, se puede llegar a la inconsistencia de la matriz de comparaciones pareadas. Asimismo, en el método es muy laborioso si se incrementa el número de alternativas o criterios.

Un inconveniente adicional de AHP es la normalización de las matrices de preferencias, transformando las valoraciones planteadas en utilidades definidas en la escala (0,1) mediante la obtención del vector propio de las mismas. Esto solo es estrictamente válido si los juicios volcados en la matriz son perfectamente consistentes. En caso contrario, puede ser complicada la interpretación.

Sin embargo, los problemas con AHP se agudizan cuando aparece una situación de conflicto en la que existe una mayor o menor oposición en los intereses de los decisores y, además, las decisiones de cada decisor dependen de las que tomen los demás en la búsqueda de sus propios intereses. En este caso, la teoría de juegos o juegos de estrategia sería la forma más razonable de abordar el problema.

En apretada síntesis, estas reflexiones vienen a cuento de que, muchas veces, estamos utilizando métodos, incluso recogidas alguna normativa legal, donde se pretende dar cuerpo de ley a un conjunto de criterios para evaluar algún aspecto de especial interés. Es el caso del método AHP empleado, por ejemplo, como parte de otros como MIVES, que han dado lugar, a un índice de contribución de la estructura a la sostenibilidad (Anejo 2 del Código Estructural). Con todo, y para tranquilidad de muchos, la teoría AHP, si bien presenta ciertos problemas como los expuestos, parece conservar su condición de ser el método de toma de decisión más conocido y empleado de los métodos multicriterio.

También, por su interés, os dejo el artículo de José Luis Zanazzi sobre las críticas recibidas por AHP y su análisis.

Descargar (PDF, 223KB)

Pero no todo van a ser noticias negativas en relación con el AHP. Os dejo, a continuación, el artículo del profesor José María Moreno donde explica el método AHP.

Descargar (PDF, 343KB)

Referencias:

AZNAR, J.; GUIJARRO, F. (2012). Nuevos métodos de valoración: modelos multicriterio. Editorial Universitat Politècnica de València.

SAATY, T.L. (1980). The Analytic Hierarchy Process: Planning, Priority Setting, Resource Allocation, McGraw-Hill.

Licencia de Creative Commons
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.