Acaban de publicar un artículo nuestro en Results in Engineering, una de las revistas de mayor impacto científico, ubicada en el primer decil del JCR. Este trabajo trata sobre un sistema avanzado para el seguimiento de la salud estructural (SHM, por sus siglas en inglés) y la optimización de puentes de gran envergadura y estáticamente indeterminados (hiperestáticos).
La investigación se enmarca en el proyecto RESILIFE, que dirijo como investigador principal en la Universitat Politècnica de València. Además, muestra la internacionalización de nuestro grupo de investigación, en este caso, con China. A continuación, se presenta un resumen del trabajo y de la información de contexto.
El problema central que se aborda en este trabajo es la insuficiencia de los métodos de supervisión tradicionales, ya que no permiten una vigilancia continua, en tiempo real y a distancia, crucial para garantizar la seguridad, la longevidad y el mantenimiento rentable de estas complejas infraestructuras.
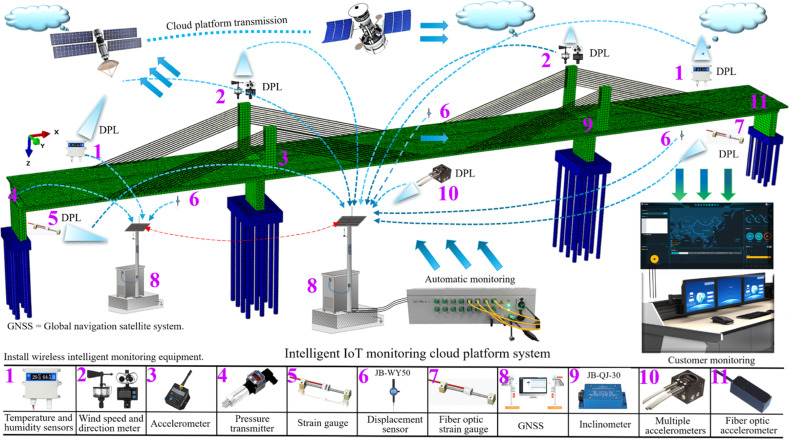
La solución propuesta es una plataforma inteligente en la nube para el control y la alerta temprana que integra la informática, la ingeniería de comunicaciones, el control y la automatización y la mecánica de ingeniería. Este sistema combina los datos de supervisión en tiempo real, obtenidos mediante la tecnología de Internet de las Cosas (IoT), con modelos de elementos finitos (FEM) para evaluar con precisión el estado de la estructura.
Su eficacia se demostró mediante un estudio de caso del Puente del Río Amarillo en China (LZYB). El análisis de los datos de seguimiento y las simulaciones por elementos finitos revelaron que el diseño original del puente era excesivamente conservador, ya que la deflexión vertical real bajo cargas operativas representaba entre el 26,5 % y el 33,9 % del valor predicho en el diseño.
Con base en este hallazgo, se optimizó el diseño de la viga principal del puente, lo que permitió reducir el volumen de hormigón de la losa de fondo en un 15 %. Un análisis posterior del ciclo de vida (LCA) cuantificó los beneficios de esta optimización, que incluyen una reducción de 2009,65 toneladas de emisiones de CO₂ y un ahorro económico de 2 694 189,55 CNY, sin comprometer la seguridad ni el rendimiento estructural. Este enfoque representa un nuevo paradigma para el mantenimiento seguro, económico y sostenible de infraestructuras críticas.
1. Introducción y desafíos de la auscultación estructural.
Los puentes de gran envergadura y estáticamente indeterminados están sometidos a múltiples factores que pueden afectar a su integridad, como la respuesta dinámica de la estructura y el daño por fatiga acumulada debido a la interacción de cargas múltiples y condiciones ambientales complejas. Las microfisuras internas pueden propagarse hasta convertirse en fisuras macroscópicas y provocar la inestabilidad y el fallo de la estructura.
1.1. Limitaciones de los métodos tradicionales.
- Inspección visual: los métodos iniciales, basados en la inspección visual realizada por personal cualificado para detectar defectos superficiales, como las grietas por fatiga, son imprecisos y propensos a errores.
- Supervisión de la salud estructural (SHM) convencional: ha mejorado la precisión, pero enfrenta desafíos como la falta de sensores adecuados para el monitoreo autónomo a largo plazo y de algoritmos eficaces para predecir y diagnosticar daños locales por fatiga.
- Enfoques basados en algoritmos: existen dos métodos principales: los basados en modelos, que utilizan un modelo de elementos finitos preciso, pero que consumen mucho tiempo, y los basados en datos, que analizan series temporales continuas, pero que pueden verse limitados por las bajas tasas de transmisión de datos de las redes inalámbricas.
El estudio aborda estas limitaciones combinando las ventajas de ambos enfoques e integrando algoritmos innovadores de alta eficiencia para avanzar en la monitorización continua de la salud estructural.
2. Marco teórico e innovación del sistema.
El trabajo establece un modelo teórico complejo y una plataforma inteligente que integra múltiples disciplinas para superar las barreras técnicas del seguimiento tradicional.
2.1. Puntos clave de la innovación.
- Modelo interdisciplinario: se desarrolló un modelo teórico modal complejo, multifactorial y de múltiples fuentes que combina la ciencia de la computación, la ingeniería de comunicaciones, el control y la automatización y la mecánica de ingeniería. Este modelo analiza el impacto de múltiples factores en las estructuras de los puentes y permite realizar un seguimiento de alertas tempranas en una plataforma en la nube.
- Supervisión basada en IoT: se adopta un monitoreo en línea, automatizado y en tiempo real basado en el Internet de las cosas (IoT). De este modo, se soluciona la incapacidad de la tecnología tradicional para lograr un seguimiento espaciotemporal continuo y a gran distancia, y se transforma el seguimiento de un «basado en puntos, indirecto y de ajuste de curvas» a otro «espacial, directo y continuo».
- Sistema de alerta temprana: proporciona un modelo eficaz de control y de alerta temprana para diversos tipos de deterioro, como grietas, deformaciones, envejecimiento y vibración dinámica. Valida la viabilidad de la estructura en términos de integridad, seguridad, durabilidad y control de la resistencia.
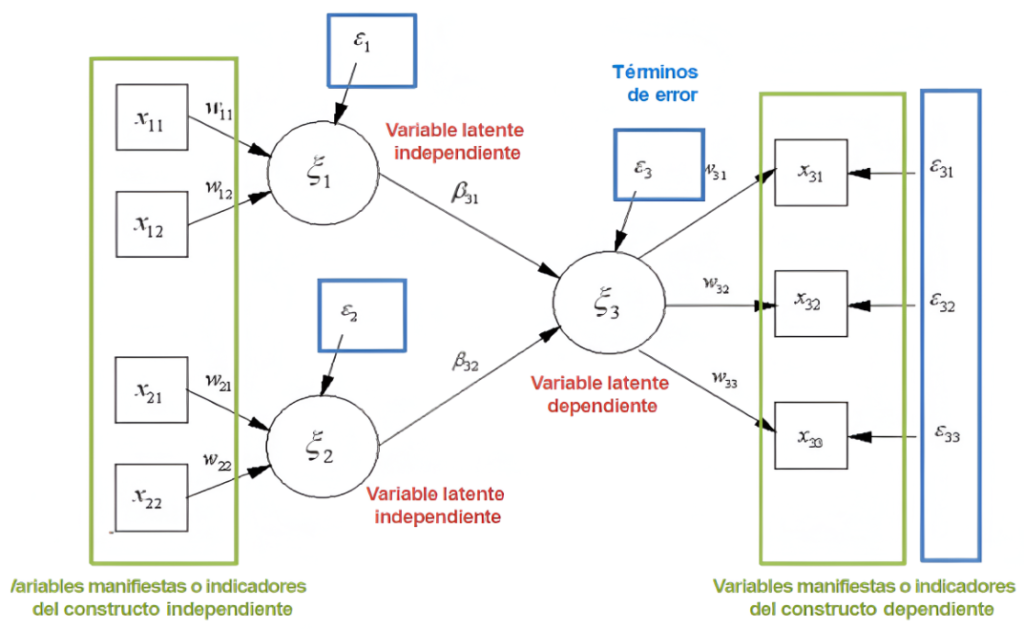
2.2. Componentes del modelo teórico.
El modelo matemático integra varios análisis para evaluar el estado de la estructura:
- Daño por fatiga estructural: utiliza un modelo de daño por fatiga acumulativa no lineal para analizar la propagación de las fisuras y la degradación continua del módulo de elasticidad del hormigón.
- Daño por fatiga del acero: se considera que la vida útil del puente está determinada principalmente por la fatiga de las barras de acero. El modelo calcula la profundidad crítica de la fisura y la tensión residual del acero.
- Efecto de cargas múltiples: se aplica un modelo de mezcla gaussiana para analizar los datos de monitorización, que presentan una distribución de picos múltiples, y se calcula la deflexión total considerando la carga viva, la tensión térmica, la pérdida de pretensado y la retracción y la fluencia del hormigón.
- Acoplamiento vehículo-puente: Construye una ecuación de un sistema de movimiento acoplado para analizar las interacciones mecánicas entre los vehículos y el puente.
- Optimización dinámica estructural: utiliza un modelo matemático basado en la función lagrangiana para realizar un diseño de optimización dinámica con un ritmo de convergencia rápido.
3. Estudio de caso: el puente del río Amarillo (LZYB)
La metodología se aplicó a esta estructura atirantada, con un vano principal de 360 metros, ubicada en China.
3.1. Descripción del puente y sistema de control
- Especificaciones: El LZYB es un puente extragrande para autopista de cuatro carriles con torres romboidales de hormigón armado (C50), una altura de torre de hasta 151 metros y cables atirantados de haces de alambre de acero paralelos galvanizados.
- Sistema de monitorización: se instalaron 374 dispositivos de 10 tipos diferentes, incluidos sensores de temperatura y de humedad, acelerómetros, extensómetros y sensores de fibra óptica, entre otros. Estos dispositivos se ubicaron en puntos críticos de momento flector y de fuerza cortante, determinados mediante principios de mecánica y el modelo FEM. Los datos se transmiten en tiempo real a una plataforma en la nube basada en internet de las cosas (IoT, por sus siglas en inglés) para su análisis y alerta temprana.
| Número | Elementos de control | Indicadores de alerta | Método de adquisición |
| 1 | Análisis del modelo de vehículo | Identificación de carga nominal (nº de ejes, longitud) | Videovigilancia |
| 2 | Análisis del flujo de tráfico | Autopista de 4 carriles (ADT 2 500-55 000 vehículos) | Videovigilancia; captura de video |
| 3 | Análisis de sobrepeso | Límite de 49 toneladas (se detectaron 82.5; 110 ton) | Control dinámico de pesaje |
| 4 | Análisis de exceso de velocidad | Límite de 80 km/h | Control de flujo con exceso de velocidad |
| 5 | Control de temperatura ambiental | Intervalo de control: -15 ~ 39 °C | Sensor de fibra óptica de temperatura |
| 6 | Control de humedad ambiental | 6,5 % ~ 98 % (torre principal); prevenir corrosión | Sensor de fibra óptica de humedad |
| 7 | Control de carga de viento | Velocidad del viento < 25,8 m/s | Anemómetro |
| 8 | Control de carga sísmica | E1 < 0,20g | Instrumento de medición de movimiento del suelo |
| 9 | Control de respuesta estructural | Frecuencia natural inferior al valor teórico calculado | Equipo de monitorización de fibra óptica |
3.2. Análisis de los datos de monitorización en tiempo real (abril-julio).
- Cargas de tráfico: se observó un crecimiento mensual significativo en el volumen total de tráfico, en el número de vehículos con sobrepeso y en el de vehículos que circulaban a exceso de velocidad. El tráfico medio diario osciló entre 7319 y 14 431 vehículos, con picos en junio y julio.
- Respuesta estructural (deformación): la respuesta de deformación bajo cargas de vehículos mostró una distribución de picos múltiples. El análisis identificó que dicha respuesta se concentraba en la sección de 3.50 L a 5.50 L del lado oeste.
- Acoplamiento temperatura-deflexión: se halló una fuerte correlación positiva entre la temperatura ambiental y la deflexión de la viga principal (R² = 0,6953). La deflexión máxima registrada fue de 628,9 mm. El análisis identificó las zonas de la viga principal en las que la influencia de la temperatura sobre la deflexión era más marcada.
3.3. Acoplamiento y análisis mediante el modelo de elementos finitos (MEF).
Se creó un modelo 3D del LZYB en Abaqus/CAE 2021 para simular su comportamiento bajo cargas de diseño. Los resultados de la simulación fueron los siguientes:
- Energía: la energía máxima se concentró en la losa de fondo de la viga principal, entre los vanos 2 y 3.
- Deformación: la máxima deformación (0,004813 µε) se observó en la parte media de los cables atirantados.
- Tensión: La tensión máxima (991,175 MPa) se localizó también en los cables atirantados, concretamente en el cable 3-1.
- Desplazamiento: El desplazamiento vertical máximo calculado fue de 0,002267 metros en el centro del vano principal (sección 6L/12 de la viga).
4. Discusión: optimización y evaluación de la sostenibilidad.
La comparación entre los datos de supervisión en tiempo real y los resultados del FEM sirvió de base para optimizar el diseño.
4.1. Redundancia estructural identificada.
El análisis comparativo reveló una discrepancia significativa: la deflexión vertical global del puente durante su funcionamiento (entre 0,0021 y 0,5944 m) representaba entre el 26,50 % y el 33,90 % del valor máximo predicho por el modelo FEM con cargas de diseño (hasta 2,2434 m). Este hecho indica que el diseño estructural es significativamente conservador o «redundante».
4.2. Optimización del diseño de la viga principal.
Aprovechando la redundancia identificada, se llevó a cabo un proceso de optimización del diseño acoplado de la viga principal. Se analizó el impacto de reducir el volumen de hormigón de la viga de forma iterativa.
Resultado de la optimización: se determinó que era posible reducir el volumen de hormigón de la losa de fondo de la viga principal en un 15 % (es decir, reducir su espesor a 70 mm) sin comprometer el cumplimiento de los requisitos de rendimiento bajo las cargas de diseño originales.
4.3. Evaluación del ciclo de vida (LCA) y de los beneficios.
Se realizó una evaluación del ciclo de vida (LCA) para cuantificar los beneficios ambientales y económicos del diseño optimizado.
Beneficios ambientales y económicos: la reducción del 15 % del hormigón utilizado en la viga principal se traduce en un ahorro significativo a lo largo de todo el ciclo de vida del proyecto.
| Indicador de evaluación | Reducción |
| Calentamiento global (GWP100a) | 2009,65 toneladas de CO2 eq. |
| Acidificación (AP) | 8,86 toneladas de SO2 eq. |
| Eutrofización (FEP) | 7,12 toneladas de PO4 eq. |
| Polvo en suspensión (PMFP) | 79,63 toneladas |
| Ahorro económico (coste de material) | 2 694 189,55 CNY |
5. Conclusiones y hallazgos clave
La investigación demuestra con éxito la viabilidad de un sistema inteligente de supervisión en la nube, acoplado a un modelado FEM, para analizar la seguridad y optimizar el diseño de puentes de gran envergadura.
Resultados clave:
- Fallo de cables: el fallo de los cables es un factor crítico para la estabilidad de los puentes atirantados y debe ser un objetivo principal del seguimiento.
- Ubicación de la tensión máxima: la tensión más alta se concentra en los cables más largos (en este caso, el cable n.º 10), específicamente en la zona situada a menos de 2 metros de la parte superior de la torre principal.
- Diseño del sistema de monitorización subóptimo: el diseño actual de los puntos de control resulta ineficiente. No hay sensores en la parte superior de la torre, donde la tensión es máxima, mientras que hay demasiados en la viga principal.
- Enfoque del mantenimiento: el mantenimiento rutinario de los cables atirantados debe centrarse en las zonas de conexión de la parte superior de la torre y de la viga principal.
Innovación y limitaciones: La principal innovación del estudio consiste en aplicar de manera sistemática datos medidos y el modelado FEM 3D para resolver problemas de seguridad y optimización en puentes complejos. Esto ofrece un ejemplo práctico de supervisión en tiempo real y de análisis de la solidez de los datos. Una limitación reconocida es la falta de un estudio en profundidad sobre los efectos destructivos de las sobrecargas de peso y de velocidad, lo que sugiere una línea de investigación para el futuro.
Referencia:
ZHOU, Z.; ZHAO, Z.; ALCALÁ, J.; YEPES, V. (2025). Intelligent operation monitoring and finite element coupled identification of hyperstatic structures. Results in Engineering, 27, 106990. DOI:10.1016/j.rineng.2025.106990
Os dejo una conversación en la que podéis escuchar las ideas más interesantes de este trabajo.
En este vídeo se resumen las ideas más importantes.
Os he dejado una presentación que resume también lo más importante.
Os dejo el artículo completo, ya que está publicado en formato abierto.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.