Las rotopalas, conocidas en inglés como Bucket Wheel Excavators (BWE), son máquinas de producción continua que integran las funciones de arranque, carga y transporte del material sin interrupciones. Están especialmente diseñadas para excavar materiales de fácil manipulación, como arenas, gravas, margas, arcillas o lignito. Su funcionamiento continuo las hace ideales para explotaciones mineras a cielo abierto, donde se requiere una alta eficiencia operativa en procesos prolongados y repetitivos.
El origen de estas imponentes máquinas se remonta a 1881, en Estados Unidos, cuando se construyó el primer equipo accionado por vapor. Sin embargo, no fue hasta 1916 en Alemania cuando se produjo su verdadero desarrollo industrial, al aplicarse en la explotación de lignito pardo. A partir de la década de 1950, las rotopalas experimentaron una notable evolución técnica, con modelos de mayor capacidad que respondían a las crecientes necesidades de producción. En la actualidad, estas máquinas pueden mover volúmenes superiores a los 254 000 m³ de material, lo que da una idea de su gran capacidad. En comparación, los Bucket Chain Excavators (BCE), aunque útiles en ciertas aplicaciones, apenas superan los 14 000 m³ y se emplean principalmente para retirar recubrimientos.
El diseño de las rotopalas se clasifica según la relación entre la longitud del brazo del rodete (L) y el diámetro del rodete (D). De este modo, se distinguen los modelos compactos (L/D = 2), semicompactos (L/D = 3) y convencionales (L/D = 4). Las compactas presentan varias ventajas significativas: una inversión inicial un 20 % inferior a la de las convencionales, menor peso, mayor estabilidad y tiempos de entrega más reducidos. Sin embargo, su diseño, limitado a dos orugas, restringe su tamaño máximo a 1600 toneladas, lo que implica una capacidad máxima de producción de 7500 m³/h y un brazo más corto que reduce su alcance operativo. Esta clasificación está normalizada por la norma DIN 22266, que define un sistema de denominación mediante letras que representan distintas características del equipo, como, por ejemplo, el tipo de tren de rodaje o la capacidad de los cangilones.

Una rotopala está formada por múltiples sistemas clave que permiten su funcionamiento. El tren de rodaje puede montarse sobre vías o, lo que es más habitual en minería a cielo abierto, sobre orugas. La configuración de estas últimas (dos, tres, cuatro, tres dobles o seis dobles) depende del peso de la máquina y de la capacidad portante del terreno. Cada oruga incorpora un bastidor, una rueda motriz o guía elevada, rodillos de sustentación y zapatas. La corona de giro permite orientar el brazo del rodete, cuya longitud influye directamente en la altura máxima de excavación, la anchura del bloque que se va a extraer y la selectividad del corte. El rodete es el elemento encargado de arrancar el material y su diseño depende de las propiedades geomecánicas del macizo rocoso, la resistencia del material y la producción horaria deseada. Su diámetro oscila entre 2,5 y 22 metros, y su capacidad productiva está entre 200 y 19 000 m³/h. Además, cada tonelada adicional en el peso del rodete implica una carga extra de 400 toneladas sobre la estructura de la máquina.
Existen varios tipos de rodete. El tipo celular, muy habitual en los parques de homogeneización, emplea una placa de caída con forma de arco que crea una célula para conducir el material hacia la cinta lateral. El tipo no celular se caracteriza por tener cangilones insertados en un espacio anular, con un cierre radial que permite aumentar la capacidad del cangilón en un 50 %. Por último, el tipo semicircular tiene un cierre inferior con planos inclinados llamados semicelulares y una vertedera fija. Los cangilones pueden tener un respaldo cerrado, que es ideal para materiales adhesivos como las arcillas duras (tipo «caparazón de tortuga»), o un respaldo de cadenas, que es más adecuado para materiales blandos, húmedos o pegajosos. Los elementos de corte, como dientes, cuchillas u orejetas angulares, son determinantes para la eficiencia de la excavación y deben ser fácilmente sustituibles, resistentes a la abrasión y al impacto. En materiales duros, pueden incorporarse precortadores que fragmentan previamente el material, aunque esto puede generar sobrecargas y vibraciones no deseadas.

El sistema de izado permite posicionar el rodete a la altura de operación deseada y realizar descensos o ascensos rápidos mediante cilindros hidráulicos o cables de acero. Por otro lado, la descarga del material excavado se realiza mediante sistemas como puentes de conexión, brazos de descarga o cintas transportadoras, lo que otorga gran flexibilidad al sistema.
El dimensionamiento de una rotopala debe tener en cuenta múltiples factores técnicos. El diámetro del rodete se selecciona en función de la capacidad nominal requerida y de las propiedades del material, procurando elegir el diámetro más pequeño posible que cumpla los objetivos de producción, ya que un rodete de mayor tamaño incrementa el peso y complica la estática de la máquina. La capacidad nominal (Q) distingue entre la producción teórica o de diseño (Qt) y la producción real, que se ve afectada por factores como el grado de llenado de los cangilones y las paradas por mantenimiento o averías. La producción teórica se calcula mediante la fórmula Qt = Qa / (F · horas/día · días/año), donde F es un factor de campo que incluye la eficiencia y las constantes operativas. La producción de material suelto se determina aplicando el esponjamiento del material, que normalmente se sitúa entre 1,3 y 1,6, o mediante la fórmula Qts = I * s * 60, donde I es la capacidad del cazo y s el número de descargas por minuto.
El tipo de material que se va a excavar influye en la velocidad de corte, el número de cangilones, el diámetro del rodete y la inclinación del brazo. La velocidad de corte (Vc) se calcula como Vc = ω · D / 2 y suele estar entre 2 y 3,5 m/s, debiendo mantenerse por encima de la velocidad crítica (Vcri = 2,22 · D). El número de cangilones (Z) depende del material: las rocas blandas requieren pocos cangilones grandes, mientras que las rocas duras exigen muchos cangilones pequeños. Como estimación, se puede considerar Z = 4D. La frecuencia de descarga (s) se obtiene mediante la fórmula s = (Vc · Z) / (π · D) · 60, y la capacidad de los cangilones (V) mediante V = (Qts · 60) / (s · 1,25). Las potencias necesarias para la excavación, la aceleración, la elevación y el sistema completo deben calcularse en función de la producción deseada, el tipo de material y el diseño mecánico del equipo.
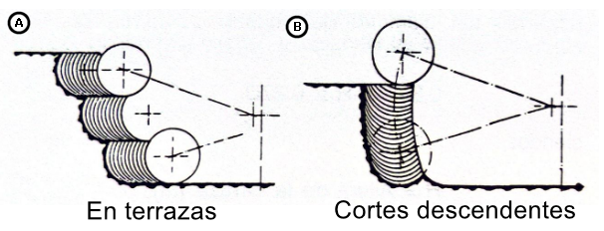
Durante la operación, el rodete gira mientras el brazo se mueve y el corte más eficiente se produce cuando el brazo está perpendicular al frente de trabajo (ángulo α = 0°). El avance puede realizarse en terrazas, donde el rodete desciende escalonadamente tras cada pasada, o en cortes descendentes, bajando con cada inversión del giro del brazo. Existen diversas variantes operativas, como la excavación en bloque lleno, la más común en la actualidad gracias a la movilidad sobre orugas, la excavación en frente largo, en la que la máquina avanza en paralelo al frente, y la excavación en bloque lateral, que es una adaptación del sistema anterior. También es posible excavar por debajo del nivel de las orugas, lo que permite trabajar con bancos de mayor altura con respecto a la posición del tren de rodaje.
Entre las múltiples ventajas de las rotopalas, destacan su capacidad de excavación continua, su bajo consumo energético (hasta un 70 % menos que los sistemas de cables), la ausencia de impactos durante la carga, su gran radio de vertido y la posibilidad de operar tanto por encima como por debajo del nivel del terreno. Además, pueden trabajar en bancos de distintas alturas, generar taludes estables, entregar material fácilmente transportable por cinta y permitir una gran selectividad en la excavación. También pueden diseñarse para ejercer una baja presión sobre el terreno, lo que resulta clave en zonas con baja capacidad portante.
Sin embargo, no todo son ventajas. Las rotopalas requieren un mantenimiento complejo y frecuente, no son flexibles ante cambios en la geometría o tectónica del yacimiento y no sirven para excavar materiales compactos o muy abrasivos. Además, su rendimiento global depende de la disponibilidad de todos los elementos en serie que componen el sistema, lo que introduce una fuerte interdependencia operativa. Por último, su adquisición e instalación suponen una inversión inicial muy elevada, lo que limita su adopción a proyectos a gran escala y a largo plazo.
En resumen, las rotopalas son una solución de ingeniería impresionante para grandes operaciones mineras, ya que combinan eficiencia, potencia y continuidad operativa. No obstante, no son la herramienta adecuada para todos los contextos y, en las condiciones apropiadas, su rendimiento y productividad son difíciles de igualar.
Os dejo algunos vídeos que espero os interesen:
Referencias:
GÓMEZ DE LAS HERAS, J.; MANGLANO, S.; TOLEDO, J.; LÓPEZ-JIMENO, C.; LÓPEZ-JIMENO, E. (1995). Manual de arranque, carga y transporte en minería a cielo abierto. Instituto Geológico y Minero de España, Madrid, 604 pp.
MARTÍNEZ-PAGÁN, P. (2025). Rotopalas. Apuntes 4º curso GIRME. Universidad Politécnica de Cartagena.
YEPES, V. (1995). Maquinaria de movimiento de tierras. Servicio de Publicaciones de la Universidad Politécnica de Valencia. SP.UPV-264. 144 pp.
YEPES, V. (1997). Equipos de movimiento de tierras y compactación. Problemas resueltos. Colección Libro Docente n.º 97.439. Ed. Universitat Politècnica de València. 256 pág. Depósito Legal: V-4598-1997. ISBN: 84-7721-551-0.
YEPES, V. (2022). Gestión de costes y producción de maquinaria de construcción. Colección Manual de Referencia, serie Ingeniería Civil. Editorial Universitat Politècnica de València, 243 pp. Ref. 442. ISBN: 978-84-1396-046-3
YEPES, V. (2023). Maquinaria y procedimientos de construcción. Problemas resueltos. Colección Académica. Editorial Universitat Politècnica de València, 562 pp. Ref. 376. ISBN 978-84-1396-174-3
Curso:
Curso de gestión de costes y producción de la maquinaria empleada en la construcción

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.