geotecnia – El blog de Víctor Yepes

Efectos de las inundaciones en las estructuras de las edificaciones

Figura 1. Efectos de la DANA en Valencia. https://www.diariodesevilla.es/sociedad/catastrofe-inundaciones-valencia-directo_10_2002684877.html

Para comprender los efectos de las inundaciones en las estructuras de las edificaciones y cómo responder ante ellas, es fundamental entender tanto los factores que incrementan la vulnerabilidad de los edificios como las acciones preventivas y correctivas necesarias. Las inundaciones pueden afectar seriamente a las estructuras, dependiendo de la magnitud de las aguas, su salinidad, la saturación del suelo y la calidad de los materiales y prácticas constructivas empleados. La identificación de estos daños requiere evaluaciones técnicas detalladas y precisas. Este conocimiento es útil tanto para los propietarios, los técnicos y el personal de emergencias que deben tomar decisiones rápidas y bien fundamentadas en situaciones críticas.

1. Efectos de las inundaciones en la estructura de las edificaciones

Las inundaciones suponen una amenaza significativa para la integridad de los edificios y pueden afectar a la estructura de diversas maneras. Estos no siempre son visibles de inmediato y pueden empeorar con el tiempo si no se toman medidas correctivas. En las zonas propensas a las inundaciones, los edificios pueden sufrir diversos daños estructurales, como:

Socavación y fallos en la cimentación: La erosión causada por la corriente de agua disminuye la estabilidad de los cimientos. Cuando una inundación causa socavones cerca de una edificación, esto afecta directamente a la capacidad portante de los cimientos, ya que se pierde el soporte horizontal y lateral del suelo. Esto puede causar inclinaciones en las estructuras, grietas en los muros y, en casos extremos, el colapso parcial o total del edificio.
Erosión del suelo y pérdida de capacidad portante: La capacidad del suelo para soportar cargas se ve reducida debido a la erosión, lo que puede llevar al fallo de la cimentación.
Saturación del suelo: La acumulación de agua provoca saturación, lo que aumenta el riesgo de deslizamientos, derrumbes y avalanchas y afecta a la estabilidad del conjunto de cimentación y estructura. El suelo que rodea los cimientos de una edificación, al saturarse con agua, pierde densidad y estabilidad. Este fenómeno es especialmente crítico en áreas cercanas a cuerpos de agua (ríos, lagos o mares), donde el agua puede hacer que el suelo pierda su capacidad de soporte. Esto puede provocar fenómenos como deslizamientos, derrumbes y licuefacción. En casos graves, el terreno bajo la edificación se comporta casi como un líquido, perdiendo su capacidad para soportar el peso de la estructura y poniendo en riesgo su estabilidad.
Pérdida de soporte lateral y horizontal: Al disminuir la capacidad portante del suelo, la estructura pierde los soportes laterales y horizontales, lo que compromete su estabilidad y capacidad de carga.
Deterioro de los muros exteriores: Cuando el nivel de las inundaciones supera el metro de altura, la descompensación de presiones puede provocar fallos en los muros exteriores..
Inestabilidad estructural por impacto de escombros: Los escombros arrastrados por el agua, combinados con la presión hidrostática o hidrodinámica, pueden impactar en elementos estructurales y causar inestabilidad.
Aparición de grietas en muros, losas y columnas: Dependerá de la magnitud de la inundación y podría ocasionar daños que van desde reparables hasta irreparables.
Daños por capilaridad y humedad en las paredes: El fenómeno de capilaridad permite que el agua suba a través de los materiales porosos de los muros, debilitándolos progresivamente. Este problema es más frecuente en estructuras construidas directamente sobre el suelo sin barreras de impermeabilización o sobrecimientos. El agua absorbida por capilaridad puede afectar a la durabilidad y la resistencia de los materiales, provocando grietas y desprendimientos del revestimiento.
Deterioro de materiales de construcción: La exposición al agua contaminada o salina provoca corrosión en los materiales, especialmente en elementos metálicos no protegidos, galvanizados o inoxidables.

Para reducir estos riesgos, las nuevas construcciones en zonas de inundación deben ser diseñadas y construidas con especificaciones a prueba de inundaciones. Estas mejoras en la resistencia estructural no solo reducen el riesgo de fallos, sino que también disminuyen significativamente la probabilidad de víctimas en escenarios de inundación.

2. Problemática: daños y consecuencias

Daños estructurales: Las inundaciones generan múltiples efectos en la estabilidad de los edificios, afectando su integridad estructural. Entre estos daños destacan:
- Presión hidrostática: La acumulación de agua en el perímetro de la edificación ejerce presión horizontal sobre los muros, proporcional al calado de la inundación. Este tipo de presión puede levantar los suelos o cimentación cuando el agua se acumula de un solo lado del edificio. En casos donde el agua ingresa al edificio, esta presión se neutraliza, pero introduce una carga gravitatoria que afecta elementos horizontales como forjados y soleras, pudiendo conducir al colapso de la estructura.
- Presión hidrodinámica: El flujo de agua de un río desbordado puede alcanzar velocidades considerables y generar impactos en los muros, los cuales deben ser diseñados para soportar estas cargas dinámicas.
- Impactos de objetos arrastrados: El agua arrastra escombros, vehículos y mobiliario urbano que impactan contra la edificación, generando daños considerables en sus elementos.
- Durabilidad y corrosión: El agua, especialmente si contiene minerales y sales, puede corroer el acero de refuerzo en estructuras de hormigón, debilitando su capacidad de carga. En materiales como la madera, la humedad reduce significativamente su resistencia estructural. Estos daños son más difíciles de detectar cuando los elementos están cubiertos o enterrados.
- Erosión del material y del terreno: La exposición prolongada al agua, especialmente si el flujo es constante, puede erosionar materiales como ladrillo y bloque, deteriorando el mortero de unión y comprometiendo la estabilidad del edificio. El terreno también se ve afectado, sobre todo en su capacidad de soporte, agravando el riesgo de asentamientos diferenciales en la cimentación.
Daños constructivos y estéticos: Las inundaciones afectan no solo a los elementos estructurales, sino también a los acabados y componentes funcionales de los edificios:
- Daños en cerramientos y tabiques: Los paramentos exteriores e interiores pueden experimentar corrosión en elementos metálicos, pérdida de adhesión en revestimientos y daños en aplacados.
- Pérdida de estabilidad en fachadas y tabiques: Los impactos de objetos arrastrados por el agua o la reducción en las propiedades de los materiales debido a la humedad pueden hacer que las fachadas o tabiques colapsen.
- Daños en pavimentos: La prolongada presencia de agua produce abombamientos y deformaciones en los suelos, especialmente en los pavimentos de madera, causando el levantado de los materiales de agarre.
- Desperfectos estéticos: La humedad genera manchas y decoloración en superficies, mientras que los impactos pueden provocar la rotura de elementos ornamentales.
- Disfunción de instalaciones: Las instalaciones eléctricas, redes de saneamiento, sistemas de agua potable y equipos de ventilación y climatización pueden colapsar o fallar debido a la exposición a la humedad y obstrucción por residuos, lo cual compromete la funcionalidad del edificio.
Daños al contenido: El ingreso de agua en el interior de un edificio provoca, inevitablemente, daños en su contenido, desde pérdidas materiales como aparatos electrónicos, mobiliario y documentos, hasta daños económicos significativos en edificaciones comerciales e industriales. Además, los edificios que almacenan bienes sensibles, como bibliotecas o museos, pueden sufrir daños irreparables en sus colecciones culturales o documentales.
Daños funcionales: Las inundaciones pueden afectar gravemente al funcionamiento de los edificios, especialmente en instalaciones críticas como hospitales o estaciones de bomberos, donde cualquier interrupción implica riesgos adicionales. Esto incluye la interrupción de servicios esenciales que comprometen la capacidad de respuesta en situaciones de crisis, la inactividad prolongada en edificaciones comerciales o industriales que ocasiona pérdidas económicas y la obstrucción de vías de acceso y evacuación, lo que dificulta las operaciones de emergencia y la seguridad de los ocupantes.
Daños relacionados con el entorno: Además de los daños directos a la estructura, las inundaciones pueden afectar a la parcela circundante y a los elementos del entorno inmediato, provocando erosión y desgaste en áreas sin edificación, como jardines o zonas comunes, donde se acumulan sedimentos y residuos que deterioran el terreno, el mobiliario y la vegetación. Asimismo, elementos del entorno, como vehículos o vegetación arrastrada, pueden afectar a la edificación y provocar asientos diferenciales por los desplazamientos del terreno. Finalmente, los residuos y contaminantes de instalaciones industriales o agrícolas arrastrados por el agua pueden afectar tanto al entorno natural como a la propia edificación.
Daños a largo plazo: Además de los daños inmediatos, las inundaciones pueden causar problemas que se manifiestan con el tiempo, como la corrosión en elementos estructurales debido a la humedad residual en materiales como el hormigón, lo que debilita las armaduras de acero y compromete la estructura gradualmente; también pueden surgir problemas de humedad persistente en áreas de difícil acceso, como los forjados sanitarios, donde el agua estancada crea condiciones favorables para el crecimiento de hongos y otros problemas fitosanitarios.

Estos puntos resaltan la complejidad de los efectos de una inundación en las edificaciones y su entorno, subrayando la importancia de contar con medidas preventivas y de rehabilitación efectivas para mitigar las consecuencias.

3. Identificación de los posibles daños en edificaciones debido a inundaciones

Este capítulo detalla los daños que pueden producirse en una edificación cuando ocurre una inundación. Abarca la identificación de puntos vulnerables, la inspección de elementos de valor, y la evaluación de daños en función del nivel de agua.

Identificación e inventario de puntos débiles: La ubicación y el riesgo del edificio son determinantes para identificar sus puntos débiles y reducir la vulnerabilidad ante las inundaciones. Los principales puntos de entrada del agua en las construcciones son los defectos en el mortero de ladrillo o mampostería, que facilitan la infiltración; las grietas en fachadas y juntas estructurales, especialmente en las uniones entre materiales diferentes, como paredes y losas; las ventanas y puertas, donde las fallas en el sellado y el contacto de los marcos permiten filtraciones; y las escaleras y entradas a sótanos, que al estar en niveles inferiores favorecen la acumulación de agua.
Comprobación de estabilidad estructural: Es crucial evaluar la capacidad de resistencia de los elementos estructurales a las fuerzas del agua, ya que las presiones desiguales pueden dañar paredes y pisos. La diferencia en la rapidez de entrada y salida del agua entre el exterior y el interior del edificio puede generar presión adicional, ocasionando daños estructurales importantes en muros y suelos.
Inspección de los elementos de valor del edificio: Realizar un inventario de los elementos importantes en el edificio permite diagnosticar daños potenciales y planificar su aseguramiento. Estos elementos se clasifican en: seres vivos (personas, mascotas y animales en actividades agropecuarias), continente (que abarca la estructura y el equipamiento, como cimientos, muros, sistemas de electricidad, agua y ventilación) y contenido (que varía según el uso del edificio e incluye mobiliario, documentos y materiales peligrosos).
Diagnóstico de daños en función de la altura del agua: El nivel del agua en el edificio influye directamente en el grado de daño. Ejemplos de daños según el nivel son:
- 0 a 0,3 m (debajo del nivel de la planta baja): Posibles erosiones en cimientos, corrosión en elementos metálicos, acumulación de limo, y formación de moho.
- 0,3 a 0,5 m: Saturación de revestimientos de paredes y suelos, problemas de humedad, y daños en puertas internas y externas.
- Más de 0,5 m: Daños estructurales graves debido a la presión del agua, corrosión y fallos generalizados en sistemas eléctricos y sanitarios.

Estos daños muestran la importancia de realizar un diagnóstico exhaustivo para implementar medidas de mitigación eficientes, que garanticen la seguridad estructural del edificio y la protección de sus ocupantes y contenido.

Figura 3. Inventario de puntos de entrada del agua de inundación. Fuente: Preparing for Flood, Interim guidance for improving the flood resistance of domestic and small business properties. Office of the Deputy Prime Minister. 2003. Environment Agency – UK.

4. Factores de vulnerabilidad que agravan los daños por inundaciones

Las características constructivas y de mantenimiento de una edificación influyen en su vulnerabilidad frente a las inundaciones. Algunos factores clave incluyen:

Ausencia de sobrecimiento e impermeabilización: El sobrecimiento es una barrera de 30-50 cm de altura que se coloca en la base de los muros, y su función es proteger contra la humedad que asciende del suelo. La ausencia de este elemento en una construcción permite que el agua entre en contacto directo con las paredes, lo que facilita la absorción de agua por capilaridad. Además del sobrecimiento, la impermeabilización de cimientos y muros de la planta baja es vital para prevenir que el agua dañe las estructuras.
Calidad de los materiales: Cada material de construcción reacciona de manera distinta a la exposición prolongada al agua. La calidad del cemento, la arena y otros materiales utilizados en la construcción de los bloques y los cimientos influye en la resistencia de la edificación frente a las inundaciones. Los materiales de baja calidad se desintegran más rápidamente cuando entran en contacto con el agua. En áreas con edificaciones antiguas de tapial, por ejemplo, estos tienden a disolverse tras un contacto prolongado con el agua, provocando la descomposición de la estructura. El bahareque, compuesto tradicionalmente por madera, cañas y barro, presenta baja resistencia a la humedad y se deteriora rápidamente, con desprendimientos de revestimiento y deformaciones en la estructura de madera o caña, lo que puede causar inclinaciones o incluso el desplome de las viviendas. En el caso de la mampostería, aunque aparenta ser resistente, los bloques de cemento, por su porosidad y la falta de cocción de algunos materiales, son vulnerables al agua. La humedad puede deteriorar las primeras hiladas, debilitar la base y provocar el desplome parcial o total de la estructura, especialmente en zonas donde los bloques son de baja calidad o con una proporción insuficiente de cemento.
Errores en la construcción: En algunas construcciones, se cometen errores técnicos que comprometen la estabilidad de la estructura, especialmente en zonas inundables. Por ejemplo, el uso incorrecto de aparejos en mampostería o la falta de conocimientos técnicos en la ejecución de los cimientos puede resultar en problemas estructurales graves cuando la edificación enfrenta una inundación.

5. Medidas preventivas para minimizar daños en situaciones de inundación

La implementación de medidas preventivas ayuda a minimizar el impacto de las inundaciones en las edificaciones. Estas son algunas acciones recomendadas:

Inspección y mantenimiento regulares: Es crucial que las edificaciones en zonas propensas a inundaciones reciban mantenimiento constante y revisiones estructurales periódicas. Las inspecciones técnicas pueden identificar signos de desgaste o debilidades estructurales antes de que se conviertan en problemas graves. Esto incluye revisar cimientos, paredes y elementos de soporte clave.
Empleo de materiales resistentes al agua: Al construir o rehabilitar una vivienda en una zona propensa a las inundaciones, se recomienda usar materiales menos porosos y resistentes al agua. Asimismo, en áreas vulnerables, se recomienda aplicar revestimientos y pinturas impermeables en paredes y cimientos para evitar la absorción de humedad.
Adecuación del terreno y del sistema de drenaje: El sistema de drenaje del terreno circundante a una edificación es fundamental para evitar que el agua se acumule y afecte a los cimientos. En zonas propensas a las inundaciones, es importante crear canales de drenaje y pendientes que faciliten la salida del agua hacia áreas de menor riesgo.

6. Recomendaciones de emergencia para responder a inundaciones en edificaciones

En caso de inundación, estas son algunas recomendaciones prácticas para garantizar la seguridad de las personas y proteger, en la medida de lo posible, la estructura del edificio:

Inspección inmediata de daños: Una vez que el nivel del agua haya descendido, es fundamental realizar una inspección detallada del edificio para identificar daños visibles y ocultos. Los técnicos deben evaluar los cimientos y la estabilidad de las paredes para identificar signos de debilitamiento estructural que puedan suponer un riesgo.
Secado y limpieza de estructuras: Es crucial crucial eliminar el agua acumulada y permitir que las estructuras afectadas se sequen. El secado evita que la humedad siga dañando los materiales de construcción. Además, se debe limpiar la suciedad y los restos dejados por la inundación, ya que estos pueden acelerar el deterioro de los materiales.
Refuerzo y reparación de cimientos y paredes: Si las inspecciones revelan daños en los cimientos o paredes, es necesario realizar refuerzos inmediatos para evitar colapsos. Los cimientos debilitados pueden reforzarse con elementos estructurales adicionales y las paredes pueden requerir tratamientos impermeabilizantes o refuerzos de mampostería.

Conclusión

Entender los efectos de las inundaciones en las edificaciones es fundamental para aplicar medidas de prevención y reparación efectivas. Estos eventos pueden causar daños severos en la estructura, la estabilidad y el contenido de los edificios, lo que subraya la necesidad de realizar un diagnóstico preciso y de llevar a cabo acciones correctivas. La identificación de las áreas vulnerables, junto con el uso de materiales adecuados y sistemas de drenaje eficientes, es esencial para reducir los riesgos. Asimismo, el mantenimiento regular y una respuesta rápida ante las inundaciones son cruciales para proteger tanto la seguridad de los ocupantes como la integridad del edificio. La implementación de técnicas constructivas apropiadas mejora la resistencia de las estructuras frente a estos desastres.

A continuación, dejo algunos documentos que creo que pueden ser de interés.

Descargar (PDF, 24.19MB)

Descargar (PDF, 50.33MB)

Descargar (PDF, 1.26MB)

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Técnica innovadora optimiza estructuras de hormigón y reduce emisiones de CO₂ al considerar la interacción suelo-estructura

El artículo científico, titulado «Metamodel-assisted meta-heuristic design optimization of reinforced concrete frame structures considering soil-structure interaction» y publicado recientemente en Engineering Structures, una de las revistas de mayor impacto en ingeniería civil, aborda un desafío clave en la ingeniería estructural: cómo optimizar el diseño de estructuras de hormigón armado para minimizar su impacto ambiental, con especial atención a la reducción de las emisiones de CO₂.

Esta investigación es el resultado de una colaboración internacional realizada en el marco de los proyectos HYDELIFE y RESILIFE, cuyo investigador principal es Víctor Yepes, y es fruto de una colaboración internacional entre investigadores de Cuba, Brasil y España.

Contexto de la investigación

La optimización estructural ha sido ampliamente explorada en las últimas décadas debido a la creciente necesidad de reducir los costes de construcción y el uso de materiales, todo ello mientras se minimiza el impacto ambiental. En el caso de las estructuras de hormigón armado, que son esenciales en la construcción de edificios y obras de infraestructura, optimizar su diseño conlleva implicaciones significativas en cuanto al ahorro de recursos y la reducción de las emisiones de CO₂.

Los problemas de optimización estructural pueden resolverse mediante métodos exactos, como la programación matemática, o mediante métodos heurísticos que imitan procesos naturales (como la evolución genética o el comportamiento de enjambres). Aunque los métodos heurísticos son más eficientes para problemas complejos y no lineales, como los que involucran grandes estructuras tridimensionales, requieren un alto coste computacional. Para abordar este problema, los autores proponen el uso de metamodelos, que son modelos simplificados que permiten realizar simulaciones con un consumo computacional mucho menor sin sacrificar demasiada precisión. En este estudio, se utiliza un metamodelo basado en Kriging, una técnica que permite aproximar el comportamiento de estructuras complejas.

Además, el estudio introduce una novedad crucial: la inclusión de la interacción suelo-estructura (SSI, por sus siglas en inglés) durante el modelado. Esta interacción, que muchas veces se ignora en los modelos tradicionales, afecta significativamente al comportamiento de la superestructura (el marco de hormigón). Ignorarla puede dar lugar a diseños menos precisos que no tienen en cuenta los asentamientos diferenciales del suelo, lo que puede provocar tensiones adicionales y un mayor deterioro de las estructuras con el tiempo.

Metodología

La investigación emplea un enfoque combinado de optimización heurística convencional y una estrategia basada en Kriging para optimizar marcos espaciales de hormigón armado. El objetivo es reducir las emisiones de CO₂ de las estructuras optimizadas, en línea con los esfuerzos para disminuir el impacto ambiental del sector de la construcción. El estudio incluye tres estudios de caso, cada uno con diferentes configuraciones estructurales (variando la longitud de los vanos y el número de niveles de las estructuras) para generalizar los resultados.

El elemento clave en esta investigación es la inclusión de la interacción suelo-estructura, que afecta al comportamiento global del sistema. Los autores utilizan un modelo de Winkler, que representa el suelo como un conjunto de resortes con rigidez variable en función de las características del suelo, y lo implementan en dos tipos de suelos: uno cohesivo y otro granular. Esta diferenciación es importante porque cada tipo de suelo responde de manera distinta a las cargas, lo que provoca asentamientos que, en última instancia, influyen en las tensiones de la superestructura. La plataforma CSi-SAP2000 se utilizó como motor de cálculo, mientras que el análisis geotécnico y estructural se integró mediante MATLAB.

Resultados

Uno de los hallazgos más destacados del estudio es que la inclusión de la interacción suelo-estructura modifica significativamente los diseños estructurales. En general, las estructuras diseñadas teniendo en cuenta la interacción suelo-estructura requieren más material (mayores cantidades de hormigón y acero), lo que refleja el aumento de tensiones debido a los asentamientos diferenciales. Por ejemplo, en comparación con un modelo con soportes rígidos ideales, las estructuras que consideran la inclusión de la interacción suelo-estructura muestran un aumento del 12,03 % en las emisiones de CO₂ en suelos cohesivos y hasta un 18,81 % en suelos friccionales.

Los elementos estructurales más afectados por la interacción suelo-estructura son las columnas. Esto se debe a que los asentamientos diferenciales incrementan los momentos flectores en las columnas, lo que requiere un refuerzo adicional y secciones más grandes para resistir las nuevas tensiones. En algunos casos, las emisiones de CO₂ asociadas a las columnas aumentaron más del 60 % al considerar la interacción con el suelo. Los resultados son especialmente marcados en suelos granulares, donde los asentamientos diferenciales son más pronunciados.

Además, la metodología basada en metamodelos, asistida por la técnica de Kriging, demostró ser eficaz para lograr optimizaciones con un alto grado de precisión (hasta un 98,24 % en suelos cohesivos y un 98,10 % en suelos granulares), todo ello reduciendo el tiempo de cálculo en aproximadamente un 90 % en comparación con los métodos heurísticos convencionales.

Implicaciones

Este estudio tiene importantes implicaciones prácticas para el diseño de estructuras de hormigón armado. La inclusión de la interacción suelo-estructura permite obtener diseños más robustos y precisos, lo que reduce el riesgo de fallos prematuros y la necesidad de costosos trabajos de mantenimiento a largo plazo. Los modelos que no tienen en cuenta la interacción suelo-estructura pueden dar como resultado estructuras que inicialmente parecen eficientes, pero que con el tiempo se deterioran más rápidamente debido a las tensiones adicionales no previstas. Por tanto, incluir esta interacción desde el inicio del diseño mejora significativamente la durabilidad y la fiabilidad de las estructuras.

Desde el punto de vista ambiental, el uso de metamodelos para optimizar estructuras de hormigón supone un importante avance. Al reducir el material necesario y mejorar la eficiencia estructural, se contribuye a la reducción de las emisiones de CO₂, un objetivo clave en la lucha contra el cambio climático. Además, la metodología propuesta ofrece un enfoque más sostenible al disminuir los recursos computacionales necesarios para realizar simulaciones complejas.

En conclusión, la inclusión de la interacción suelo-estructura y el uso de metamodelos basados en Kriging suponen una contribución innovadora al campo de la ingeniería estructural. Esta investigación no solo proporciona mejores resultados de diseño, sino que también tiene el potencial de reducir el impacto ambiental de las estructuras de hormigón armado, lo que hace que el sector de la construcción sea más sostenible y eficiente.

Referencia:

NEGRÍN, I.; KRIPKA, M.; YEPES, V. (2023). Metamodel-assisted meta-heuristic design optimization of reinforced concrete frame structures considering soil-structure interaction. Engineering Structures, 293:116657. DOI:10.1016/j.engstruct.2023.116657

Este artículo está publicado en abierto, por lo que puedes descargar aquí mismo:

Descargar (PDF, 8.18MB)

Hormigonado con tubería Tremie

El método Tremie, de llenado por flujo inverso, se utiliza para hormigonar elementos estructurales de difícil acceso, como, por ejemplo, pantallas y pilotes, especialmente en presencia del nivel freático o en excavaciones en las que se empleen lodos de perforación. Con este procedimiento, el hormigón se coloca mediante un tubo vertical de acero cuyo extremo superior tiene forma de embudo. El extremo inferior del tubo se mantiene sumergido en el hormigón fresco sin contacto con el agua.

El hormigón se bombea de forma continua a través de una tubería, deslizándose hacia el fondo y desplazando el agua y las impurezas hacia la superficie. El tubo se coloca por tramos de varias longitudes para adaptarse a la profundidad del elemento que se va a hormigonar y está provisto de un embudo en la parte superior y de elementos de sujeción y suspensión.

En el fondo del tubo Tremie hay una válvula para evitar que el hormigón entre en contacto con el agua. El tubo debe llegar hasta el fondo de la perforación antes de iniciar el vertido del hormigón. Al principio, se debe elevar algunos centímetros para poner en marcha el flujo de hormigón y asegurar un buen contacto entre este y el fondo de la perforación. Se debe evitar el contacto con el agua. Antes de retirar el tubo completamente, se debe verter en la superficie suficiente de hormigón como para desplazar toda el agua y el hormigón diluido. El hormigón debe fluir fácilmente hacia su ubicación final y consolidarse por su propio peso, sin segregación o vibración que pueda incorporar agua a su masa, lavando el cemento, con la consecuente formación de bolos de arena y grava débilmente cementados.

Los tubos Tremie por gravedad deben tener un diámetro interior mínimo de 150 mm o 6 veces el tamaño máximo del árido, el que sea mayor, según la norma EN 1536. Por lo general, se emplea un diámetro de 250 mm. En el caso de los sistemas Tremie a presión (líneas de bombeo), el diámetro puede ser inferior a 150 mm. Los tubos deben ser de acero, ya que el aluminio reacciona con el hormigón y se separa del lodo de perforación.

Los tramos de tubería deben conectarse mediante un acoplamiento completamente estanco al agua. La longitud habitual de estos tramos varía entre 1 y 5 m. Se prefieren longitudes más largas porque tienen menos juntas, aunque el orden de colocación de las diferentes longitudes debe considerarse según las condiciones específicas de la obra, como la profundidad de la excavación, la altura de la tolva y el empotramiento en la primera retirada del tubo, así como durante las últimas descargas a baja presión hidrostática.

En general, los tubos deben separarse en cada junta después de cada uso y guardarse en un soporte Tremie para una limpieza adecuada. Se han producido roturas en las uniones durante la manipulación del Tremie, por lo que se recomienda realizar inspecciones visuales completas.

Los tubos sin juntas pueden utilizarse en excavaciones de poca profundidad, siempre que su manipulación lo permita. La tolva debe tener el mayor volumen posible para garantizar un suministro continuo de hormigón al tubo durante su colocación inicial. Los tubos deben ser lisos, limpios y rectos para minimizar la resistencia por fricción al flujo de hormigón.

Los pilotes suelen ser circulares y, por lo general, es suficiente una tubería central dentro de la perforación. Para los muros de pantalla, las normas especifican distintos límites para la distancia de flujo horizontal, que van de 1,8 a 2,5 m, con un máximo de 3 m. Se recomienda limitar la distancia a 2 m. Distancias mayores, de hasta 3 m, podrían ser aceptables si se ha demostrado que la trabajabilidad del hormigón es suficiente, combinada con una separación adecuada de las barras de armadura y un recubrimiento de hormigón superior a los valores mínimos establecidos. Los ensayos a escala real o las simulaciones numéricas, en particular mediante estudios comparativos, pueden ayudar a determinar los valores adecuados.

Los tubos deben colocarse de la manera más simétrica posible para evitar subidas irregulares del nivel del hormigón. En el caso de un solo tubo, este debe colocarse en el centro. Si se utilizan dos tubos, deben situarse aproximadamente a 1/4 de la longitud del panel desde cada extremo.

El inicio del hormigonado es uno de los pasos más críticos de todo el proceso de vertido, ya que el primer hormigón debe separarse del lodo de perforación.

En el método de hormigonado inicial en seco (a menudo confundido con el «vertido en seco»), el extremo del tubo está cerrado y el hormigón solo entra en contacto con el fluido de soporte una vez que sale del tubo. Se coloca una placa de acero o madera contrachapada con un anillo de sellado en la parte inferior del tubo para mantener el fluido de perforación fuera de la tubería durante su descenso al fondo de la excavación. A continuación, se descarga el hormigón directamente en el tubo seco, elevando el tubo entre 0,1 m y 0,2 m para permitir que el hormigón fluya en la excavación. En vertidos profundos, puede ser difícil evitar que el fluido entre en el tubo a través de las juntas o que este flote.

Con el método de colocación inicial en húmedo, se debe utilizar un medio de separación cuando el tubo esté lleno de fluido. Ejemplos de estos «tapones» incluyen gránulos de vermiculita (posiblemente agrupados en un saco), pelotas de goma inflables, esponjas, y bolas o cilindros de espuma. A veces se utiliza una placa de acero en la base de la tolva que se levanta con una grúa cuando la tolva está llena. El tapón debe evitar que la carga inicial de hormigón se mezcle con el fluido de perforación, lo que causaría segregación dentro del Tremie.

Para iniciar el hormigonado, el tubo debe bajarse hasta el fondo de la excavación y luego levantarse una pequeña altura (no mayor que el diámetro del tubo) para iniciar el flujo de hormigón y permitir que el tapón salga por la base del Tremie. El tapón deslizante de vermiculita debe tener una longitud dos veces el diámetro del tubo y que este no debe levantarse más de 0,2 m desde la base. Por razones prácticas, el método de colocación inicial en húmedo es el método preferido.

La Figura 3 muestra las condiciones de presión antes y durante las etapas del vertido, y destaca que, antes del primer corte, el tubo debe estar suficientemente sumergido. No obstante, debido a los aspectos dinámicos del flujo del hormigón, el nivel real de hormigón en el tubo, especialmente después de una interrupción tras el vertido inicial, puede ser más bajo que el punto de equilibrio hidrostático, tal como indica la Figura 3.

El nivel de hormigón necesario debe evaluarse para cada condición específica del lugar. Sin embargo, en la mayoría de los casos se requiere un mínimo de 5 m, o 6 m, según la norma EN 1536, antes del primer corte del Tremie. Es esencial contar con un volumen suficiente de hormigón en la obra, definido como la cantidad necesaria para llenar la altura mínima, antes de comenzar el vertido.

El Tremie requiere un mínimo de empotramiento en el hormigón previamente vertido. Las normas de ejecución europeas (EN 1536 y EN 1538) establecen un empotramiento mínimo que varía entre 1,5 y 3 m, siendo los valores más altos aplicables a excavaciones de mayor tamaño. En general, se acepta en la práctica un empotramiento mínimo de 3 m.

Cuando se utiliza una entubación recuperable durante el vertido de hormigón al Tremie, es importante considerar la extracción de los tramos de entubación al determinar el empotramiento mínimo del Tremie. La extracción de los tramos de entubación recuperable provocará un descenso en el nivel del hormigón, ya que se ocupará el espacio anular dejado por la entubación. Antes de retirar un tramo de entubación, la profundidad de empotramiento del Tremie debe ser suficiente para garantizar que se mantenga el empotramiento mínimo requerido después del descenso del hormigón.

Cuando se utilizan dos o más tubos Tremie, el extremo inferior de los tubos debe mantenerse a un nivel uniforme, salvo que la base esté escalonada y requiera medidas especiales iniciales.

Para asegurar un flujo adecuado del hormigón, el peso del hormigón dentro de la tubería Tremie debe superar:

La resistencia fuera de la base del tubo Tremie (presión hidrostática del fluido).
La resistencia del hormigón ya vertido.
La fricción entre el hormigón y la superficie interna de la tubería Tremie.

Algunos autores se refieren al «punto de equilibrio hidrostático» como el momento en que la fuerza de gravedad dentro del Tremie está equilibrada con la resistencia al flujo (véase la figura 3). Cuando se añade hormigón por encima de este punto de equilibrio, se provoca el flujo del hormigón. A mayor velocidad de vertido, más rápido será el flujo a través de la salida del Tremie.

El hormigón debe fluir libremente por el Tremie sin necesidad de bombeo, es decir, sin requerir elevación y descenso frecuentes del Tremie. Subir y bajar el Tremie para mantener el flujo indica una falta de trabajabilidad. Esto puede afectar a la configuración del flujo de hormigón y conlleva el riesgo de mezcla con el fluido de perforación y con material contaminado en la parte superior del hormigón, lo que puede dar lugar a la acumulación de detritos.

Os dejo algunos vídeos sobre este método de vertido del hormigón. Espero que os gusten.

Colocación de una tubería Tremie:

Hormigonado de un muro pantalla con tubería Tremie:

Lubricación de una tubería Tremie con lechada de cemento:

Descargar (PDF, 3.34MB)

Referencias:

ACI COMMITTEE 304. Guide for Measuring, Mixing, Transporting, and Placing Concrete. ACI 304R-00.

BUSTILLO, M. (2008). Hormigones y morteros. Fueyo Editores, Madrid, 721 pp.

CALAVERA, J. et al. (2004). Ejecución y control de estructuras de hormigón. Intemac, Madrid, 937 pp.

FERNÁNDEZ CÁNOVAS, M. (2004). Hormigón. 7ª edición, Colegio de Ingenieros de Caminos, Canales y Puertos. Servicio de Publicaciones, Madrid, 663 pp.

GALABRU, P. (1964). Tratado de procedimientos generales de construcción. Obras de fábrica y metálicas. Editorial Reverté, Barcelona, 610 pp.

MARTÍ, J.V.; YEPES, V.; GONZÁLEZ, F. (2014). Fabricación, transporte y colocación del hormigón. Apuntes de la Universitat Politècnica de València, 189 pp.

TIKTIN, J. (1994). Procesamiento de áridos: instalaciones y puesta en obra de hormigón. Universidad Politécnica de Madrid. Escuela Técnica Superior de Ingenieros de Caminos, Canales y Puertos. Madrid, 360 pp. ISBN: 84-7493-205-X.

YEPES, V. (2020). Procedimientos de construcción de cimentaciones y estructuras de contención. Colección Manual de Referencia, 2ª edición. Editorial Universitat Politècnica de València, 480 pp. Ref. 328. ISBN: 978-84-9048-903-1.

YEPES, V. (2023). Maquinaria y procedimientos de construcción. Problemas resueltos. Colección Académica. Editorial Universitat Politècnica de València, 562 pp. Ref. 376. ISBN 978-84-1396-174-3

Cursos:

Curso de fabricación y puesta en obra del hormigón.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Tipo de cemento para hormigones resistentes a sulfatos en cimentaciones

Figura 1. Ataque por sulfatos del hormigón. https://anfapa.com/articulos-tecnicos-morteros-de-reparacion-de-hormigon/1164/causas-quimicas-del-deterioro-del-hormigon

Los sulfatos son compuestos químicos que se encuentran en una gran variedad de concentraciones en el suelo, las aguas subterráneas, las aguas superficiales y las aguas marinas. Entre los sulfatos de origen natural se encuentran algunos suelos orgánicos, suelos con turbas y algunos suelos arcillosos. Otra fuente natural de sulfatos son los sulfatos de origen biológico, industrial o minero presentes en el agua de mar.

La mayoría de los suelos contienen sulfatos, que pueden presentarse en formas tales como calcio, magnesio, sodio, amonio y potasio, ya sea en el suelo mismo o en las aguas subterráneas. Es habitual que las cimentaciones de las estructuras se sitúen en este tipo de suelos, por lo que existe la posibilidad de que los sulfatos presentes ataquen el hormigón. El deterioro del hormigón debido al ataque de sulfatos se distingue por una reacción química en la que el ion sulfato, actuando como agente corrosivo, interactúa con componentes como aluminato, iones de sulfato, calcio y grupos oxhidrilo del cemento Portland endurecido, así como de otros cementos que contienen clínker de Portland, generando principalmente etringita y, en menor medida, yeso, así como una descalcificación. Este fenómeno se denomina «formación diferida de etringita» o «etrignita secundaria». Estas reacciones expansivas también pueden ocasionar fisuras, desprendimientos y pérdida de resistencia en el hormigón, dado que ocurren después de que el hormigón ha alcanzado su estado endurecido y se ha vuelto un cuerpo rígido.

El ataque de los sulfatos derivados de las sales es un fenómeno reconocido desde hace décadas. Ya en 1887, Candlot observó cómo los morteros utilizados en la construcción de las fortificaciones de París se deterioraban, particularmente en las zonas en las que estuvieron en contacto con agua que contenía sulfatos (selenitosas). Esta reacción química genera expansión en la pasta y crea una presión capaz de romperla y, finalmente, desintegrar el hormigón. Es sabido que el sulfato cálcico se combina con la alúmina del cemento para formar la sal de Candlot (etringita), un sulfo-aluminato cálcico que provoca un notable aumento de volumen.

La naturaleza y el alcance de los daños en el hormigón variarán en función de la concentración de sulfatos, el tipo de cationes presentes en la solución de sulfato (ya sea sodio o magnesio), el pH de la solución y, por supuesto, la microestructura de la pasta de cemento endurecida. Algunos tipos de cemento son más susceptibles al sulfato de magnesio que al sulfato de sodio. El mecanismo principal consiste en la sustitución del calcio en el silicato de calcio hidratado, que forma parte de la matriz de cemento, lo que provoca la pérdida de las propiedades de unión de la matriz.

Por lo general, los sulfatos en estado sólido no generan un daño significativo al hormigón; sin embargo, cuando se encuentran en estado líquido, pueden penetrar los vacíos de la estructura y reaccionar con los productos de cemento hidratado. Entre los sulfatos, el de calcio tiende a causar menores daños debido a su baja solubilidad, mientras que el sulfato de magnesio representa un riesgo mayor.

La mayoría de estos sulfatos interactúan con el hidróxido de calcio y los aluminatos de calcio hidratados presentes en el hormigón, lo que provoca cambios en el volumen de la pasta de cemento y, en consecuencia, el deterioro de la estructura de hormigón. Además, el sulfato de magnesio, junto con el hidróxido de calcio, puede reaccionar con el silicato de calcio hidratado, lo que provoca la pulverización del hormigón en masa. En un hormigón poroso, estos ataques encuentran una vía fácil para su acción destructora.

Figura 2. Corrosión en ambiente marino. https://e-struc.com/2017/05/09/patologias-asociadas-la-prescripcion-del-hormigon/

Por otra parte, el hormigón también se ve afectado por los cloruros, que provocan principalmente la corrosión de las armaduras. Los iones cloruro, ya procedan del agua marina o de las sales utilizadas en el deshielo, tienen la capacidad de penetrar a través de los poros del hormigón, tanto cuando estos están completamente saturados como parcialmente. Esta penetración puede desencadenar diversos fenómenos. En la superficie del hormigón, los efectos del ataque por cloruros se manifiestan mediante una fisuración irregular, que resulta de la exposición de las armaduras y su consiguiente corrosión generalizada. Esto conduce a la desintegración gradual del hormigón. Es muy importante recordar que el ambiente marino se considera agresivo hasta una distancia de 5 km de la costa.

Los cementos resistentes a los sulfatos (SR) o al agua de mar (MR) son muy útiles para obras en contacto con terrenos yesíferos o aguas selenitosas y deben tener un bajo contenido en aluminatos. Este tipo de cementos tienen limitado en su composición un contenido de aluminato tricálcico y de alumino-ferrito tetracálcico, según la norma UNE-EN 197-1. Esta limitación en el aluminato tricálcico implica un bajo calor de hidratación, una menor retracción y un desarrollo más lento de las resistencias. A cambio, disminuye la trabajabilidad de las mezclas.

Según la vigente Instrucción de Recepción de Cementos (a fecha de hoy, la RC-16), se consideran cementos resistentes a los sulfatos, además de los definidos en el Anejo I relativo a la norma UNE-EN 197-1 (SR), aquellos con la característica adicional de resistencia a los sulfatos definidos en la norma UNE 80303-1 (SRC). Asimismo, se consideran cementos resistentes al agua de mar aquellos con la característica adicional de resistencia al agua de mar, definidos en la norma UNE 80303-2.

Se usarán cementos resistentes a los sulfatos en obras de hormigón en masa o armado, siempre que su contenido, expresado en iones sulfato, cuyos contenidos sean igual o mayor que 600 mg/l en el caso de aguas, o 3.000 mg/kg en el caso de suelos. Según el Capítulo 7 del Código Estructural, estos límites se ven superados en el caso de las clases de exposición XA2 y XA3, correspondientes al ataque medio y fuerte en un medio agresivo (no sería, por tanto, necesario un cemento sulforresistente en la clase XA1). En el caso de que un elemento estructural de hormigón en masa, armado o pretensado se encuentre sometido al ataque de agua de mar, el cemento a emplear deberá tener la característica adicional de resistencia al agua de mar o, en su defecto, la característica adicional de resistencia a los sulfatos. Lo anterior no será de aplicación si se trata de agua de mar o el contenido en cloruros es superior a 5000 mg/l (art. 43.3.4.1 del Código Estructural).

En el caso de elementos de hormigón en masa en contacto con agua de mar y, por tanto, sometidos a una clase de exposición XA2, y en el caso de elementos de hormigón armado o pretensado que vayan a estar sometidos a una clase de exposición XS2 o XS3, se utilizará un cemento con la característica adicional MR, SR o SRC, según la Instrucción para la recepción de cementos vigente (Art. 43.3.4.2 del Código Estructural).

El Código Estructural recoge en su Anejo 6 las recomendaciones para la selección del tipo de cemento que se debe emplear en hormigones estructurales. Este anejo no hace más que aconsejar, con carácter general, las condiciones que debe cumplir el cemento para su empleo según la instrucción vigente para la recepción de cementos. Además, el tipo de cemento deberá elegirse considerando la aplicación del hormigón, las circunstancias del hormigonado y las condiciones de agresividad ambiental a las que va a estar sometido el elemento de hormigón.

La aplicación estructural, en el caso de las cimentaciones, diferencia entre las ejecutadas con hormigón en masa y las realizadas con hormigón armado. En ambos casos, es necesario cumplir las prescripciones de la vigente Instrucción de Recepción de Cementos relativas al empleo de la característica adicional de resistencia a los sulfatos (SR o SRC) o al agua de mar (MR), cuando corresponda.

En el caso de cimentaciones de hormigón en masa, son muy adecuados los cementos comunes tipo CEM IV/B, siendo adecuados el resto de cementos comunes, excepto los CEM II/A-Q, CEM II/B-Q, CEM II/A-W, CEM II/B-W, CEM II/A-T, CEM II/B-T y CEM III/C. En todos los casos, se recomienda la característica adicional de bajo calor de hidratación (LH).
Si se trata de cimentaciones de hormigón armado, son muy adecuados los cementos comunes tipo CEM I y CEM II/A, siendo adecuados el resto de cementos comunes a excepción de los CEM III/B, CEM III/C, CEM IV/B, CEM II/A-Q, CEM II/B-Q, CEM II/A-W, CEM II/B-W, CEM II/A-T y CEM II/B-T.

Figura 3. Cemento sulforresistente CEM I 42,5 R-SR5

Atendiendo a la clase de exposición, los tipos de cementos recomendados para la clase XA (ataque químico al hormigón por sulfatos) son los mismos que los aconsejados para la clase XS (corrosión de las armaduras por cloruros de origen marino). En ambos casos, son muy adecuados los cementos CEM II/S, CEM II/V (preferentemente los CEM II/B-V), CEM II/P (preferentemente los CEM II/B-P), CEM II/A-D, CEM III, CEM IV (preferentemente los CEM IV/A) y CEM V/A. Se recuerda que en la clase de exposición XS, es necesario emplear cementos que cumplan las prescripciones relativas a la característica adicional de resistencia al agua de mar (MR).

Para el caso de las clases XA2 o XA3 (moderada o alta agresividad química), es necesario emplear cementos que cumplan las prescripciones relativas a la característica adicional de resistencia a los sulfatos (SR o SRC), tal y como establece el articulado del Código. En los casos en que el elemento esté en contacto con agua de mar, será únicamente necesario que cumplan las prescripciones relativas a la característica adicional de resistencia al agua de mar (MR).

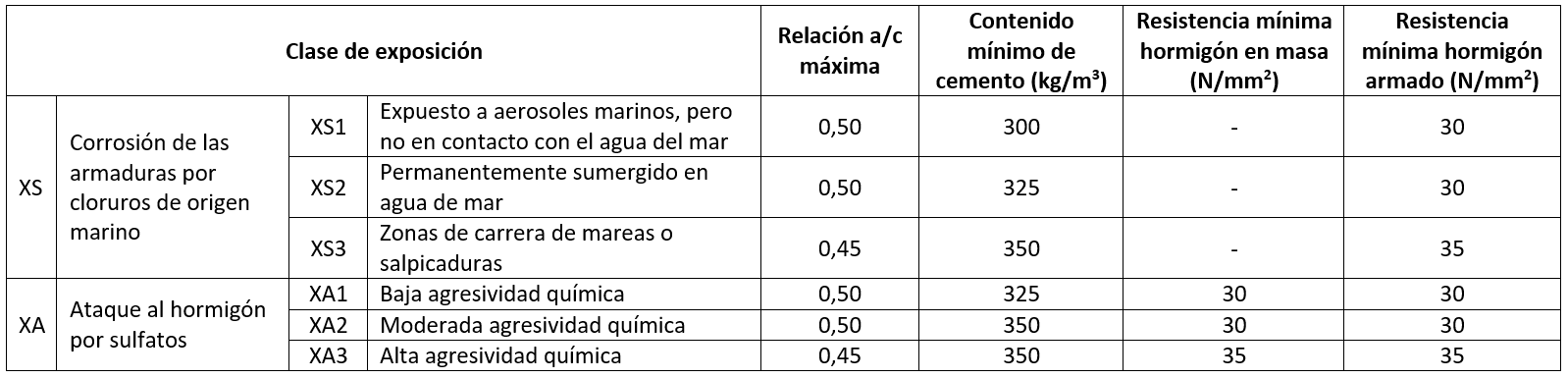
Una relación agua/cemento baja en la dosificación de un hormigón se ve menos afectada por los sulfatos que si es alta, pues provoca que el hormigón sea menos permeable. Además, un contenido de cemento elevado garantiza una mayor durabilidad del hormigón. Es por ello que la Tabla 43.2.1.a del Código indica una relación agua/cemento máxima de 0,50 para las clases XS1 (expuesto a aerosoles marinos, pero no en contacto con el agua del mar) y XS2 (permanentemente sumergido en agua de mar), que se reduce a 0,45 en XS3 (zonas de carrera de mareas o sapicaduras). El contenido mínimo de cemento (kg/m³) será de 300, 325 y 350 para XS1, XS2 y XS3, respectivamente. En el caso de ambiente XA1 (débil agresividad química) y XA2 (moderada agresividad química), la máxima relación agua/cemento es de 0,50, mientras que en XA3 (alta agresividad química), es de 0,45. El contenido mínimo de cemento (kg/m³) será de 325, 350 y 350 para XA1, XA2 y XA3, respectivamente.

La Tabla 43.2.1.b del Código indica la resistencia característica mínima alcanzable para un hormigón fabricado con un cemento de categoría resistente 32,5 R con los contenidos mínimos de cemento y la máxima relación agua/cemento indicados en la Tabla 43.2.1.a del Código. Para hormigón en masa, la exposición XS no tiene mínimos, mientras que, para hormigón armado, es de 30 N/mm² para XS1 y XS2, y de 35 N/mm² para XS3. En las exposiciones XA1 y XA2, la resistencia mínima es de 30 N/mm² tanto en hormigón armado como en hormigón en masa, mientras que para XA3 es de 35 N/mm², en cualquier caso.

Además, una adecuada colocación del hormigón, con un control del vibrado y del curado, puede mejorar su resistencia a los sulfatos, siempre y cuando se cumplan las condiciones anteriormente mencionadas. Tampoco debe olvidarse que, en el caso del hormigón armado, deben guardarse unos recubrimientos mínimos que dependerán del tipo de cemento utilizado, de la vida útil de proyecto y de la clase de exposición, según se desprende del Capítulo 9 del Código Estructural, relativo a la durabilidad de las estructuras de hormigón.

Tabla. Requisitos de dosificación y de resistencia mínima esperada del hormigón para clases de exposición XS y XA, según el Código Estructural.

Os dejo unos vídeos explicativos.

También os dejo un artículo, que creo de interés.

Descargar (PDF, 4.68MB)

Referencias:

ACI COMMITTEE 304. Guide for Measuring, Mixing, Transporting, and Placing Concrete. ACI 304R-00.

CALAVERA, J. et al. (2004). Ejecución y control de estructuras de hormigón. Intemac, Madrid, 937 pp.

GALABRU, P. (1964). Tratado de procedimientos generales de construcción. Obras de fábrica y metálicas. Editorial Reverté, Barcelona, 610 pp.

MARTÍ, J.V.; YEPES, V.; GONZÁLEZ, F. (2014). Fabricación, transporte y colocación del hormigón. Apuntes de la Universitat Politècnica de València, 189 pp.

Cursos:

Curso de fabricación y puesta en obra del hormigón.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Interacción suelo-estructura en el diseño óptimo de pórticos de edificación

Hemos presentado en la 7th International Conference on Mechanical Models in Structural Engineering una comunicación sobre la implementación de un modelo que considere la interacción entre el suelo y la estructura (SSI) en el diseño óptimo de pórticos de hormigón armado en edificación. El trabajo propone una metodología para simular la interacción suelo-estructura en los procesos de optimización estructural, utilizando un modelo tipo Winkler que considera la deformación adicional de la superestructura durante la carga, lo que conduce a diseños sostenibles más eficientes y duraderos. El objetivo es crear un escenario más realista considerando el asentamiento del suelo y su influencia en el coeficiente de rigidez, que no se tiene en cuenta en los métodos tradicionales de soportes rígidos o articulados, lo que lleva a un diseño de superestructura ineficiente. El estudio se enmarca dentro del proyecto de investigación HYDELIFE que dirijo como investigador principal en la Universitat Politècnica de València.

El estudio compara los diseños optimizados de las estructuras con los soportes clásicos (métodos tradicionales) y el modelo sugerido, lo que demuestra la influencia de considerar la interacción entre el suelo y la estructura en la eficiencia del diseño de la superestructura. Los resultados muestran que el uso de soportes tradicionales conduce a diseños ineficientes, lo que pone de relieve la necesidad de modelos más realistas que tengan en cuenta esta interacción.

El documento también analiza el comportamiento de los diferentes tipos de suelo y cómo se refleja en el modelo propuesto. Considera tanto los suelos cohesivos como los granulares, destacando los asentamientos diferenciales y las tensiones adicionales que se producen en los modelos con interacción, y que no ocurren en los modelos con soportes rígidos.

Los resultados de este estudio se pueden resumir de la siguiente forma:

Los diseños optimizados de los modelos con interacción generan más emisiones que los modelos tradicionales, lo que indica que la superestructura de los modelos que consideran el SSI está más estresada. Sin embargo, esto no significa que no tener en cuenta la interacción sea más beneficioso.
Las estructuras con soportes rígidos requieren menos material en la superestructura, pues están menos estresadas, pero no reflejan los asentamientos diferenciales que existen en la práctica.
Los suelos granulares son más propensos a los asientos diferenciales, y el aumento de la curvatura resultante de los asientos diferenciales afecta más a las columnas que a las vigas.
Las diferencias más significativas entre los modelos con SSI y los modelos con soportes clásicos se observan en el estudio de caso en el que la carga axial que llega a los cimientos es mayor debido a un nivel adicional, lo que agudiza el fenómeno del asiento diferencial.
Los resultados demuestran la influencia del SSI en la eficiencia del diseño de la superestructura, y destacan la necesidad de modelos más realistas que tengan en cuenta el SSI para diseños sostenibles más eficientes y duraderos.

Abstract:

This paper proposes a methodology to simulate the soil-structure interaction (SSI) in structural optimization processes. The aim is to create a scenario more aligned with reality, which is not reflected in the traditional methods of considering perfectly rigid or articulated supports. A Winkler-type model is proposed where a hyperbolic equation that relates the pressure p with the settlement S is used to calculate the stiffness coefficient k. This coefficient simulates the interaction that causes additional deformation of the superstructure during the loading process, increasing internal forces. Several reinforced concrete frame structures with traditional rigid supports and the proposed SSI model are optimized to demonstrate the influence of this phenomenon. The results show that using traditional supports, as is commonly done, leads to inefficient superstructure design. Therefore, the proposed methodology is conducive to creating more realistic models that allow for more efficient and durable sustainable designs.

Keywords:

Soil-structure interaction; reinforced concrete; frame structure; optimization; Winkler model.

Reference:

NEGRÍN, I.; KRIPKA, M.; YEPES, V. (2023). Model for considering soil-structure interaction and its implementation in the optimal design of RC frame structures. 7th International Conference on Mechanical Models in Structural Engineering, CMMoST 2023. 29 nov – 01 dec, Málaga (Spain).

Descargar (PDF, 523KB)

Cálculo de la producción de un compactador

Figura 1. Compactador monocilíndrico vibratorio autopropulsado Cat CS10 GC. https://www.interempresas.net/ObrasPublicas/Articulos/346172-Caterpillar-presenta-sus-nuevos-compactadores-vibratorios-de-suelos-de-un-solo-tambor.html

La producción de un compactador es directamente proporcional a su velocidad de trabajo, al ancho eficaz del compactador y al espesor de la tongada una vez compactada, e inversamente proporcional al número de pasadas necesarias. El ancho eficaz sería la diferencia entre la anchura del órgano de trabajo del compactador y el solape necesario para garantizar la compactación entre los distintos carriles.

Debido a la multitud de factores que influyen en la compactación, para grandes volúmenes de obra, se aconseja la realización de tramos de prueba, donde se pueden establecer los criterios que, bajo la perspectiva económica, sean óptimos para llegar a la compactación especificada. Los tramos de prueba no suelen estar justificados en el caso de que los materiales sean suficientemente homogéneos y siempre resulta interesante cuando nos encontramos ante yacimientos importantes. En otro caso, no resulta económica su ejecución. Estos tramos de prueba están formados por una cuña, cuyo espesor llega hasta el máximo que se considere para el equipo empleado.

Este tipo de cuestiones se tratan ampliamente en el curso sobre “Compactación superficial y profunda de suelos en obras de ingeniería civil y edificación”. Toda la información la puedes encontrar en esta página: https://ingeoexpert.com/cursos/curso-de-compactacion-superficial-y-profunda-de-suelos-en-obras-de-ingenieria-civil-y-edificacion/. Además, este os recomiendo también el curso sobre “Gestión de costes y producción de la maquinaria empleada en la construcción”, cuya información podéis ver aquí: https://ingeoexpert.com/cursos/curso-de-gestion-de-costes-y-produccion-de-la-maquinaria-empleada-en-la-construccion/

A continuación os dejo un par de nomogramas que permiten el cálculo directo de esta producción. En uno de ellos se han utilizado tanto las unidades del sistema internacional como las anglosajonas. Estos nomogramas se han elaborado en colaboración con el profesor Pedro Martínez Pagán, de la Universidad Politécnica de Cartagena.

Referencias:

MORILLA, I. (2012). Interpretación de los ensayos geotécnicos en suelos. 627 pp., Madrid.

YEPES, V. (1997). Equipos de movimiento de tierras y compactación. Problemas resueltos. Colección Libro Docente n.º 97.439. Ed. Universitat Politècnica de València. 253 pág. ISBN: 84-7721-551-0.

YEPES, V. (2021). Procedimientos de construcción para la compactación y mejora del terreno. Colección Manual de Referencia, 1ª edición. Editorial Universitat Politècnica de València, 426 pp. Ref. 428. ISBN: 978-84-9048-603-0.

YEPES, V. (2022). Gestión de costes y producción de maquinaria de construcción. Colección Manual de Referencia, serie Ingeniería Civil. Editorial Universitat Politècnica de València, 243 pp. Ref. 442. ISBN: 978-84-1396-046-3

Cursos:

Curso de compactación superficial y profunda de suelos en obras de ingeniería civil y edificación.

Curso de gestión de costes y producción de la maquinaria empleada en la construcción.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Maquinaria y procedimientos de construcción: Problemas resueltos

Os presento el libro que he publicado sobre maquinaria y procedimientos de construcción. Se trata de una completa colección de 300 problemas resueltos, abarcando aspectos relacionados con la maquinaria, medios auxiliares y procedimientos de construcción. Su contenido se enfoca en la mecanización de las obras, costos, disponibilidad, fiabilidad y mantenimiento de equipos, estudio del trabajo, producción de maquinaria, sondeos y perforaciones, técnicas de mejora del terreno, control y abatimiento del nivel freático, movimiento de tierras, equipos de dragado, explosivos y voladuras, excavación de túneles, instalaciones de tratamiento de áridos, compactación de suelos, ejecución de firmes, maquinaria auxiliar como bombas, compresores o ventiladores, cables y equipos de elevación, cimentaciones y vaciados, encofrados y cimbras, fabricación y puesta en obra del hormigón, organización y planificación de obras.

Es un libro, por tanto, muy enfocado a los ámbitos de la ingeniería de la construcción, tanto en el ámbito de la edificación, de la minería o de la ingeniería civil. Además, se incluyen 27 nomogramas originales y 19 apéndices para apoyar tanto a estudiantes de ingeniería o arquitectura, como a profesionales que enfrentan desafíos similares en su práctica diaria en obra o proyecto. La colección se complementa con un listado de referencias bibliográficas que respaldan los aspectos teóricos y prácticos abordados en los problemas. Estos problemas son similares a los tratados durante las clases de resolución de casos prácticos en la asignatura de Procedimientos de Construcción del Grado en Ingeniería Civil de la Universitat Politècnica de València (España). Por tanto, el libro resulta adecuado tanto para estudiantes de grado como para cursos de máster relacionados con la ingeniería civil y la edificación.

El libro tiene 562 páginas. Este libro lo podéis conseguir en la propia Universitat Politècnica de València o bien directamente por internet en esta dirección: https://www.lalibreria.upv.es/portalEd/UpvGEStore/products/p_376-7-1

Sobre el autor: Víctor Yepes Piqueras. Doctor Ingeniero de Caminos, Canales y Puertos. Catedrático de Universidad del Departamento de Ingeniería de la Construcción y Proyectos de Ingeniería Civil de la Universitat Politècnica de València. Número 1 de su promoción, ha desarrollado su vida profesional en empresas constructoras, en el sector público y en el ámbito universitario. Ha sido director académico del Máster Universitario en Ingeniería del Hormigón (acreditado con el sello EUR-ACE®), investigador del Instituto de Ciencia y Tecnología del Hormigón (ICITECH) y profesor visitante en la Pontificia Universidad Católica de Chile. Imparte docencia en asignaturas de grado y posgrado relacionadas con procedimientos de construcción y gestión de obras, calidad e innovación, modelos predictivos y optimización en la ingeniería. Sus líneas de investigación actuales se centran en la optimización multiobjetivo, la sostenibilidad y el análisis de ciclo de vida de puentes y estructuras de hormigón.

Referencia:

A continuación os paso las primeras páginas del libro, con el índice, para hacerse una idea del contenido desarrollado.

Descargar (PDF, 17.88MB)

Un estudio de la UPV permite abaratar costes y reducir el impacto medioambiental en la construcción de túneles subterráneos

Figura 1. Marcos prefabricados en Vilaseca. Cortesía de ANDECE.

Un estudio realizado por investigadores de la Universitat Politècnica de València (UPV), pertenecientes al Instituto de Ciencia y Tecnología del Hormigón (ICITECH), ofrece una alternativa más económica y sostenible para la construcción con marcos prefabricados de hormigón de infraestructuras de transporte, como túneles subterráneos, edificios y otras estructuras. Sus resultados han sido publicados en la revista Materials.

En su trabajo, enmarcado dentro del proyecto Hydelife, han desarrollado diferentes algoritmos cuya aplicación permite ahorros económicos de hasta un 24% en el coste final de la estructura, disminuyendo los costes asociados con la producción y el transporte de materiales.

Además, según las estimaciones que ha realizado el equipo del ICITECH-UPV, permitiría optimizar el uso de materiales en la estructura y reducir alrededor de un 30% de las emisiones de CO₂ asociadas a la construcción.

“Pensemos una obra lineal donde tengamos, por ejemplo, 1000 metros de un túnel subterráneo que se pueda ejecutar con marcos prefabricados. Además del ahorro económico, en nuestro trabajo, estimamos que la reducción de 1 euro en el coste final de un marco de hormigón armado es equivalente a evitar la emisión de cerca de 2 kg de CO₂”, destaca Víctor Yepes, investigador del Instituto ICITECH de la Universitat Politècnica de València.

Así, este estudio presenta una alternativa sostenible y eficiente en términos de recursos para los marcos tradicionales de hormigón armado in situ.

“Nuestro objetivo era ampliar el conocimiento sobre la tipología estructural de marcos prefabricados articulados de hormigón y su empleo como sustituto de los marcos tradicionales de hormigón armado colado in situ. Y los resultados que hemos obtenido constatan su enorme potencial para grandes infraestructuras. El estudio es de especial interés para ámbitos como la ingeniería civil y arquitectura y, sobre todo, para las empresas de prefabricados de hormigón”, concluye Víctor Yepes.

Referencia:

RUIZ-VÉLEZ, A.; ALCALÁ, J.; YEPES, V. (2023). Optimal design of sustainable reinforced concrete precast hinged frames. Materials, 16(1):204. DOI:10.3390/ma16010204.

Os paso a continuación la repercusión de esta noticia en algunos medios de prensa.

Marcos prefabricados de hormigón para la construcción, una opción más barata y sostenible

Algoritmos para abaratar costes y reducir el impacto medioambiental al usar marcos prefabricados de hormigón en la construcción

https://24noticias.org/marcos-prefabricados-de-hormigon-alternativa-para-la-construccion/

https://www.levante-emv.com/sostenibilitat/2023/05/25/estudi-upv-revela-com-reduir-87816604.html

Algorithms for cleaner and cheaper construction of underground tunnels

https://www.upv.es/noticias-upv/noticia-14122-mas-sostenible-es.html

https://aplicat.upv.es/exploraupv/ficha-prensa/noticia/14122

https://www.cope.es/actualidad/sociedad/noticias/marcos-prefabricados-hormigon-para-construccion-una-opcion-mas-barata-sostenible-20230521_2719911

https://valenciaplaza.com/marcos-prefabricados-hormigon-construccion-opcion-mas-barata-sostenible

https://noticiasdelaciencia.com/art/46721/algoritmos-para-una-construccion-mas-limpia-y-mas-barata-de-tuneles-subterraneos

Estribos de puente de tierra estabilizada mecánicamente

Figura 1. Estribo de tierra estabilizada mecánicamente. Fuente: http://www.tierra-armada.com/

En situaciones en las que no es factible verter tierra frente al alzado del estribo debido a un terreno con baja capacidad portante, deformable o no se pueden realizar excavaciones, se requiere utilizar técnicas de tierra estabilizada mecánicamente, conocido también como suelo reforzado o bajo el nombre comercial de Tierra Armada®. Estas técnicas también son aplicables en zonas urbanas, donde es necesario evitar el derrame del terraplén y aprovechar las características estéticas que ofrecen este tipo de muros. Consisten en reforzar el material del terraplén mediante pletinas o flejes presentes en las escamas, fabricadas generalmente con materiales galvanizados o de fibra de carbono, que se colocan en el frente del estribo. Estas pletinas absorben eficientemente los empujes horizontales al interactuar con el suelo a través de la fricción.

El muro se complementa con escamas prefabricadas de hormigón, a las cuales se fijan los refuerzos (Figura 1). Estas escamas se entrelazan entre sí, presentando diversas formas, colores y texturas. En el trasdós de estas escamas se alojan armaduras o flejes que contrarrestan el empuje de las tierras mediante el rozamiento. La longitud de las armaduras debe ser igual o mayor a 0,7 veces la altura H del muro. En el caso de estructuras hiperestáticas, que pueden ser muy sensibles a los movimientos del macizo de tierra reforzada, es común separar el apoyo extremo del tablero del muro de tierra reforzada mediante la disposición de lo que podría considerarse como una pila adicional. En la coronación del muro, es posible disponer de un cargadero o durmiente que brinda soporte al tablero. Es frecuente separar el apoyo del tablero del muro mediante la colocación de una pila-estribo ubicada delante de este (Figura 2). La ejecución debe realizarse con cuidado para prevenir patologías, como descensos significativos o abultamiento de la pared exterior, entre otros problemas.

Figura 2. Estribo de tierra estabilizada mecánicamente. Fuente: http://www.tierra-armada.com/

La construcción de este tipo de estribos se caracteriza por ser rápida, sencilla y económica, lo que resulta en ahorros significativos, del orden del 15% al 40%, en comparación con estribos de puente ejecutados mediante sistemas convencionales. No obstante, es fundamental que estos estribos se ejecuten con gran precisión para evitar problemas posteriores como la ruptura de las escamas o desplazamientos.

El cargadero o estribo flotante debe diseñarse de manera que la presión transmitida al macizo de tierra reforzada sea adecuada, evitando una carga excesiva que requiera un alto número de armaduras en los niveles inferiores de escamas. Como referencia, se recomienda dimensionar la planta del durmiente de tal manera que la presión transmitida al lecho no supere los 0,2 MPa.

En el caso de estribos de altura moderada, la distancia mínima requerida entre el borde del durmiente y el paramento es de 10 cm. Por el contrario, para muros de 10 m de altura, dicha distancia no debe ser inferior a 15 cm. Es importante garantizar que el espacio entre el eje de los apoyos del tablero y el borde exterior del paramento no sea inferior a 1 m.

Al considerar las características geométricas de un estribo de tierra estabilizada mecánicamente, es fundamental tener en cuenta varios aspectos clave. Primero, la anchura B del macizo de suelo reforzado, determinada por la longitud de los flejes, debe ser mayor al 70% de H siempre que H sea inferior a 20 m, y mayor al 60 % de H más 2 m en el caso de muros más bajos. Además, la profundidad D del muro en el terreno debe ser de al menos 0,40 m, a menos que esté cimentado sobre un terreno compacto no susceptible a heladas, y generalmente supera el 10 % de H en estribos normales. Asimismo, la presión transmitida por el durmiente debido a las cargas permanentes debe ser inferior a 0,2 MPa, y la distancia entre el eje de los apoyos del tablero y el borde exterior del paramento debe ser de al menos 1 m. Es relevante que el estribo flotante se asiente sobre una capa de suelo tratado con un 3% a 5% de cemento, con un espesor mínimo de 0,50 m. La parte frontal del durmiente debe separarse al menos 10 cm del paramento, y en el caso de estribos con una altura superior a 10 m, se requiere una distancia mínima de 15 cm. Además, el durmiente debe contar con un resguardo mínimo de suelo tratado en su parte trasera de 30 cm.

En algunas ocasiones, se separa la función de contener las tierras de la de soportar el dintel. En este caso, el dintel estará pilotado y se ubicará por delante del muro. Sin embargo, es importante considerar que la carga del muro puede generar rozamientos negativos en los pilotes, lo que podría hacer que trabajen en tracción. Para evitar esta situación, se recomienda construir primero el muro y posteriormente ejecutar el pilotaje del durmiente. Es preferible pilotar lo más tarde posible para permitir que se produzca la mayor parte del asiento del muro antes de su ejecución.

Os dejo algunos vídeos de interés:

También os paso el manual de la Dirección General de Carreteras para el proyecto y ejecución de estructuras de suelo reforzado.

Descargar (PDF, 93.29MB)

Referencias:

DIRECCIÓN GENERAL DE CARRETERAS (1994). Manual para el proyecto y ejecución de estructuras de suelo reforzado. Ministerio de Obras Públicas, Transportes y Medio Ambiente.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Deflexión de una capa compactada

A continuación os dejo una sencilla demostración del asiento que tiene una capa que se ha compactado en función de su espesor inicial y de los pesos específicos anterior y posterior a la compactación. Se trata de una forma indirecta de controlar si se ha alcanzado el grado de compactación deseado. También permite tener una idea de cuánto va a descender la capa una vez compactada.

Si quieres conocer más sobre los aspectos de la compactación, te recomiendo que revises las referencias que dejo al final del post y también este curso en línea sobre “Compactación superficial y profunda de suelos en obras de ingeniería civil y edificación”. Toda la información la puedes encontrar en esta página: https://ingeoexpert.com/cursos/curso-de-compactacion-superficial-y-profunda-de-suelos-en-obras-de-ingenieria-civil-y-edificacion/

Para aquellos nostálgicos de los nomogramas, os dejo uno preparado específicamente para este caso. Espero que os guste.

Descargar (PDF, 121KB)

Referencias:

Cursos:

Curso de compactación superficial y profunda de suelos en obras de ingeniería civil y edificación.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.