movimiento de tierras archivos - El blog de Víctor Yepes

Mejores prácticas para el control del nivel freático en proyectos de construcción.

Figura 1. Control del nivel freático. https://www.flickr.com/photos/wsdot/4997287082/

En este artículo se analiza un documento anexo al final: una guía formal de drenaje que detalla las lecciones aprendidas durante un proyecto de ingeniería civil excepcionalmente complejo en Christchurch (Nueva Zelanda), que se llevó a cabo de 2011 a 2016 tras un terremoto. Proporciona un marco para evaluar, diseñar e implementar el drenaje en programas de reconstrucción de infraestructuras o de recuperación tras desastres naturales, con énfasis en las prácticas de construcción y la geología local.

La guía examina diversos sistemas de control del nivel freático, como sumideros, sistemas de well-points y pozos, y ofrece criterios para seleccionar los métodos según la permeabilidad del suelo y la profundidad de la excavación. Además, establece un sistema para determinar la categoría de riesgo de un proyecto de drenaje y describe las medidas necesarias para mitigar los efectos ambientales y prevenir la subsidencia del terreno.

1.0 Introducción y principios fundamentales.

1.1 La importancia crítica del control del agua subterránea.

El control del nivel freático es un factor determinante para el éxito de cualquier proyecto de construcción que implique excavaciones. Una gestión inadecuada o la ausencia de un control efectivo puede comprometer gravemente la estabilidad de las excavaciones, la integridad de las estructuras permanentes y, en última instancia, la viabilidad económica y temporal del proyecto. El agua subterránea no controlada puede generar riesgos geotécnicos significativos, como la tubificación (piping), que es la erosión interna del suelo por el flujo de agua; el levantamiento del fondo (uplift), causado por presiones ascendentes que superan el peso del suelo en la base de la excavación, y una reducción general de la estabilidad del suelo, que puede provocar fallos en los taludes. Este manual recopila las lecciones aprendidas durante el programa de reconstrucción de la infraestructura de Christchurch (SCIRT), en el que la gestión del agua subterránea en condiciones geotécnicas complejas y tras el sismo fue un desafío diario y crítico para el éxito del proyecto. Estos fenómenos no solo suponen una amenaza para la seguridad de los trabajadores, sino que también pueden ocasionar daños en infraestructuras adyacentes y provocar retrasos y sobrecostes considerables.

1.2. Propósito y alcance del manual.

El manual proporciona una guía práctica y un proceso normalizado para evaluar, seleccionar, diseñar y monitorizar los sistemas de drenaje en obras de construcción. Con base en las enseñanzas extraídas de proyectos de infraestructura complejos, este documento pretende dotar a los ingenieros y gerentes de proyecto de las herramientas necesarias para prever y gestionar los desafíos relacionados con el nivel freático. El objetivo final es reducir los costes y los retrasos asociados a problemas imprevistos mediante una planificación proactiva y un diseño técnico riguroso de las obras temporales de drenaje.

Este manual aborda el ciclo completo de la gestión del agua subterránea en la construcción e incluye:

El contexto geológico y su influencia directa en las estrategias de desagüe.
Los sistemas de control del nivel freático disponibles, sus aplicaciones y limitaciones.
La mitigación de los efectos ambientales y el cumplimiento de las normativas vigentes.
Un marco para la evaluación sistemática de riesgos y la planificación de contingencias.

El documento se centra principalmente en los métodos de control del nivel freático, que consisten en interceptar y extraer el agua subterránea mediante bombeo. También se mencionan brevemente los procedimientos de contención, como las tablestacas o los muros pantalla, que buscan bloquear el flujo de agua hacia la excavación.

Figura 3. Combinación de pantallas con (a) bombeo convencional o (b) barreras horizontales. Adaptado de Cashman y Preene (2012)

1.3. Importancia del contexto geológico.

Análisis de acuíferos: una comprensión fundamental de la hidrogeología del emplazamiento es el pilar de cualquier diseño de un drenaje. Es crucial identificar la naturaleza de los acuíferos presentes, ya sean confinados, no confinados o artesianos. La fuente del agua (por ejemplo, la infiltración de lluvia o la recarga de un río) y la presión a la que se encuentra determinan directamente la selección y la eficacia del sistema de drenaje. Por ejemplo, un acuífero confinado o artesiano puede ejercer una presión ascendente significativa, lo que requiere métodos de control más robustos que los de un simple acuífero no confinado. Este conocimiento también es importante para planificar y evitar impactos no deseados en el entorno, como la afectación de pozos de agua cercanos o la inducción de asentamientos en estructuras adyacentes.
Análisis del perfil del suelo: el comportamiento del agua subterránea está intrínsecamente ligado a las propiedades del suelo. La permeabilidad del suelo, es decir, su capacidad para permitir el paso del agua, es el factor más crítico, ya que determina la facilidad con la que se puede extraer agua mediante bombeo.
- Gravas y arenas limpias: son altamente permeables y ceden agua con facilidad, pero pueden generar grandes caudales de entrada.
- Limos y arcillas: presentan baja permeabilidad, ceden agua muy lentamente y son susceptibles a la consolidación y al asentamiento cuando se reduce la presión del agua.
- Suelos estratificados: la presencia de capas alternas de alta y baja permeabilidad puede crear condiciones complejas, como acuíferos colgados, que requieren un diseño cuidadoso para su drenaje eficaz.
Síntesis de los desafíos geotécnicos: la interacción entre la geología local y las actividades de construcción genera una serie de desafíos específicos que deben anticiparse.

Tabla 1: Desafíos geotécnicos comunes y sus implicaciones.

Desafío geotécnico	Implicaciones para las operaciones de drenaje
Presencia de turba y suelos orgánicos	Estos suelos tienen un alto contenido de agua y son muy compresibles. El drenaje puede provocar asentamientos significativos y dañar la infraestructura cercana. Por ello, es necesario realizar una evaluación de riesgos muy cuidadosa y un seguimiento de los asentamientos.
Gravas superficiales	Las capas de grava poco profundas pueden complicar la instalación de sistemas como los well-points y generar volúmenes de entrada de agua muy elevados que superen la capacidad de los sistemas de bombeo estándar.
Riesgo de encontrar condiciones artesianas	La intercepción de un acuífero artesiano puede provocar un flujo de agua incontrolado hacia la excavación, lo que conlleva un riesgo de inundación, levantamiento del fondo y fallo catastrófico. Por ello, es necesario realizar una investigación geotécnica exhaustiva y elaborar un plan de contingencia robusto.
Niveles freáticos variables	Los niveles freáticos pueden fluctuar estacionalmente o en respuesta a eventos de lluvia. El diseño debe ser capaz de manejar el nivel freático más alto esperado, considerando que las variaciones estacionales en Christchurch pueden alcanzar hasta 3 metros.

Por lo tanto, la comprensión profunda del contexto geológico es el primer paso indispensable para realizar una evaluación sistemática de los riesgos y diseñar un sistema de control del nivel freático adecuado.

2.0 Evaluación previa a la construcción y al análisis de riesgos.

2.1 La fase crítica de planificación.

La fase previa a la construcción ofrece la oportunidad más rentable para identificar, analizar y mitigar los riesgos asociados al drenaje de aguas subterráneas. Una evaluación rigurosa en esta etapa permite diseñar adecuadamente las obras temporales, evitar fallos durante la ejecución y realizar una asignación presupuestaria precisa, lo que evita sobrecostos y retrasos imprevistos. Aunque un diseño proactivo suponga una inversión inicial, casi siempre resulta un ahorro global para el proyecto.

2.2 Pasos clave para el diseño del drenaje.

Desarrollo del modelo geotécnico: para diseñar un control del nivel freático eficaz, es esencial construir un modelo conceptual del subsuelo. Este proceso debe ser dirigido por un técnico competente y consta de los siguientes pasos:

1. Revisión de estudios previos: consultar fuentes de información existentes como mapas geológicos, bases de datos geotécnicas, investigaciones previas en la zona y fotografías aéreas.
2. Evaluación de la permeabilidad: utilizar la información disponible para estimar preliminarmente la permeabilidad de las diferentes capas del suelo.
3. Evaluación de riesgos inicial: realizar una evaluación de alto nivel sobre la posible presencia de suelos o aguas subterráneas contaminadas, la probabilidad de encontrar grava a poca profundidad y el riesgo de que haya condiciones artesianas.
4. Decisión sobre investigaciones adicionales: en función de la complejidad y el perfil de riesgo del proyecto, se debe determinar si la información existente es suficiente o si se requieren investigaciones de campo específicas (por ejemplo, sondeos o ensayos de permeabilidad) para definir adecuadamente el modelo del terreno.

Técnicas para determinar la permeabilidad: la permeabilidad es el parámetro clave que guía el diseño del control del nivel freático. La siguiente tabla resume los métodos disponibles para su determinación, ordenados aproximadamente por coste y fiabilidad.

Método	Descripción	Aplicabilidad	Coste y fiabilidad relativa
1. Empírico (registros de sondeo)	Se asignan valores de permeabilidad basados en las descripciones de los suelos obtenidas de los registros de perforación, que se comparan con valores típicos de referencia.	Útil para evaluaciones preliminares y proyectos de bajo riesgo.	Coste: el más bajo (solo horas de diseño). Fiabilidad: baja; solo proporciona un orden de magnitud.
2. Empírico (método de Hazen)	Estimación de la permeabilidad a partir de las curvas de distribución granulométrica del suelo.	Aplicable solo si se cuenta con ensayos de granulometría en suelos arenosos.	Coste: bajo si los datos ya existen; de lo contrario, requiere muestreo y ensayos de laboratorio. Fiabilidad: baja a moderada.
3. Ensayo de laboratorio (carga constante)	Mide el flujo de agua a través de una muestra de suelo bajo un gradiente hidráulico constante.	Adecuado para suelos con permeabilidades relativamente altas (10⁻² a 10⁻⁵ m/s), como arenas y gravas.	Coste: relativamente bajo, pero requiere la obtención de muestras inalteradas. Fiabilidad: moderada, pero puede no ser representativa de la masa de suelo a gran escala.
4. Ensayo de laboratorio (consolidación/triaxial)	Mide la permeabilidad como parte de ensayos de consolidación o de ensayos triaxiales.	Adecuado para suelos de baja permeabilidad (≤ 10⁻⁶ m/s), como los limos y las arcillas.	Coste: relativamente bajo, pero requiere muestras inalteradas. Fiabilidad: moderada, sujeta a las mismas limitaciones que el ensayo de carga constante.
*5. Ensayo de carga instantánea (slug test)*	Se induce un cambio rápido en el nivel del agua en un pozo o piezómetro y se mide la velocidad de recuperación del nivel.	Realizado in situ en la zona saturada. Puede ser demasiado rápido para suelos muy permeables.	Coste: menor que el de un ensayo de bombeo. Fiabilidad: Proporciona una indicación de la permeabilidad local alrededor del pozo, pero no a escala de sitio.
6. Ensayo de bombeo	Se bombea agua desde un pozo a un caudal constante y se mide el abatimiento del nivel freático en el pozo de bombeo y en pozos de observación cercanos.	Proporciona datos a gran escala y es adecuado para proyectos de desagüe profundos o de larga duración.	Coste: el más alto y el que consume más tiempo (dura de 24 horas a 7 días). Fiabilidad: la más alta, ya que mide la respuesta del acuífero a una escala representativa de las condiciones reales del proyecto.

2.3 Metodología de evaluación de riesgos

Puntuación de riesgos: Para estandarizar el nivel de análisis y supervisión requerido, se propone un sistema de puntuación de riesgos, desarrollado y probado durante el programa SCIRT, que categoriza cada proyecto de control del nivel freático. Este enfoque permite asignar los recursos de diseño de manera proporcional al riesgo identificado, de modo que los proyectos de alta complejidad reciben la atención de especialistas y los de bajo riesgo pueden gestionarse mediante prácticas normalizadas.
Matriz de categorización de riesgos: el número de categoría de riesgo (RCN) se calcula multiplicando las puntuaciones asignadas a seis áreas de riesgo clave (RCN = A x B x C x D x E x F), tal y como se muestra en la siguiente tabla:

A: Profundidad de excavación	Puntuación	B: Agua subterránea	Puntuación	C: Condiciones del terreno	Puntuación
< 2 m	1	No se requiere abatimiento	0	Suelos competentes sin necesidad de soporte temporal	1
2 – 3 m	2	Abatimiento < 1 m requerido	1	Limos y arcillas de baja permeabilidad	2
3 – 6 m	6	Abatimiento 1 – 3 m requerido	2	Arenas limosas	3
6 – 15 m	10	Abatimiento 3 – 6 m requerido	5	Turba y suelos orgánicos	3
> 15 m	12	Influencia en cuerpos de agua superficial	7	Intercepta gravas de moderada a alta permeabilidad	6
		Abatimiento > 6 – 9 m requerido	10	Arenas fluidas	10
		Intercepta acuífero artesiano	10	Suelos contaminados	10
		Agua subterránea contaminada	10
D: Duración del drenaje	Puntuación	E: Coste de componentes del proyecto influenciados por el drenaje	Puntuación	F: Efectos en servicios, infraestructuras y propiedades adyacentes	Puntuación
Excavación abierta por 1 – 2 días	1	< $0.1M	1	Sitio sin construcciones	1
Excavación abierta < 1 semana	2	$0.1M a $0.5M	2	Vía local	2
Excavación abierta por 1 – 4 semanas	3	$0.5M a $1M	3	Vía arterial principal o secundaria	3
Excavación abierta por 1 – 6 meses	4	$1M a $5M	4	Propiedad privada a una distancia menor que la altura de la excavación o estructuras adyacentes sobre pilotes	3
Excavación abierta > 6 meses	5	> $5M	5	Autopista	4
				Vías férreas	4
				Estructuras históricas con cimentaciones superficiales	4
				Infraestructura crítica vulnerable a asentamientos	5

Nota: El Número de Categoría de Riesgo (RCN) se calcula como el producto de las puntuaciones de las 6 áreas (A x B x C x D x E x F).

Niveles de acción de diseño recomendados: una vez calculado el RCN, la siguiente tabla define las acciones mínimas de diseño que deben llevarse a cabo.

Número de categoría de riesgo (RCN)	Consecuencia del riesgo	Acciones mínimas de diseño recomendadas
0 – 10	Bajo	• No se requiere un estudio de drenaje específico para el proyecto. • Implementar el sistema de control del nivel freático basado en la experiencia local previa.
11 – 75	Medio	• Realizar un estudio de escritorio de alto nivel para evaluar las condiciones del terreno y los riesgos de drenaje. • Seleccionar métodos de control de nivel freático apropiados considerando restricciones y riesgos. • Realizar cálculos manuales simples para verificar la idoneidad del diseño de las obras temporales.
76 – 2,500	Alto	• Realizar un estudio de escritorio detallado. • Confirmar las condiciones del terreno y la granulometría mediante al menos un sondeo. • Realizar cálculos de diseño de drenaje (de simples a complejos según corresponda). • Desarrollar e implementar un plan de control de asentamientos simple si es necesario. • Controlar de cerca los sólidos en suspensión durante la descarga.
2,500 – 187,500	Muy Alto	• Revisar un informe geotécnico detallado. • Contratar a un técnico cualificado y experimentado para brindar asesoramiento profesional. • Realizar investigaciones de campo adicionales (p. ej., ensayos de permeabilidad, ensayos de bombeo). • Desarrollar e implementar un plan de control de asentamientos. • Realizar inspecciones de la condición de las propiedades adyacentes antes de comenzar los trabajos.

Una vez evaluado el riesgo y definido el nivel de diseño requerido, el siguiente paso es comprender en detalle las prácticas y metodologías de drenaje disponibles para su ejecución en campo.

3.0 Métodos y prácticas de control del nivel freático

3.1 Introducción a las metodologías

Los métodos de control del nivel freático más comunes en la construcción se basan en la extracción de agua del subsuelo para reducir dicho nivel. La elección del método más adecuado es una decisión técnica que depende fundamentalmente de las condiciones del suelo, la profundidad de la excavación, el caudal de agua previsto y los objetivos específicos del proyecto. Cada método tiene sus propias ventajas y limitaciones, que deben evaluarse cuidadosamente.

3.2 Bombeo desde sumideros

Descripción y aplicación: el bombeo desde sumideros es el método más simple y, a menudo, el más económico. Consiste en excavar zanjas o pozos (sumideros) en el punto más bajo de la excavación para que el agua subterránea fluya por gravedad hacia ellos y, desde allí, sea bombeada y evacuada. Este método es efectivo en suelos con permeabilidad alta o moderada, como las gravas y las arenas gruesas. Su principal limitación es que el agua fluye hacia la excavación antes de ser controlada, lo que puede causar inestabilidad en los taludes y en el fondo. Existe un alto riesgo de tubificación (piping) y de arrastre de finos, lo que puede provocar asentamientos y generar una descarga de agua cargada de sedimentos que requiere un tratamiento exhaustivo.

Requisitos de diseño e instalación: para que un sumidero sea eficaz, debe cumplir los siguientes requisitos:

Profundidad: Suficiente para drenar la excavación y permitir la acumulación de sedimentos sin afectar la toma de la bomba.
Tamaño: Mucho mayor que el de la bomba para facilitar la limpieza y el mantenimiento.
Filtro: El sumidero debe estar protegido con una tubería ranurada o perforada, rodeada de grava gruesa (20-40 mm) para evitar la succión de partículas finas del suelo.
Acceso: Debe permitir la retirada de las bombas para el mantenimiento y la limpieza periódica de los sedimentos acumulados.

Como mejor práctica, se recomienda sobreexcavar el fondo del sumidero y rellenarlo con material grueso para elevar la entrada de la bomba y minimizar la movilización de partículas finas.

Figura 4. Esquema de sumidero y bomba de achique para pequeñas excavaciones, basado en Powers (1992).

Análisis comparativo

Ventajas	Inconvenientes
• Coste relativamente bajo.	• Moviliza sedimentos del terreno, lo que requiere tratamiento de la descarga.
• Equipos móviles y fáciles de instalar y operar.	• No puede utilizarse en «arenas fluidas».
• Solo opera durante los trabajos de construcción.	• Tiene un alto potencial de liberar sedimentos en el medio ambiente y es el método más común para incumplir las condiciones de los permisos ambientales.

3.3 Sistemas de well-points

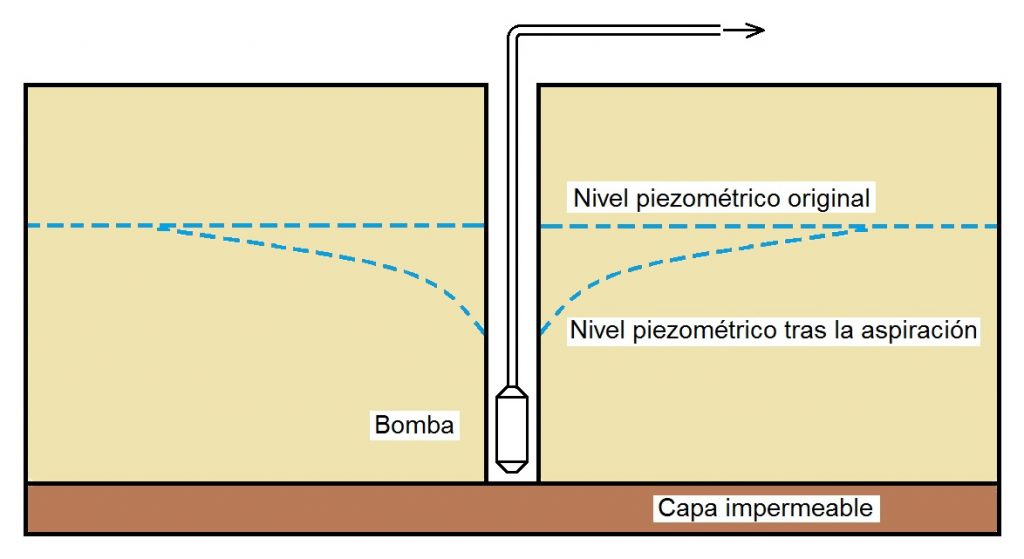
Descripción y aplicación: un sistema de well-points consiste en una serie de tubos de pequeño diámetro (aproximadamente 50 mm) con una sección ranurada en el extremo inferior. Estos tubos se instalan en el terreno a intervalos regulares. Estos tubos, también denominados «puntas de lanza», se conectan a un colector principal, que, a su vez, está conectado a una bomba de vacío. La bomba crea un vacío en el sistema que extrae el agua del subsuelo.

Este método es particularmente efectivo en arenas o suelos con capas de arena. Su principal limitación es la altura de succión, que en condiciones cercanas al nivel del mar es de hasta 8 metros. Para excavaciones más profundas, sería necesario utilizar sistemas escalonados en las bermas.

Consideraciones de diseño

Espaciamiento: el espaciamiento entre los pozos de extracción (que suele oscilar entre 0,6 y 3 m) depende de la permeabilidad del suelo, de la geometría de la excavación y del abatimiento requerido. Cuanto más permeable es el suelo, menor debe ser el espaciamiento.
Paquetes de filtro: en suelos finos o estratificados, es crucial instalar un paquete de filtro (generalmente, arena de textura media a gruesa) alrededor de cada pozo de extracción. Así se evita el bombeo de finos y se crea una ruta de drenaje vertical más eficiente.

Figura 5. Componentes del sistema. Cortesía de ISCHEBECK. http://www.ischebeck.es/assets/wp-content/uploads/agotamiento_agua/Cat%C3%A1logo%20Wellpoint%2016022012.pdf

Análisis comparativo

Ventajas	Inconvenientes
• Descarga limpia: Una vez establecido, el sistema extrae agua limpia que requiere poco o ningún tratamiento.	• El desagüe debe realizarse muy cerca del área de trabajo.
• Abatimiento localizado del nivel freático, lo que resulta en menores volúmenes de descarga.	• Funciona mejor en suelos uniformes.
	• La instalación puede ocupar un espacio considerable en el entorno vial.
	• Requiere experiencia para una instalación y colocación efectivas.
	• Potencial de rendimiento (caudal) y de abatimiento limitados por la altura de succión.

3.4 Pozos de bombeo profundo (dewatering wells)

Descripción y aplicación: los pozos de bombeo profundo son pozos perforados de mayor diámetro y profundidad que los well-points y están equipados con una bomba sumergible. Se trata de un sistema de ingeniería que debe ser diseñado por un especialista. Cada pozo incluye componentes clave, como una rejilla dimensionada para el terreno, un paquete de filtro diseñado específicamente y un sello anular en la superficie para evitar la recarga superficial.

Este método es adecuado para excavaciones grandes, profundas o de larga duración y puede manejar grandes caudales de agua.

Consideraciones de diseño: el diseño de un sistema de pozos profundos requiere un análisis detallado de los siguientes parámetros:

Profundidad y diámetro del pozo: el diámetro debe ser suficiente para alojar la bomba necesaria y la profundidad debe ser significativamente mayor que el abatimiento deseado.
Tamaño de la ranura de la rejilla: se diseña en función del tamaño de grano del suelo o del material filtrante para maximizar la entrada de agua y minimizar la entrada de partículas finas.
Diseño del filtro: el filtro granular que rodea la rejilla es fundamental para evitar que los materiales finos del acuífero migren hacia el pozo.
Distancia entre pozos: Los pozos se espacian típicamente entre 10 y 50 metros. Su diseño es complejo, ya que se basa en la interacción entre los conos de abatimiento de cada pozo.

Figura 6. Agotamiento profundo del nivel freático mediante un pozo filtrante. Elaboración propia basado en Pérez Valcárcel (2004).

Análisis comparativo

Ventajas	Inconvenientes
• Ideal para excavaciones de gran envergadura y proyectos de larga duración.	• Si se extrae más agua de la necesaria, puede afectar a un área mayor de la prevista, lo que puede causar problemas de asentamiento en suelos compresibles (por ejemplo, turba).
• Descarga limpia una vez que el pozo está desarrollado correctamente.	• Puede requerir un tiempo de preparación más largo para lograr el abatimiento del nivel freático.
• Alta capacidad de bombeo, superando problemas de variabilidad del suelo.	• Se requiere un mayor nivel de diseño, planificación y ensayos de campo, como los ensayos de bombeo.
• Puede instalarse fuera del área de trabajo directa, liberando espacio en las zonas congestionadas.
• Las bombas sumergibles son mucho más silenciosas, ideales para áreas sensibles al ruido.

Tras describir los métodos individuales, el siguiente paso lógico es proporcionar una guía clara para seleccionar el sistema más apropiado para cada situación en el campo.

4.0 Selección del método apropiado

4.1 Una decisión estratégica

La elección del sistema de control del nivel freático adecuado es una decisión estratégica que debe equilibrar la eficacia técnica, el coste de implementación y de operación y el impacto ambiental potencial. Una elección informada no se basa en la intuición, sino en la recopilación y el análisis de datos específicos del emplazamiento. Una elección incorrecta puede provocar un rendimiento deficiente, sobrecostes y retrasos significativos en el proyecto.

4.2 Datos clave para la decisión

Para tomar una decisión fundamentada sobre el método de drenaje, es imprescindible recopilar la siguiente información:

Perfil y tipo de suelo, incluyendo la permeabilidad de cada estrato.
Dimensiones de la excavación: ancho, largo y profundidad.
Nivel freático existente, así como el nivel al que se necesita bajar (abatimiento requerido).
Método de excavación y soporte propuesto: por ejemplo, taludes abiertos o tablestacas.
Proximidad a estructuras existentes, cursos de agua y otras infraestructuras sensibles.

4.3 Matriz de decisión

La siguiente tabla sirve de guía para seleccionar una metodología de drenaje según el tipo de suelo predominante.

Guía para la selección de métodos de drenaje según el tipo de suelo.

Tipo de suelo	Tasa de flujo de agua subterránea	Posibles problemas	Metodología de drenaje recomendada
Gravas / cantos	Alta	Se requieren grandes flujos de agua que pueden provenir de pozos profundos para excavaciones profundas o de sumideros para excavaciones superficiales.	Pozos de bombeo profundo y de bombeo desde sumideros.
Arena	Baja a media	Baja estabilidad de la zanja si se permite que la arena fluya hacia la excavación (arena fluida).	Sistemas well-point.
Limo	Baja	Estabilidad variable y bajo rendimiento de agua, lo que puede requerir un espaciado muy reducido de las puntas de lanza y provocar perching localizado.	Sistemas de puntas de lanza (well-pointing) y de bombeo desde sumideros.
Arcilla	Muy baja	Se han detectado problemas mínimos de estabilidad de la zanja y una posible formación de un nivel freático colgado localizado.	Sistemas de puntas de lanza (well-pointing) y de bombeo desde sumideros.
Turba	Variable (baja a alta)	El drenaje puede provocar la compresión de las capas, lo que provoca asentamientos y daños en los terrenos y en la infraestructura circundantes.	Se requiere asesoramiento especializado.
Suelos mixtos	Variable (baja a alta)	La metodología se basa generalmente en el tipo de suelo predominante y en la unidad geológica que presenta el mayor rendimiento hídrico.	Depende de la hidrogeología y de la unidad geológica de mayor rendimiento hídrico.

4.4 Criterios de aplicación específicos

Condiciones que favorecen el bombeo desde sumideros (sump pumping):
- Suelos como grava arenosa bien graduada, grava limpia o arcilla firme o rígida.
- Acuífero no confinado.
- Se requiere un abatimiento moderado y no hay fuentes de recarga cercanas (por ejemplo, un arroyo).
- La excavación tiene taludes poco pronunciados o está protegida por tablestacas hincadas a gran profundidad.
- Cargas de cimentación ligeras.
Condiciones que favorecen los sistemas well-point:
- Suelos arenosos o interestratificados que incluyan arenas (permeabilidad k = 10⁻³ a 10⁻⁵ m/s).
- Acuífero no confinado.
- Se requiere un abatimiento de 5 metros o menos (o de hasta 10 metros si el área de excavación es grande y permite sistemas escalonados).
Condiciones que favorecen la instalación de pozos de bombeo profundo (wells):
- Las condiciones del terreno son demasiado permeables como para que los well-points sean viables.
- Suelos limosos que requieren un diseño de filtro preciso.
- Se requiere un abatimiento de más de 8 metros o un abatimiento en un área extensa durante un período prolongado.
- El acceso a la excavación está restringido o el lugar está congestionado (los pozos pueden ubicarse fuera de las zonas de trabajo).

Independientemente del método elegido, es imperativo gestionar los impactos ambientales asociados, un aspecto crucial que se detallará en la siguiente sección.

Figura 7. Selección del método de drenaje adecuado.

5.0 Mitigación de efectos ambientales y gestión de impactos

5.1 Responsabilidad ambiental y cumplimiento normativo

La gestión del agua subterránea no termina con su extracción, sino que conlleva la responsabilidad de cumplir con la normativa medioambiental y minimizar cualquier impacto negativo en el entorno. Una planificación cuidadosa debe abordar dos aspectos principales: la gestión de la calidad del agua de descarga para proteger los cuerpos de agua receptores y la prevención del asentamiento del terreno, que podría dañar la infraestructura y las propiedades adyacentes.

5.2 Gestión de la calidad del agua extraída

Sólidos en suspensión totales (TSS): el agua bombeada desde una excavación, especialmente desde sumideros, a menudo presenta una alta concentración de sedimentos. La normativa medioambiental exige que esta agua sea tratada para eliminar los sólidos antes de su vertido. Por ejemplo, muchos permisos establecen un límite de 150 g/m³ de TSS. Para el control in situ, una herramienta práctica es la evaluación visual comparativa. En un laboratorio, se pueden preparar muestras estándar con concentraciones conocidas de TSS (por ejemplo, 150 g/m³), que sirven como referencia visual para compararlas rápidamente con las muestras de descarga tomadas en el lugar, lo que permite tomar medidas correctivas inmediatas en caso de observar una turbidez excesiva.
Agua subterránea contaminada: existe el riesgo de encontrar contaminantes en el agua subterránea, especialmente en áreas urbanas o industriales con un historial de actividades potencialmente contaminantes. Durante la fase de planificación, es crucial identificar las zonas de riesgo. Si el proyecto se ubica en una de estas zonas o si se sospecha de contaminación, deberán realizarse muestreos específicos del agua subterránea para analizar la presencia y concentración de contaminantes. Así se puede planificar un sistema de tratamiento adecuado si fuera necesario.

5.3 Métodos de tratamiento de la descarga

Los tanques de sedimentación son el método principal y más común para tratar la descarga. Su principio de funcionamiento es sencillo: reducir la velocidad del flujo de agua para que las partículas de sedimento se asienten por gravedad. Un diseño eficaz incluye cuatro zonas funcionales:

Zona de entrada: Distribuye el flujo de manera uniforme para evitar turbulencias.
Zona de asentamiento: El área principal donde ocurre la sedimentación.
Zona de recolección: El fondo del tanque donde se acumulan los sedimentos.
Zona de salida: Recolecta el agua clarificada para su descarga.

El dimensionamiento adecuado del tanque es fundamental y debe basarse en el caudal de bombeo y el tamaño de las partículas a eliminar.

Otros métodos

Filtrado a través de la vegetación: El agua se descarga sobre una superficie cubierta de vegetación densa (por ejemplo, césped), que actúa como un filtro natural. Este método solo es adecuado como tratamiento secundario tras un tanque de sedimentación.
Bolsas de control de sedimentos: Se trata de bolsas de geotextil que se conectan a la salida de la bomba y filtran los sedimentos. Son útiles para caudales bajos y áreas pequeñas, pero pueden obstruirse rápidamente ante altas concentraciones de sedimentos.

5.4 Control del asentamiento del terreno

Causas y riesgos: El abatimiento del nivel freático puede provocar asentamientos del terreno por tres mecanismos principales:

Aumento de la tensión efectiva: al descender el nivel freático, disminuye la presión del agua en los poros del suelo, lo que incrementa la carga que puede soportar el esqueleto sólido del suelo. Esto provoca su compresión y el consiguiente hundimiento de la superficie.
Pérdida de finos: Un diseño de filtro inadecuado o velocidades de flujo excesivas pueden arrastrar partículas finas del suelo y generar vacíos, lo que provoca asentamientos localizados.
Inestabilidad de los taludes: una reducción insuficiente de las presiones de poro o un control inadecuado de las filtraciones puede comprometer la estabilidad de los taludes de la excavación, lo que provoca fallos localizados y desprendimientos de material.

Los suelos blandos y de baja permeabilidad, como los limos, las arcillas y los suelos orgánicos (turba), son los más susceptibles a sufrir asentamientos significativos por consolidación.

Estrategias de mitigación: Para minimizar el riesgo de asentamientos perjudiciales, deben implementarse las siguientes estrategias:

Diseño adecuado de los filtros: hay que asegurarse de que los filtros de pozos o well-points estén correctamente dimensionados para retener las partículas del suelo.
Control de finos: controlar la cantidad de sólidos disueltos en el agua de descarga. Un aumento sostenido puede indicar una posible pérdida de material del subsuelo.
Control del radio de influencia: diseñar el sistema para limitar la bajada del nivel freático más allá de los límites de la zona, utilizando, si es necesario, barreras de corte o pozos de reinyección.
Control de los asentamientos en el terreno: implementar un plan de supervisión para detectar cualquier movimiento del terreno.

Control de asentamientos: Se debe establecer un plan de supervisión que incluya la instalación de marcadores topográficos en edificios y estructuras cercanos. Es fundamental contar con un punto de referencia estable ubicado fuera de la zona de influencia del drenaje. Se deben establecer umbrales de alerta y de actuación para los asentamientos medidos. Si se alcanzan estos umbrales, se deben adoptar medidas correctivas que pueden ir desde la modificación del funcionamiento de la estación de bombeo hasta la interrupción total del drenaje.

La gestión proactiva de estos riesgos operativos y medioambientales debe complementarse con la preparación ante eventos inesperados, lo que nos lleva a la planificación de contingencias.

6.0 Planificación de contingencias: intercepción accidental de acuíferos artesianos

6.1 Preparación para lo imprevisto.

A pesar de una planificación y ejecución cuidadosas, siempre existe la posibilidad de toparse con condiciones geológicas imprevistas, como la intercepción de un acuífero artesiano o la aparición de caudales de entrada mucho mayores de lo esperado. Estas situaciones pueden escalar rápidamente y provocar un colapso catastrófico de la excavación. Por lo tanto, una preparación adecuada y un plan de respuesta rápida no son opcionales, sino parte esencial de la gestión de riesgos en cualquier proyecto de drenaje.

6.2 Medidas preparatorias

Procedimientos operativos: Antes de iniciar cualquier trabajo de excavación o perforación en zonas de riesgo, se deben establecer los siguientes procedimientos:

Realizar investigaciones geotécnicas adecuadas para identificar la posible presencia de acuíferos artesianos.
Disponer de medios para cerrar rápidamente los pozos de bombeo o las puntas de lanza si se detecta un flujo incontrolado.
Localizar de antemano proveedores de emergencia de materiales como cemento Portland, bentonita y geotextil.
Comprender el procedimiento de cálculo del diseño de la mezcla de lechada para detener el flujo. Se debe medir la carga artesiana y añadir la mezcla de lechada para lograr un equilibrio de presión.
Establecer y distribuir una lista de contactos de emergencia que incluya al ingeniero del proyecto, al contratista de desagüe y a las autoridades ambientales pertinentes.

Equipamiento de emergencia Se debe tener disponible en el sitio el siguiente equipamiento y suministros de emergencia, según el sistema en uso:

Para sistemas well-point:
- Chips de bentonita no recubiertos para el sellado del collar.
- Válvulas para instalar en todas las tuberías de well-points en áreas con sospecha de presión artesiana.
- Equipo de inyección de lechada de cemento y suministros.
- Geotextil y sacos de arena.
Para pozos de bombeo profundo:
- Chips de bentonita no recubiertos para el sellado del collar.
- Obturadores, tubería ascendente, manómetros y accesorios apropiados para cortar el flujo y medir la presión.
- Equipo de inyección de lechada de cemento y suministros.
- Geotextil y sacos de arena.
- Lodo de perforación polimérico para compensar y suprimir flujos artesianos bajos durante la perforación del pozo.

Además, es necesario contar con un teléfono móvil con cámara, secciones de tubería extensibles para medir la altura de la presión artesiana y el diseño de la mezcla de lechada de contingencia.

6.3 Protocolo de implantación y respuesta

Pasos inmediatos: En caso de detectar un flujo de agua incontrolado, se debe seguir el siguiente protocolo de manera inmediata y secuencial:

Evaluar la situación: Determinar si el caudal y la turbidez del agua son constantes o están aumentando. Verificar si el flujo está confinado al pozo o se está extendiendo por la excavación.
Notificar al ingeniero y al gerente del proyecto: Proporcionar una descripción detallada de las condiciones, el caudal estimado y los eventos que llevaron al incidente. Enviar fotografías o videos en tiempo real si es posible.
Notificar a las autoridades pertinentes: Informar a las autoridades ambientales y a otras partes interesadas sobre la situación y las medidas de contención planificadas.

Acciones de emergencia: Una vez notificado el incidente, se pueden tomar una o más de las siguientes acciones de emergencia para controlar la situación:

Rellenar la excavación: Comenzar a rellenarla con material hasta que el peso del relleno sea suficiente para controlar el flujo y el transporte de sedimentos.
Medir la presión artesiana: Utilizar secciones de tubería para medir la altura a la que llega el agua y así determinar la presión del acuífero.
Controlar la descarga: Dirigir cualquier descarga de agua a través de las medidas de control de erosión y sedimentos establecidas en el sitio.
Inundar la excavación: Como medida drástica, rellenar la excavación con agua hasta el nivel freático original para equilibrar las presiones y estabilizar la situación mientras se reconsidera el diseño.

La combinación de una planificación rigurosa, una ejecución cuidadosa y una preparación exhaustiva ante contingencias es la clave para una gestión exitosa y segura del agua subterránea en cualquier proyecto de construcción.

En este audio podéis escuchar una conversación sobre este tema.

Este es un vídeo que resume bien las ideas principales.

Os dejo el documento completo; espero que os sea de interés.

Pincha aquí para descargar

REFERENCIAS:

CASHMAN, P.M.; and PREENE, M. (2012). Groundwater Lowering in Construction: A Practical Guide to Dewatering, 2nd edition. CRC Press, Boca Raton, 645 pp.
HERTZ, W.; ARNDTS, E. (1973). Theorie und praxis der grundwasserabsenkung. Ernst & Sohn, Berlin.
JUSTO ALPAÑES, J.L.; BAUZÁ, J.D. (2010). Tema 10: Excavaciones y drenajes. Curso de doctorado: El requisito básico de seguridad estructural en la ley orgánica de la edificación. Código Técnico de la Edificación. ETS. de Arquitectura, Universidad de Sevilla.
MUZAS, F. (2007). Mecánica del suelo y cimentaciones, Vol. II. Universidad Nacional de Educación a Distancia, Madrid.
POWERS, J.P. (1992). Construction dewatering: New methods and applications. Ed. Wiley et al., New York.
PREENE, M.; ROBERTS, T.O.L.; POWRIE, W. (2016). Groundwater Control – Design and Practice, 2nd Edition. Construction Industry Research and Information Association, CIRIA Report C750, London.
SCHULZE, W.E.; SIMMER, K. (1978). Cimentaciones. Editorial Blume, Madrid, 365 pp.
TOMLINSON, M.J. (1982). Diseño y construcción de cimientos. URMO, S.A. de Ediciones, Bilbao, 825 pp.
YEPES, V. (2020). Procedimientos de construcción de cimentaciones y estructuras de contención. Colección Manual de Referencia, 2ª edición. Editorial Universitat Politècnica de València, 480 pp. Ref. 328. ISBN: 978-84-9048-903-1.

Curso:

Curso de procedimientos de contención y control del agua subterránea en obras de Ingeniería Civil y Edificación

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Guía para principiantes sobre la compactación de suelos.

1. ¿Qué es la compactación y por qué es importante?

La compactación de suelos es el proceso de aumentar la densidad de un terreno aplicando energía mecánica. En términos sencillos, consiste en hacer circular cargas elevadas sobre capas de suelo el número de veces necesario para alcanzar la densidad especificada. Al reducir los vacíos de aire en el suelo, se aumenta su resistencia, se reduce su capacidad de deformación y se disminuye su permeabilidad.

El objetivo principal de la compactación es mejorar las propiedades geotécnicas del suelo para garantizar la seguridad y durabilidad de las estructuras construidas sobre él, como carreteras, edificios o presas. La elección del equipo y del método de compactación no es universal, sino que depende de factores clave como la naturaleza del terreno, su contenido de humedad y la función que desempeñará el relleno compactado.

Para seleccionar y utilizar correctamente estos equipos, es esencial comprender los principios fundamentales que rigen su funcionamiento.

Figura 1. Distintos tipos de compactadores. https://www.noticiasmaquinaria.com/nuevos-modelos-de-la-serie-de-rodillos-tandem-de-hamm-en-conexpo/

2. Los cuatro esfuerzos elementales de la compactación.

Toda la maquinaria de compactación, desde un pequeño pisón manual hasta un rodillo de varias toneladas, aplica una combinación de cuatro esfuerzos básicos para densificar el suelo. Comprender estos mecanismos es el primer paso para dominar el proceso.

Tipo de esfuerzo	Mecanismo y efecto principal
Estático vertical	Aplica el peso de la máquina para comprimir el suelo. Produce tensiones fundamentalmente verticales que aprietan las partículas entre sí.
Amasado	Genera tensiones en múltiples direcciones, «amasando» el suelo para reordenar partículas. Es especialmente útil para romper terrones en suelos cohesivos.
Impacto	Aplica una fuerza súbita que propaga una onda de presión, alcanzando mayor profundidad que el esfuerzo estático.
Vibratorio	Aplica una sucesión rápida de impactos que reduce la fricción interna entre partículas, facilitando su reacomodo en una configuración más densa.

Es importante destacar que el tipo de esfuerzo aplicado influye directamente en la estructura final de las partículas del suelo. Un terreno más compactado presenta partículas más orientadas y ordenadas (menos «floculadas»). El efecto de ordenamiento es progresivamente mayor al aplicar esfuerzos en el siguiente orden: estático, vibratorio, de impacto y, por último, de amasado.

Ahora que conocemos la teoría que hay detrás de la compactación, podemos explorar los equipos que aplican estos esfuerzos en la práctica.

3. Tipos principales de equipos de compactación.

Los equipos de compactación se pueden clasificar según el principio de trabajo predominante que utilizan: la fuerza estática de su propio peso o la energía dinámica de la vibración.

3.1. Compactadores estáticos: la fuerza del peso.

Estos equipos dependen principalmente de su peso para compactar el suelo.

3.1.1. Apisonadoras de rodillos lisos

Principio de funcionamiento: utilizan cilindros metálicos lisos para aplicar presión estática. Su mecanismo de compactación es «de arriba hacia abajo», por lo que la capa superior recibe la mayor energía.
Suelos adecuados: arenas y gravas bien graduadas, limos y arcillas de baja plasticidad. No se recomiendan para arenas uniformes o arcillas blandas.
Limitación principal: existe el riesgo de compactar en exceso la superficie y crear una costra rígida conocida como «encarpetamiento», mientras que las capas inferiores quedan menos densas.

Figura 2. Apisonadora estática de rodillo liso tipo triciclo. Imagen: V. Yepes

3.1.2. Compactadores de patas apisonadoras («pata de cabra»)

Principio de funcionamiento: en lugar de un rodillo liso, utilizan cilindros con múltiples «patas» o salientes que penetran en el suelo. Esto concentra la presión y compacta el terreno «de abajo hacia arriba».
Suelos adecuados: son especialmente efectivos en arenas y gravas con más del 20% de finos, así como en la mayoría de los suelos de grano fino (suelos limo-arcillosos, arenas limosas y arcillosas).
Ventaja principal: la acción de las patas rompe los terrones y grumos del suelo, a la vez que mejora la trabazón (unión) entre las sucesivas capas de material compactado.

Figura 3. Rodillo remolcado pata de cabra. Imagen: V. Yepes (2021)

3.1.3. Compactadores de ruedas neumáticas

Principio de funcionamiento: combinan el esfuerzo estático de su peso con el efecto de amasado que se produce por la deformación de sus neumáticos de goma, un proceso que reordena las partículas sin romperlas ni aplastarlas.
Suelos adecuados: son eficaces en suelos algo cohesivos y rellenos de limos poco plásticos.
Ventaja clave: son muy versátiles. Se puede ajustar su efecto modificando dos variables principales:
- Aumentar la presión de inflado: incrementa la compactación en la superficie.
- Aumentar la carga por rueda: aumenta el efecto de compactación en profundidad.

Figura 4. Compactador con neumáticos con dibujo. http://www.corinsa.es/tecnologia/compactacion/compactacion-de-tierras/

3.2. Compactadores vibratorios: reduciendo la fricción interna

Estos equipos añaden una fuerza dinámica a su peso estático, lo que los hace extremadamente eficientes.

3.2.1. Principio de funcionamiento

Mecanismo: la vibración de un cilindro o una placa, lo que elimina en gran medida la fricción interna entre las partículas del suelo. Así, las partículas se reordenan y alcanzan una mayor densidad con menos esfuerzo y en capas de mayor espesor. Es especialmente eficaz en terrenos granulares (arenas y gravas). Para hacerse una idea de su eficacia, la acción de un rodillo vibrante puede equivaler a la de un rodillo estático mucho más pesado: hasta ocho veces en suelos cohesivos y hasta doce veces en gravas y escolleras.
Regla de oro para su uso:
- Materiales granulares (arenas, gravas): se compactan mejor con frecuencia alta y amplitud reducida.
- Materiales cohesivos (arcillas, limos): prefieren más amplitud y menor frecuencia.

3.2.2. Tipos más comunes

Existen diversos modelos: los monocilíndricos (con rodillo liso o de patas), los de dos rodillos (tándem) y los mixtos (un rodillo y ruedas neumáticas). De todos ellos, los monocilíndricos autopropulsados son los más versátiles en la mayoría de las obras de movimiento de tierras.

Figura 5. Rodillo compactador vibratorio hidráulico de un solo tambor LSD216H. http://changlin.es/3-2-6-hydraulic-road-roller.html

3.3. Equipos para trabajos específicos

Para tareas específicas o en áreas de difícil acceso, se utilizan equipos más especializados.

3.3.1. Placas y pisones vibrantes

Son máquinas de pequeño tamaño que son guiadas por un operario. Su principal ventaja es que pueden trabajar en espacios reducidos a los que no pueden acceder máquinas más grandes, por ejemplo, en la compactación de rellenos en zanjas o trasdoses de muros.

3.3.2. Compactadores por impactos de gran energía

Este sistema es una alternativa más intensa que los rodillos vibratorios convencionales. Utiliza rodillos de perfil irregular (no cilíndricos) que, al girar a gran velocidad, generan impactos de alta energía. Su principal ventaja es la profundidad de su efecto, que puede alcanzar hasta cuatro o cinco metros.

Figura 6. Compactador de impacto de gran energía.

Una vez conocidos los tipos de equipos disponibles, el siguiente paso lógico es aprender a decidir cuál es el más adecuado para cada situación.

4. ¿Cómo elegir el equipo de compactación adecuado?

La elección del compactador no tiene una solución única, ya que depende de múltiples factores y, en última instancia, es una decisión económica. No obstante, para poder tomar una decisión técnica fundamentada, hay que tener en cuenta tres factores determinantes:

La naturaleza del material: es el factor más importante. Los suelos se pueden clasificar en tres grandes grupos:
1. Suelos finos: limos y arcillas.
2. Suelos de grano grueso: arenas y gravas.
3. Pedraplenes: materiales rocosos.
El estado del material: principalmente, su contenido de humedad. La humedad actúa como un lubricante entre partículas, pero un exceso o defecto puede dificultar enormemente la compactación.
El volumen, la forma de la zona a compactar y el ritmo de la obra: Un área grande y abierta permite el uso de máquinas de alto rendimiento. De hecho, suelen elegirse compactadores con una capacidad de producción superior a la de los equipos de excavación y transporte, para evitar que la compactación se convierta en un «cuello de botella» que retrase todo el proyecto.

La siguiente tabla ofrece una guía simplificada para la selección inicial del equipo en función del tipo de suelo.

Guía rápida para la selección de equipos por tipo de suelo.

Tipo de suelo	Equipos recomendados	Consideración clave
Suelos finos (limos y arcillas)	• Compactadores de patas apisonadoras • Compactadores de neumáticos	El control preciso de la humedad es fundamental. Estos suelos son sensibles a un exceso o defecto de agua.
Suelos de grano grueso (arenas y gravas)	• Rodillos vibratorios • Compactadores de neumáticos pesados	La vibración es extremadamente efectiva para reordenar las partículas en este tipo de material.
Pedraplenes (roca)	• Equipos vibratorios pesados (más de 10 toneladas)	Se necesita una gran energía de compactación debido al gran tamaño de los elementos rocosos.

Elegir el equipo adecuado no solo garantiza que se alcancen las especificaciones de densidad, sino que también optimiza el rendimiento y los costes del proyecto.

5. Conclusión: principios clave para el éxito de una compactación.

La compactación es una de las operaciones más importantes en la construcción, ya que de ella dependen la estabilidad y durabilidad de casi cualquier estructura. Aunque se trata de un tema amplio, un principiante puede sentar unas bases sólidas de conocimiento si se centra en dos principios fundamentales.

Para lograr una compactación eficaz, es esencial comprender y dominar los cuatro tipos de esfuerzos básicos (estático, de amasado, de impacto y vibratorio), así como la forma en que cada máquina los aplica.
Además, es importante entender que la elección del equipo depende principalmente del tipo de suelo. No hay una máquina universal: la clave del éxito es adaptar la herramienta al material con el que se trabaja.

Aquí tienes un vídeo introductorio a los compactadores.

A continuación, os dejo un resumen de las ideas más relevantes que un principiante debería conocer sobre la compactación de suelos. Espero que os resulte interesante.

Referencias:

YEPES, V. (1997). Equipos de movimiento de tierras y compactación. Problemas resueltos. Colección Libro Docente nº 97.439. Ed. Universitat Politècnica de València. 253 pág. Depósito Legal: V-4598-1997. ISBN: 84-7721-551-0.

YEPES, V. (2021). Procedimientos de construcción para la compactación y mejora del terreno. Colección Manual de Referencia, 1ª edición. Editorial Universitat Politècnica de València, 426 pp. Ref. 428. ISBN: 978-84-9048-603-0.

YEPES, V. (2022). Gestión de costes y producción de maquinaria de construcción. Colección Manual de Referencia, serie Ingeniería Civil. Editorial Universitat Politècnica de València, 243 pp. Ref. 442. ISBN: 978-84-1396-046-3

YEPES, V. (2023). Maquinaria y procedimientos de construcción. Problemas resueltos. Colección Académica. Editorial Universitat Politècnica de València, 562 pp. Ref. 376. ISBN 978-84-1396-174-3

Cursos:

Curso de compactación superficial y profunda de suelos en obras de ingeniería civil y edificación.

Curso de gestión de costes y producción de la maquinaria empleada en la construcción.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Rotopalas: maquinaria de excavación continua para grandes producciones

Las rotopalas, conocidas en inglés como Bucket Wheel Excavators (BWE), son máquinas de producción continua que integran las funciones de arranque, carga y transporte del material sin interrupciones. Están especialmente diseñadas para excavar materiales de fácil manipulación, como arenas, gravas, margas, arcillas o lignito. Su funcionamiento continuo las hace ideales para explotaciones mineras a cielo abierto, donde se requiere una alta eficiencia operativa en procesos prolongados y repetitivos.

El origen de estas imponentes máquinas se remonta a 1881, en Estados Unidos, cuando se construyó el primer equipo accionado por vapor. Sin embargo, no fue hasta 1916 en Alemania cuando se produjo su verdadero desarrollo industrial, al aplicarse en la explotación de lignito pardo. A partir de la década de 1950, las rotopalas experimentaron una notable evolución técnica, con modelos de mayor capacidad que respondían a las crecientes necesidades de producción. En la actualidad, estas máquinas pueden mover volúmenes superiores a los 254 000 m³ de material, lo que da una idea de su gran capacidad. En comparación, los Bucket Chain Excavators (BCE), aunque útiles en ciertas aplicaciones, apenas superan los 14 000 m³ y se emplean principalmente para retirar recubrimientos.

El diseño de las rotopalas se clasifica según la relación entre la longitud del brazo del rodete (L) y el diámetro del rodete (D). De este modo, se distinguen los modelos compactos (L/D = 2), semicompactos (L/D = 3) y convencionales (L/D = 4). Las compactas presentan varias ventajas significativas: una inversión inicial un 20 % inferior a la de las convencionales, menor peso, mayor estabilidad y tiempos de entrega más reducidos. Sin embargo, su diseño, limitado a dos orugas, restringe su tamaño máximo a 1600 toneladas, lo que implica una capacidad máxima de producción de 7500 m³/h y un brazo más corto que reduce su alcance operativo. Esta clasificación está normalizada por la norma DIN 22266, que define un sistema de denominación mediante letras que representan distintas características del equipo, como, por ejemplo, el tipo de tren de rodaje o la capacidad de los cangilones.

Figura 2. Rotopala semicompacta. Cortesía SKW

Una rotopala está formada por múltiples sistemas clave que permiten su funcionamiento. El tren de rodaje puede montarse sobre vías o, lo que es más habitual en minería a cielo abierto, sobre orugas. La configuración de estas últimas (dos, tres, cuatro, tres dobles o seis dobles) depende del peso de la máquina y de la capacidad portante del terreno. Cada oruga incorpora un bastidor, una rueda motriz o guía elevada, rodillos de sustentación y zapatas. La corona de giro permite orientar el brazo del rodete, cuya longitud influye directamente en la altura máxima de excavación, la anchura del bloque que se va a extraer y la selectividad del corte. El rodete es el elemento encargado de arrancar el material y su diseño depende de las propiedades geomecánicas del macizo rocoso, la resistencia del material y la producción horaria deseada. Su diámetro oscila entre 2,5 y 22 metros, y su capacidad productiva está entre 200 y 19 000 m³/h. Además, cada tonelada adicional en el peso del rodete implica una carga extra de 400 toneladas sobre la estructura de la máquina.

Existen varios tipos de rodete. El tipo celular, muy habitual en los parques de homogeneización, emplea una placa de caída con forma de arco que crea una célula para conducir el material hacia la cinta lateral. El tipo no celular se caracteriza por tener cangilones insertados en un espacio anular, con un cierre radial que permite aumentar la capacidad del cangilón en un 50 %. Por último, el tipo semicircular tiene un cierre inferior con planos inclinados llamados semicelulares y una vertedera fija. Los cangilones pueden tener un respaldo cerrado, que es ideal para materiales adhesivos como las arcillas duras (tipo «caparazón de tortuga»), o un respaldo de cadenas, que es más adecuado para materiales blandos, húmedos o pegajosos. Los elementos de corte, como dientes, cuchillas u orejetas angulares, son determinantes para la eficiencia de la excavación y deben ser fácilmente sustituibles, resistentes a la abrasión y al impacto. En materiales duros, pueden incorporarse precortadores que fragmentan previamente el material, aunque esto puede generar sobrecargas y vibraciones no deseadas.

Figura 3. Bucket Wheel Excavator. Cortesía FAM-BEUMER GROUP.

El sistema de izado permite posicionar el rodete a la altura de operación deseada y realizar descensos o ascensos rápidos mediante cilindros hidráulicos o cables de acero. Por otro lado, la descarga del material excavado se realiza mediante sistemas como puentes de conexión, brazos de descarga o cintas transportadoras, lo que otorga gran flexibilidad al sistema.

El dimensionamiento de una rotopala debe tener en cuenta múltiples factores técnicos. El diámetro del rodete se selecciona en función de la capacidad nominal requerida y de las propiedades del material, procurando elegir el diámetro más pequeño posible que cumpla los objetivos de producción, ya que un rodete de mayor tamaño incrementa el peso y complica la estática de la máquina. La capacidad nominal (Q) distingue entre la producción teórica o de diseño (Q_t) y la producción real, que se ve afectada por factores como el grado de llenado de los cangilones y las paradas por mantenimiento o averías. La producción teórica se calcula mediante la fórmula Q_t = Q_a / (F · horas/día · días/año), donde F es un factor de campo que incluye la eficiencia y las constantes operativas. La producción de material suelto se determina aplicando el esponjamiento del material, que normalmente se sitúa entre 1,3 y 1,6, o mediante la fórmula Q_ts = I * s * 60, donde I es la capacidad del cazo y s el número de descargas por minuto.

El tipo de material que se va a excavar influye en la velocidad de corte, el número de cangilones, el diámetro del rodete y la inclinación del brazo. La velocidad de corte (V_c) se calcula como V_c = ω · D / 2 y suele estar entre 2 y 3,5 m/s, debiendo mantenerse por encima de la velocidad crítica (V_cri = 2,22 · D). El número de cangilones (Z) depende del material: las rocas blandas requieren pocos cangilones grandes, mientras que las rocas duras exigen muchos cangilones pequeños. Como estimación, se puede considerar Z = 4D. La frecuencia de descarga (s) se obtiene mediante la fórmula s = (V_c · Z) / (π · D) · 60, y la capacidad de los cangilones (V) mediante V = (Q_ts · 60) / (s · 1,25). Las potencias necesarias para la excavación, la aceleración, la elevación y el sistema completo deben calcularse en función de la producción deseada, el tipo de material y el diseño mecánico del equipo.

Durante la operación, el rodete gira mientras el brazo se mueve y el corte más eficiente se produce cuando el brazo está perpendicular al frente de trabajo (ángulo α = 0°). El avance puede realizarse en terrazas, donde el rodete desciende escalonadamente tras cada pasada, o en cortes descendentes, bajando con cada inversión del giro del brazo. Existen diversas variantes operativas, como la excavación en bloque lleno, la más común en la actualidad gracias a la movilidad sobre orugas, la excavación en frente largo, en la que la máquina avanza en paralelo al frente, y la excavación en bloque lateral, que es una adaptación del sistema anterior. También es posible excavar por debajo del nivel de las orugas, lo que permite trabajar con bancos de mayor altura con respecto a la posición del tren de rodaje.

Figura 4. Variantes de excavación de la rotopala. Fuente: Manual de arranque, carga y transporte en minería a cielo abierto (1995)

Entre las múltiples ventajas de las rotopalas, destacan su capacidad de excavación continua, su bajo consumo energético (hasta un 70 % menos que los sistemas de cables), la ausencia de impactos durante la carga, su gran radio de vertido y la posibilidad de operar tanto por encima como por debajo del nivel del terreno. Además, pueden trabajar en bancos de distintas alturas, generar taludes estables, entregar material fácilmente transportable por cinta y permitir una gran selectividad en la excavación. También pueden diseñarse para ejercer una baja presión sobre el terreno, lo que resulta clave en zonas con baja capacidad portante.

Sin embargo, no todo son ventajas. Las rotopalas requieren un mantenimiento complejo y frecuente, no son flexibles ante cambios en la geometría o tectónica del yacimiento y no sirven para excavar materiales compactos o muy abrasivos. Además, su rendimiento global depende de la disponibilidad de todos los elementos en serie que componen el sistema, lo que introduce una fuerte interdependencia operativa. Por último, su adquisición e instalación suponen una inversión inicial muy elevada, lo que limita su adopción a proyectos a gran escala y a largo plazo.

En resumen, las rotopalas son una solución de ingeniería impresionante para grandes operaciones mineras, ya que combinan eficiencia, potencia y continuidad operativa. No obstante, no son la herramienta adecuada para todos los contextos y, en las condiciones apropiadas, su rendimiento y productividad son difíciles de igualar.

Os dejo algunos vídeos que espero os interesen:

Referencias:

GÓMEZ DE LAS HERAS, J.; MANGLANO, S.; TOLEDO, J.; LÓPEZ-JIMENO, C.; LÓPEZ-JIMENO, E. (1995). Manual de arranque, carga y transporte en minería a cielo abierto. Instituto Geológico y Minero de España, Madrid, 604 pp.

MARTÍNEZ-PAGÁN, P. (2025). Rotopalas. Apuntes 4º curso GIRME. Universidad Politécnica de Cartagena.

YEPES, V. (1995). Maquinaria de movimiento de tierras. Servicio de Publicaciones de la Universidad Politécnica de Valencia. SP.UPV-264. 144 pp.

YEPES, V. (1997). Equipos de movimiento de tierras y compactación. Problemas resueltos. Colección Libro Docente n.º 97.439. Ed. Universitat Politècnica de València. 256 pág. Depósito Legal: V-4598-1997. ISBN: 84-7721-551-0.

Curso:

Curso de gestión de costes y producción de la maquinaria empleada en la construcción

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Algunas preguntas sobre la gestión y el mantenimiento de la maquinaria empleada en la construcción

¿Cuáles son los objetivos principales del mantenimiento de la maquinaria y cómo se clasifica?

El mantenimiento de la maquinaria de construcción tiene como objetivos fundamentales maximizar su disponibilidad al mínimo coste, optimizar su rendimiento y garantizar unas condiciones óptimas de operatividad y seguridad. Esto se traduce en la reducción de costes debidos a paradas accidentales, minimizando las pérdidas de producción y los gastos propios del mantenimiento, así como en la limitación del deterioro de la maquinaria para evitar la disminución de la calidad del producto.

Las tareas de mantenimiento se clasifican en niveles según la importancia de la obra y sus misiones específicas. Por ejemplo, en una empresa constructora típica, el primer escalón (conductoras y conductores) se encarga del mantenimiento diario, semanal o quincenal (limpieza, repostaje, engrase y reparaciones de urgencia). El segundo escalón (equipos de obra) se encarga del mantenimiento mensual, trimestral o semestral, que incluye revisiones, ajustes ligeros y localización de averías. Los escalones superiores (el tercero y el cuarto, talleres móviles y fijos) se dedican a reparaciones más complejas, a la sustitución de piezas y a grandes reconstrucciones.

¿Qué tipos de políticas de mantenimiento existen y cuál es el más beneficioso a largo plazo?

No existe una clasificación rígida de los sistemas de mantenimiento y cada empresa debe elegir el más adecuado para cada máquina. Sin embargo, pueden clasificarse principalmente en:

Corrección por avería: Se permite que los equipos funcionen hasta que fallen, y luego se reparan lo antes posible. Aunque a corto plazo puede parecer económico, a medio y largo plazo puede generar costes elevados debido a la imposibilidad de programar las paradas y al riesgo de fallos graves, lo que disminuye la eficiencia del servicio. Solo se justifica en contadas ocasiones o cuando se trata de muchas máquinas iguales y hay capacidad de sobra.
Mantenimiento rutinario: Se establecen instrucciones generales para el mantenimiento de grupos homogéneos de máquinas, basado en la experiencia, para prevenir fallos. Es de bajo costo y puede resolver muchas averías antes de que ocurran.
Mantenimiento preventivo planificado: Se establecen ciclos de revisiones y sustituciones de componentes importantes según las instrucciones del fabricante y el uso de la máquina. Esto permite registrar averías y prever la vida útil de los elementos. Aunque es más costoso a corto plazo, resulta más ventajoso a medio y largo plazo, ya que permite programar los tiempos de inactividad y evitar fallos catastróficos, lo que aumenta la eficacia general. El objetivo es reparar antes de que se produzca una avería importante, lo que resulta más rápido y económico.

En resumen, el mantenimiento preventivo planificado es el más ventajoso a medio y largo plazo, ya que permite anticiparse a los problemas, reducir los costes y los tiempos de reparación, y aumentar la eficacia del servicio.

¿Cómo se distribuye el tiempo de permanencia de una máquina en obra y qué implicaciones tiene para los costos?

El tiempo que una máquina permanece en obra se divide en varias categorías, lo que afecta directamente el costo horario y la producción.

Tiempo de calendario laborable (fondo horario bruto): Horas reconocidas por la legislación laboral y la organización para trabajar.
Tiempo laborable real (fondo horario operacional): Horas de presencia efectiva de la máquina en obra, descontando circunstancias fortuitas como fenómenos atmosféricos, huelgas o catástrofes. Incluye horas extraordinarias.
Tiempo de máquina en disposición (fondo horario de explotación): Horas en las que la máquina está operativa y lista para trabajar, excluyendo paradas menores a 15 minutos.
Tiempo fuera de disposición: Horas en las que la máquina no está operativa, divididas en:
Mantenimiento: Tareas previsibles.
Averías: Reparaciones imprevisibles.
Parada por organización de obra: Tiempo de inactividad por causas ajenas a la máquina (falta de tajo, suministros, averías de otras máquinas, etc.).
Tiempo de trabajo útil: Horas netas donde la máquina produce, incluyendo trabajo productivo y trabajo no productivo o complementario.

Esta distribución temporal implica que el coste horario de una máquina varía en función de la referencia. Para el propietario, el coste se evalúa en relación con la hora de utilización, mientras que, en el caso de un alquiler, se refiere a la hora laborable real. Ampliar la jornada laboral para aumentar las horas útiles puede disminuir el coste horario fijo y acortar los plazos, pero hay que sopesarlo con inconvenientes como el aumento de costes por horas extra del operario, su fatiga y la dilución de responsabilidades si hay varios conductores, lo que puede incrementar las averías.

¿Cómo se calcula la fiabilidad de un equipo de construcción y cuáles son las fases de su vida útil según la «curva de la bañera»?

La fiabilidad se define como la probabilidad de que una unidad funcione correctamente en un intervalo de tiempo determinado sin interrupciones debidas a fallos de sus componentes, en condiciones establecidas. Está relacionada con el tiempo medio entre fallos (TMEF), que es la relación entre las horas de funcionamiento y el número de averías sufridas en ese período.

La «curva de la bañera» describe la evolución de la tasa de fallos de una máquina a lo largo del tiempo y se divide en tres fases:

Período de mortalidad infantil o fallos prematuros: Caracterizado por una alta tasa de fallos que disminuye rápidamente. Las causas suelen ser errores de diseño, fabricación o uso. Estos fallos ocurren en la fase de rodaje y, una vez resueltos, no suelen repetirse.
Período de tasa de fallos constante o vida útil: Los fallos aparecen de forma aleatoria y accidental, debidos a limitaciones de diseño, percances por uso o mal mantenimiento. Es el período ideal de utilización de la máquina.
Período de desgaste: La tasa de fallos aumenta con el tiempo debido a la vejez y el fin de la vida útil. En esta fase, se recomienda el reemplazo preventivo de componentes o incluso la renovación completa del equipo para evitar incidentes catastróficos.

Figura 2. Curva de fiabilidad de una máquina

Para alargar su vida útil, se puede aplicar el envejecimiento preventivo (funcionamiento preliminar para detectar fallos prematuros) y la sustitución preventiva (reemplazo de unidades al finalizar su vida útil para evitar fallos).

¿Cómo se modela la fiabilidad de una máquina y qué técnicas de prevención de fallos se utilizan en el diseño?

La fiabilidad de una máquina puede modelarse mediante la distribución exponencial cuando la tasa de fallos es constante durante el período de vida útil. Esto implica que la ocurrencia de un fallo es imprevisible e independiente de la vida útil del equipo. Una generalización de este modelo es la función de Weibull, que se utiliza cuando la tasa de fallos es variable y permite tener en cuenta las fases de fallos precoces y de envejecimiento.

En lo que respecta a las técnicas de prevención de fallos en el diseño de equipos, las empresas se centran en maximizar la fiabilidad del producto. Algunas metodologías clave son:

Despliegue de la Función de Calidad (QFD): Permite traducir los requisitos de calidad del cliente en características técnicas del producto, utilizando matrices para analizar necesidades, competencia y nichos de mercado.
Análisis Modal de Fallos y Efectos (AMFE): Una metodología estructurada para identificar y prevenir modos de fallo potenciales y sus causas en un producto o sistema.
Análisis del valor: Busca reducir el coste del producto sin eliminar las características esenciales demandadas por los clientes, identificando cambios que aumenten el valor sin un incremento desproporcionado del coste.

¿Cómo influyen las condiciones climáticas y otros imprevistos en la planificación del tiempo de trabajo en una obra de construcción?

Las condiciones climáticas y otros imprevistos son factores cruciales que influyen en el plazo de ejecución de una obra. La planificación del tiempo de trabajo disponible se basa en datos históricos del clima y en el calendario laboral.

El método de la Dirección General de Carreteras, por ejemplo, utiliza coeficientes de reducción aplicados al número de días laborables de cada mes para estimar los días efectivamente trabajados. Estos coeficientes tienen en cuenta:

Temperatura límite: Por debajo de la cual no se pueden ejecutar ciertas unidades de obra (ej., 10 ºC para riegos bituminosos, 5 ºC para mezclas bituminosas, 0 ºC para manipulación de materiales húmedos).
Precipitación límite diaria: Se definen valores como 1 mm/día para trabajos sensibles a lluvia ligera y 10 mm/día para la mayoría de los trabajos, donde una protección especial sería necesaria.

Los días utilizables netos de cada mes se calculan multiplicando los días laborables por los coeficientes reductores por climatología adversa y por los días no laborables, que dependen de festivos y convenios laborales. La reducción de días representa la probabilidad de que un día del mes sea favorable desde el punto de vista climático y laborable. Estos cálculos permiten elaborar un plan de obra lo más ajustado posible, minimizando las desviaciones de plazo, aunque la evolución del tiempo atmosférico es impredecible en la práctica.

¿Qué se entiende por «disponibilidad» de una máquina en obra y cómo se calcula?

La disponibilidad de una máquina se refiere a su estado operativo, es decir, al tiempo en el que se encuentra disponible. Se pueden distinguir dos tipos principales de disponibilidad:

Disponibilidad en obra o factor de disponibilidad: Se define como el cociente entre el tiempo en que una máquina se encuentra en estado operativo y el tiempo laborable real. En otras palabras, es la relación entre las horas brutas de disponibilidad y las horas que la máquina ha estado presente en la obra. Valores bajos de este factor pueden indicar una mala conservación, reparaciones lentas o falta de repuestos.
Disponibilidad intrínseca: Se define como el cociente entre el tiempo de utilización y el tiempo laborable real, sin tener en cuenta las paradas ajenas a la máquina por tiempo disponible no utilizado (mala organización de la obra, etc.). Estadísticamente, se define como la probabilidad de que una máquina funcione correctamente en un momento determinado o de que no presente averías irreparables en un tiempo máximo.

Las máquinas se clasifican en «principales» (se requiere alta disponibilidad, ya que su fallo paraliza la producción de un conjunto de máquinas) y «secundarias» o «de producción trabajando solas».

¿Cómo se calcula la disponibilidad de un conjunto de máquinas trabajando en cadena y en paralelo?

La disponibilidad de un sistema de máquinas varía significativamente en función de si trabajan en serie o en paralelo.

Máquinas trabajando en cadena (serie): Si n máquinas trabajan en cadena, y el fallo de una paraliza a las demás, la disponibilidad intrínseca del conjunto es el producto de las disponibilidades individuales. Esto significa que la disponibilidad general disminuye rápidamente al aumentar el número de máquinas en serie. Si se admiten acopios intermedios suficientemente grandes, la disponibilidad del equipo sería el mínimo de las disponibilidades individuales, lo que amplía la disponibilidad respecto a no tener acopios.
Máquinas trabajando en paralelo: Si n máquinas iguales trabajan en paralelo y la inoperatividad de una no detiene completamente el proceso (ya que otras pueden seguir trabajando), la probabilidad de que x máquinas se encuentren en disposición sigue una distribución binomial. En este caso, la disponibilidad del conjunto aumenta al tener más unidades en paralelo, ya que el sistema puede continuar operando incluso si algunas máquinas fallan.

En un caso general de máquinas principales en paralelo y auxiliares en paralelo que luego trabajan en serie, la disponibilidad del conjunto se calcula combinando las fórmulas de disponibilidad en serie y en paralelo.

Referencias:

PELLICER, E.; YEPES, V.; TEIXEIRA, J.C.; MOURA, H.P.; CATALÁ, J. (2014). Construction Management. Wiley Blackwell, 316 pp. ISBN: 978-1-118-53957-6.

YEPES, V. (1997). Equipos de movimiento de tierras y compactación. Problemas resueltos. Colección Libro Docente nº 97.439. Ed. Universitat Politècnica de València. 256 pág. Depósito Legal: V-4598-1997. ISBN: 84-7721-551-0.

Curso:

Curso de gestión de costes y producción de la maquinaria empleada en la construcción.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Análisis de deformaciones en cimentaciones profundas en suelo blando

Acaban de publicar nuestro artículo en la revista del primer decil del JCR Journal of Building Enginering. El artículo aborda el desafío técnico y científico que supone analizar las características de deformación en excavaciones profundas en suelos blandos. Estas excavaciones, que están aumentando en escala y complejidad, plantean problemas de estabilidad debido a las propiedades inherentes de los suelos blandos, como su alta compresibilidad, alta sensibilidad, baja permeabilidad y baja resistencia. Además, la interacción entre el agua y el suelo durante la excavación puede causar consolidación por filtración, alteraciones en el campo de tensiones y riesgos significativos para las estructuras circundantes.

Actualmente, los métodos predominantes, como el análisis por elementos finitos y la monitorización experimental, presentan limitaciones a la hora de evaluar la precisión y los efectos espaciales en grandes escalas. Este estudio propone una mejora mediante la modelación tridimensional no lineal que incorpora un modelo de interfaz deslizante. El estudio analiza el proyecto XSS-03-10D, para lo que se utilizan mediciones in situ y simulaciones numéricas con las que estudiar la evolución temporal y espacial de la deformación de los sistemas de soporte y los asentamientos superficiales.

La pregunta principal que guía este trabajo es la siguiente: ¿cómo influye la interacción entre el sistema de soporte y el suelo circundante en la estabilidad y seguridad de las excavaciones profundas en suelos blandos y qué tan efectivas son las herramientas de modelación tridimensional para predecir estos comportamientos?

Este trabajo se enmarca dentro del proyecto de investigación RESILIFE, que dirijo como investigador principal en la Universitat Politècnica de València. Colaboramos con investigadores de la Hunan University of Science and Engineering, de China. A continuación, explicamos brevemente el contenido del artículo que podéis descargar gratuitamente.

Metodología

La metodología empleada en este estudio combina el control exhaustivo en campo con avanzadas simulaciones numéricas para evaluar las características de deformación de las excavaciones profundas. En primer lugar, se realizó un análisis detallado de las condiciones geotécnicas del terreno, incluyendo pruebas de laboratorio y muestreo de suelos en diferentes capas. Gracias a estas pruebas, se identificaron propiedades clave del suelo, como el contenido de humedad, la densidad, la cohesión y el ángulo de fricción interna, que son esenciales para los cálculos posteriores.

Posteriormente, se diseñó un modelo tridimensional no lineal en el programa informático ABAQUS que incorporó las propiedades específicas del suelo y un modelo de interfaz deslizante para simular las interacciones entre el sistema de soporte y el terreno. Este modelo se estructuró en dos capas principales de excavación: la primera, desde la superficie hasta los -7550 m, está compuesta principalmente por relleno y lodo; y la segunda, desde los -7550 m hasta los -10750 m, está formada principalmente por lodo blando.

El modelo numérico se calibró mediante la comparación con datos reales obtenidos de 197 puntos de control distribuidos en el yacimiento. Estos puntos incluían sensores para medir desplazamientos horizontales y verticales, la presión del suelo y las fuerzas axiales en los sistemas de soporte. Además, se integraron sistemas de alerta temprana que permitieron identificar zonas críticas en tiempo real y ajustar las estrategias de soporte en consecuencia.

El análisis se dividió en varias etapas:

Modelación inicial: Se definieron los parámetros básicos del suelo y los límites del modelo. Se realizaron simulaciones preliminares para establecer un marco de referencia.
Simulación del proceso de excavación: Se aplicaron cargas incrementales para replicar el proceso de excavación por capas, teniendo en cuenta los cambios en la presión del suelo y las interacciones dinámicas entre los sistemas de soporte y el terreno.
Validación de resultados: Los resultados del modelo se compararon con los datos de supervisión in situ. Esto incluyó la evaluación de desplazamientos, deformaciones y fuerzas internas, y la realización de ajustes iterativos en el modelo para mejorar la precisión.
Análisis de escenarios críticos: Se exploraron escenarios de fallo potenciales y se identificaron las zonas más vulnerables dentro del sistema de soporte y del terreno circundante.

Esta combinación de monitorización de campo y simulación numérica no solo permitió validar la precisión del modelo tridimensional, sino también obtener una visión integral de los patrones espaciotemporales de deformación.

Aportaciones relevantes

En primer lugar, este trabajo presenta un modelo tridimensional de elementos finitos que combina elasticidad y plasticidad no lineales y que está adaptado para capturar las características específicas de los suelos blandos. Este enfoque supera las limitaciones de los modelos constitutivos tradicionales al integrar datos de campo y parámetros geotécnicos.

En segundo lugar, el estudio identifica los factores clave que afectan a la estabilidad de las excavaciones profundas, como la presión lateral del suelo, los efectos de consolidación y la interacción entre el terreno y la estructura. La comparación entre los datos medidos y los simulados demostró una alta correlación, lo que confirma la precisión del modelo y su aplicabilidad práctica.

Además, el artículo destaca la importancia de realizar un seguimiento continuo y de integrar sistemas de alerta temprana para mitigar riesgos durante la construcción. Este enfoque tiene un impacto directo en la sostenibilidad de los proyectos de infraestructura, ya que reduce el riesgo de fallos estructurales y minimiza el impacto ambiental.

Otra contribución relevante es la identificación de patrones espaciotemporales en la deformación de los sistemas de soporte, lo que permite diseñar estrategias de mitigación más eficaces. Por último, el enfoque metodológico presentado puede adaptarse a otros tipos de proyectos de infraestructura, lo que amplía su aplicabilidad en el campo de la ingeniería civil.

Discusión de resultados

Los resultados del estudio muestran que la deformación de los sistemas de soporte y los asentamientos del suelo presentan patrones espaciotemporales complejos. Durante la excavación por capas, se observó que el sistema de soporte experimentaba un incremento progresivo de las fuerzas axiales, alcanzando valores cercanos a los límites de seguridad en zonas específicas. Estas áreas coinciden con zonas de transición entre diferentes propiedades del suelo y regiones con interacciones más intensas entre el agua y el suelo.

El análisis numérico reveló que el modelo tridimensional es más preciso a la hora de predecir deformaciones y fallos que los métodos tradicionales. Por ejemplo, las simulaciones anticiparon asentamientos y desplazamientos horizontales que coincidieron con los valores observados in situ, lo que proporciona una herramienta fiable para la toma de decisiones durante la construcción.

En cuanto a los desplazamientos horizontales, los datos de control mostraron que los puntos ubicados cerca de áreas de transición de suelos blandos presentaron los mayores valores de deformación. Esto subraya la importancia de diseñar sistemas de soporte que se puedan adaptar dinámicamente a las características específicas del terreno. Por otro lado, los asentamientos superficiales fueron más pronunciados en zonas adyacentes a cuerpos de agua, lo que sugiere que el nivel freático es crucial para la estabilidad de las excavaciones.

Desde el punto de vista del comportamiento estructural, las fuerzas axiales en los soportes interiores aumentaron de forma progresiva durante la excavación, alcanzando valores cercanos a los límites de diseño. Esto demuestra la necesidad de implementar estrategias de refuerzo adicionales en las fases críticas de la construcción. Los resultados también evidenciaron la presencia de efectos de acoplamiento entre el suelo y las estructuras circundantes, un aspecto que podría abordarse en futuros estudios para mejorar la precisión de los modelos predictivos.

Además, se observó que la interacción entre el sistema de soporte y el suelo puede verse significativamente influenciada por factores externos, como las condiciones climáticas y las variaciones en el nivel freático. Estas interacciones tienen implicaciones directas para la estabilidad del sistema, por lo que se deben utilizar estrategias de monitorización adaptativas. Finalmente, los patrones de deformación identificados durante el análisis ponen de manifiesto la importancia de realizar ajustes dinámicos en el diseño y el monitoreo según las condiciones cambiantes en tiempo real.

Futuras líneas de investigación

A partir de los resultados de este estudio, se identifican varias áreas prometedoras para la investigación futura. Una de ellas es mejorar los modelos constitutivos del suelo para tener en cuenta mejor los efectos de la interacción multidimensional entre agua, suelo y estructuras. Esto podría incluir la incorporación de modelos viscoelásticos para simular el comportamiento a largo plazo de los suelos blandos.

Otra línea de interés es el desarrollo de herramientas de simulación que integren datos en tiempo real procedentes de sensores distribuidos en el lugar de la obra. Esto permitiría realizar ajustes instantáneos en las estrategias de construcción, mejorando la seguridad y reduciendo los costes asociados a fallos inesperados.

Además, el estudio destaca la necesidad de investigar la influencia de eventos extremos, como terremotos o lluvias torrenciales, en la estabilidad de excavaciones profundas. Las simulaciones que integran estos escenarios podrían proporcionar datos valiosos para diseñar sistemas de soporte más resilientes.

Finalmente, la investigación sobre métodos sostenibles de construcción en suelos blandos podría beneficiarse de estudios centrados en el uso de materiales de refuerzo ecológicos y en la optimización de diseños que reduzcan la huella de carbono. Estas iniciativas contribuirían al avance de la ingeniería civil hacia un enfoque más respetuoso con el medio ambiente.

Conclusión

El trabajo ofrece un análisis exhaustivo y un marco metodológico innovador para abordar los desafíos de las excavaciones profundas en suelos blandos. Al combinar la supervisión in situ con simulaciones numéricas avanzadas, el estudio asienta las bases para mejorar las prácticas de diseño y construcción.

El uso de modelos tridimensionales no lineales ha demostrado ser una herramienta muy eficaz para predecir comportamientos complejos de deformación y diseñar estrategias de mitigación más efectivas. Esto tiene implicaciones significativas para proyectos de infraestructura en entornos similares, ya que ofrece una guía clara para mejorar la estabilidad y sostenibilidad de estas obras.

En la práctica, los hallazgos refuerzan la importancia del seguimiento continuo y la adaptación dinámica de las estrategias de soporte según las condiciones en tiempo real. Estas prácticas no solo aumentan la seguridad, sino que también reducen los costes y el impacto ambiental asociados a los fallos estructurales.

Finalmente, el estudio sentará las bases para futuras investigaciones que exploren enfoques aún más integrados, sostenibles y resilientes, y permitirá que la ingeniería civil continúe evolucionando frente a los desafíos que presentan los entornos geotécnicos complejos. Además, los resultados invitan a adoptar un enfoque interdisciplinario que combine herramientas tecnológicas avanzadas y principios de sostenibilidad para optimizar tanto los resultados estructurales como el impacto ambiental de las construcciones en suelos blandos.

Referencia:

LI, Y.J.; ZHOU, Z.; ALCALÁ, J.; YEPES, V. (2025). Research on spatial deformation monitoring and numerical coupling of deep foundation pit in soft soil. Journal of Building Engineering, 99:111636. DOI:10.1016/j.jobe.2024.111636

El artículo completo se puede descargar hasta el 14 de febrero de 2025 de forma gratuita en el siguiente enlace: https://authors.elsevier.com/c/1kKko8MyS9AR4g

Qué es una campaña geotécnica y su relevancia en proyectos de ingeniería

Una campaña geotécnica consiste en un conjunto de actividades y estudios técnicos destinados a caracterizar el subsuelo, identificar las propiedades geológicas y geotécnicas relevantes, detectar posibles problemas y garantizar la viabilidad técnica y la seguridad de las obras. Incluye prospecciones (sondeos, calicatas, ensayos), análisis de materiales y condiciones del terreno, que sirven de apoyo a la toma de decisiones en el diseño y construcción. Estas campañas son fundamentales para garantizar la viabilidad técnica, la seguridad y la sostenibilidad de los proyectos, y también para minimizar riesgos y optimizar costes.

En este artículo, profundizaremos en qué consiste una campaña geotécnica, cómo se lleva a cabo y por qué es relevante ejecutarla correctamente en cualquier proyecto de construcción.

El terreno como protagonista en la ingeniería

El terreno es un elemento crucial en cualquier obra. Un conocimiento inadecuado de sus características puede derivar en problemas como asentamientos diferenciales, deslizamientos, licuefacción o incluso colapsos estructurales. Por ello, las campañas geotécnicas son cruciales para diseñar cimentaciones y estructuras adaptadas a las condiciones específicas de cada emplazamiento.

Estas investigaciones se sustentan en tres pilares esenciales:

Experiencia técnica: es indispensable contar con especialistas capaces de identificar las propiedades del terreno, evaluar riesgos y diseñar soluciones personalizadas.
Calidad de ejecución: desde el alcance del estudio hasta la supervisión de campo, cada etapa debe garantizar la precisión de los resultados.
Normativa y seguridad: el cumplimiento de marcos regulatorios, como el Código Técnico de la Edificación (CTE) y la Guía de Cimentaciones en Obras de Carretera, garantiza que las soluciones sean técnicamente adecuadas y cumplan con los estándares establecidos.

Objetivos y beneficios de las campañas geotécnicas

El objetivo principal de una campaña geotécnica es caracterizar el terreno para poder diseñar soluciones constructivas seguras y eficientes. Entre sus ventajas más destacadas se encuentran:

Garantía de seguridad: la identificación de riesgos geotécnicos evita desastres que puedan afectar a personas y estructuras.
Optimización de costes: aunque a menudo se perciben como un coste adicional, estas campañas permiten prevenir gastos futuros en reparaciones o rediseños.
Diseño adaptado: permite elegir los métodos constructivos más adecuados en función de las características del suelo y de las cargas de la estructura.
Mitigación de impactos ambientales y legales: al considerar el entorno y posibles restricciones, se minimizan conflictos y se garantiza la sostenibilidad del proyecto.

Etapas de una campaña geotécnica

1. Recopilación de información previa

Antes de llevar a cabo estudios de campo, es crucial recopilar datos relevantes sobre la zona. Esto incluye:

Planos topográficos: proporcionan una visión detallada del terreno.
Mapas geológicos: permiten identificar características estratigráficas y litológicas.
Historial de uso del terreno: puede revelar posibles riesgos, como rellenos no compactados o estructuras enterradas.
Normativa aplicable: por ejemplo, el Eurocódigo 7 sobre diseño geotécnico.

2. Reconocimientos de campo

Los reconocimientos de campo son el núcleo de una campaña geotécnica. Algunas de las técnicas más comunes son:

Sondeos mecánicos: Perforaciones para extraer muestras y analizar la estratigrafía del terreno.
Ensayos de penetración (SPT, CPT): Evalúan la resistencia del terreno mediante penetraciones controladas.
Calicatas y rozas: Excavaciones superficiales para observar directamente las capas del suelo.
Ensayos geofísicos: Métodos no invasivos, como sísmica de refracción, para obtener una visión global del subsuelo.
Estudios hidrogeológicos: Determinan la posición y características del agua subterránea, que influye en la estabilidad y resistencia del suelo.

Profundidades recomendadas:

Para cimentaciones superficiales, al menos 1,5 veces el ancho proyectado de la cimentación.
Para cimentaciones profundas (pilotes): a una profundidad mínima de 6 metros por debajo de la punta del pilote.

3. Análisis en laboratorio

Las muestras recolectadas se someten a análisis detallados para determinar:

Granulometría y plasticidad: identificación del tipo de suelo y su comportamiento bajo carga.
Resistencia y deformabilidad: ensayos triaxiales y edométricos.
Permeabilidad: evaluación de la capacidad del terreno para drenar agua.

4. Interpretación y diseño geotécnico

Con los datos recopilados, los ingenieros crean modelos y realizan cálculos para encontrar soluciones óptimas para las cimentaciones y las estructuras. Este proceso incluye:

— Selección del modelo de cálculo adecuado.
— Definición de parámetros de seguridad según la normativa.
— Ajustes según observaciones durante la ejecución.

Importancia de una correcta planificación

Construcción de un puente: En un cauce fluvial, por ejemplo, se pueden detectar suelos aluviales inestables, por lo que será necesario diseñar pilotes profundos para evitar asentamientos diferenciales. Por este motivo, se diseñaron pilotes profundos para evitar asentamientos diferenciales.
Proyecto de viviendas: Un caso en el que una zona había sido un vertedero, los estudios geotécnicos identifican rellenos inadecuados. La solución puede ser retirar los rellenos inadecuados y compactar el terreno con materiales adecuados.

Desafíos comunes:

Limitaciones presupuestarias: reducir la intensidad de los estudios puede ocasionar problemas graves durante la construcción.
Condiciones complejas: la heterogeneidad del terreno o la ubicación en zonas sísmicas requieren investigaciones más exhaustivas.
Falta de datos previos: la ausencia de estudios anteriores puede complicar la fase inicial de planificación.

Herramientas y normativas clave

Software especializado: Programas como Plaxis o GeoStudio permiten modelar comportamientos del terreno y simular condiciones críticas.
Normativa aplicable:
- Código Técnico de la Edificación (CTE): Proporciona directrices para reconocer y mitigar riesgos.
- Guía de Cimentaciones en Obras de Carretera: Define protocolos para infraestructuras viales.

Conclusión

Las campañas geotécnicas son mucho más que un paso previo en la construcción: son la base sobre la que se asienta la seguridad, la viabilidad y la sostenibilidad de cualquier proyecto. Al identificar riesgos, garantizar diseños óptimos y cumplir con normativas, estas investigaciones se convierten en una inversión estratégica que previene problemas futuros.

En un entorno cada vez más desafiante para la ingeniería, realizar campañas geotécnicas no solo es una práctica recomendada, sino esencial para asegurar el éxito de cualquier obra.

A continuación dejamos un documento que proporciona recomendaciones técnicas detalladas sobre la campaña geotécnica en proyectos de infraestructura vial para la Dirección General de Carreteras, con el objetivo de establecer criterios uniformes y seguros para la investigación del subsuelo durante las diferentes etapas de desarrollo de un proyecto.

Pincha aquí para descargar

Os dejo también un vídeo al respecto. Espero que os sea de interés.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Maquinaria y procedimientos de construcción: Problemas resueltos

Os presento el libro que he publicado sobre maquinaria y procedimientos de construcción. Se trata de una completa colección de 300 problemas resueltos, abarcando aspectos relacionados con la maquinaria, medios auxiliares y procedimientos de construcción. Su contenido se enfoca en la mecanización de las obras, costos, disponibilidad, fiabilidad y mantenimiento de equipos, estudio del trabajo, producción de maquinaria, sondeos y perforaciones, técnicas de mejora del terreno, control y abatimiento del nivel freático, movimiento de tierras, equipos de dragado, explosivos y voladuras, excavación de túneles, instalaciones de tratamiento de áridos, compactación de suelos, ejecución de firmes, maquinaria auxiliar como bombas, compresores o ventiladores, cables y equipos de elevación, cimentaciones y vaciados, encofrados y cimbras, fabricación y puesta en obra del hormigón, organización y planificación de obras.

Es un libro, por tanto, muy enfocado a los ámbitos de la ingeniería de la construcción, tanto en el ámbito de la edificación, de la minería o de la ingeniería civil. Además, se incluyen 27 nomogramas originales y 19 apéndices para apoyar tanto a estudiantes de ingeniería o arquitectura, como a profesionales que enfrentan desafíos similares en su práctica diaria en obra o proyecto. La colección se complementa con un listado de referencias bibliográficas que respaldan los aspectos teóricos y prácticos abordados en los problemas. Estos problemas son similares a los tratados durante las clases de resolución de casos prácticos en la asignatura de Procedimientos de Construcción del Grado en Ingeniería Civil de la Universitat Politècnica de València (España). Por tanto, el libro resulta adecuado tanto para estudiantes de grado como para cursos de máster relacionados con la ingeniería civil y la edificación.

El libro tiene 562 páginas. Este libro lo podéis conseguir en la propia Universitat Politècnica de València o bien directamente por internet en esta dirección: https://www.lalibreria.upv.es/portalEd/UpvGEStore/products/p_376-7-1

Sobre el autor: Víctor Yepes Piqueras. Doctor Ingeniero de Caminos, Canales y Puertos. Catedrático de Universidad del Departamento de Ingeniería de la Construcción y Proyectos de Ingeniería Civil de la Universitat Politècnica de València. Número 1 de su promoción, ha desarrollado su vida profesional en empresas constructoras, en el sector público y en el ámbito universitario. Ha sido director académico del Máster Universitario en Ingeniería del Hormigón (acreditado con el sello EUR-ACE®), investigador del Instituto de Ciencia y Tecnología del Hormigón (ICITECH) y profesor visitante en la Pontificia Universidad Católica de Chile. Imparte docencia en asignaturas de grado y posgrado relacionadas con procedimientos de construcción y gestión de obras, calidad e innovación, modelos predictivos y optimización en la ingeniería. Sus líneas de investigación actuales se centran en la optimización multiobjetivo, la sostenibilidad y el análisis de ciclo de vida de puentes y estructuras de hormigón.

Referencia:

A continuación os paso las primeras páginas del libro, con el índice, para hacerse una idea del contenido desarrollado.

Pincha aquí para descargar

Orden Circular 4/2023 Procedimiento para la justificación de precios en la Dirección General de Carreteras y base de precios de apoyo

Ha sido para mí un placer participar en la redacción de parte de la Orden Circular 4/2023 sobre el procedimiento para la justificación de precios en la Dirección General de Carreteras y la base de precios de apoyo. El reto ha consistido en presentar explícitamente la metodología subyacente que justifica el precio de las unidades de obra. En este caso, aparece una serie de novedades que creo que son de interés para el sector. Aparece el concepto de unidades de ejecución complejas o atípicas, en las que el empleo de medios singulares las aparta de una construcción estandarizada. También aparece, por vez primera, el concepto de unidades determinantes, que serán las que soporten la mayor parte del importe del presupuesto de una obra. Pues bien, en estos dos casos, se obliga a una justificación expresa y detallada de las unidades de obra. Solo para los casos del resto de unidades, se aporta la base de precios como un apoyo para la justificación de los precios, sin que tampoco deba considerarse como un objetivo de precio concreto a utilizar.

Un aspecto también importante ha sido dejar claros los conceptos que se manejaban, con el paso del tiempo, de forma inadecuada. Un ejemplo es el Cuadro de Precios N.º 2, donde se prohíbe expresamente su desglose en las siguientes categorías genéricas: mano de obra, maquinaria, resto de obra, materiales y costes indirectos.

El documento presenta, también, una serie de anexos que complementan el procedimiento, en las que he participado especialmente en el Anexo 4:

Anexo 1: Convenios colectivos del sector de la construcción por provincias.
Anexo 2: Listado de precios básicos de los principales materiales.
Anexo 3: Justificación de los precios de las unidades de ejecución de la obra. Ejemplos.
Anexo 4: Método simplificado de cálculo de la producción de una máquina.
Anexo 5: Base de precios de apoyo de la D.G.C.

La redacción de este documento ha sido fruto del esfuerzo de un grupo de trabajo de la Subdirección General de Proyectos y Obras de la Dirección General de Carreteras del Ministerio de Transportes, Movilidad y Agenda Urbana. Mi especial agradecimiento por la confianza depositada en mi persona por parte de su titular, D. Fernando Pedrazo Majárrez. También se ha contado con el soporte del encargo a INECO, con la participación expresa de D. José Manuel Sáez Serrano, Dña. María del Consuelo Martín Galán y D. Javier Fernández Pedroche, entre otro personal. Igualmente, se ha contado con la participación en el grupo de trabajo del Comité de Construcción y de la Comisión de Maquinaria de SEOPAN. Mi agradecimiento personal a todos ellos, pues su visión y sus aportes son de gran interés para el documento.

Por último, mi recomendación es que se lea con detenimiento el documento, pues existen modificaciones que deberían tenerse en cuenta a partir de este momento. Además, tal y como se ha establecido en estas reuniones, el objetivo es mejorar paulatinamente el documento en futuras ediciones. Por mi parte, este documento lo voy a poner a circular entre mis estudiantes de la Escuela de Ingeniería de Caminos, Canales y Puertos para su aplicación inmediata en TFGs y TFMs.

Además, para los que estéis interesados, un desarrollo completo sobre los temas de costes y producción de los equipos los podéis seguir en el siguiente curso: https://ingeoexpert.com/cursos/curso-de-gestion-de-costes-y-produccion-de-la-maquinaria-empleada-en-la-construccion/

Os dejo, para su descarga, el documento completo. Espero que les sea de interés.

Pincha aquí para descargar

Nomogramas para su empleo en trabajos de movimiento de tierras

Este artículo presenta cinco nomogramas originales que pueden ser utilizados en proyectos de movimientos de tierra. El primero de ellos calcula el peso específico aparente de un suelo, mientras que el segundo nomograma facilita el valor de la piedra en el diseño de voladuras según la metodología de Ash. Los dos siguientes se aplican para determinar la capacidad de la hoja empujadora de un buldócer, y finalmente, el último nomograma ayuda a calcular el rendimiento de escarificado de un buldócer.

Estos nomogramas demuestran también las capacidades de los programas de código abierto, PyNomo y Nomogen, para generar nomogramas adaptados a las necesidades de cálculo de cualquier proyectista. Este proyecto es el resultado de una colaboración internacional entre profesores de Finlandia, Canadá y Australia, y su artículo ha sido publicado en la revista inGEOpress en mayo de 2023.

En este trabajo se proporcionan cinco nomogramas originales generados con el programa Pynomo (http://lefakkomies.github.io/pynomo-doc/introduction/introduction.html), muy útiles para su empleo en trabajos de obra civil, movimiento de tierras y/o minería, así como en ámbito docente. Los ejemplos resueltos por cada uno de los nomogramas también demuestran que los valores obtenidos se obtienen con una precisión adecuada a los requerimientos que se exigen en ingeniería de proyectos, haciéndolos útiles cuando no se tiene acceso a ordenadores o a calculadoras programables y, especialmente, en el manejo de ecuaciones cuyo empleo sea repetitivo.

Referencia:

MARTÍNEZ-PAGÁN, P.; YEPES, V.; ROSCHIER, L.; BOULET, D.; BLIGHT, T. (2023). Nomogramas para su empleo en trabajos de movimiento de tierras. Canteras y explotaciones, 657(3):44-48.

Os paso a continuación el artículo entero por si os resulta de interés.

Pincha aquí para descargar

Curso:

Curso de gestión de costes y producción de la maquinaria empleada en la construcción.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Deflexión de una capa compactada

A continuación os dejo una sencilla demostración del asiento que tiene una capa que se ha compactado en función de su espesor inicial y de los pesos específicos anterior y posterior a la compactación. Se trata de una forma indirecta de controlar si se ha alcanzado el grado de compactación deseado. También permite tener una idea de cuánto va a descender la capa una vez compactada.

Si quieres conocer más sobre los aspectos de la compactación, te recomiendo que revises las referencias que dejo al final del post y también este curso en línea sobre “Compactación superficial y profunda de suelos en obras de ingeniería civil y edificación”. Toda la información la puedes encontrar en esta página: https://ingeoexpert.com/cursos/curso-de-compactacion-superficial-y-profunda-de-suelos-en-obras-de-ingenieria-civil-y-edificacion/

Para aquellos nostálgicos de los nomogramas, os dejo uno preparado específicamente para este caso. Espero que os guste.

Pincha aquí para descargar

Referencias:

YEPES, V. (1997). Equipos de movimiento de tierras y compactación. Problemas resueltos. Colección Libro Docente n.º 97.439. Ed. Universitat Politècnica de València. 253 pág. ISBN: 84-7721-551-0.

Cursos:

Curso de compactación superficial y profunda de suelos en obras de ingeniería civil y edificación.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.