Categoría: canalizaciones

Rehabilitación de tuberías mediante manga continua CIPP

1. Introducción: concepto y finalidad de la rehabilitación CIPP

Las redes de tuberías existentes están sometidas a procesos de deterioro que pueden afectar tanto su capacidad funcional como su comportamiento estructural. Cuando una conducción alcanza un estado que requiere intervención, la sustitución mediante la apertura de zanja no es necesariamente la única alternativa. Las tecnologías sin zanja permiten construir, reemplazar o reparar conducciones, reduciendo la excavación y, con ello, la afectación a la superficie. Entre las técnicas de renovación sin zanja se encuentran el pipe bursting, el entubado simple, el entubado ajustado y la manga continua (CIPP).

CIPP corresponde a Cured-in-Place Pipe, una técnica que permite crear una nueva tubería dentro de la conducción existente. El procedimiento parte de una manga flexible, constituida por una matriz fibrosa impregnada con una resina termoendurecible. La manga se introduce en la tubería que se pretende rehabilitar y, posteriormente, se somete a un proceso de curado. La polimerización de la resina transforma el conjunto en un tubo estructural continuo adaptado al interior de la conducción existente.

La característica que define al sistema es, por tanto, que la nueva conducción se fabrica in situ. No se introduce un tubo rígido convencional, sino un material flexible que adquiere sus propiedades finales durante el proceso de instalación y curado. Esto permite rehabilitar conducciones manteniendo una ocupación superficial reducida y evitando la excavación de una zanja longitudinal.

La elección de CIPP no debe entenderse únicamente como una decisión relacionada con el método constructivo. La rehabilitación exige estudiar previamente el estado de la conducción, sus condiciones geométricas, las cargas que actúan sobre ella, el terreno y las condiciones hidráulicas. La rehabilitación debe planificarse, pasando de una respuesta basada exclusivamente en la reparación de averías a una gestión preventiva de la infraestructura.

Las ventajas asociadas a la técnica abarcan diferentes dimensiones. Desde el punto de vista urbano, la ausencia de excavación continua reduce la ocupación de la vía pública y disminuye las interferencias con el tráfico. Desde el punto de vista funcional, el tubo continuo mejora la estanqueidad y elimina las juntas propias de la conducción original, reduciendo problemas relacionados con infiltraciones, raíces y uniones deterioradas. También se indica una mejora hidráulica asociada al coeficiente de rugosidad y una elevada resistencia frente a la abrasión y diferentes tipos de efluentes.

2. Estudio de la conducción y diseño de la rehabilitación

Una rehabilitación CIPP comienza antes de introducir la manga. El conocimiento preciso de la conducción existente condiciona todas las fases posteriores. Por ello, el procedimiento contempla una inspección inicial completa del colector, acompañada de su limpieza, y un reconocimiento de la obra realizado por personal cualificado. Se realizan mediciones in situ del tramo que debe rehabilitarse, se identifican los pozos de registro y se determina la profundidad del colector respecto de la solera. También se estudian los accesos y las necesidades de by-pass.

La inspección mediante CCTV constituye una herramienta relevante en esta fase. Su combinación con el reconocimiento de la obra y el diseño permite contar con una visión integral del tramo. El objetivo no consiste únicamente en conocer la longitud y el diámetro de la tubería. Es necesario identificar las condiciones que pueden afectar la instalación de la manga, como resaltos, acometidas, obstáculos o características geométricas particulares.

El diseño de la manga se realiza de forma individual para cada instalación. Uno de los parámetros que debe determinarse es el espesor necesario del tubo curado. El cálculo considera las condiciones particulares de la conducción y los siguientes factores: profundidad, tipo de terreno, nivel freático, cargas de tráfico y cargas vivas. La situación estructural del colector también incide en el diseño, y en la documentación se distinguen diferentes estados de deterioro.

El diseño condiciona, además, la planificación de la ejecución. La pendiente, la longitud y los diámetros de los tramos, los resaltos, las acometidas, la necesidad de by-pass, el transporte y las características de la resina inciden en la determinación del número de instalaciones. Por ello, una conducción de gran longitud no necesariamente debe rehabilitarse mediante una única manga. El tramo puede dividirse en varias instalaciones, seleccionando los puntos de acceso y las longitudes de cada manga según las condiciones reales de la obra.

La documentación recoge diversas normas de referencia para el diseño, el control y la instalación de sistemas CIPP. Entre ellas figuran la UNE-EN ISO 11296-4:2018 para redes de alcantarillado y saneamiento sin presión y la UNE-EN ISO 11297-4:2018 para redes con presión. También se citan la ISO/DIS 11298-4:2018, la ASTM F1216-16 y la ASTM F2019-17. En España, la UNE 53929 establece criterios relativos al diseño, cálculo e instalación de conducciones de abastecimiento y de alcantarillado rehabilitadas mediante tubos continuos curados in situ.

La normativa, por tanto, no aparece como una fase independiente del proceso, sino como una referencia que condiciona el diseño y los controles posteriores. La geometría de la conducción, las condiciones del terreno, las solicitaciones y el estado existente deben traducirse en una solución de manga con características definidas antes de comenzar la instalación.

 

3. Preparación de la conducción y fabricación de la manga

Una vez definida la solución, la conducción debe prepararse para recibir la manga. La limpieza constituye una operación previa indispensable, ya que la superficie interior debe quedar libre de materiales que puedan interferir con la instalación o con la adaptación de la manga a la conducción existente. El procedimiento contempla el uso de equipos de succión-impulsión y la realización de trabajos específicos para eliminar obstáculos.

Entre las actuaciones preparatorias se encuentran el fresado de obstáculos, las incrustaciones, las sedimentaciones y las acometidas penetrantes. También se localizan y se miden las acometidas existentes. Esta información será necesaria posteriormente para restablecer las conexiones una vez completado el curado. La preparación no se limita, por tanto, a limpiar la tubería: busca dejarla en condiciones adecuadas para que la manga pueda introducirse, posicionarse y curarse correctamente.

La manga se fabrica de acuerdo con las especificaciones definidas durante el diseño. Se distinguen fundamentalmente dos familias de textiles: el fieltro y la fibra de vidrio. La elección está relacionada con la solución prevista y con el procedimiento de curado que se utilizará posteriormente. También pueden emplearse diferentes tipos de resina en función del efluente que circulará por la conducción rehabilitada.

La impregnación con resina puede realizarse en las instalaciones de fabricación o en la propia obra. El resultado es una manga flexible, lista para su instalación en la conducción. En esta fase resulta especialmente relevante la correspondencia entre las especificaciones de fabricación y el diseño realizado para el tramo concreto. El material de la manga, su espesor y la resina deben cumplir con las condiciones previstas para la conducción rehabilitada.

La planificación previa adquiere especial relevancia cuando existen diferentes instalaciones en una misma obra. La longitud de cada manga, los puntos de acceso, las acometidas, el sistema de by-pass, los medios de transporte y las condiciones de trabajo deben coordinarse antes de iniciar la instalación. El objetivo es limitar los riesgos y asegurar que las operaciones de introducción y curado se desarrollen según el diseño previsto.

4. Instalación y curado de la manga

La fase de instalación constituye el núcleo del proceso CIPP. Comprende dos operaciones relacionadas: la introducción de la manga en la conducción existente y la polimerización de la resina. Existen tres posibilidades de inserción: mediante columna de agua, mediante aire a presión o mediante tiro. Para el curado se contemplan el calentamiento del agua, el vapor de agua y la luz ultravioleta.

4.1. Inversión mediante columna de agua y calentamiento con agua

En este procedimiento, la manga se introduce mediante una columna de agua y, posteriormente, se utiliza agua sobrecalentada para proporcionar las condiciones necesarias para el curado de la resina. El sistema presenta una elevada versatilidad y puede emplearse en diferentes secciones, diámetros y longitudes. El material se relaciona especialmente con conducciones que presentan problemas de infiltración.

La versatilidad de este procedimiento permite abordar configuraciones geométricas diversas. Los casos incluidos en la documentación muestran su aplicación tanto en conducciones circulares como en secciones ovoidales, así como en rehabilitaciones a gran escala. En una intervención sobre una conducción de sección ovoide de 2100 × 1400 mm, por ejemplo, se realizaron dos instalaciones desde un único pozo de ataque y fue necesario disponer de un by-pass mediante un tanque de tormentas.

4.2. Inversión mediante aire y curado con vapor

Otra configuración utiliza aire a presión para invertir la manga y vapor de agua para el curado. ES especialmente adecuada para longitudes y diámetros medios, habituales en las redes urbanas. El tiempo de ejecución puede ser inferior a una jornada de trabajo, lo que contribuye a reducir las molestias para el entorno. Esta modalidad permite utilizar mangas de fieltro o de fibra de vidrio.

La aplicación de esta tecnología se observa en ejemplos de rehabilitación de redes de saneamiento. En dichos casos se emplean mangas de fieltro o de fibra, con resina de poliéster en la mayoría de las aplicaciones, y el diseño es estructural. La profundidad de las conducciones recogidas en los ejemplos oscila entre 1,5 y 8,5 m.

4.3. Inserción por tiro y fotopolimerización

La tercera alternativa consiste en introducir la manga mediante tiro y curarla con luz ultravioleta. El procedimiento está orientado a diámetros medios y longitudes cortas y presenta tiempos de instalación reducidos. Una particularidad del sistema es que permite visualizar el curado durante la instalación.

En esta modalidad se utilizan mangas de fibra de vidrio. El menor espesor de este material facilita el curado mediante el haz de radiación ultravioleta. Un ejemplo de rehabilitación de 2000 m en conducciones de DN200 a DN500, con profundidades entre 1,5 y 3 m, en el que se empleó una manga de fibra y resina de poliéster mediante inserción por tiro y fotopolimerización.

La existencia de estas tres modalidades demuestra que CIPP no constituye un procedimiento de ejecución único. La solución debe seleccionarse según las características de la conducción, la longitud y el diámetro del tramo, el material de la manga, la resina y las condiciones particulares de la obra. La fase de diseño y planificación permite determinar qué sistema es compatible con cada actuación.

5. Recepción, prestaciones y aplicación a grandes diámetros

El proceso no termina con el curado. La recepción permite comprobar que la rehabilitación se ha ejecutado correctamente y que la nueva conducción cumple las condiciones previstas. Una de las operaciones consiste en reabrir las acometidas mediante un robot fresador. Posteriormente, se realiza una inspección mediante CCTV para verificar el estado del interior de la manga instalada. También se realizan pruebas de estanqueidad y, cuando corresponde, de presión.

El control incluye ensayos mecánicos conforme a la norma UNE-EN ISO 11296-4:2018, realizados por un laboratorio independiente. De este modo, la recepción combina inspección visual, comprobaciones hidráulicas y controles mecánicos. La finalidad es verificar tanto la continuidad y la funcionalidad del tubo como las propiedades asociadas al diseño especificado para la rehabilitación.

Los casos incluidos en la documentación permiten relacionar las diferentes fases del procedimiento con situaciones reales de rehabilitación. En una conducción de abastecimiento de 670 m de longitud, con una profundidad de 5 m y una presión de trabajo de 9 bar, se emplearon un textil de fieltro de polietileno y fibra de vidrio, una resina apta para conducciones de agua potable y un sistema de columna de agua. La conducción presentaba un deterioro generalizado y numerosas averías en un tramo urbano con edificaciones próximas a la servidumbre del colector.

En otro caso se rehabilitaron 600 m de conducción con un diámetro de 1000 mm y una profundidad de 4 m. El problema existente era la filtración en las juntas, y la solución consistió en un diseño estructural mediante manga de fieltro y resina de poliéster, instalada mediante columna de agua.

Los grandes diámetros incrementan las exigencias de planificación. En una conducción circular de 1600 mm de diámetro y 317 m de longitud, la problemática se centraba en las filtraciones, los vertidos al río y las dificultades de acceso. La solución contempló un diseño conforme a la UNE 53929, con un espesor de 28 mm y dos instalaciones desde un único pozo de ataque. Previamente se había dispuesto un by-pass para permitir las labores de limpieza e inspección del colector.

Otro caso corresponde a una conducción de sección circular de 1200 mm y 530 m de longitud, afectada por ovalización, filtraciones, ubicación desfavorable y por el fin de su vida útil. El diseño conforme a la UNE 53929 condujo a espesores de 28-30 mm y a seis instalaciones desde tres puntos de ataque. Al tratarse de un colector de aguas pluviales, no fue necesario instalar un by-pass. La longitud total se rehabilitó en cinco semanas, considerando aproximadamente una semana por cada manga instalada por completo.

Estos ejemplos permiten entender una característica relevante del CIPP: la solución no se define únicamente por el diámetro de la tubería. El estado de deterioro, la geometría, la longitud, la profundidad, el régimen hidráulico, los accesos y las condiciones del entorno intervienen simultáneamente. Por ello, la rehabilitación requiere una planificación específica para cada tramo.

6. Conclusiones: de la reparación puntual a la gestión planificada de la red

La manga continua CIPP permite rehabilitar una conducción existente, generando en su interior un tubo continuo mediante la instalación y el curado de una manga impregnada con resina. El proceso integra inspección, diseño, preparación, fabricación, instalación y recepción. Cada fase condiciona la siguiente, de modo que la calidad de la solución final depende de que el conjunto del procedimiento se haya definido y ejecutado de forma coherente.

Las prestaciones incluyen estanqueidad, características estructurales, mejora hidráulica, rapidez de instalación y una solución duradera. La técnica puede emplearse tanto en redes sin presión como en redes presurizadas, siempre que el diseño se adapte a las condiciones de servicio. La ausencia de juntas en el tubo rehabilitado permite abordar problemas de infiltración y otros defectos asociados a las uniones de la conducción existente.

La reducción de la excavación también modifica el impacto de la obra. Existe una menor ocupación de la vía pública, menos molestias para el entorno y una huella de carbono inferior a la de los sistemas tradicionales. La documentación cifra esta reducción, como mínimo, en un 75 %. También se señala una menor necesidad de mantenimiento y una mayor eficiencia económica de la solución.

Sin embargo, la principal enseñanza técnica del procedimiento no se limita a las características de la manga. La rehabilitación CIPP debe integrarse en una estrategia de gestión de activos. Se plantea un cambio de un modelo reactivo, basado en actuar cuando se produce una avería, a un modelo preventivo, basado en inspeccionar, diagnosticar, priorizar, rehabilitar, verificar y volver a evaluar.

Para el ingeniero, CIPP debe entenderse como una solución técnica que comienza mucho antes de la instalación física de la manga. La decisión sobre qué tramo rehabilitar, cómo diseñarlo, qué espesor requiere, qué material utilizar, qué procedimiento de inserción y curado seleccionar, cómo organizar los accesos y cómo verificar el resultado forma parte de un único proceso de ingeniería. La rehabilitación deja de ser una actuación aislada sobre una tubería deteriorada y pasa a integrarse en la gestión planificada del ciclo de vida de la infraestructura.

En esta conversación puedes escuchar las ideas más interesantes sobre este sistema.

Os dejo algunos vídeos sobre esta técnica.

Referencia:

Patón Sanz, R. M. (2026). Rehabilitación de tuberías con manga continua: Sistema CIPP. Material docente del XII Curso de Postgrado Especialista en Tecnologías Sin Zanja.

Licencia de Creative Commons
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Rehabilitación de conducciones mediante Spray Lining

1. Introducción

El Spray Lining es una técnica de rehabilitación de conducciones existentes que permite recuperar las condiciones de servicio de una tubería mediante la formación de un nuevo revestimiento en su interior. Se integra en las tecnologías sin zanja y está especialmente orientado a redes de abastecimiento y a otras conducciones sometidas a presión. Su desarrollo comenzó a finales de la década de 1970 y principios de la década de 1980, y la evolución de los procedimientos ha permitido mejorar aspectos relacionados con la facilidad de aplicación, la durabilidad y la capacidad estructural del revestimiento. El material también se utiliza en conducciones destinadas al transporte de agua potable.

La finalidad de la intervención puede estar relacionada con distintos procesos de deterioro de la conducción original. Entre ellos se encuentran las grietas, las fugas, la corrosión y la presencia de poros. La rehabilitación mediante revestimiento permite intervenir en el interior de la conducción, manteniendo la tubería existente como parte del sistema rehabilitado. Por ello, antes de seleccionar y dimensionar la solución, es necesario conocer las condiciones reales de la tubería y determinar qué función estructural continuará desempeñando tras la intervención.

El procedimiento no consiste únicamente en proyectar un material sobre la pared interior. La intervención comprende una sucesión de operaciones que comienza con la apertura de accesos y el aislamiento de la conducción, continúa con su limpieza e inspección, prosigue con la aplicación controlada del revestimiento y termina con la inspección, desinfección, reconexión y puesta en servicio. Cada una de estas fases condiciona a la siguiente, por lo que la calidad final depende tanto del revestimiento como de la correcta preparación y del control de la conducción existente.

2. Clasificación de las soluciones y evaluación del estado de la conducción

La clasificación de una solución de rehabilitación debe relacionarse con la capacidad resistente que aporta el nuevo sistema y con la función que conserva la tubería original. La documentación distingue entre dos conceptos fundamentales: las soluciones independientes o estructurales y las soluciones interactivas o semiestructurales. En una solución independiente o estructural, la manga es capaz de resistir por sí sola, sin fallar, todas las cargas internas aplicables durante su vida de diseño. En una solución interactiva o semiestructural, el revestimiento no posee por sí mismo la capacidad de soportar todas las cargas previstas y requiere la colaboración de la tubería original.

Esta distinción guarda una relación directa con el estado de deterioro de la conducción. La evaluación previa debe considerar el material y la antigüedad de la tubería, su estado físico, las incrustaciones, los orificios, el espesor de la pared, las juntas y las grietas. También deben analizarse la ovalidad, las cargas externas y el nivel freático. A ello se añaden las condiciones del terreno, incluyendo el peso, el tipo y la granulometría del relleno, así como la presión interna de trabajo. La finalidad es determinar qué solicitaciones inciden en la conducción rehabilitada y qué capacidad resistente puede seguir aportando la tubería original.

Se puede diferenciar entre deterioro parcial y deterioro total. En el deterioro parcial, la tubería original conserva capacidad suficiente para soportar el terreno y las sobrecargas durante la vida útil prevista de la tubería rehabilitada. En el deterioro total, la conducción original ha perdido su resistencia estructural y no puede soportar las acciones externas del terreno y las sobrecargas, o se prevé que alcance esa condición durante la vida prevista de la rehabilitación. Esta clasificación permite determinar el papel que puede desempeñar la tubería existente en el sistema rehabilitado.

La documentación relaciona estas categorías con distintos criterios normativos. Para el diseño de sistemas a presión, se indica el uso de la norma ASTM F1216-16, que diferencia entre tubería parcialmente deteriorada y totalmente deteriorada. También se citan las normas alemanas DWA-A 143-2:2015 y francesa ASTEE 3R2014, que consideran tres estados de la tubería. Los estados I y II de estas últimas corresponden al concepto de «parcialmente deteriorada» según ASTM, mientras que el estado III equivale al concepto de «totalmente deteriorada».

Para una conducción a presión parcialmente deteriorada, el diseño debe evaluar las cargas hidrostáticas externas y las cargas asociadas a la presión interna que actúan en expansión a través de los orificios. Entre los factores que intervienen se encuentran el nivel freático, el módulo de elasticidad a largo plazo del revestimiento, la relación entre el tamaño del orificio y el diámetro de la conducción, así como las resistencias a la flexión y a la tracción a largo plazo. El comportamiento del sistema se analiza, por tanto, teniendo en cuenta la interacción entre el revestimiento y la tubería existente.

La situación cambia cuando la conducción se considera totalmente deteriorada. En este caso, el diseño debe contemplar todas las cargas externas, incluidas las producidas por el nivel freático, el peso del terreno y las sobrecargas del suelo, como las asociadas al tráfico o a estructuras situadas sobre la conducción. También deben considerarse todas las cargas derivadas de la presión interna. El revestimiento debe dimensionarse considerando este escenario de solicitación, dado que la tubería original ya no aporta la resistencia estructural necesaria.

El sistema Spray Lining se clasifica como un sistema semiestructural de clase III. Esto significa que su concepción corresponde a una solución en la que la tubería existente continúa formando parte del comportamiento resistente del conjunto. Se aplica en redes a presión, incluidas las de agua potable, los sistemas de bombeo y las redes industriales. Asimismo, el sistema puede aumentar la capacidad de la tubería y resolver diversos problemas habituales en las redes de agua potable.

3. Preparación, acceso, aislamiento y limpieza de la conducción

La ejecución del Spray Lining comienza con la creación de los accesos necesarios para intervenir en la tubería existente. El procedimiento contempla la excavación de accesos y el corte de la conducción original. La ubicación del acceso se selecciona en un punto que facilite la intervención, pudiendo situarse en elementos como válvulas, tes, hidrantes o codos. La cata puede tener dimensiones de referencia de 2,0 × 1,0 m, con una profundidad acorde con la posición de la tubería. También indica que los codos con un ángulo superior a 22,5° deben retirarse.

La apertura de estos accesos permite disponer de los puntos necesarios para introducir los equipos y realizar las operaciones posteriores durante la conducción. Su posición está directamente relacionada con la geometría de la tubería y la configuración de los elementos existentes. Por ello, la fase inicial no debe entenderse como una actuación independiente, sino como la preparación física que permite ejecutar las operaciones de aislamiento, limpieza, inspección y revestimiento.

Una vez disponibles los accesos, la conducción debe quedar aislada antes de iniciar las operaciones interiores. El aislamiento permite trabajar en la tubería en las condiciones requeridas por el procedimiento y preparar su superficie para la aplicación del revestimiento. La secuencia del sistema sitúa esta operación inmediatamente antes de la limpieza, seguida de una inspección de la conducción.

La limpieza tiene como finalidad eliminar las incrustaciones acumuladas en el interior de la tubería. La documentación contempla tres posibilidades principales: equipos de agua a alta presión, sistemas mecánicos y sistemas combinados. En los sistemas mecánicos se identifica el uso de equipos de tipo rack-feed. La elección del sistema de limpieza forma parte de la preparación necesaria para lograr las condiciones adecuadas de la superficie interior antes de aplicar el revestimiento.

La limpieza adquiere especial relevancia porque el revestimiento se aplica directamente sobre la superficie interior existente. Por ello, las incrustaciones y otros elementos presentes en la pared deben eliminarse antes de continuar con la intervención. Tras esta operación se realiza una inspección de la tubería, incluida en la secuencia del procedimiento, que permite comprobar las condiciones de partida antes de ejecutar el revestimiento.

4. Aplicación del revestimiento mediante Spray Lining

Con la tubería preparada se inicia propiamente la operación de revestimiento interior. El procedimiento comienza con el posicionamiento del equipo y la introducción de una manguera en el interior de la conducción hasta alcanzar la cata de salida. Una vez situada la manguera, se realiza el acoplamiento del mezclador y del cabezal rociador, que constituye el elemento encargado de proyectar el material sobre la superficie interior de la tubería.

El cabezal se desplaza posteriormente a lo largo del interior de la conducción hacia la cata de entrada. Este desplazamiento se realiza mediante una torre de revestimiento que permite controlar la velocidad de avance. Mientras el cabezal se desplaza, se proyecta poliurea sobre la superficie interior. El control de la velocidad forma parte del procedimiento, ya que el revestimiento debe alcanzar el espesor de diseño previsto para la solución.

Existen distintos valores de referencia de espesores de diseño para diferentes diámetros y clases. Para la clase I, el espesor indicado es de 1,2 mm para los diámetros comprendidos entre 100 y 610 mm incluidos en la tabla. Para la clase IV, el espesor aumenta con el diámetro: 3,5 mm para diámetros de 100, 150, 200 y 250 mm; 4,5 mm para 300 mm; 5,0 mm para 350 mm; 5,75 mm para 400 mm; 7,25 mm para 500 mm; 8,0 mm para 560 mm y 8,5 mm para 610 mm.

Estos valores muestran que el espesor del revestimiento forma parte de la concepción técnica del sistema y no constituye una magnitud independiente ni del diámetro ni de la clase considerada. El procedimiento de proyección debe permitir alcanzar el espesor previsto de forma controlada, por lo que el movimiento del cabezal se realiza a una velocidad regulada.

Una vez finalizada la proyección, se inicia el curado de la poliurea. A una temperatura de secado y curado de 20 °C, el tiempo mínimo indicado para alcanzar el gel es de un minuto, y el correspondiente a la formación de la película, de tres minutos. A los diez minutos, se contempla la posibilidad de realizar la inspección mediante CCTV, mientras que el curado total se sitúa en sesenta minutos y el tiempo de servicio, en noventa minutos.

Los tiempos de curado permiten organizar las operaciones posteriores. No debe confundirse el momento en que se dispone de una película formada con el curado total con el tiempo establecido para la puesta en servicio. Se deben diferenciar expresamente estos estados y fijar noventa minutos como tiempo de servicio bajo las condiciones de temperatura indicadas. El resumen del sistema confirma que los tramos revestidos pueden ponerse en servicio una vez transcurridos 90 minutos.

5. Control del revestimiento, desinfección y puesta en servicio

La inspección posterior constituye una fase de control de calidad del revestimiento ejecutado. Se recomienda realizar una inspección mediante CCTV una vez transcurridos 10 minutos desde el curado inicial de la resina. El objetivo es comprobar el estado y la calidad del revestimiento y detectar posibles problemas. Una ventaja de realizar esta comprobación en la fase temprana indicada por el procedimiento es que los defectos identificados pueden rectificarse en ese momento.

La inspección debe entenderse como la comprobación del resultado de las operaciones anteriores. Hasta este punto se han producido varias transformaciones sucesivas: se ha aislado la conducción, se han eliminado las incrustaciones, se ha inspeccionado la tubería original, se ha proyectado el revestimiento y se ha iniciado su curado. La inspección mediante CCTV permite comprobar visualmente el estado final del revestimiento antes de aceptar la intervención y avanzar hacia las operaciones de puesta en servicio.

Una vez que el revestimiento ha sido aceptado, comienza la fase final del procedimiento. La conducción se desinfecta y se lava antes de su reconexión. Después de completar estas operaciones, la tubería puede ser reconectada y puesta nuevamente en servicio. El procedimiento, por tanto, no termina con la proyección ni con el curado del revestimiento, sino con la recuperación de las condiciones necesarias para que la conducción vuelva a formar parte de la red.

La secuencia completa puede resumirse en una cadena de ocho operaciones: apertura de accesos, aislamiento de la tubería, limpieza, inspección de la tubería, revestimiento, inspección posterior, desinfección y puesta en servicio. Esta secuencia ordena el proceso desde la preparación física para la conducción hasta la recuperación funcional. Cada etapa tiene una finalidad concreta y prepara las condiciones para la siguiente.

6. Conclusiones

El Spray Lining es una técnica de rehabilitación sin zanja que permite intervenir en conducciones existentes mediante la formación de un revestimiento interior. Su aplicación exige conocer previamente el estado de la tubería, sus condiciones geométricas y las solicitaciones que soporta. La clasificación entre soluciones estructurales y semiestructurales permite determinar si el nuevo sistema debe asumir por sí mismo las cargas consideradas o si requiere la colaboración de la conducción existente como elemento resistente.

La clasificación del estado de la tubería como parcialmente o totalmente deteriorada condiciona el análisis de las acciones que deberá soportar el sistema rehabilitado. En el primer caso, se considera que la conducción original mantiene la capacidad de soportar el terreno y las sobrecargas; en el segundo, esa capacidad estructural se ha perdido o se prevé que se pierda durante la vida útil prevista. Para las conducciones a presión, el análisis incorpora tanto las acciones externas como las derivadas de la presión interna, con distintos factores de diseño según el estado de deterioro.

La ejecución de una solución semiestructural de clase III requiere una preparación cuidadosa de la conducción, que comienza con los accesos y el aislamiento y continúa con la limpieza para eliminar las incrustaciones. Posteriormente se introduce el equipo de proyección, se desplaza el cabezal a velocidad controlada y se aplica la poliurea sobre la superficie interior hasta alcanzar el espesor previsto.

El control posterior completa el proceso. La inspección mediante CCTV permite comprobar el revestimiento y detectar posibles problemas, que pueden rectificarse en la fase indicada por el procedimiento. Una vez aceptado el resultado, la conducción se desinfecta, se lava y se reconecta. Bajo las condiciones de curado indicadas en la documentación, el tiempo de servicio establecido es de 90 minutos. De este modo, la técnica combina la rehabilitación del interior de la conducción con una secuencia controlada de preparación, aplicación, curado, inspección y recuperación del servicio.

Os dejo algunos vídeos que explican esta técnica.

Referencia:

Álvarez de Miguel, A. (2026). Rehabilitación de conducciones mediante Spray Lining [Material docente del módulo M3-7, XI edición del Curso Especialista en Tecnologías sin Zanja].

Licencia de Creative Commons
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

La ciudad que se repara sin abrirse en canal

Las tecnologías sin zanja permiten renovar tuberías y colectores reduciendo excavaciones, residuos, tráfico y molestias. La experiencia de Murcia muestra cómo estas técnicas pueden convertirse en una alternativa para afrontar el envejecimiento de las redes de agua, que requieren una mayor inversión.

Bajo el asfalto de las ciudades existe una infraestructura que casi nunca vemos y que, sin embargo, sostiene una parte esencial de nuestra vida cotidiana. Kilómetros de tuberías llevan agua potable hasta los edificios y transportan las aguas residuales hacia las instalaciones donde serán tratadas. Muchas de esas redes fueron construidas hace décadas y ahora necesitan ser renovadas. El problema es cómo hacerlo sin convertir las calles en grandes obras durante semanas o meses.

Verdú y Gázquez (2025), de Aguas de Murcia, sitúan el envejecimiento de estas infraestructuras entre los principales retos de la gestión del agua. Una parte importante de las redes españolas se instaló entre las décadas de 1960 y 1980 y muchas conducciones han alcanzado o se aproximan al final de su vida útil. Mientras las necesidades de renovación se sitúan, según los datos recogidos, en torno al 2 % anual, la inversión actual ronda el 0,4 %. La edad media de las redes de abastecimiento es de aproximadamente 40 años.

Renovar menos de lo necesario no solo implica aplazar una obra. El envejecimiento de las redes se relaciona con problemas de servicio, de salud pública, costes económicos, impacto ambiental, escasez de agua y pérdida de eficiencia hidráulica y energética. Frente a una estrategia basada principalmente en reparar cuando aparece una avería, la propuesta pasa por planificar la renovación con una visión más amplia y a largo plazo.

Ahí aparece una alternativa que propone intervenir bajo tierra sin necesidad de abrir grandes zanjas: las tecnologías sin zanja, conocidas como TSZ. Su objetivo es rehabilitar, renovar o instalar conducciones, reduciendo las actuaciones en superficie. No se trata de una única técnica, sino de un conjunto de soluciones que incluye sistemas como el bursting, las mangas, el spray lining o la perforación dirigida.

La diferencia con una obra convencional puede entenderse al observar lo que ocurre cuando se abre una calle. El método tradicional requiere excavar, preparar el lecho de la zanja, instalar la tubería, realizar los anclajes, rellenar y compactar y, después, reponer la superficie. Las TSZ permiten reducir o evitar gran parte de estas operaciones. Menos tierra que mover también significa menos transporte, menos maquinaria, menos reposiciones y menos tiempo de ocupación de la vía pública.

La cuestión no afecta únicamente a la comodidad de quienes circulan por la ciudad. Una obra con zanjas puede modificar itinerarios, generar atascos, producir polvo, afectar a los comercios y aumentar el tiempo que los ciudadanos dedican a sus desplazamientos. Estos factores deben considerarse al analizar los llamados costes sociales de una intervención.

Los números de uno de los estudios recogidos por Verdú y Gázquez (2025) ilustran la diferencia. Para el proyecto analizado, los costes sociales alcanzan los 8.183 dólares por metro con el método tradicional, frente a los 384 dólares por metro con la tecnología sin zanja. La distancia entre ambas cifras es de 21 veces. En el apartado ambiental, la diferencia es menor, aunque también favorable a las TSZ: 288,7 dólares por metro frente a 390,2, lo que supone un ahorro del 35 %.

El impacto en el entorno también se relaciona con la cantidad de materiales y recursos que requiere una obra. Las tecnologías sin zanja reducen el movimiento de tierras y el transporte a vertederos autorizados, disminuyen las necesidades de asfaltado y reposición y pueden reducir el movimiento de maquinaria y el consumo de combustibles fósiles. Estos factores se relacionan con una menor emisión de dióxido de carbono.

La seguridad constituye otro de los argumentos utilizados para defender este tipo de intervención. El material advierte sobre los riesgos asociados a las zanjas y señala que en Europa se registran 120 muertes y 6.000 heridos cada año. Frente a esas condiciones, las TSZ se presentan como una alternativa que permite reducir los accidentes laborales y las afectaciones a otros servicios subterráneos. También ofrecen una menor dependencia de las condiciones meteorológicas y pueden reducir los costes y la duración de las obras.

El beneficio puede ser especialmente visible en una ciudad en funcionamiento continuo. Allí donde una excavación podría obligar a cortar una calle y alterar el tráfico, una intervención subterránea busca mantener la actividad urbana mientras se trabaja bajo tierra. El planteamiento es sencillo: reparar la infraestructura sin que la ciudad tenga que detenerse.

Murcia utiliza estas tecnologías desde hace más de dos décadas. La experiencia de Aguas de Murcia incluye fresado, bursting, mangas Packers y perforación dirigida, además de soluciones incorporadas posteriormente como spray lining y distintos sistemas de mangas. La empresa plantea como objetivo potenciar estas técnicas y convertirlas en la primera opción para la rehabilitación.

Los datos aportados permiten medir la evolución de esta apuesta. La red de saneamiento de Murcia alcanza los 1.634 kilómetros, de los cuales el 1,9 % ha sido rehabilitado mediante tecnologías sin zanja. El gasto anual destinado a estas actuaciones pasó de 466.000 euros en 2019 a 900.000 euros en 2024. La longitud media rehabilitada es de 2.800 metros al año.

Los casos prácticos muestran que no existe una única forma de aplicar estas tecnologías. En la plaza de Santa Eulalia, junto a un conjunto amurallado histórico, se rehabilitaron 75 metros de un colector de 600 milímetros mediante manga ultravioleta. El objetivo era resolver las filtraciones y recuperar las características de la conducción sin recurrir a una excavación convencional.

Uno de los proyectos descritos afecta al colector S1, infraestructura crítica para el transporte de aguas residuales hacia la estación depuradora. La conducción, muy deteriorada, recoge aguas de más de ocho pedanías y barrios de Murcia y pasa por debajo de una plataforma ferroviaria. En este caso se utilizó el sistema bursting para introducir una tubería de polietileno de 800 milímetros y rehabilitar 600 metros de conducción.

Otro ejemplo es el colector ovoide de Santa Cruz, una conducción muy deteriorada que discurre por una carretera de alto tráfico. Se rehabilitaron 95 metros mediante un sistema de manga UV. También en Puente Viejo se recurrió a una solución diferente: 75 metros de una conducción de fundición de 450 milímetros fueron renovados internamente mediante resina de poliurea aplicada con Spray Lining.

Las técnicas también se han utilizado para prevenir posibles afectaciones al medio natural. En la impulsión de Alquerías, situada a su paso por el río Segura, se rehabilitaron 50 metros de una conducción de 400 milímetros mediante una manga por columna de agua. El problema planteaba la posibilidad de vertidos al río y de elevados costes de reparación. El resultado descrito fue un tramo completamente rehabilitado y estanco.

No todos los argumentos a favor de las TSZ son económicos o técnicos. También se plantea la cuestión de cómo decidir qué infraestructuras renovar y cuándo. Las tarifas limitadas, la búsqueda de retornos rápidos y la preferencia por el mantenimiento correctivo pueden obstaculizar las inversiones necesarias para renovar las redes. La propuesta consiste en valorar las actuaciones pensando también en sus efectos a medio y largo plazo.

Esa decisión tiene, además, una dimensión ciudadana. Es necesario explicar a la población qué hay detrás de las tarifas y de las inversiones en las redes de agua. Mantener precios bajos puede entrar en conflicto con la necesidad de financiar la renovación de infraestructuras envejecidas. Para los autores del material, la sostenibilidad requiere combinar los objetivos económicos, ambientales y sociales.

La discusión cambia cuando se contabiliza el coste total de una obra. El precio de construir una conducción es solo una parte de la factura. También existen costes derivados del tráfico, del consumo de combustible, de los residuos, de las reposiciones, de las molestias a los ciudadanos o de la actividad comercial. Estos factores deberían formar parte de la comparación entre las alternativas.

El reto, por tanto, no consiste simplemente en elegir entre una zanja y una tecnología distinta. Se trata de decidir cómo las ciudades quieren renovar sus infraestructuras envejecidas sin interrumpir su actividad cotidiana. Las tecnologías sin zanja ofrecen una vía que reduce la intervención en la superficie y que, según los datos recopilados, puede aportar ventajas económicas, ambientales y sociales.

La experiencia de Murcia muestra que esas técnicas ya forman parte de la gestión de sus redes. Además, todo apunta a una expansión de su uso, especialmente en el marco de una estrategia vinculada a la economía circular. Para que esa transformación avance, plantea dos condiciones: valorar todos los costes e impactos de cada proyecto y continuar desarrollando soluciones que reduzcan los costes de construcción.

Las tuberías seguirán ocultas bajo las calles. La diferencia puede estar en cómo se decide repararlas cuando envejecen. Frente a la imagen tradicional de una ciudad levantada por una zanja, las tecnologías sin zanja proponen otra posibilidad: intervenir bajo tierra y mantener, en la medida de lo posible, la ciudad en funcionamiento sobre ella.

Aquí tenéis un vídeo que os he grabado al respecto. Espero que os resulte de interés.

En este vídeo se resumen las ideas más interesantes de este tema.

Referencia:

Verdú, C., & Gázquez, P. (2025). Las TSZ 1.ª opción social, medioambiental y económica [Material del XI Curso de Postgrado Especialista en Tecnologías Sin Zanja]. Aguas de Murcia.

Licencia de Creative Commons
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Ejecución de la Perforación Horizontal Dirigida

1. Introducción

La Perforación Horizontal Dirigida, (PHD) es una técnica que requiere coordinar equipos, herramientas, fluidos, sistemas de navegación y tuberías en una secuencia constructiva previamente definida. El documento (Pintó Bascompte, 2025) organiza esta secuencia en torno a tres operaciones principales: perforación piloto, ensanche del túnel y pull back, o tiro de la tubería.

El proceso comienza con la preparación adecuada del emplazamiento y la adopción de las medidas de seguridad y protección medioambiental correspondientes. Después, se ejecuta la perforación piloto siguiendo el trazado establecido, se amplía el diámetro del túnel mediante una o varias operaciones de ensanche y, finalmente, se introduce la tubería. Cada etapa utiliza herramientas y parámetros específicos, pero todas forman parte de una misma operación constructiva.

El éxito de la ejecución depende de mantener bajo control la trayectoria, las condiciones del terreno, el fluido de perforación, las fuerzas de tiro y el comportamiento de la tubería. La guía también considera la comunicación entre los distintos puestos de trabajo, la gestión de residuos y de fluidos y la limpieza final del emplazamiento como componentes de la ejecución de la obra.

2. Seguridad durante la ejecución

La PHD presenta riesgos asociados tanto a la maquinaria como a las condiciones generadas por la propia perforación. Entre los peligros identificados en la guía figuran el deslizamiento provocado por el mud de perforación y el riesgo para las vías respiratorias debido al polvo de bentonita. También se consideran la manipulación de cargas suspendidas, los varillajes y los escariadores, así como los trabajos en superficies inclinadas.

Las conexiones del ensamblaje de perforación pueden estar sometidas a pares elevados durante las operaciones de apriete y aflojamiento. La guía también presta atención a la comunicación entre la cabina de control, la zona de la máquina perforadora y el lugar donde se ubica la tubería. Esta comunicación permite coordinar las operaciones que se llevan a cabo simultáneamente en distintos puntos de la obra.

La seguridad debe mantenerse durante toda la ejecución. La identificación de los servicios existentes, las infraestructuras enterradas, los accesos, los edificios próximos y otros elementos del entorno forma parte de la información necesaria para trabajar de manera controlada. También deben considerarse las posibles municiones o artefactos explosivos sin detonar presentes en la zona de trabajo.

3. Protección medioambiental

La ejecución de una PHD genera materiales excavados y fluidos que deben gestionarse adecuadamente. El procedimiento para la eliminación de detritus y del fluido de perforación debe estar definido en la planificación de la obra. Durante la perforación se controlan el volumen de detritus, el fluido y las condiciones hidráulicas en el túnel.

La protección del terreno comienza durante la instalación y continúa hasta la restitución final del emplazamiento. Las capas de terreno retiradas deben conservarse adecuadamente y, cuando sea necesario, separarse para permitir su restitución posterior conforme a su disposición original.

Los posibles derrames de aceites, gasóleos o grasas requieren medidas específicas. La zona de trabajo debe disponer de medios para absorber estos productos en caso de derrames imprevistos. El almacenamiento y la manipulación del fluido de perforación también deben realizarse de manera que se reduzcan los riesgos de contaminación.

4. Instalación de la obra

La instalación de los equipos debe realizarse conforme a la disposición prevista para el proyecto. La perforadora, los equipos auxiliares, las zonas destinadas al fluido de perforación y los espacios necesarios para preparar la tubería deben organizarse de modo que permitan ejecutar las distintas operaciones con seguridad.

Para instalaciones de mayor tamaño puede ser necesaria una grúa móvil con capacidad suficiente para manipular los equipos. La existencia de accesos adecuados y de una zona de trabajo segura condiciona la instalación. También deben excavarse y asegurarse las catas destinadas al mud.

La preparación del emplazamiento incluye las conexiones de suministro externo y la coordinación de las comunicaciones necesarias para responder a posibles emergencias. De este modo, la instalación constituye la primera fase física de la ejecución y prepara las condiciones para iniciar la perforación.

5. Perforación piloto

La perforación piloto constituye la primera de las tres operaciones básicas de una PHD. Durante esta fase, un cabezal de perforación se desplaza a lo largo del trazado previsto mientras la perforadora permanece en superficie. La fuerza de tiro y el par generados por la máquina se transmiten al cabezal a través de las varillas.

El primer conjunto ubicado dentro del túnel se denomina BHA (Bottom Hole Assembly). Según la guía, está formado por el tricono de perforación, el bent sub o adaptador inclinado y las varillas no magnéticas.

Direccionabilidad de la perforación (Bottom hole assembly)

El conjunto se introduce en el terreno con el ángulo de entrada previamente establecido. El fluido de perforación, constituido por una suspensión de agua y bentonita, circula por el interior de las varillas hasta las boquillas del tricono, desde donde sale a presión. Parte del suelo disgregado se desplaza, mientras que la mayor parte es transportada hacia la superficie por el fluido que circula en el espacio anular.

La perforación avanza mediante la incorporación sucesiva de varillas. Cada nueva varilla permite prolongar el ensamblaje y continuar la trayectoria hasta que el cabezal alcance la cata de destino. La precisión alcanzada en esta fase condiciona las operaciones posteriores.

Cabeza de perforación tricono. http://www.sondeosmar.es/

6. Herramientas para la perforación piloto

La herramienta utilizada depende de las características del terreno. Para terrenos suaves y sueltos se emplea el Jet Bit o tricono jet. Su funcionamiento se basa en la acción hidráulica del fluido que sale por las boquillas y actúa sobre el terreno situado delante de la herramienta.

Jet bit. https://www.youtube.com/watch?v=cl8BBoCV7gU

Los triconos jet roller actúan sobre la roca mediante elementos mecánicos. Su configuración incluye brazos, asientos de los jets, rodillos y cojinetes. La guía relaciona estos elementos con la codificación IADC de las herramientas de perforación.

Para formaciones más duras se utilizan motores de lodos que proporcionan el par necesario. El control direccional se consigue mediante una varilla corta y angular, el bent sub, situada entre el ensamblaje y el motor. Para rocas densas y muy duras se contemplan herramientas con insertos de metal duro TCI.

7. Ensanche de la perforación

Una vez que la perforación piloto ha alcanzado la cata final, el tricono y la sonda se desmontan y se sustituyen por un escariador. Su finalidad es aumentar el diámetro del túnel hasta alcanzar las dimensiones requeridas. El diámetro final puede obtenerse mediante varias pasadas de ensanche.

La herramienta se selecciona según el terreno. En terrenos blandos se utilizan fly cutters; en terrenos de dureza media y alta, se emplean barrel reamers y, en formaciones rocosas, hole openers. Durante el escariado se tira de la herramienta hacia atrás mientras gira y se inyecta fluido de perforación.

Los Barrel Reamers presentan un cuerpo cilíndrico de acero con forma de barril y boquillas delanteras y traseras. Los Fly-Cutters tienen una configuración abierta formada por un anillo de corte conectado a una varilla central mediante varios puntales. Las boquillas pueden encontrarse en el anillo o en los puntales.

La herramienta de ensanche debe mantenerse alineada con el túnel previamente perforado. Para ello pueden utilizarse estabilizadores y centralizadores. El procedimiento convencional es el back reaming, en el que el escariador se tira desde el lado de la tubería hacia la máquina. También puede emplearse el push reaming, en el que el escariador se empuja desde la máquina hacia el terreno.

8. El fluido de perforación

El fluido de perforación es uno de los elementos técnicos principales de la PHD. La guía establece controles para la densidad, la viscosidad, el pH, el volumen de circulación y el contenido de sólidos.

Para un fluido compuesto por agua y bentonita, la densidad indicada se sitúa entre 1,02 y 1,06 g/cm³. En el fluido de retorno se establece un máximo del 30 % de sólidos en suspensión.

La viscosidad se controla mediante el Marsh Funnel. Para terrenos arcillosos se indican valores de 30 a 40 segundos; para arena cohesiva, de 35 a 40 segundos; para arena no cohesiva, de 45 a 60 segundos; para arena gruesa, de 60 a 80 segundos; y para grava gruesa, valores superiores a 80 segundos.

El pH de la bentonita debe situarse entre 8 y 10. El volumen de circulación, expresado en litros por minuto, debe controlarse y registrarse continuamente. Este registro permite detectar pérdidas o disminuciones del fluido durante la ejecución.

El retorno continuo del lodo permite controlar las condiciones hidráulicas del túnel. La guía relaciona la prevención de presiones excesivas con el mantenimiento del espacio anular, el aumento de la cobertura cuando sea necesario, la ejecución de perforaciones o catas destinadas a aliviar la presión, la adaptación del lodo a la geología y el control permanente de la presión y del retorno.

También deben controlarse la velocidad de perforación y las condiciones de limpieza. Después de intervalos de espera, puede ser necesario hacer girar la sarta para romper la estructura de gel del lodo. Cuando se registran intervalos prolongados, se contempla la limpieza del túnel y la eliminación de detritus.

9. Sistemas de localización y navegación

La localización del cabezal permite controlar su posición respecto al trazado previsto. La guía distingue tres sistemas: Walk-Over, Wire-Line y brújula giroscópica.

El sistema Walk-Over se utiliza en equipos de perforación de menor tamaño. Un sensor situado detrás del cabezal proporciona información sobre su posición bajo tierra y permite seguir la evolución de la trayectoria.

El sistema Wire-Line utiliza una sonda situada en el ensamblaje y conectada mediante un cable. La posición se determina mediante el campo magnético terrestre y la gravedad. La información se transmite a la cabina de control, lo que permite controlar la trayectoria durante la perforación.

La brújula giroscópica constituye otro sistema de navegación contemplado en la guía. En perforaciones de gran longitud se emplean sistemas especiales. Uno de ellos es la perforación por intersección, en la que se inicia la perforación desde ambos lados y se alinean las dos trayectorias hasta que se produce el encuentro de los BHA.

La guía registra un récord de 5,2 km en el puerto de Hong Kong asociado a este tipo de sistema. También presenta navegación paralela mediante un anillo externo parcial.

10. Construcción y preparación de la tubería

La tubería debe prepararse antes del pull back. El documento contempla cuatro materiales principales: acero, hierro fundido dúctil, polietileno y polipropileno.

Las tuberías de acero se utilizan principalmente para transportar gases y líquidos a alta presión. El hierro fundido dúctil se emplea para el agua potable y el agua residual, especialmente el residual agresivo. El polietileno y el PEAD se extruyen y suministran en longitudes continuas, limitadas principalmente por las capacidades de transporte.

Durante la preparación deben considerarse los rodillos de enfilado, el posible estirado del tubo sin rodillos y la sobretorsión. La tubería debe quedar preparada para que el tiro pueda realizarse sin introducir esfuerzos no previstos en la conducción.

El tubo preparado para el pull back se coloca normalmente sobre rodillos. Estos facilitan su desplazamiento durante el tiro y permiten controlar su posición antes de entrar en el túnel.

11. Pull back o tiro de la tubería

Una vez preparado el túnel, comienza la operación de pull back. La tubería se conecta al conjunto de perforación y se arrastra hacia la máquina mientras el escariador sigue girando.

La conexión se realiza mediante un sistema antigiro, denominado swivel, y una conexión universal. El swivel permite transmitir la fuerza de tiro sin transmitir al tubo el par de rotación generado por la herramienta.

El control de esta operación incluye el registro de los parámetros del pull back y la detección de las fuerzas de tiro. La guía incorpora estos datos en la documentación que debe aportar el contratista.

12. Sobretorsión y comportamiento de la tubería

La geometría de salida condiciona la disposición de la tubería durante el pull back. El documento dedica un apartado específico a la sobretorsión y a los elementos empleados para preparar el tubo. Entre ellos figuran los rodillos, las placas deslizadoras y las condiciones de tiro, con o sin rodillos.

El comportamiento de la tubería dentro de la perforación también depende de su interacción con el fluido. La guía expresa esta condición mediante dos situaciones: cuando E < P, el tubo arrastra por el fondo del microtúnel; cuando E > P, arrastra por la parte superior. El documento relaciona estas condiciones con el cálculo de la suspensión.

La preparación de la tubería debe considerar simultáneamente las fuerzas de tracción y de torsión, así como su comportamiento en el túnel. Por ello, las tensiones de la tubería, las fuerzas de tiro y la torsión forman parte de los datos que deben definirse y controlarse durante el proyecto.

13. Cementación y control de fugas de lodo

El espacio anular entre la pared del túnel y la tubería principal debe cementarse cuando exista riesgo de asentamiento o drenaje, o cuando exista una diferencia importante de altura entre la entrada y la salida. La guía menciona, como ejemplos, los cruces de líneas ferroviarias y de diques.

Durante la cementación debe rellenarse completamente el espacio anular. Los materiales de aislamiento deben mantenerse en contacto con la pared del túnel sin retroceso, manteniendo las condiciones requeridas en el espacio existente alrededor de la conducción.

Las fugas de lodo requieren un control continuo, ya que alteran las condiciones hidráulicas del túnel. Su prevención se relaciona con la presión, el retorno del fluido, la velocidad de perforación, la limpieza del anular y la adaptación del fluido a las condiciones geológicas.

14. Limpieza y restitución de la obra

Una vez finalizada la instalación, la obra debe limpiarse y quedar lista para su aceptación o recuperación. La guía contempla la limpieza de la máquina, el engrase de las varillas y la protección de sus roscas.

También deben desmontarse los mecanismos e instalaciones auxiliares, retirarse las líneas de suministro externo y eliminarse los residuos del fluido de perforación y otros residuos selectivos. Las instalaciones retiradas temporalmente deben restituirse y los accesos repararse.

La actuación final consiste en dejar el emplazamiento en condiciones adecuadas para su aceptación por el propietario o sus representantes legales.

15. Lectura integrada del proceso de ejecución

La PHD debe estudiarse como una secuencia en la que cada operación prepara la siguiente. La perforación piloto establece la trayectoria; el ensanche transforma esa trayectoria en un túnel con el diámetro requerido; y el pull back utiliza ese túnel para introducir la tubería.

Las herramientas se seleccionan en función del terreno, mientras que el fluido se controla en función de las condiciones del terreno. La navegación permite conocer la posición del cabezal y mantener la trayectoria. La preparación de la tubería, los rodillos, el control de la sobretorsión y las fuerzas de tiro permiten completar la instalación.

El proceso constructivo concluye con el control de las condiciones finales, la retirada de los equipos, la gestión de residuos y la restitución del emplazamiento. La ejecución de una PHD comprende, por tanto, tanto la creación del túnel como todas las operaciones necesarias para instalar la tubería y devolver la zona a condiciones aceptables.

Referencia:

PINTÓ BASCOMPTE, J.D. (2026). Módulo M7-2 del Curso de Postgrado Especialista en Tecnologías Sin Zanja, Parte 2.

 

Planificación en la Perforación Horizontal Dirigida (PHD)

1. Introducción: qué es la Perforación Horizontal Dirigida

La Perforación Horizontal Dirigida, PHD, conocida también por sus siglas en inglés, HDD (Horizontal Directional Drilling), es presentada en el material como un sistema constructivo sin zanja. La secuencia básica consiste en realizar primero una perforación guía dirigida, ejecutar después el ensanche de la perforación e introducir finalmente la tubería definitiva desde el lado de salida. El documento (Pintó Bascompte, 2025) sitúa esta técnica dentro de un rango de microtúnel comprendido entre Ø 60 mm y 1600 mm.

La PHD se describe como un método rápido, limpio y ecológico que permite instalar servicios como el agua, el gas, la electricidad y las comunicaciones. También permite instalar tuberías por debajo del nivel freático y se relaciona con trabajos de descontaminación de suelos, así como con la reconstrucción y la ampliación de colectores. El principio didáctico que organiza todo el capítulo es sencillo: antes de instalar hay que planificar.

La guía se estructura en cuatro grandes bloques: principios del proyecto, geología y subsuelo, autorizaciones y planificación del proyecto. Para valorar la viabilidad de una PHD se necesita información básica que normalmente entrega el cliente, especialmente documentación relativa a la topografía y a la geología del área próxima a la obra.

www.flowtex.com.ar

2. Información inicial necesaria para definir el proyecto

2.1. Plano de ubicación general

El plano de ubicación general permite situar las vías de acceso, la obra, la tubería, las zonas de almacenaje y de ensamblaje del tubo, y otras instalaciones necesarias para la construcción. La escala indicada en el material se sitúa entre 1:5.000 y 1:25.000. Su función es proporcionar una visión territorial del conjunto de la actuación y de los espacios que deberán utilizarse durante la ejecución.

2.2. Vista en planta

Para estudiar la geometría de la perforación prevista se necesita un plano fiable y detallado en planta. Debe permitir valorar la longitud de la perforación, la distancia respecto de los edificios circundantes y la anchura de las estructuras existentes o previstas en el subsuelo. La información debe relacionarse, cuando proceda, con la fecha de la cartografía o de los mapas cartográficos relevantes. La escala indicada es de 1:500 a 1:1.000. El material muestra, como ejemplos, una vista en Google Earth, una representación en AutoCAD y una ortofoto.

Catalana de Perforacións, S.A.

2.3. Sección transversal y perfil

Para determinar el perfil de la perforación se necesita información sobre las cotas del terreno a lo largo de la trayectoria prevista. También deben considerarse las distancias a zonas concretas y a posibles obstáculos. El documento recomienda referir la información de las secciones longitudinales a la fecha de la cartografía o de los mapas cartográficos relevantes, de ámbito nacional, y señala una escala de 1:100 a 1:250.

Catalana de Perforacións, S.A.

2.4. Profundidad de arroyos y ríos

Cuando se deba cruzar un arroyo o un río y no se disponga de datos sobre su profundidad, debe realizarse una batimetría o disponer de series de profundidades para determinar el nivel del fondo del río o del mar. El material considera esta información necesaria para diseñar una distancia de seguridad y garantizar un fondo aceptable y seguro entre la masa de agua y el túnel.

2.5. Mapas históricos

Los mapas históricos adquieren especial interés en zonas donde exista una alta probabilidad de encontrar objetos arqueológicos anteriores a los planos de infraestructura actuales. También pueden revelar infraestructuras antiguas que ya no figuran en la documentación disponible. Por ello, la investigación previa no debe limitarse a la cartografía contemporánea.

2.6. Infraestructuras y servicios existentes

Si existen cables, tuberías, conductos u otros servicios próximos al cruce, deben identificarse su posición exacta, sus especificaciones y el medio que transportan o suministran. Esta información es relevante tanto cuando los servicios se cruzan con la perforación como cuando discurren en paralelo a una distancia inferior a 20 m. Antes de comenzar la construcción, el contratista debe comprobar los resultados de estas investigaciones y contrastarlos con las autoridades locales y los proveedores de servicios.

El material fija, además, una distancia de seguridad entre la PHD piloto y los servicios existentes: debe ser de dos veces el diámetro de la PHD respecto del eje de la perforación piloto y de la parte exterior del servicio, con un mínimo de 50 cm respecto de la parte exterior del último escariado. Esta condición debe incorporarse al trazado y al control geométrico de la perforación.

Catalana de Perforacións, S.A.

2.7. Cimentaciones y otras infraestructuras

Cuando existan obras de ingeniería civil próximas al cruce, o vestigios de ellas en forma de túneles, cimentaciones u otros trabajos, deben determinarse e identificarse su posición exacta y sus dimensiones. La distancia mínima entre el eje de la perforación PHD y cualquier otra estructura no debe ser inferior a 2 m.

2.8. Datos climáticos e hidrográficos

Según la región, la climatología puede condicionar la planificación. Deben considerarse la distribución y la cantidad de las precipitaciones, la temperatura, la frecuencia de las fluctuaciones y los valores absolutos. Para los datos hidrográficos deben contemplarse las condiciones generales y la amplitud de las mareas.

Cuando se emplee agua corriente, de río, de canal o subterránea para preparar el fluido de perforación, se requieren datos sobre su calidad. El material identifica como parámetros de interés el pH, la salinidad, la alcalinidad y la dureza. El pH se define como una medida de la acidez o alcalinidad de una disolución y como indicador de la concentración de iones de hidrógeno; se proporciona como referencia un valor de pH entre 8 y 10. La salinidad se define como el contenido salino en suelos o agua y se relaciona con la conductividad eléctrica; se considera un valor inferior a 750 µS/cm como referencia. El material también menciona como unidades mhos/cm o Siemens.

3. Geología y subsuelo

La investigación del subsuelo tiene dos objetivos directos: evaluar la viabilidad del proyecto y reducir los riesgos geológicos. El material establece que una persona experta debe planificar las investigaciones, supervisar las actividades realizadas in situ y en el laboratorio, y redactar el informe geotécnico. El alcance de la investigación depende de las condiciones geográficas y geológicas, así como de los datos del proyecto. Cuando existen condiciones geológicas poco habituales o estructuras del terreno más complejas, debe realizarse una investigación más extensa.

3.1. Clasificación y evaluación de documentos existentes

Deben estudiarse los mapas y los materiales disponibles, incluidos los mapas geológicos, las secciones, los registros de perforación y los perfiles. También deben aprovecharse de las investigaciones geotécnicas realizadas para construcciones anteriores, como puentes y cimentaciones, siempre que se encuentren en las inmediaciones del proyecto.

3.2. Investigación histórica

La investigación histórica debe considerar las inmediaciones del proyecto de PHD, especialmente las zonas industriales próximas, las edificaciones anteriores y las construcciones abandonadas. También debe incluir posibles hallazgos arqueológicos o áreas identificadas como potencialmente relevantes, aunque las autoridades locales no siempre hayan comunicado su existencia. Además de revisar los archivos disponibles, el material considera obligatoria, en términos profesionales, una visita de obra. La investigación también debe contemplar la posibilidad de encontrar municiones y explosivos sin detonar.

3.3. Sondeos

Para conocer las condiciones del terreno, se realizan sondeos verticales para recuperar testigos. El material indica intervalos de 50 a 100 m, en orden alternado, con los sondeos situados aproximadamente a 5 m de la línea central de la trayectoria prevista. La profundidad debe situarse entre 2 y 5 m por debajo del nivel inferior del perfil de perforación proyectado. Estos intervalos deben respetarse especialmente en los tramos próximos al agua.

Entre los métodos de sondeo se enumeran la perforación rotativa con recuperación de testigo, la perforación helicoidal, la perforación a percusión y la perforación vibrocore. Para obtener muestras se citan tres procedimientos habituales: recuperación continua de muestras del núcleo, recuperación continua de muestras fuera del núcleo y obtención de muestras de suelo incompletas.

3.4. Ensayos de penetración: SPT

Los ensayos de penetración se realizan en las inmediaciones de la perforación y sirven para determinar parámetros del suelo, como la compactación en suelos de baja cohesión o la consistencia en suelos de alta cohesión, y para identificar límites dentro de la estructura de los estratos.

El Test de Penetración Estándar (SPT, Standard Penetration Test) mide la resistencia del suelo a la penetración de un muestreador estándar. El ensayo utiliza un martillo de 63,5 kg que cae desde una altura de 76 cm. El muestreador tiene un diámetro exterior de 50,8 mm, equivalente a 2 pulgadas. El resultado principal es el valor N o número de golpes SPT, que representa la resistencia a la penetración del terreno. El muestreador estándar, también denominado muestreador partido o split spoon sampler, presenta dimensiones normalizadas según ASTM D1586 o UNE 103-800.

La ejecución del SPT se divide en tres fases de 15 cm cada una. Primero se hinca el muestreador 15 cm para atravesar el suelo alterado por la perforación; estos golpes no se contabilizan. Después, se realiza una primera medición de otros 15 cm y se registra el número de golpes. Finalmente se ejecuta una segunda medición de 15 cm y también se registra el número de golpes. El valor N se obtiene sumando los golpes de las dos últimas fases: N = N2 + N3. El muestreador penetra 45 cm en total, pero solo los últimos 30 cm se emplean para calcular N.

3.5. Investigaciones geofísicas

Las investigaciones geofísicas sirven para verificar los resultados y los datos obtenidos mediante las investigaciones del subsuelo. Su tipo y alcance dependen de las condiciones geológicas identificadas mediante sondeos y ensayos de penetración, así como de las condiciones locales, entre ellas el nivel del suelo, el uso de la zona y los efectos de los alrededores. Los procedimientos geofísicos pueden ejecutarse desde tierra o desde medios acuáticos. El material cita dos técnicas: el reflejo electromagnético, o georradar, y la tomografía eléctrica.

3.6. Pruebas de laboratorio

Las muestras obtenidas en las investigaciones in situ deben analizarse en el laboratorio. Para suelos no cohesivos e inconsolidados se citan, como mínimo, ensayos sobre el tamaño y la distribución de las partículas, la forma de las partículas, la densidad relativa, el ratio de compactación y la permeabilidad. Para las capas examinadas y los suelos cohesivos se indican la forma estructural y apariencia y los límites líquido y plástico de Atterberg.

Pueden ser necesarias pruebas adicionales cuando existan condiciones específicas, como las arcillas expansivas. En la roca, las discontinuidades, las cavidades y los efectos del desgaste pueden influir significativamente en su comportamiento de ingeniería. Por ello, se indican ensayos sobre la estructura de la roca, incluyendo la estratificación y las fisuras, el estado de desgaste, la resistencia a tracción y la resistencia a compresión simple.

3.7. Informe geotécnico

El informe geotécnico permite al ingeniero cualificado o al contratista evaluar la viabilidad de perforar a través de las capas del terreno. Debe recoger las características del terreno relacionadas con el uso de la PHD, la información relevante sobre el suelo para evaluar los fluidos de perforación, incluida la permeabilidad de la formación, los registros de perforación y los resultados de las pruebas de penetración, la información geofísica y su ubicación, las pruebas geofísicas, la información histórica y la presencia de obstrucciones o anomalías geológicas cuando existan. La sección geológica no debe representarse a escala exagerada ni distorsionada.

4. Autorizaciones

El material dedica un apartado específico a las autorizaciones y diferencia la participación del cliente de la del contratista. Las diapositivas disponibles en este módulo presentan a estos dos responsables en apartados separados, pero no establecen una relación concreta de permisos, organismos, trámites ni documentos administrativos. Por ello, este capítulo conserva esa información sin añadir requisitos externos que no figuran en el material.

5. Planificación del proyecto

La planificación del proyecto se divide en principios básicos, planos, cálculos y planificación de la construcción. El establecimiento del perfil de perforación entre los puntos de entrada y de salida es uno de los elementos centrales. Para que el perfil diseñado pueda ejecutarse, deben comprobarse el trazado, los radios de curvatura, el diámetro del túnel y las tolerancias.

5.1. Trazado y ángulos de entrada y salida

Los ángulos de entrada y salida deben ajustarse al radio de curvatura de la tubería a instalar. El material sitúa estos ángulos entre 6° y 15°, según el equipo de perforación seleccionado. Como regla general indicada en la guía, el ángulo debe ser más plano cuanto mayor sea el diámetro de la tubería.

El ángulo de entrada puede ser más inclinado cuando no sea necesario que el personal trabaje en la máquina, como en trabajos de perforación pequeños. El ángulo de salida puede ser más inclinado cuando los tubos presentan un radio de curvatura menor, por ejemplo, en las tuberías de PE, lo que da lugar a una inclinación menor o a una mayor arqueada en el punto de salida.

5.2. Secciones rectas de entrada y salida

Los primeros y últimos tramos de la perforación deberían ser rectos y debe evitarse introducir un radio de perforación en esas zonas. Se trata de áreas con poca profundidad de cobertura y menor compactación, por lo que un suelo inestable suele ser poco adecuado para ejecutar curvas en las secciones de entrada y salida. La longitud de los tramos rectos depende de las dimensiones del túnel, del peso y de la rigidez del ensamblaje del extremo del túnel, BHA (Bottom Hole Assembly). Cuanto mayor sea el túnel y cuanto más pesado y rígido sea el ensamblaje de fondo, más largos deberían ser estos tramos. El primer tramo de la línea de perforación debe ser lo más largo posible y tener, como mínimo, la longitud de dos varillas de perforación.

5.3. Cobertura

La cobertura es la distancia entre el extremo de la tubería y la superficie, el lecho de un río o el fondo del mar. Debe calcularse una cobertura mínima en función de las condiciones del suelo para evitar la rotura del lodo. Según el material, la cobertura debería ser igual al diámetro del tubo multiplicado por un factor comprendido entre 10 y 15. Así, para una tubería de 800 mm, la cobertura en zonas de agua debería ser de 8 a 12 m.

Las coberturas inferiores a 5 m que puedan resultar de aplicar esa regla a tuberías de menor diámetro deben valorarse críticamente y caso por caso. Para carreteras principales, autopistas y otros obstáculos que deban cruzarse, se indican valores de cobertura similares. En los cruces de carreteras deben consultarse las normas nacionales adicionales, la información específica y las aprobaciones requeridas por la entidad correspondiente. También existen normas nacionales adicionales para los cruces de vías férreas. El material relaciona una mayor profundidad de cobertura con una menor probabilidad de rotura de lodo y de colapsos subterráneos.

5.4. Radio de curvatura

El radio mínimo de curvatura admisible desempeña un papel decisivo en el diseño del perfil. Debe diferenciarse entre el radio mínimo permitido por las varillas de perforación y el permitido por la tubería a instalar. Para perforaciones pequeñas y tuberías de PE, la guía indica que el radio mínimo suele determinarse por el radio de las varillas. En perforaciones grandes y con tubos de acero, el radio mínimo de la línea de tubería puede determinar el diseño. Cuando el varillaje determina el radio mínimo, el perfil puede calcularse con los valores recomendados por el fabricante. Como guía, se propone asumir radios de entre 30 y 250 m.

La trayectoria se determina conjuntamente a partir del ángulo de entrada, del desplazamiento y de la profundidad mínima, respetando los límites de curvatura. El material plantea el cálculo del desplazamiento B y de la inclinación de entrada A necesarios para alcanzar una profundidad mínima D y remite a una tabla de cálculo incluida en la presentación.

5.5. Sobre torsión

Durante el pull-back, cuando la tubería se introduce en el túnel, la línea describe una curva dentro de la perforación antes de pasar al tramo recto. Esta zona se denomina sobre torsión. El material indica que, durante la operación de tiro, la presión en la sobre torsión es cero, por lo que el valor de corrección de seguridad puede reducirse a S = 1,3. La presentación muestra una ecuación de Mohr para el radio mínimo de curvatura de la sobre torsión y define Rmin como radio de torsión mínimo permisible, Da como diámetro exterior del tubo y K como límite de elasticidad mínimo.

Por razones prácticas relacionadas con la rigidez de la tubería, sobre todo en grandes diámetros, debe escogerse un radio mayor en la sobre torsión. Como valor de referencia, se propone un radio, expresado en metros, igual a 0,8 veces el diámetro de la tubería, expresado en milímetros. Para un tubo de 800 mm, el ejemplo del material da un radio de sobre torsión de 640 m.

5.6. Radios combinados

Cuando además de una curva vertical existe una curva horizontal, el radio combinado es menor que el radio horizontal o que el radio vertical. El radio combinado se define como el radio aplicable o efectivo a la curva de la tubería. Para planificar y ejecutar la perforación, el radio mínimo calculado debe compararse con el radio mínimo permitido para los radios combinados.

5.7. Diámetro del túnel y espacio anular

El espacio anular expresa la relación entre el diámetro de la tubería y el diámetro de la perforación. Para calcularlo debe tomarse como referencia el mayor diámetro de la tubería, especialmente en las zonas de juntas o uniones, como puede ocurrir con tubos de acero fundido o con manguitos electrosoldables. Un espacio anular adecuado permite un pull-back suave de la tubería dentro del túnel perforado.

El material indica factores aceptables para calcular un anular adecuado de 1,2 en suelos estables y de 1,5 en suelos inestables.

5.8. Tolerancias

En la perforación piloto se establecen varias tolerancias generales. Salvo en los puntos de entrada y salida, las desviaciones del perfil respecto del trazado previsto en cada dirección no deben superar el 10 % del máximo de posición lateral y de profundidad. La desviación del radio del agujero respecto del radio de diseño no debe superar el 10 %. En el punto de entrada, la desviación indicada corresponde al diámetro del tubo multiplicado por un factor de 1, con un máximo de 0,3 m. En el punto de salida, la desviación indicada corresponde al 2 % de la longitud de la perforación, con un máximo de 5,0 m.

6. Planos del proyecto

Los planos constituyen una parte central de la planificación de una PHD. Deben incluir el tramo longitudinal, la vista en planta, la sección transversal, el trazado de la obra con la ubicación de la tubería y de la máquina, y la zona de enfilado y de tendido de la tubería sobre rodillos.

Para planificar estos proyectos son especialmente relevantes los planos de las secciones longitudinales, el mapa topográfico y las secciones transversales. En perforaciones de mayor tamaño deben prepararse también los planos del trazado de obra en los lados de entrada y salida, los planos de la zona de enfilado y sobre torsión y las zonas de expropiación temporal necesarias para la construcción.

7. Cálculos de construcción y funcionamiento

La planificación incluye cálculos diferenciados según las condiciones analizadas. Los cálculos relativos a las condiciones de construcción son responsabilidad del contratista, mientras que los relativos a las condiciones de funcionamiento son responsabilidad del cliente.

7.1. Condiciones de construcción: fuerza de tiro

Cuando se estira una tubería mediante PHD, deben responderse dos preguntas: si las tensiones producidas en la línea durante el pull-back se mantienen dentro de los niveles permitidos y si la máquina y el equipo pueden proporcionar la fuerza suficiente para instalarla. Para responderlas, hay que determinar la fuerza máxima esperada durante el pull-back.

Debe distinguirse entre las fuerzas de fricción que actúan sobre la tubería y las que debe desarrollar todo el sistema de perforación. Estas últimas son mayores porque deben superar, además, las fuerzas de fricción asociadas al conjunto formado por la tubería, el escariador y el swivel o elemento antigiro.

7.2. Fuerza de tiro en la cabeza de tiro

Durante el pull-back, una parte de la tubería ya está dentro de la perforación y otra parte permanece sobre los rodillos y fuera del túnel. La fuerza necesaria para superar la fricción sobre los rodillos depende del peso de la tubería, incluido el revestimiento, el casing y el sistema de lastre asociado a la flotabilidad del agua; del tipo y geometría de los rodillos; del tipo y estado de su superficie; del radio de la sobre torsión; de la longitud de tubería situada entre los soportes; y de las condiciones de los soportes, incluida su lubricación.

Dentro del túnel, las fuerzas necesarias para superar la fricción dependen de la fricción entre la superficie de la tubería y el fluido de perforación, de la fricción entre la superficie de la tubería y la pared del túnel y del radio combinado de la perforación. La fricción entre la tubería y el fluido depende principalmente del tipo de revestimiento y de parámetros del fluido, como la densidad, la viscosidad, la cantidad de partículas en suspensión y la velocidad del caudal en el espacio anular.

La fricción entre la tubería y la pared del túnel está condicionada por los parámetros del terreno y su coeficiente de fricción, por el lastre negativo o positivo de la línea dentro del túnel y por la geometría general de la perforación, especialmente por sus radios de curvatura.

7.3. Fuerza de tiro en la perforación

Las fuerzas que debe desarrollar la máquina perforadora son superiores a las que aparecen en la cabeza de tiro porque la máquina debe tirar del tubo y, además, del ensamblaje y del BHA, o Bottom Hole Assembly. La magnitud de la fricción depende de los parámetros técnicos de la máquina y de los componentes del ensamblaje de tiro, incluidos el equipo auxiliar, la forma de las conexiones y el peso de las varillas. La geometría del túnel también desempeña un papel importante en la fricción que se produce en las varillas.

Cuanto mayor sea el radio del túnel y cuanto más suave y preciso sea el eje perforado, menor será la fuerza de pull-back. Además, a medida que avanza la operación de pull-back, disminuye la componente de la fuerza debida a la fricción delante de la cabeza de tiro, ya que quedan menos varillas en el túnel.

7.4. Métodos de cálculo de la fuerza de tiro

El material cita dos métodos utilizados con frecuencia: la norma holandesa NEN 3651 y los métodos de la AGA, Asociación de Gas Americana. Con ambos procedimientos puede calcularse la fuerza máxima esperada en la cabeza de tiro de la línea de tubería, donde el máximo se produce, según la guía, justo antes de finalizar la operación de tiro.

También se proporciona una ecuación aproximada derivada de datos empíricos de operaciones reales: F [kN] = L × D × f × π. En ella, F es la fuerza de tiro en kN, L es la longitud de la perforación en m, D es el diámetro del tubo en m, f es el factor indicado en la tabla siguiente y π se toma como 3,14.

La tabla del material descompone el factor en seis características. Para el material del tubo, el valor es 0,3 para un material flexible, como el PE, y 0,4 para un material rígido, como el acero. Para el radio de perforación, se indica 0,5 para radio pequeño y 0,3 para radio grande. Para la suma angular, se indica 0,3 para valores inferiores a 15° y 0,5 para valores superiores a 30°. Para los obstáculos en el perfil, se indica 0,5 cuando hay alta probabilidad y 0,3 cuando hay baja probabilidad. Para un tubo perfectamente pesado, se indica 0,3 cuando la condición se cumple y 0,5 cuando no se cumple. Finalmente, para las características de fricción del suelo, se indica 0,5 para condiciones exigentes y 0,3 para condiciones estándar.

7.5. Tensiones de la línea de tubería

El cálculo de las fuerzas máximas de tiro permite determinar la capacidad necesaria de la máquina perforadora, el sistema de anclaje requerido, las tensiones en la línea de tubería durante la instalación y la torsión del tubo, considerando el radio del túnel y la fuerza de retorno.

Para el pull-back de tuberías de polietileno, deben realizarse comprobaciones de resistencia a la torsión, al aplastamiento y a la presión del fluido de perforación. Esta última puede compensarse mediante una cabeza de tiro abierta o mediante el llenado de la tubería de agua. Para la instalación pueden utilizarse cálculos basados en el módulo elástico a corto plazo.

7.6. Capacidad de la máquina perforadora

El material indica que no existe un modelo ampliamente aceptado para determinar la capacidad de la perforadora en términos de fuerza de tiro. Durante el tiro pueden producirse interrupciones prolongadas o colapsos de la perforación, por lo que las fuerzas reales pueden superar las calculadas con los modelos citados. Como valor de referencia, y dependiendo de la geología que se deba perforar, se recomienda un factor de seguridad de 2 a 3.

7.7. Capacidades del equipo de fluido

Las unidades de suministro, como las bombas de fluido de perforación de alta presión, y las capacidades de separación de la unidad deben ser capaces de suministrar o reciclar los caudales necesarios en las tres fases señaladas: perforación piloto, ensanche y pull-back.

7.8. Anclaje de la máquina

Las fuerzas de tiro de las máquinas perforadoras deben asegurarse mediante un anclaje adecuado. El material recomienda que las dimensiones del anclaje se basen en la fuerza máxima de tiro prevista. Además, el dimensionamiento debe considerar las condiciones del suelo en el que se instalará el anclaje y las condiciones geológicas del emplazamiento.

7.9. Presión del fluido de perforación

Para evitar la rotura del lodo en la superficie del terreno o en su borde superior, se recomienda calcular de forma preliminar las presiones de fluido necesarias y permitidas dentro del túnel, especialmente en perforaciones largas o en zonas sensibles. Las presiones más altas en el túnel suelen requerirse al final de la perforación piloto. Cuando sea necesario, deben planificarse y ejecutarse medidas para evitar o, al menos, controlar las roturas de lodo.

7.10. Estructuras auxiliares

Pueden ser necesarias estructuras auxiliares en proyectos especiales, por ejemplo, cuando la sobre torsión tenga un radio excepcionalmente largo o cuando el pull-back deba realizarse a lo largo de o sobre obstáculos como rutas de transporte o ríos. Estas estructuras deben planificarse e instalarse de manera coordinada con las autoridades competentes. Su dimensionamiento debe considerar todas las fuerzas y cargas efectivas.

7.11. Condiciones de funcionamiento

Para calcular las tensiones máximas del tubo durante el funcionamiento debe considerarse como una carga esencial la tensión de doblado asociada a la curvatura de la perforación. El material indica, además, que el esfuerzo tensional se sustituye por el esfuerzo derivado de la presión interna.

La comprobación de seguridad frente al doblamiento durante la fase de operación debe diferenciarse de la de la instalación. Para las tuberías de PE, debe considerarse el módulo elástico a largo plazo en lugar del módulo utilizado durante la fase de instalación.

8. Planificación de la construcción

La planificación de la construcción debe ser exhaustiva y reflejar, como mínimo, once grupos de trabajo. El primero es la investigación; le siguen la preparación de la zona, la instalación en obra, la perforación piloto, las operaciones de ensanche, la operación de pull-back, los trabajos de fabricación de la línea del tubo, la limpieza de la obra, el restablecimiento de las zonas afectadas, el despliegue del personal y del equipo y, cuando el entorno lo requiera, las medidas de drenaje.

La planificación mediante un gráfico de barras es especialmente útil cuando el día constituye la unidad mínima de tiempo. Permite representar un objetivo sencillo y comparar la situación prevista con la real, así como estimar los posibles efectos de los retrasos en el desarrollo de los trabajos. Además de estos parámetros relativos, el planning debe incluir el inicio más temprano posible de los trabajos, la finalización máxima permisible y la instalación de la tubería.

El orden de las actividades no debe interpretarse como una simple lista administrativa. Cada etapa depende de la información y de las comprobaciones anteriores: la investigación condiciona el perfil; el perfil condiciona los radios, la cobertura y el diámetro del túnel; estas variables condicionan las fuerzas de tiro; y las fuerzas de tiro condicionan la máquina, el anclaje, los equipos auxiliares y la propia seguridad de la tubería.

9. Síntesis

La idea central del módulo puede resumirse en una cadena de decisiones técnicas. Una PHD comienza antes de encender la máquina: primero se recopila la información topográfica, geológica, histórica, hidrográfica y de servicios; después se investiga el subsuelo mediante documentación, sondeos, ensayos de penetración, técnicas geofísicas y ensayos de laboratorio; finalmente, los resultados se integran en un informe geotécnico que permite valorar la viabilidad.

Con esa base se define el perfil entre la entrada y la salida. El diseño debe respetar los ángulos de entrada y salida, los tramos rectos, la cobertura, los radios de curvatura, los radios combinados, el espacio anular y las tolerancias. Los planos deben representar la geometría de la perforación y la organización física de la obra, incluidos la zona de enfilado y los espacios temporales necesarios.

Después se calculan las condiciones de construcción y de funcionamiento. Para la construcción se verifican las fuerzas de tiro, las tensiones en la tubería, la capacidad de la máquina, el anclaje, el suministro y el reciclaje del fluido, la presión del fluido y las estructuras auxiliares. Para su funcionamiento, se comprueban las tensiones asociadas a la curvatura y el comportamiento a largo plazo de las tuberías de PE.

Finalmente, la ejecución debe quedar reflejada en una planificación que contemple investigación, preparación, instalación, perforación piloto, ensanche, pull-back, fabricación de la línea, limpieza, restitución, personal y equipos, y drenaje cuando sea necesario. La guía presenta así la PHD como un proceso integrado en el que la geometría, el terreno, la tubería, la máquina, los fluidos y la organización de la obra deben ser compatibles desde la fase de proyecto.

Os dejo un vídeo que grabé en su momento al respecto.

Referencia:

PINTÓ BASCOMPTE, J.D. (2026). Módulo M7-1 del Curso de Postgrado Especialista en Tecnologías Sin Zanja, Parte 1.

 

DANA de 2024: qué nos enseñó sobre el riesgo y el diseño de nuestras infraestructuras

Cuando el agua encuentra un territorio vulnerable, una lluvia extraordinaria puede convertirse en una catástrofe. La DANA de octubre de 2024 lo demostró con una fuerza difícil de olvidar: carreteras, ferrocarriles, puentes, viviendas y redes esenciales quedaron expuestos a un episodio que puso a prueba la capacidad del territorio y de sus infraestructuras. Pero el agua no solo dejó daños; también dejó preguntas para la ingeniería. ¿Qué falló, qué funcionó y qué deberíamos cambiar para afrontar el próximo episodio extremo? La respuesta pasa por mirar más allá de la obra aislada y entender cómo territorio, hidráulica, infraestructuras, sistemas de alerta y clima interactúan cuando todo ocurre simultáneamente.

Nos adentramos en la época de lluvias. Ayer llovió con mucha fuerza en Valencia y hoy parece que sigue lloviendo. La inquietud y la memoria de lo ocurrido en fechas recientes pesan como una losa sobre quienes vivimos en estas tierras. El tiempo transcurrido permite analizar con mayor perspectiva qué factores se combinaron, qué papel desempeñaron las infraestructuras y qué enseñanzas puede extraer la ingeniería para afrontar futuros episodios extremos.

Un desastre resultado de múltiples vulnerabilidades

La vulnerabilidad que puso de manifiesto la DANA no obedeció a una única causa. Fue el resultado de la combinación de una elevada exposición de la población, de las actividades económicas y de las infraestructuras en zonas potencialmente inundables, de las características de las redes de drenaje y de transporte y de la extraordinaria magnitud de la avenida.

En comarcas como l’Horta Sud, el crecimiento urbano e industrial acumulado durante décadas ocupó parte de las llanuras naturales de inundación y de los cauces secos de las ramblas. Al mismo tiempo, la sustitución de superficies vegetadas por superficies impermeables favoreció una respuesta más rápida de la escorrentía y redujo la infiltración del agua.

A estas condiciones se sumaron ciertos elementos de las infraestructuras que pueden modificar el comportamiento del flujo durante una inundación. Algunos puentes con pilares situados en el cauce y determinados terraplenes de las vías de transporte pueden generar estrechamientos locales. Si además se acumulan escombros, vegetación u otros materiales arrastrados por el agua, la circulación de los caudales puede verse temporalmente dificultada.

La magnitud de los daños puede entenderse mediante el denominado «modelo del queso suizo», utilizado en la gestión de desastres. Su planteamiento parte de que los impactos más graves pueden producirse cuando varias debilidades o limitaciones coinciden en distintas capas de protección. Durante este episodio confluyeron factores territoriales e hidráulicos preexistentes con circunstancias propias de la emergencia.

Entre las condiciones previas estaba la existencia de cuencas de respuesta rápida, con capacidad hidráulica limitada, destinadas a episodios extraordinarios. La respuesta fue diferente en infraestructuras con mayor capacidad de regulación o de conducción, como el nuevo cauce del Turia o la presa de Forata en el río Magro. Durante la emergencia también intervinieron aspectos relacionados con la transmisión de información y la percepción del riesgo, incluidos los sistemas de alerta temprana y el conocimiento del peligro por parte de la población.

Todo ello coincidió con un episodio meteorológico excepcional. La DANA produjo precipitaciones de intensidad extraordinaria y se vio favorecida por temperaturas del Mediterráneo superiores a lo habitual para las condiciones atmosféricas del episodio. Además, el sistema de tormentas presentó un carácter muy estacionario, lo que permitió acumular precipitaciones históricas en determinados puntos. En Turís se registraron más de 185 l/m² en una hora y más de 770 l/m² en 24 horas. Los caudales generados superaron ampliamente los valores asociados a periodos de retorno convencionales.

Revisar los modelos de riesgo hidrológico

El episodio también ha puesto sobre la mesa algunas limitaciones conceptuales y metodológicas en la evaluación del riesgo hidrológico. Una de las cuestiones que merecen revisión es la premisa de la estacionariedad climática: la suposición de que las series estadísticas y los registros históricos permiten estimar adecuadamente la frecuencia e intensidad de los acontecimientos futuros.

La DANA plantea interrogantes sobre la capacidad de los periodos de retorno convencionales utilizados en las normativas para representar un clima cambiante, capaz de generar sistemas de tormentas estacionarias de severidad excepcional. También conviene mejorar la representación de aquellas situaciones en las que las precipitaciones extremas inciden sobre suelos previamente saturados por lluvias anteriores, ya que esta circunstancia puede contribuir a producir picos de caudal muy elevados.

Los modelos hidrológicos e hidráulicos deberían incorporar también, con mayor detalle, la geomorfología de los abanicos y de las llanuras aluviales mediterráneas. Muchas metodologías de evaluación del riesgo se han desarrollado tomando como referencia la dinámica de los grandes ríos. En un abanico aluvial, la configuración convexa del terreno puede hacer que el cauce pierda capacidad a medida que avanza, mientras que el agua desbordada puede desviarse hacia corrientes secundarias.

Las infraestructuras humanas añaden otra fuente de complejidad. Algunos modelos numéricos podrían no representar con suficiente detalle determinadas interacciones físicas, como la acumulación de vehículos, sedimentos, vegetación y escombros en puentes y pasos inferiores. Estos materiales pueden incrementar el calado y las fuerzas ejercidas sobre el entorno aguas arriba.

También existe margen para conectar mejor los datos disponibles con la gestión predictiva de emergencias en tiempo real. Una red avanzada de medición como el SAIH proporciona información de gran utilidad, que podría adquirir mayor valor operativo mediante su integración con modelos hidráulicos distribuidos capaces de transformar la precipitación en mapas dinámicos de inundación.

El análisis del riesgo debería extenderse, además, más allá de la seguridad estructural de cada componente considerado por separado. La electricidad, el agua, las telecomunicaciones y el transporte están estrechamente relacionados, de modo que el fallo de un sistema puede afectar a los demás. Los modelos deben profundizar en estos posibles efectos en cascada y en las interdependencias entre infraestructuras críticas, incluyendo los tiempos necesarios para la recuperación de los servicios.

Infraestructuras que protegen y estructuras que interactúan con el agua

No todas las infraestructuras cumplen la misma función en una inundación. Su comportamiento depende de su capacidad de evacuación, de su función de laminación de caudales y de la forma en que responden hidráulicamente a las características concretas de cada episodio.

El nuevo cauce del río Turia, conocido como Plan Sur, constituye un elemento relevante por su capacidad de conducción para interpretar la evolución de los caudales en el entorno de Valencia. También las presas de regulación y laminación, como Forata, pueden modificar temporalmente la evolución de los caudales aguas abajo. Para determinar cuál fue la contribución concreta de estas infraestructuras durante la DANA, es necesario analizar los caudales registrados, las condiciones de funcionamiento y los escenarios que se habrían producido sin dichas actuaciones.

Otros elementos pueden interactuar con el flujo y modificar localmente sus condiciones de circulación. En determinados puentes y pasos con varios pilares dentro del cauce, la acumulación de vegetación, sedimentos, vehículos u otros materiales arrastrados por la corriente puede reducir temporalmente la sección disponible y modificar los niveles de agua aguas arriba. La magnitud de este efecto depende del emplazamiento y requiere un análisis hidráulico específico.

Algo similar puede ocurrir con ciertos terraplenes de carreteras y de vías ferroviarias. Su comportamiento frente a caudales extraordinarios depende, entre otros factores, de la capacidad y la distribución de los elementos de drenaje transversal.

Esto aconseja revisar las soluciones existentes sin considerar si una determinada tipología es adecuada o inadecuada de forma general. En puentes y pasos de agua puede estudiarse, cuando sea técnicamente viable, la reducción de apoyos dentro del cauce, junto con la socavación y las acciones asociadas a sedimentos y materiales flotantes. En carreteras y ferrocarriles puede valorarse una mayor permeabilidad transversal mediante obras de drenaje, marcos o viaductos, especialmente cuando la configuración del terreno lo permita.

La ingeniería dispone, además, de soluciones que pueden combinarse entre sí. Entre ellas están las medidas de laminación en cabecera y aquellas que proporcionan mayor espacio para la circulación temporal del agua, como parques inundables periurbanos, corredores verdes de laminación y Sistemas Urbanos de Drenaje Sostenible (SUDS). Estas actuaciones pueden complementarse con criterios de diseño basados en el desempeño y con hipótesis de cálculo que contemplen posibles modificaciones en las condiciones climáticas.

También resulta útil estudiar qué ocurre cuando un evento supera las condiciones previstas en el diseño. El objetivo es identificar posibles modos de fallo y conservar determinadas funciones durante la emergencia.

Carreteras, ferrocarriles y puentes: analizar cada caso

Las infraestructuras de transporte pueden interactuar con el agua de distintas formas durante una inundación. Su efecto depende de su posición respecto a las líneas naturales de escorrentía, de la permeabilidad transversal, de la capacidad de las obras de drenaje y de las características de los caudales y de los materiales transportados. Por ello, su influencia debe analizarse de manera individual.

En algunos puentes, la presencia de varios pilares o apoyos en el cauce facilita que la vegetación, los sedimentos, los vehículos y otros materiales arrastrados por la corriente reduzcan temporalmente la sección transversal disponible. Los terraplenes de carreteras y ferrocarriles también pueden interceptar las líneas de escorrentía cuando sus elementos de drenaje transversal carecen de capacidad suficiente para caudales determinados.

Algunas infraestructuras de l’Horta Sud merecen un análisis específico. Entre ellas figuran determinados tramos de la red ferroviaria de cercanías, incluido el entorno de Paiporta, donde convendría estudiar conjuntamente los niveles de agua registrados, la capacidad de las obras de drenaje y las posibles obstrucciones durante el episodio.

También puede revisarse el comportamiento hidráulico de grandes infraestructuras viarias, como la V-31, conocida como Pista de Silla, y la CV-31, así como su relación con las vías naturales de desagüe del abanico aluvial. Las diferencias de configuración respecto de otras infraestructuras, como la CV-400 o la línea del AVE, pueden aportar información útil, aunque por sí solas no permiten establecer una relación causal con su comportamiento durante la DANA.

Otro caso que merece atención es el del Barranco de la Saleta y su relación con el tejido urbano de Aldaia. La evolución del agua durante un episodio extraordinario depende de la configuración del cauce, de las condiciones de drenaje y de las actuaciones existentes o previstas. Cualquier modificación debería basarse en una evaluación hidráulica conjunta de estas variables.

Los futuros rediseños y reconstrucciones deberían evaluar la permeabilidad y el comportamiento hidráulico de estas infraestructuras. Entre las medidas posibles figuran reducir, cuando sea viable, el número de apoyos dentro del cauce, estudiar la socavación y las acciones asociadas a materiales flotantes y mejorar la permeabilidad transversal de carreteras y ferrocarriles mediante obras de drenaje, marcos o viaductos. La solución debe adaptarse a las características hidráulicas y territoriales de cada emplazamiento.

Reconstruir no significa simplemente reponer

La reconstrucción exige distinguir entre la respuesta asistencial y la reparación de los servicios afectados, por una parte, y la revisión de las condiciones que contribuyeron al riesgo, por otra. Durante la emergencia se realizó un esfuerzo importante para recuperar la conectividad viaria y ferroviaria y restablecer las redes de abastecimiento, de agua potable y de saneamiento.

La reducción de vulnerabilidades requiere, sin embargo, analizar cada actuación y comprobar hasta qué punto incorpora las lecciones del episodio. Una cuestión relevante es determinar si las obras de reposición conservan las características de las infraestructuras anteriores o incorporan modificaciones destinadas a mejorar su comportamiento ante futuros episodios.

Reponer una infraestructura dañada permite atender una necesidad inmediata, pero no implica necesariamente que se hayan revisado las condiciones territoriales, hidráulicas o de diseño que deberían tenerse en cuenta ante otros acontecimientos. La reconstrucción también ofrece la oportunidad de revisar las soluciones existentes cuando los estudios técnicos así lo aconsejen.

Entre las actuaciones que podrían requerir atención específica figuran las medidas de laminación y de defensa en la cuenca del Barranco del Poyo y en otras zonas afectadas, así como las soluciones provisionales adoptadas en carreteras, puentes y cauces. Su adecuación dependerá de las características de cada actuación y de los plazos previstos para las soluciones definitivas. También conviene analizar cómo respondería el conjunto de infraestructuras ante un nuevo episodio, antes de que concluyan las actuaciones previstas.

La reducción de las vulnerabilidades identificadas puede requerir una coordinación más estrecha entre administraciones y organismos responsables, así como de equipos técnicos capaces de estudiar conjuntamente las dimensiones hidráulicas, territoriales, urbanas e infraestructurales.

Entre los aspectos susceptibles de revisión se encuentran los criterios de cálculo ante posibles cambios climáticos, las normas de ocupación de zonas potencialmente inundables y la localización de usos especialmente sensibles. También puede estudiarse la implantación de infraestructuras verdes y azules, como parques inundables y sistemas de drenaje sostenible, adaptadas a las características específicas del territorio.

El objetivo no debería limitarse a recuperar el funcionamiento previo de las zonas afectadas. También debe estudiarse qué modificaciones pueden reducir de manera razonable la exposición y mejorar la capacidad de respuesta ante futuros episodios. El alcance de esas modificaciones debe establecerse mediante estudios técnicos específicos para cada territorio y cada infraestructura.

Diseñar pensando en un clima que cambia

No todas las infraestructuras están todavía diseñadas de forma sistemática considerando la posible no estacionariedad de las condiciones climáticas futuras. Muchos códigos y regulaciones de ingeniería se han apoyado históricamente en series de datos y registros del pasado para definir las acciones de diseño, bajo la hipótesis de que sus características estadísticas permanecerían relativamente estables.

La evolución observada y proyectada del clima plantea la necesidad de revisar hasta qué punto ese supuesto sigue siendo adecuado para determinados tipos de infraestructura. Además, muchas obras tienen vidas útiles de varias décadas, por lo que las condiciones a las que estarán expuestas pueden diferir de las consideradas durante su diseño.

La adaptación no afecta únicamente a los valores de cálculo. También conviene estudiar cómo responderán las infraestructuras ante combinaciones de fenómenos extremos y cómo se recuperarán los servicios tras un episodio severo. Tradicionalmente se ha prestado mucha atención a la seguridad de los elementos individuales, pero la interdependencia entre electricidad, agua, telecomunicaciones y transporte hace necesario estudiar también los posibles efectos en cadena.

Una vía de adaptación consiste en avanzar hacia criterios de Diseño Basado en el Desempeño (PBD) y ampliar el uso de la modelización probabilística del riesgo. Esto incluye actualizar periódicamente las curvas de intensidad-duración-frecuencia (IDF) y los mapas de carga, incorporando información climática y distintos escenarios futuros junto con los registros históricos.

Las hipótesis de diseño también pueden revisarse cuando nuevos datos indiquen cambios relevantes en las condiciones de exposición. El reto consiste en trasladar los avances del conocimiento climático a las normas técnicas y a la planificación territorial, manteniendo márgenes adecuados de incertidumbre.

En infraestructuras con una vida útil prolongada puede ser especialmente útil incorporar criterios que permitan adaptar su funcionamiento o sus características si las condiciones futuras difieren de las previstas inicialmente. Así, el diseño no se orientaría únicamente a la resistencia frente a determinados episodios, sino también a la conservación de las funciones y los servicios durante y después de situaciones extremas.

«Devolverle espacio al agua»

«Devolverle espacio al agua», o «dar espacio al río», significa permitir que el agua disponga de lugares por los que pueda circular, extenderse o almacenarse temporalmente durante una avenida, en lugar de intentar contenerla siempre dentro de un cauce o mediante infraestructuras rígidas.

La idea consiste en recuperar, cuando las condiciones territoriales lo permitan, parte del espacio que históricamente ocupaba el agua y que la urbanización ha ido reduciendo. En la práctica, esto puede traducirse en recuperar zonas inundables, ampliar determinados espacios fluviales, crear parques inundables o mejorar la permeabilidad del suelo mediante Soluciones Basadas en la Naturaleza e infraestructuras verdes y azules.

Estas medidas pueden almacenar temporalmente parte del agua y reducir la presión sobre otros elementos del sistema, aunque su eficacia depende de las características concretas del territorio y de cada episodio.

Dar espacio al agua no implica descartar las infraestructuras tradicionales. Estas siguen siendo necesarias en determinados lugares. La gestión del riesgo puede combinar obras de protección con espacios destinados a la circulación y al almacenamiento temporal del agua, además de una ordenación territorial que tenga en cuenta las zonas potencialmente inundables. La combinación adecuada debe determinarse en cada territorio mediante los estudios correspondientes.

Una estrategia integrada para futuras DANAs

La reducción del impacto de una futura DANA requiere un enfoque integrado, ya que ninguna solución aislada puede mitigar por sí sola todos los efectos de una avenida extraordinaria.

Una línea de actuación consiste en mejorar la laminación y retención de caudales en las cuencas, combinando, cuando sea adecuado, presas o balsas con soluciones basadas en la naturaleza, como parques inundables, corredores verdes y Sistemas Urbanos de Drenaje Sostenible. El objetivo es reducir los picos de avenida y proporcionar más espacio para la circulación y el almacenamiento temporal del agua.

También debe revisarse la permeabilidad hidráulica de carreteras, ferrocarriles y puentes, mejorar las obras de drenaje y reducir los obstáculos al flujo cuando sea viable. Junto con las actuaciones físicas, conviene reforzar los sistemas de información y alerta, integrando los datos del SAIH con modelos capaces de proporcionar información hidráulica útil en caso de emergencia. Estos sistemas deben coordinarse con los planes de actuación y con la formación de la población.

Una confianza excesiva en una única infraestructura de protección —presas, muros o encauzamientos— puede generar una falsa sensación de seguridad si se asume que basta para garantizar la protección ante cualquier avenida. Algo parecido ocurre cuando se mantienen o se amplían usos urbanos en zonas inundables debido a la presencia de una obra defensiva, sin considerar que el episodio puede superar las condiciones para las que fue diseñada.

También merece atención la reconstrucción de una infraestructura exactamente con la misma configuración que tenía antes de resultar dañada, sin comprobar si esa solución sigue siendo adecuada. Actuaciones puntuales, como limpiar un cauce, ampliar un colector o mejorar un paso de drenaje, pueden resolver problemas concretos, pero no constituyen por sí mismas una respuesta suficiente frente a una avenida de gran magnitud si no se estudia el funcionamiento del sistema completo.

¿Qué habría cambiado si la DANA se repitiera hoy?

Si actualmente se produjera un episodio pluviométrico de magnitud similar, algunos sistemas de seguimiento y alerta podrían estar en mejores condiciones para detectar y comunicar determinadas situaciones. El SAIH, los avisos de Protección Civil y herramientas como ES-Alert podrían facilitar una transmisión más rápida de la información disponible. La experiencia de 2024 también puede haber modificado la percepción del riesgo tanto entre la población como en las administraciones.

Una alerta más temprana, sin embargo, no garantiza por sí misma resultados completamente distintos. Su eficacia dependería de la anticipación disponible, la precisión de la información, el tiempo de reacción y la capacidad de la población y de los servicios de emergencia para actuar. La mejora de estos sistemas puede reducir determinados riesgos, pero no permite garantizar la prevención de todas las consecuencias de un episodio de magnitud semejante.

La configuración física del territorio es otra cuestión. En el tiempo transcurrido desde la DANA, difícilmente habrían podido cambiar de manera sustancial las condiciones territoriales que determinan el comportamiento de una inundación. Las grandes actuaciones hidráulicas, las modificaciones de infraestructuras y los cambios en la ordenación urbana requieren años de estudios, proyectos, tramitación y ejecución.

Aunque algunas actuaciones ya están en marcha, la llanura de inundación de l’Horta Sud mantiene una elevada exposición y determinadas soluciones siguen siendo provisionales o aún están en ejecución.

La diferencia entre una repetición del episodio de hoy y la situación de 2024 podría encontrarse, así, en una mayor capacidad de anticipación y respuesta, mientras que buena parte de las condiciones físicas seguiría siendo similar. Reducir esa vulnerabilidad exige actuaciones que necesitan más tiempo y que deben apoyarse en el conocimiento técnico del territorio, de las infraestructuras y del comportamiento hidráulico de episodios extremos.

Licencia de Creative Commons
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Seis secretos de la perforación horizontal: la tecnología invisible que construye el mundo bajo tus pies

Figura 1. Esquema de Perforación Horizontal Dirigida

Todos conocemos la estampa: una calle principal cortada, el ensordecedor ruido de la maquinaria, el tráfico desviado durante semanas y zanjas abiertas que suponen un obstáculo constante. Estas son las molestias habituales de las obras urbanas tradicionales, una realidad que asumimos como necesaria para mantener y ampliar las infraestructuras que nos prestan servicio. Sin embargo, bajo nuestros pies se está produciendo una revolución silenciosa. Existe una forma de instalar tuberías esenciales para el agua, el gas, la electricidad o las telecomunicaciones sin que apenas nos demos cuenta: las «tecnologías sin zanja».

Una de las más revolucionarias es la Perforación Horizontal Dirigida (PHD). Aunque su trabajo es invisible, su impacto es monumental. Este artículo revela seis aspectos sorprendentes sobre el funcionamiento de esta tecnología que está transformando el subsuelo de nuestras ciudades de manera más inteligente, rápida y respetuosa con el medio ambiente.

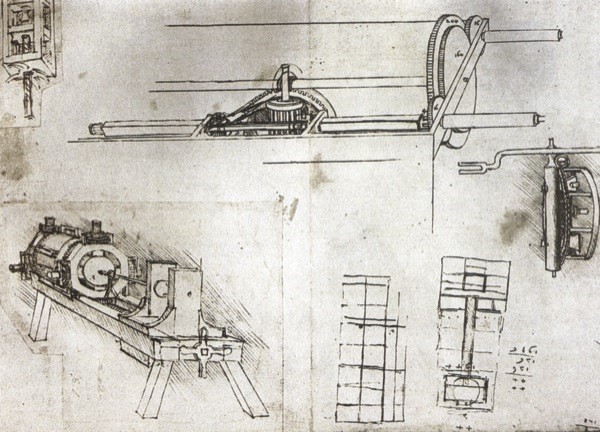
Figura 2. Máquina de perforación horizontal ideada por Leonardo da Vinci, antes de 1495. Fuente: http://trenchless-australasia.com/

1. Una idea renacentista: sus orígenes se remontan a Leonardo da Vinci.

Cuando pensamos en una tecnología tan sofisticada, capaz de perforar kilómetros bajo tierra con precisión centimétrica, la asociamos instintivamente al siglo XXI. La realidad es mucho más sorprendente. La idea conceptual de una máquina de perforación horizontal fue concebida nada menos que por Leonardo da Vinci antes de 1495. Aunque tuvieron que pasar casi cinco siglos para que la tecnología madurara, la primera instalación moderna de PHD con una tubería de acero se llevó a cabo en 1971 para cruzar el río Pájaro, en California.

Es fascinante reflexionar sobre cómo una visión renacentista sentó las bases de una de las técnicas de construcción más avanzadas de nuestro tiempo. Este largo camino de innovación demuestra que a menudo las grandes ideas necesitan siglos para encontrar las herramientas adecuadas para hacerse realidad, conectando el genio de un artista del pasado con las necesidades de la ingeniería del futuro.

2. No se trata solo de evitar zanjas, sino de salvar la vida útil de nuestras ciudades.

El principal beneficio que se asocia a la PHD es la comodidad: evitar el caos de las zanjas abiertas. Sin embargo, su verdadero impacto es mucho más profundo y estratégico. El método tradicional de abrir y cerrar zanjas tiene un coste oculto devastador para nuestras infraestructuras. Según los expertos, la simple apertura de una zanja puede reducir la vida útil de un pavimento en un 30 %. Esto significa que las calles que deberían durar décadas se deterioran prematuramente, lo que obliga a realizar reparaciones costosas y constantes.

Por tanto, el beneficio de la PHD va mucho más allá de la simple conveniencia. Se trata de una decisión económica y ecológica fundamental. Al eliminar la necesidad de excavar, no solo se reducen los plazos de ejecución, el impacto ambiental y las restricciones de tráfico, sino que también se preserva la integridad de la infraestructura urbana existente. En última instancia, esto reduce los costes finales de la obra y protege una de las inversiones públicas más importantes: nuestras calles y carreteras.

3. No se perfora a ciegas, sino que se «navega» bajo tierra con precisión centimétrica.

Una de las ideas erróneas más comunes sobre la perforación horizontal dirigida (PHD) es imaginarla como un proceso de perforación «a ciegas». Nada más lejos de la realidad. La cabeza de perforación es, básicamente, un vehículo teledirigido que se «navega» bajo tierra con una precisión asombrosa. La trayectoria se controla en todo momento mediante sistemas de navegación avanzados, lo que permite alcanzar grandes longitudes con una precisión centimétrica.

Existen tres tipos principales de sistemas para guiar la perforación:

  • «Walk-Over»: similar a un detector de metales muy avanzado, un operario camina por la superficie siguiendo la trayectoria de la cabeza perforadora en tiempo real.
  • «Wire-Line»: un cable en el interior de la sarta de perforación transmite la información de posición.
  • «Gyro Compass»: un sistema giroscópico, similar al utilizado en aeronáutica, permite una navegación autónoma sin necesidad de acceder a la superficie.
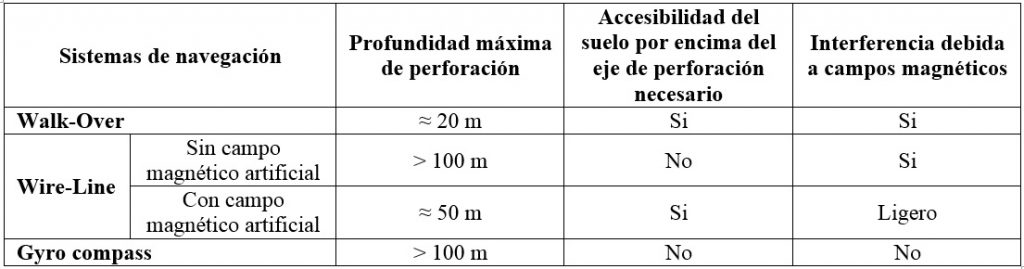
Tabla. Diferentes procedimientos de navegación de PHD (IbSTT, 2013).

Esta precisión no es un lujo, sino una necesidad crítica. No solo garantiza que la perforación llegue al punto de salida exacto, sino que también es fundamental para evitar dañar la maraña de servicios soterrados existente (cables de fibra óptica, tuberías de gas y conducciones de agua). Un error podría acarrear «desorbitados costes legales por daños a terceros», convirtiendo una obra eficiente en un desastre económico y de seguridad.

4. El héroe anónimo: El fluido de perforación es mucho más que «lodo».

En cualquier operación de PHD se puede observar un fluido espeso, que a menudo se denomina «mud» o lodo, que circula constantemente. Podría parecer un simple subproducto, pero en realidad es uno de los componentes con mayor ingeniería de todo el proceso y el verdadero héroe anónimo de la operación, ya que cumple cinco funciones cruciales e irremplazables. Su composición se diseña específicamente para la geología del terreno que se va a atravesar y cumple cinco funciones cruciales e irremplazables:

  • Refrigerar las herramientas de corte, que giran a gran velocidad y generan una intensa fricción.
  • Ayudar en el corte del terreno gracias a la alta presión con la que se inyecta (efecto hidrojet).
  • Transportar los detritos (el material excavado) fuera del túnel y mantenerlo limpio.
  • Lubricar tanto la sarta de perforación como la tubería final durante su instalación.
  • Contener y mantener estables las paredes de la perforación, creando una especie de «revestimiento» temporal que evita derrumbes.

Sin este fluido multifuncional, la técnica sería inviable. Garantiza la estabilidad del túnel, la eficiencia del corte y el éxito de la instalación de la tubería.

Figura 3. Escariador. Imágen de Catalana de Perforacions

5. La paradoja de la rapidez: el éxito depende de una planificación meticulosa.

Una de las grandes ventajas de la PHD es su rapidez de ejecución en comparación con los métodos tradicionales. Sin embargo, esta rapidez en la fase de obra es el resultado de una fase de preparación extraordinariamente exhaustiva. En el sector se utiliza una proporción muy reveladora: «1 día de trabajo, 2 de planificación». El éxito no se improvisa, se diseña.

Antes de que entre en funcionamiento la primera máquina, es imprescindible valorar la viabilidad del proyecto mediante estudios previos. Estos incluyen análisis topográficos detallados y, fundamentalmente, estudios geológicos exhaustivos para conocer a la perfección el subsuelo. Estos estudios, realizados por geólogos expertos en la técnica PHD, pueden incluir perforaciones de investigación, prospecciones geofísicas (como el georradar para detectar servicios enterrados) y pruebas de laboratorio de los materiales del terreno. El objetivo es claro: reducir los riesgos de construcción al mínimo y anticiparse a cualquier obstáculo o cambio en el terreno antes de empezar a perforar. Esta fase de preparación es la que garantiza que la «navegación» subterránea sea un éxito y no un desastre, y evita precisamente los «desorbitados costes legales» que se producirían al dañar servicios existentes.

6. Mucho más que tuberías: creando tomas de agua que protegen los ecosistemas marinos.

Si bien la PHD es una aliada clave en entornos urbanos, algunas de sus aplicaciones más innovadoras y con mayor impacto se encuentran en la protección de ecosistemas sensibles. Dos ejemplos de ello son las tecnologías «APPROACH» y «NEODREN®», que utilizan la PHD como herramienta de ingeniería medioambiental.

  • APPROACH permite realizar conexiones tierra-mar, como emisarios o tomas de agua, sin dañar la zona intermareal y submarina vulnerable. La perforación se realiza desde tierra firme y sale directamente en el punto deseado del fondo marino, evitando así cualquier tipo de excavación en la costa o en el lecho marino.
  • NEODREN® es un sistema revolucionario de captación de agua marina. Su genialidad consiste en que, en lugar de una simple toma de agua marina, convierte el propio subsuelo marino en una planta de filtración natural. Se instalan múltiples drenes horizontales desde la costa hasta una capa permeable bajo el lecho marino. Estos drenes funcionan como un pozo de alto volumen que extrae agua de mar después de que esta se haya filtrado lentamente a través de la arena y las rocas, «consiguiéndose un agua de alta calidad, sin turbidez y de caudal constante», ideal para plantas desalinizadoras. Este método elimina por completo la necesidad de realizar excavaciones en el fondo marino.
Figura 4. Neodren®. https://www.catalanadeperforacions.com/es/soluciones/sistema-neodren/neodren-captacion-de-agua-marina/

El impacto ecológico de estas aplicaciones es enorme, tal y como lo resumen los expertos, al ser una técnica subterránea, se evita trabajar en la zona marítima, que es de difícil maniobra y siempre está expuesta a daños causados por temporales, al mismo tiempo que se protegen zonas de especial valor ecológico, como las praderas de posidonia. Así, la PHD trasciende su papel como técnica de construcción para convertirse en una herramienta que permite desarrollar infraestructuras críticas en perfecta armonía con el entorno y proteger los ecosistemas que antes se sacrificaban en nombre del progreso.

Conclusión: la próxima frontera de la construcción ya está aquí.

La perforación horizontal dirigida es mucho más que un método ingenioso para evitar zanjas. Se trata de una disciplina de alta tecnología con una historia sorprendente, una precisión casi quirúrgica y aplicaciones innovadoras que están redefiniendo la construcción moderna. Nos muestra que el futuro de la infraestructura no radica en dominar la superficie, sino en trabajar de manera inteligente y respetuosa con el entorno que se encuentra debajo, lo que hace que nuestras ciudades y costas sean más eficientes, resilientes y sostenibles.

La próxima vez que camines por una calle sin obras ni atascos o disfrutes de una playa virgen, ¿te preguntarás qué maravillas de la ingeniería se están construyendo silenciosamente bajo tus pies?

A continuación, dejo un audio donde se habla del PHD.

También os dejo este vídeo, donde se resumen conceptos importantes. No obstante, en este blog encontrarás muchos más vídeos y artículos sobre este tema de tanto interés.

Referencias:

Allouche, E., Ariaratnam, S., and Lueke, J. (2000). Horizontal Directional Drilling: Profile of an Emerging Industry. Journal of Construction Engineering and Management, Volume 126, No. 1, pp. 68–76.

Ariaratnam, S. T., and Allouche, E. N. (2000). Suggested practices for installations using horizontal directional drilling. Practice Periodical on Structural Design and Construction, Volume 5, No. 4, pp. 142-149.

Ariaratnam, S. T., and Proszek, J. (2006). Legal consequences of damages to underground facilities by horizontal directional drilling. Journal of Professional Issues in Engineering Education and Practice, Volume 132, No. 4, pp. 342-354.

IbSTT Asociación Ibérica de Tecnología SIN Zanja (2013). Manual de Tecnologías Sin Zanja.

Jaganathan, A. P., Shah, J. N., Allouche, E. N., Kieba, M., and Ziolkowski, C. J. (2011). Modeling of an obstacle detection sensor for horizontal directional drilling (HDD) operations. Automation in Construction, Volume 20, No. 8, pp. 1079-1086.

Lubrecht, M. D. (2012). Horizontal directional drilling: A green and sustainable technology for site remediation. Environmental Science & Technology, Volume 46, No. 5, pp. 2484-2489.

Yepes, V. (2014). Maquinaria para sondeos y perforaciones. Apuntes de la Universitat Politècnica de València, Ref. 209. Valencia, 89 pp.

Yepes, V. (2015). Aspectos generales de la perforación horizontal dirigida. Curso de Postgrado Especialista en Tecnologías Sin Zanja, Ref. M7-2, 10 pp.

Licencia de Creative Commons
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Microtúneles: Tecnología sin zanja para la construcción subterránea

Figura 1. Microtúnel.https://purewater-int.com/services/microtunneling/

La ingeniería civil ha desarrollado tecnologías avanzadas que permiten la instalación y el mantenimiento de infraestructuras subterráneas sin afectar significativamente a la superficie. Una de estas tecnologías, particularmente útil en áreas urbanas y entornos sensibles, es la de los microtúneles.

En este artículo, exploraremos los aspectos principales de los microtúneles, sus ventajas y limitaciones, los distintos tipos de escudos y los métodos de revestimiento, como el uso de dovelas y la hinca de tubería, que aseguran la estabilidad de los túneles.

1. ¿Qué son los microtúneles?

Los microtúneles son un tipo específico de tecnología sin zanja diseñada para instalar tuberías y conductos subterráneos a través de un proceso de perforación y revestimiento controlado, sin requerir excavaciones abiertas en la superficie. Estos túneles de pequeño diámetro suelen utilizarse para instalar colectores, redes de agua y sistemas de alcantarillado. A diferencia de otras técnicas de perforación, los microtúneles ofrecen mayor precisión y estabilidad estructural, ya que se utilizan tuneladoras y sistemas de guiado avanzados.

Ventajas de los microtúneles

  • Impacto mínimo en la superficie: Como no es necesario abrir zanjas, los microtúneles reducen las interrupciones en el tráfico y minimizan los daños en la infraestructura existente.
  • Menor impacto ambiental: Este método evita la remoción de grandes cantidades de tierra y reduce los desechos de la construcción, por lo que es una opción más ecológica.
  • Ideal para áreas de difícil acceso: Al requerir solo pozos de entrada y salida, los microtúneles son ideales para trabajos en áreas urbanas densamente pobladas o bajo infraestructuras ya existentes.

Limitaciones de los microtúneles

  • Costos iniciales elevados: La maquinaria y planificación requerida pueden aumentar los costos, especialmente en terrenos sencillos donde una excavación tradicional sería suficiente.
  • Necesidad de estudios geotécnicos detallados: Para asegurar el éxito del proyecto, es necesario un análisis exhaustivo del tipo de suelo, así como un diseño específico para el trazado y la maquinaria a emplear.

2. Maquinaria y equipos utilizados en la perforación de microtúneles

La construcción de microtúneles requiere diferentes tipos de escudos, que son dispositivos que protegen el frente de excavación y facilitan la extracción de material. El tipo de escudo elegido depende de las características del terreno y de las especificaciones del proyecto.

Tuneladoras de escudo abierto

Los escudos abiertos son los más básicos y se utilizan en terrenos cohesivos y por encima del nivel freático. Su diseño permite que el personal trabaje dentro del escudo y retire el material excavado mediante cintas transportadoras o vagonetas. Sin embargo, su principal limitación es que no pueden prevenir derrumbes, lo que los hace adecuados solo para suelos estables. Existen versiones que utilizan aire presurizado para estabilizar el entorno en algunas condiciones.

Tuneladoras de escudo cerrado

Las tuneladoras de escudo cerrado son las máquinas principales utilizadas en los microtúneles. Estos equipos están diseñados para evitar derrumbes y permiten un control preciso sobre la extracción del material excavado. Existen dos tipos principales de tuneladoras de escudo cerrado:

  • Tuneladora EPB (Earth Pressure Balance): Equilibra la presión en el frente usando el propio material excavado, lo cual es especialmente útil en terrenos arcillosos. Además, utiliza espumas y polímeros para estabilizar el suelo.
  • Tuneladora hidroescudo: Este tipo de tuneladora utiliza lodos para estabilizar el frente de excavación, lo que resulta especialmente útil en suelos arenosos o bajo el nivel freático.

Ambos tipos de escudos permiten extraer el material en seco o húmedo, asegurando una operación segura y eficiente en diversas condiciones geológicas.

Figura 2. Tuneladora EPB. https://www.gypsum.in/microtunneling/

3. Métodos de revestimiento en microtúneles

Un aspecto importante en la construcción de microtúneles es el revestimiento, que garantiza la estabilidad y durabilidad del túnel, especialmente en terrenos inestables. Existen dos métodos principales de revestimiento: el método de dovelas y el método de hinca de tubería.

Revestimiento con dovelas

Este método consiste en el uso de dovelas, secciones de anillo prefabricadas, que se ensamblan en el interior del túnel a medida que avanza la tuneladora. El procedimiento implica montar las dovelas dentro de la máquina y posteriormente inyectar mortero en el trasdós para garantizar la estabilidad del revestimiento y evitar filtraciones. Este método permite construir túneles con radios de curvatura pequeños, adaptándose a trazados complejos y de gran diámetro.

Revestimiento con hinca de tubería

El revestimiento con hinca de tubería es ideal para túneles de menor diámetro y consiste en empujar tramos de tubería prefabricada desde el pozo de ataque hasta el pozo de salida. Este proceso puede incorporar estaciones intermedias para longitudes extensas, y utiliza bentonita como lubricante para reducir la fricción durante la hinca. La principal ventaja de este método es que no requiere que el personal opere dentro de la tuneladora y facilita la alineación precisa gracias al sistema de guiado continuo.

Ambos métodos de revestimiento cumplen la función de asegurar la estabilidad y el sellado del túnel, aunque su selección dependerá de las características específicas del proyecto.

4. Planificación y ejecución de un proyecto de microtúnel

Para llevar a cabo un proyecto de microtúnel, es fundamental una planificación detallada que incluya:

  • Estudios geotécnicos: Analizar el tipo de suelo es esencial para definir el equipo y las técnicas de excavación adecuadas, especialmente en terrenos variables o inestables.
  • Selección de tuneladora y herramientas de corte: La tuneladora debe ser seleccionada en función de las condiciones del suelo, y equipada con herramientas de corte específicas.
  • Diseño del pozo de ataque: Los pozos de entrada y salida deben ser diseñados para facilitar el montaje y operación de la tuneladora.
  • Sistema de guiado: Un sistema de guiado, como un teodolito láser motorizado, asegura que la perforación siga el trazado previsto, evitando desviaciones que podrían afectar la estructura del túnel.

5. Caso de estudio: El colector de Valdemarín

Un ejemplo destacado de aplicación de los microtúneles es el proyecto del colector de Valdemarín, en el que se utilizó una tuneladora EPB con dovelas para construir un colector de aguas en un terreno arenoso y de alta abrasividad. El colector, con un diámetro nominal de 2760 mm, fue diseñado para superar el reto de excavar bajo un nivel freático considerable y con una geometría compleja, incluyendo curvas de pequeño radio. Gracias a la tecnología de microtúnel, fue posible instalar el colector, minimizando el impacto en el entorno urbano y controlando el proceso de excavación en un suelo particularmente desafiante.

Conclusión

Los microtúneles son una solución avanzada para la construcción subterránea, especialmente útil en entornos urbanos densos y ambientalmente sensibles. Con diversas opciones de escudos (abiertos y cerrados) y métodos de revestimiento, como las dovelas y la hinca de tuberías, esta tecnología proporciona flexibilidad y precisión en una amplia gama de condiciones geológicas. La implementación de microtúneles sigue siendo una herramienta clave para el desarrollo de infraestructuras subterráneas sostenibles, ya que minimiza el impacto en la superficie y optimiza el proceso constructivo.

Os dejo algunos vídeos para ilustrar esta técnica constructiva.

Referencias:

FRENCH SOCIETY FOR TRENCHLESS TECHNOLOGY (FSTT). Microtunneling and Horizontal Drilling: Recommendations. John Wiley & Sons, 2010.

YEPES, V. (2014). Maquinaria para sondeos y perforaciones. Apuntes de la Universitat Politècnica de València, Ref. 209. Valencia, 89 pp.

YEPES, V. (2020). Procedimientos de construcción de cimentaciones y estructuras de contención. Colección Manual de Referencia, 2ª edición. Editorial Universitat Politècnica de València, 480 pp. Ref. 328. ISBN: 978-84-9048-903-1.

Licencia de Creative Commons
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Maquinaria y procedimientos de construcción: Problemas resueltos

Os presento el libro que he publicado sobre maquinaria y procedimientos de construcción. Se trata de una completa colección de 300 problemas resueltos, abarcando aspectos relacionados con la maquinaria, medios auxiliares y procedimientos de construcción. Su contenido se enfoca en la mecanización de las obras, costos, disponibilidad, fiabilidad y mantenimiento de equipos, estudio del trabajo, producción de maquinaria, sondeos y perforaciones, técnicas de mejora del terreno, control y abatimiento del nivel freático, movimiento de tierras, equipos de dragado, explosivos y voladuras, excavación de túneles, instalaciones de tratamiento de áridos, compactación de suelos, ejecución de firmes, maquinaria auxiliar como bombas, compresores o ventiladores, cables y equipos de elevación, cimentaciones y vaciados, encofrados y cimbras, fabricación y puesta en obra del hormigón, organización y planificación de obras.

Es un libro, por tanto, muy enfocado a los ámbitos de la ingeniería de la construcción, tanto en el ámbito de la edificación, de la minería o de la ingeniería civil. Además, se incluyen 27 nomogramas originales y 19 apéndices para apoyar tanto a estudiantes de ingeniería o arquitectura, como a profesionales que enfrentan desafíos similares en su práctica diaria en obra o proyecto. La colección se complementa con un listado de referencias bibliográficas que respaldan los aspectos teóricos y prácticos abordados en los problemas. Estos problemas son similares a los tratados durante las clases de resolución de casos prácticos en la asignatura de Procedimientos de Construcción del Grado en Ingeniería Civil de la Universitat Politècnica de València (España). Por tanto, el libro resulta adecuado tanto para estudiantes de grado como para cursos de máster relacionados con la ingeniería civil y la edificación.

El libro tiene 562 páginas. Este libro lo podéis conseguir en la propia Universitat Politècnica de València o bien directamente por internet en esta dirección: https://www.lalibreria.upv.es/portalEd/UpvGEStore/products/p_376-7-1

Sobre el autor: Víctor Yepes Piqueras. Doctor Ingeniero de Caminos, Canales y Puertos. Catedrático de Universidad del Departamento de Ingeniería de la Construcción y Proyectos de Ingeniería Civil de la Universitat Politècnica de València. Número 1 de su promoción, ha desarrollado su vida profesional en empresas constructoras, en el sector público y en el ámbito universitario. Ha sido director académico del Máster Universitario en Ingeniería del Hormigón (acreditado con el sello EUR-ACE®), investigador del Instituto de Ciencia y Tecnología del Hormigón (ICITECH) y profesor visitante en la Pontificia Universidad Católica de Chile. Imparte docencia en asignaturas de grado y posgrado relacionadas con procedimientos de construcción y gestión de obras, calidad e innovación, modelos predictivos y optimización en la ingeniería. Sus líneas de investigación actuales se centran en la optimización multiobjetivo, la sostenibilidad y el análisis de ciclo de vida de puentes y estructuras de hormigón.

Referencia:

YEPES, V. (2023). Maquinaria y procedimientos de construcción. Problemas resueltos. Colección Académica. Editorial Universitat Politècnica de València, 562 pp. Ref. 376. ISBN 978-84-1396-174-3

A continuación os paso las primeras páginas del libro, con el índice, para hacerse una idea del contenido desarrollado.

Pincha aquí para descargar

Un estudio de la UPV permite abaratar costes y reducir el impacto medioambiental en la construcción de túneles subterráneos

Figura 1. Marcos prefabricados en Vilaseca. Cortesía de ANDECE.

Un estudio realizado por investigadores de la Universitat Politècnica de València (UPV), pertenecientes al Instituto de Ciencia y Tecnología del Hormigón (ICITECH), ofrece una alternativa más económica y sostenible para la construcción con marcos prefabricados de hormigón de infraestructuras de transporte, como túneles subterráneos, edificios y otras estructuras. Sus resultados han sido publicados en la revista Materials.

En su trabajo, enmarcado dentro del proyecto Hydelife, han desarrollado diferentes algoritmos cuya aplicación permite ahorros económicos de hasta un 24% en el coste final de la estructura, disminuyendo los costes asociados con la producción y el transporte de materiales.

Además, según las estimaciones que ha realizado el equipo del ICITECH-UPV, permitiría optimizar el uso de materiales en la estructura y reducir alrededor de un 30% de las emisiones de CO₂ asociadas a la construcción.

“Pensemos una obra lineal donde tengamos, por ejemplo, 1000 metros de un túnel subterráneo que se pueda ejecutar con marcos prefabricados. Además del ahorro económico, en nuestro trabajo, estimamos que la reducción de 1 euro en el coste final de un marco de hormigón armado es equivalente a evitar la emisión de cerca de 2 kg de CO₂”, destaca Víctor Yepes, investigador del Instituto ICITECH de la Universitat Politècnica de València.

Así, este estudio presenta una alternativa sostenible y eficiente en términos de recursos para los marcos tradicionales de hormigón armado in situ.

“Nuestro objetivo era ampliar el conocimiento sobre la tipología estructural de marcos prefabricados articulados de hormigón y su empleo como sustituto de los marcos tradicionales de hormigón armado colado in situ. Y los resultados que hemos obtenido constatan su enorme potencial para grandes infraestructuras. El estudio es de especial interés para ámbitos como la ingeniería civil y arquitectura y, sobre todo, para las empresas de prefabricados de hormigón”, concluye Víctor Yepes.

Referencia:

RUIZ-VÉLEZ, A.; ALCALÁ, J.; YEPES, V. (2023). Optimal design of sustainable reinforced concrete precast hinged frames. Materials, 16(1):204. DOI:10.3390/ma16010204.

Os paso a continuación la repercusión de esta noticia en algunos medios de prensa.

Marcos prefabricados de hormigón para la construcción, una opción más barata y sostenible

Algoritmos para abaratar costes y reducir el impacto medioambiental al usar marcos prefabricados de hormigón en la construcción

https://24noticias.org/marcos-prefabricados-de-hormigon-alternativa-para-la-construccion/

https://www.levante-emv.com/sostenibilitat/2023/05/25/estudi-upv-revela-com-reduir-87816604.html

Algorithms for cleaner and cheaper construction of underground tunnels

https://www.upv.es/noticias-upv/noticia-14122-mas-sostenible-es.html

https://aplicat.upv.es/exploraupv/ficha-prensa/noticia/14122

https://www.cope.es/actualidad/sociedad/noticias/marcos-prefabricados-hormigon-para-construccion-una-opcion-mas-barata-sostenible-20230521_2719911

https://valenciaplaza.com/marcos-prefabricados-hormigon-construccion-opcion-mas-barata-sostenible

https://noticiasdelaciencia.com/art/46721/algoritmos-para-una-construccion-mas-limpia-y-mas-barata-de-tuneles-subterraneos