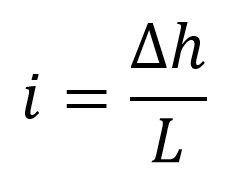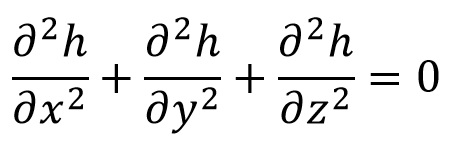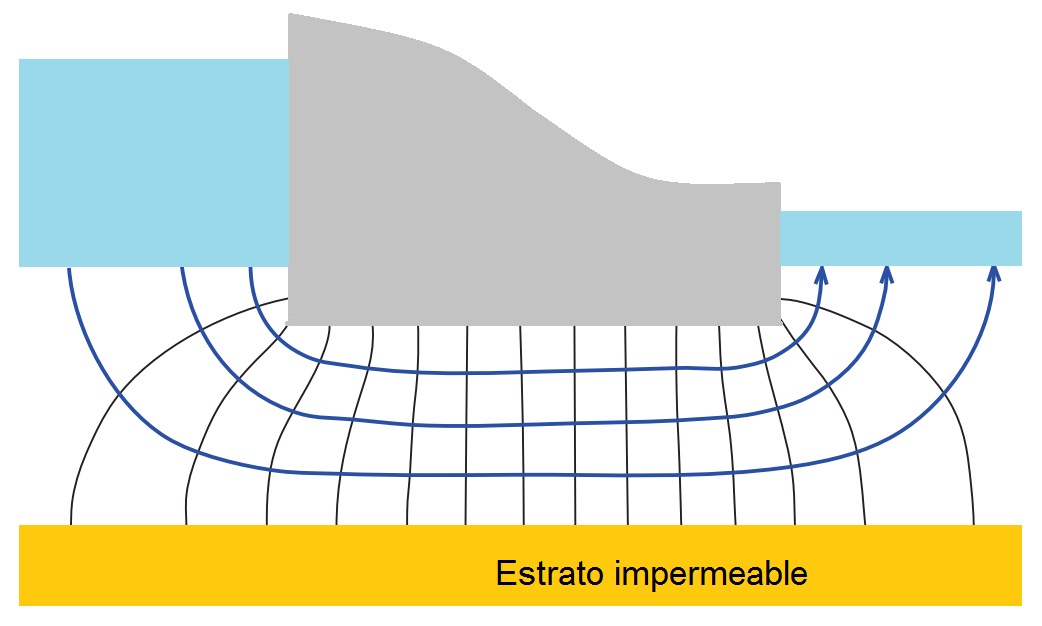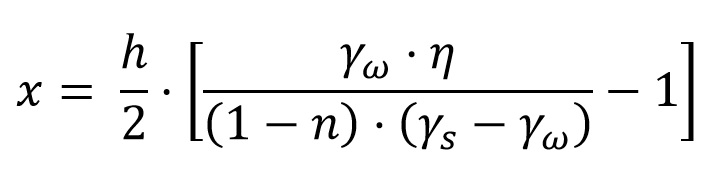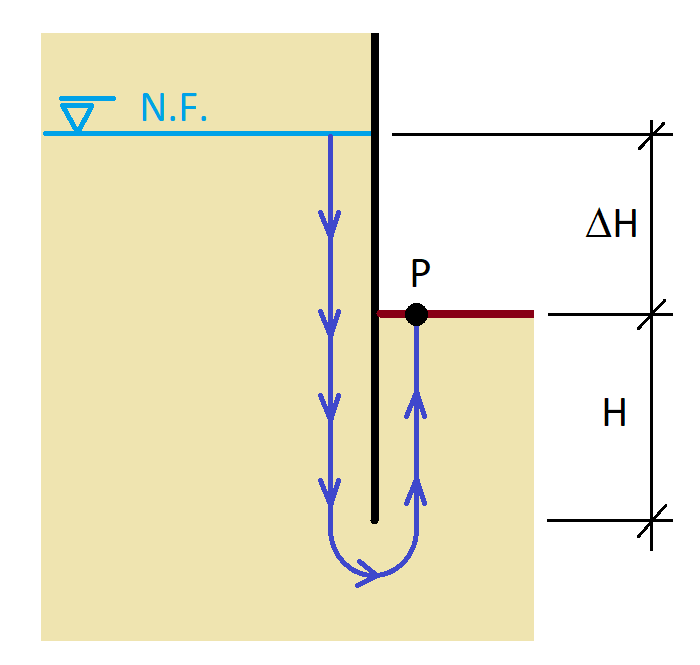
La inestabilidad del fondo o sifonamiento ocurre cuando existe un flujo ascendente, un terreno granular no consolidado puede perder completamente su resistencia a corte y comportarse como un fluido (arenas movedizas, partículas sueltas, como en ebullición), por lo que al fenómeno también se le conoce como fluidificación. Ello ocurre cuando un incremento de la presión intersticial anula la presión efectiva, o dicho de otra forma, cuando las fuerzas producidas por la filtración superan el peso sumergido del suelo. Este fenómeno podría aparecer en pantallas o tablestacas con un empotramiento reducido (Figura 1). En un artículo anterior al que denominamos “El efecto Renard, o por qué un suelo parece que entra en ebullición: Sifonamiento”, explicamos con cierto detalle este fenómeno y resolvimos cuál debería ser la profundidad a la que debería hincarse una tablestaca para evitar que un suelo sin cohesión pierde completamente su resistencia al corte y pasa a comportarse como un fluido.
A este respecto, ya avisamos que una cosa es la profundidad mínima de empotramiento para evitar el sifonamiento y otra bien diferente es calcular el empotramiento necesario de una tablestaca para soportar los esfuerzos de empuje a los que está sometido. Por tanto, el empotramiento real será el mayor de los dos valores. Se recomienda siempre efectuar con detalle los cálculos geotécnicos y estructurales necesarios. Y sobre todo, utilizar el sentido común.
En esta ocasión os paso un problema resuelto donde se calcula la profundidad mínima a la que debe hincarse una tablestaca para evitar el sifonamiento. Este es uno de los casos estudiados en el “Curso de Procedimientos de Construcción de cimentaciones y estructuras de contención en obra civil y edificación”. Espero que os sea de interés.
REFERENCIAS:
- PÉREZ VALCÁRCEL, J.B. (2004). Excavaciones urbanas y estructuras de contención. Ediciones Cat, Colegio Oficial de Arquitectos de Galicia, 419 pp.
- POWERS, J.P. (1992). Construction dewatering: New methods and applications. Ed. Wiley et al., New York.
- PREENE, M.; ROBERTS, T.O.L.; POWRIE, W., DYER, M.R. (2004). Groundwater control: design and practice. CIRIA C515, London.
- TOMLINSON, M.J. (1982). Diseño y construcción de cimientos. URMO, S.A. de Ediciones, Bilbao, 825 pp.
- YEPES, V. (2020). Procedimientos de construcción de cimentaciones y estructuras de contención. Colección Manual de Referencia, 2ª edición. Editorial Universitat Politècnica de València, 480 pp. Ref. 328. ISBN: 978-84-9048-903-1.
- YEPES, V. (2021). Procedimientos de construcción para la compactación y mejora del terreno. Colección Manual de Referencia, 1ª edición. Editorial Universitat Politècnica de València, 426 pp. Ref. 428. ISBN: 978-84-9048-603-0.
- YEPES, V. (2023). Maquinaria y procedimientos de construcción. Problemas resueltos. Colección Académica. Editorial Universitat Politècnica de València, 562 pp. Ref. 376. ISBN 978-84-1396-174-3
Cursos:

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.