Terzaghi – El blog de Víctor Yepes

Control de la mejora de un suelo con ensayos de penetración dinámica

Prueba de penetración dinámica superpesada. https://www.gtklaboratorio.com/prueba-de-penetracion-dinamica-superpesada-en-bilbao

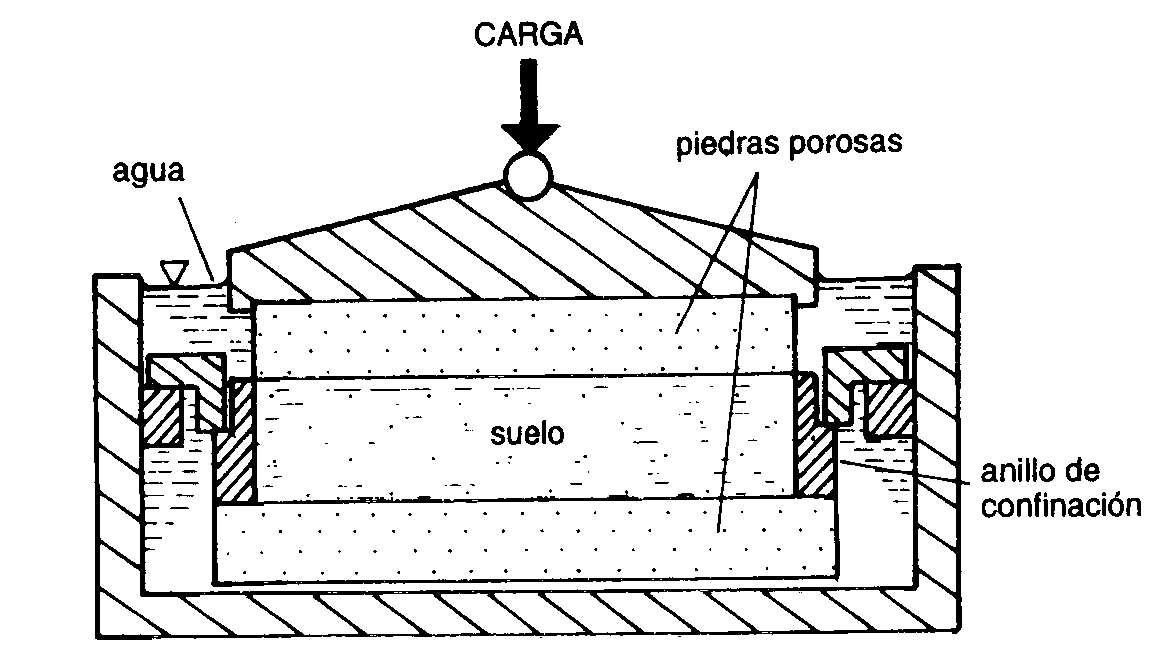
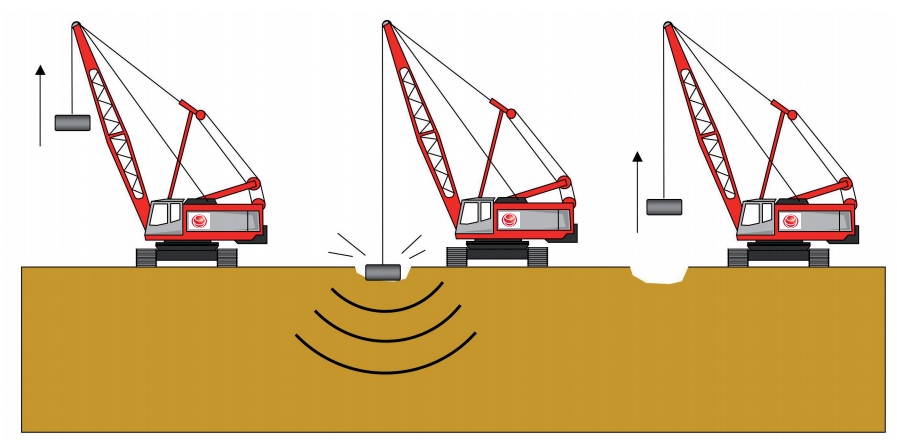
Para comprobar la efectividad de un tratamiento de mejora de suelos, tal y como pudiera ser la compactación dinámica, es necesario verificar que la mejora conseguida es suficientemente buena como para alcanzar los objetivos marcados por el proyecto correspondiente. Una forma económica y sencilla de ensayar el terreno en profundidad consiste en hincar un varillaje con una punta metálica, de forma que, contabilizando el número de golpes necesarios para hacer avanzar dicha punta una longitud determinada, se pudiese correlacionar dicho valor con las características geotécnicas del terreno. A este tipo de pruebas se les conoce con el nombre de ensayos de penetración dinámica.

El ensayo de penetración estándar o SPT (Standard Penetration Test) es quizás uno de los ensayos más frecuentes que se utiliza cuando se realizan sondeos de reconocimiento. De hecho, representan una importante fuente de datos acerca de la resistencia del terreno. Se trata de medir el número de golpes necesario para que se introduzca una cuchara cilíndrica y hueca muy robusta que, además, permite extraer una muestra alterada de su interior. Tanto la cuchara como la masa y la altura a la que caen están normalizadas. La ventaja del SPT es que se permite visualizar el terreno donde se ha realizado la prueba y permite su identificación, e incluso, si el terreno es cohesivo, obtener su humedad. Se trata de ensayos de bajo coste y de alta representatividad, especialmente para suelos granulares y mixtos. La descripción del ensayo se encuentra recogida en la norma UNE 103-800-92. El valor que se obtiene se denomina resistencia a la penetración estándar N_30spt.

Este ensayo nace en 1927 cuando un sondista de la Raymond Concrete Pile propuso a Terzaghi contar el número de golpes necesarios para hincar 1 pie el tomamuestras que se utilizaba para obtener muestras en terrenos no cohesivos. Tras realizar un gran número de ensayos, Terzaghi y Peck (1948) publican sus resultados en su libro “Mecánica de suelos en la ingeniería práctica”. Esta prueba se ha difundido internacionalmente y existen numerosos estudios que permiten relacionar de forma empírica el valor N_30SPT con las propiedades geotécnicas del terreno in situ. Sin embargo, gran parte de las correlaciones corresponden a terrenos arenosos, pues la presencia de gravas oscurece la interpretación de los resultados e incluso puede impedir la realización del ensayo. Por tanto, es un ensayo especialmente indicado para terrenos con una amplia fracción arenosa y lo es menos cuando existe una mayor proporción de finos o de gravas.

Uto y Fijuki (1981) recomiendan corregir el valor de la resistencia a penetración estándar cuando se ensaya a más de 20 metros de profundidad. Skempton (1986) propone factores de corrección a dicho valor en función de la profundidad del ensayo y del diámetro del sondeo, aunque estas correcciones se realizan para suelos granulares, puesto que para los cohesivos dicha influencia es despreciable. Otras correcciones independientes del sistema de ensayo se refieren al nivel freático (Terzaghi y Peck, 1948), a la presión de confinamiento (Gibbs y Holz, 1957), siendo objeto de distintos estudios que están resumidos en Liao y Whitman (1985).

En cuanto a las correlaciones de N_spt con los parámetros geotécnicos del terreno, Terzaghi y Peck (1948) publicaron las primeras correlaciones con la densidad relativa de arenas cuarzíticas, siendo modificadas posteriormente por Skempton (1986). Gibbs y Holtz (1957) comprobaron que se debía introducir la presión de confinamiento en dichas relaciones, y luego Meyerhof (1956) ajustó dichas relaciones. Otras correlaciones referidas al ángulo de rozamiento interno, deformabilidad o potencial de licuación pueden verse en Devicenzi y Frank (1995). Sin embargo, tal y como se comentó anteriormente, las correlaciones sobre terrenos cohesivos se han considerado meramente orientativas, debido a la dispersión de resultados. Sin embargo, hoy en día este criterio se está cuestionando y se están aceptando estas pruebas en todo tipo de terrenos.

Cuando lo que se quiere es disponer de un registro continuo para caracterizar un suelo en profundidad, se puede emplear la prueba de penetración dinámica superpesada o DPSH (Dynamic Probing Super Heavy). Las características del ensayo son distintas a las del SPT. Aquí se utiliza una punta cónica perpendicular al eje de penetración midiéndose el golpeo necesario para profundizar 20 centímetros. Sin embargo, se ha tratado de establecer una correlación entre ambos ensayos que, en el caso de las arenas, el factor de conversión entre ambos ensayos es próximo a la unidad, siempre que estemos entre los 5 y 30 golpes, y siempre que estemos a un máximo de 10 – 15 m, pues a partir de aquí la dispersión aumenta debido al efecto de rozamiento de las varillas, que empieza a ser importante. En el caso de la correlación entre el ensayo Borros o DSPH y el SPT en arcillas, se puede consultar el trabajo de Dapena et al (2000).

Son muchas las correlaciones que se han encontrado entre los ensayos a penetración dinámica. Las equivalencias entre los ensayos parten de una relación de semejanza entre la energía de hinca. Un resumen de los parámetros geomecánicos obtenidos a partir de estos ensayos aplicado a suelos mixtos cohesivos-granulares puede verse en Parra y Ramos (2006).

Todo ello nos lleva a la siguiente conclusión: no es muy fiable establecer correlaciones entre los distintos ensayos de penetración dinámica, especialmente cuando el suelo empieza a ser cohesivo. El tema se complica mucho más cuando el terreno no es natural, sino que se trata de un relleno antrópico heterogéneo. Ello obliga a realizar un estudio en profundidad para establecer dichas correlaciones, siendo aconsejable efectuar un penetrómetro de contraste al lado de un sondeo con SPT.

Os dejo a continuación varios vídeos al respecto de estos ensayos.

También os dejo la maniobra completa del ensayo SPT.

Referencias

Armijo, G.; Blanco, M.A. (2017). Diseño y verificación del tratamiento de mejora del terreno mediante compactación dinámica. Aplicación a un caso real. Interempresas.net.
Devincenzi, M.; Frank, N. (1995). “Ensayos Geotécnicos in situ”, Igeotest, Figueres, Girona.
Gibbs, H.J.; Holtz, W.G. (1957). “Research on Determining the Density of Sands by Spoon Penetration Testing”. Proc. 4^th Conf. On SMFE, London.
Liao, S.; Whitman, R.V. (1986). “Overburden Correction Factors for SPT in Sand”, Journal of Geotechnical Engineering, ASCE, Vol 112, Nº 3.
Menard, L.; Broise Y. (1976). “Theoretical and practical aspects of dynamic consolidation”, Ground Treatment by deep compaction, Institution of Civil Engineers, LONDON, pp. 3-18.
Meyerhof, G.G. (1956). “Penetration Test and Bearing Capacity of Cohesionless Soils”. Journal of Geotechnical Engineering, ASCE, Vol. 91.
Parra, F.; Ramos, L.L. (2006). “Obtención de parámetros geomecánicos a partir de ensayos a penetración dinámica continua en suelos mixtos cohesivos-granulares”. Ingeopres: Actualidad técnica de ingeniería civil, minería, geología y medio ambiente, 145: pp. 20-24.
Skempton, A.W. (1986). “Standard Penetration Test Procedure and Effects in Sandsof Overburden Pressure, Relative Density, Particle Size, Ageing and Overconsolidation”. Geotechnique, 36, pp. 425-437.
Terzaghi, K.; Peck, R.B. (1948). “Soil Mechanics in Engineering Practice”. Ed. John Wiley and Sons, New York.
Uto, K.; Fuyuki, M. (1981). “Present and Future Trend on Penetration Testing in Japan”, Japanese Soc. SMFE.
Dapena, E.; Lacasa, J. García, A. (2000). “Relación entre los resultados de los ensayos de penetración dinámica Borros DPSH y el SPT en un suelo arcilloso”. Actas del Simp. sobre geotecnia de las infraestructuras lineales. Soc. Española de Mec. del Suelo e Ing. Geotécnica.
Yepes, V. (2020). Procedimientos de construcción de cimentaciones y estructuras de contención. Colección Manual de Referencia, 2ª edición. Editorial Universitat Politècnica de València, 480 pp. Ref. 328. ISBN: 978-84-9048-903-1.
Yepes, V. (2021). Procedimientos de construcción para la compactación y mejora del terreno. Colección Manual de Referencia, 1ª edición. Editorial Universitat Politècnica de València, 426 pp. Ref. 428. ISBN: 978-84-9048-603-0.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Conceptos básicos del agua en medio poroso

Figura 1. Esquema de acuífero. https://es.wikipedia.org/wiki/Archivo:Aquifer_es.svg

Cualquier curso de geotecnia básica dedica una parte importante de su temario a describir y caracterizar el agua en el suelo, especialmente el flujo en medios porosos y la incidencia de las presiones efectivas en la deformación de los suelos.

En este artículo vamos a recordar algunos conceptos básicos que, de una u otra forma, influyen directamente en los procedimientos constructivos, especialmente cuando se trata de controlar el agua. Se remite al lector a la bibliografía básica para profundizar más en estos temas.

Acuífero: terreno por donde circula el agua. Al límite impermeable inferior del acuífero se le denomina muro y al superior techo. Si el agua se encuentra en contacto con la atmósfera a través de los poros o fisuras existentes en la zona no saturada, se denomina acuífero libre. En cambio, en un acuífero confinado, el techo se encuentra a presión superior a la atmosférica.
Acuicludo: formación geológica que conteniendo agua en su interior, incluso hasta la saturación, no la transmite y, por tanto, no es posible su explotación (caso de terrenos arcillosos).
Acuitardo: formación geológica que transmiten muy lentamente el agua, por lo que tampoco son aptos para la captación. Sin embargo, en condiciones especiales, permiten una recarga vertical de otros acuíferos. Es el caso de un estrato de arcillas limosas o arenosas.
Nivel freático: lugar geométrico de los puntos donde la presión del agua es la atmosférica. Es el nivel que alcanza la superficie del agua en pozos de observación en libre comunicación con los vacíos del suelo in situ. Por encima del nivel freático existe el agua capilar donde su presión es menor que la atmosférica. En un punto concreto, en un pozo, se habla de nivel piezométrico, que si se encuentra por encima de la superficie del terreno, se dice que existen “condiciones artesianas”.
Coeficiente de almacenamiento: cantidad de agua que cede un prisma de acuífero de base cuadrada unitaria cuando se le deprime la unidad. Es adimensional. Su valor oscila normalmente entre 0,2 y 0,4 en acuíferos libres, oscilando entre 10^-5 y 10^-3 en los acuíferos cautivos y semiconfinados, al entrar en juego los efectos mecánicos del terreno o de la propia agua.

Figura 2. Esquema de acuífero libre y confinado (Bouwer, 1987)

Porosidad: porcentaje del volumen total de un suelo o roca que está ocupado por poros. Estos poros estarán rellenos de agua si el material está saturado, o de aire y agua si no lo está. Si solo se considera el volumen de los poros que están interconectados, se denomina “porosidad eficaz”. En los acuíferos libres el coeficiente de almacenamiento coincide con la porosidad eficaz.
Índice de poros o huecos: razón entre el volumen de poros y el volumen de sólidos.
Humedad: relación entre el peso del agua que contiene un suelo y el peso del suelo seco.
Grado de saturación: porcentaje del volumen de huecos ocupados por el agua.

Carga hidráulica total: también llamado potencial, es la energía por unidad de peso (expresada como una altura) en un determinado punto de un fluido en movimiento. Donde H es la carga hidráulica total, z la altura geométrica, u/γ_w la altura de presión, siendo u la presión del agua en el punto considerado y γ_w el peso específico del agua y v²/2g la altura de velocidad, siendo v la velocidad del flujo en el punto considerado y g la aceleración de la gravedad. Todos estos términos tienen unidades de longitud. Si el agua está en reposo (condiciones hidrostáticas), o bien se desprecia la velocidad por ser muy baja (caso de la circulación del agua en medio poroso), la carga total es la altura piezométrica.

Líneas de corriente o líneas de flujo: son las curvas por las que se mueven las partículas fluidas, invariables en el transcurso del tiempo. A medida que el agua circula a través del suelo, modifica su velocidad y potencial.
Líneas equipotenciales: lugares geométricos del flujo donde la altura piezométrica es constante.

Figura 3. Red de flujo, formada por líneas equipotenciales (Ψ) y líneas de corriente (Φ)

Teorema de Bernouilli: en el caso ideal de un fluido perfecto e incompresible sujeto a un flujo permanente y estacionario, la carga hidráulica total se mantiene constante entre dos puntos cualesquiera del fluido a lo largo de una línea de corriente. Como un fluido real no es perfecto, cualquier obstáculo al flujo produce una pérdida de carga. De hecho, existe flujo entre dos puntos si existe una diferencia en la carga hidráulica, de forma que el agua circula del punto de mayor a menor potencial. Si se añade energía H al caudal mediante una bomba, y se consideran las pérdidas h_r, del punto 1 al punto 2, la ecuación queda:

Coeficiente de permeabilidad: k, mide la facilidad para que el agua circule a través de un suelo. También se llama conductividad hidráulica, y tiene unidades de velocidad, normalmente cm/s. La permeabilidad implica una posibilidad de recorrido y exige la existencia de vacíos o huecos continuos. La permeabilidad depende de factores intrínsecos al acuífero y extrínsecos, que dependen del fluido, y son su viscosidad y su peso específico. Según Hazen, en arenas uniformes, la permeabilidad es proporcional al cuadrado del diámetro eficaz (D₁₀ ).
Permeabilidad equivalente horizontal: el flujo atraviesa horizontalmente un conjunto de n estratos, con una permeabilidad cada uno de k_i y un espesor e_i. El caudal equivalente será la suma de los caudales, por lo que la permeabilidad equivalente, k_h vale lo siguiente:

Permeabilidad equivalente vertical: el flujo atraviesa verticalmente un conjunto de n estratos, con una permeabilidad cada uno de k_i y un espesor e_i. El caudal a lo largo de los estratos, y cada estrato tendrá un gradiente distinto i_i, por lo que igualando las pérdidas de carga y despejando, obtenemos la permeabilidad equivalente k_v, que vale lo siguiente:

Gradiente hidráulico: i, se define como la pérdida de carga (altura piezométrica) por unidad de longitud recorrida. Es un vector cuya dirección se orienta con los potenciales decrecientes.

Ley de Darcy: la velocidad del fluido en medio poroso es proporcional al gradiente hidráulico a través del coeficiente de permeabilidad. No es una propiedad intrínseca del suelo y tiene unidades de velocidad. Aquí se ha supuesto un flujo laminar en medio poroso y una velocidad media a través de una sección “macroscópica” de suelo, es decir, la velocidad aparente a lo largo de las líneas de flujo.

Transmisividad: caudal que se filtra a través de una franja vertical de terreno, de ancho unidad y de altura igual al espesor saturado, bajo un gradiente unidad, a una temperatura determinada y durante la unidad de tiempo. Sus unidades son las de una velocidad multiplicada por una longitud.
Ecuación de Laplace: modeliza un flujo estacionario en medio poroso homogéneo e isótropo de un fluido incompresible, en un suelo de peso específico constante y saturado. De difícil solución analítica, se puede resolver gráficamente dibujando dos familias de curvas ortogonales entre sí, las líneas equipotenciales (Ψ) y las líneas de corriente (Φ), que forman la red de flujo. Para dibujar la red de flujo hay que considerar que las fronteras impermeables constituyen líneas de corriente y las fronteras permeables (como una lámina de agua) es una línea equipotencial. Al cortarse ambas familias de líneas, se deben obtener “cuadrados curvilíneos”.

Red de flujo: una vez dibujada la red, la pérdida de carga total se distribuye de forma uniforme entre las equipotenciales, todos los canales de flujo transportan el mismo caudal, y un canal de flujo es el comprendido entre dos líneas de corriente. Las principales aplicaciones de las redes de flujo son: calcular las presiones del agua subterránea en unas determinadas líneas o superficies, estimar los caudales del agua subterránea y calcular los gradientes hidráulicos.

Fuerzas de filtración o de arrastre: son fuerzas másicas (fuerza por unidad de volumen) que el agua ejerce sobre el terreno al circular por sus poros. El módulo de estas fuerzas por unidad de volumen es el producto del peso específico del agua por el gradiente. La fuerza de filtración tiene la dirección y el sentido del flujo.

Presión efectiva: es la presión que se transmite grano a grano, siendo la diferencia entre las presiones totales y las intersticiales. Según el postulado de Terzaghi, la resistencia al esfuerzo cortante y el cambio de volumen de un suelo dependen de la magnitud de la presión efectiva y sus variaciones.

Os voy a dejar algunos vídeos explicativos de estos conceptos. Espero que os sean de utilidad.

Referencias:

BOUWER, H. (1978). Groundwater Hidrology. Mc Graw-Hill Book Co., New York, 480 pp.
DAS, B. (2005). Fundamental of Geotechnical Engineering – 2nd ed, Technomic Publishing Co.
GONZÁLEZ DE VALLEJO, L.I. et al. (2004). Ingeniería Geológica. Pearson, Prentice Hall, Madrid.
POWERS, J.P. (1992). Construction dewatering: New methods and applications. Ed. Wiley et al., New York.
PREENE, M.; ROBERTS, T.O.L.; POWRIE, W., DYER, M.R. (2004). Groundwater control: design and practice. CIRIA C515, London.
YEPES, V. (2020). Procedimientos de construcción de cimentaciones y estructuras de contención. Colección Manual de Referencia, 2ª edición. Editorial Universitat Politècnica de València, 480 pp. Ref. 328. ISBN: 978-84-9048-903-1.
YEPES, V. (2021). Procedimientos de construcción para la compactación y mejora del terreno. Colección Manual de Referencia, 1ª edición. Editorial Universitat Politècnica de València, 426 pp. Ref. 428. ISBN: 978-84-9048-603-0.

Cursos:

Curso de procedimientos de contención y control del agua subterránea en obras de Ingeniería Civil y Edificación

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Empujes sobre entibaciones según Terzaghi y Peck

Figura 1. Entibación en excavación de zanja. https://commons.wikimedia.org/wiki/File:Sbh_s600.JPG

Ya se habló en un artículo anterior de la altura crítica, que si se sobrepasa, obliga a entibar una excavación. Este es un aspecto de gran importancia en la seguridad de las personas. Para ello resulta fundamental el cálculo de los empujes del terreno sobre la entibación para dimensionar correctamente los elementos constitutivos de esta estructura auxiliar.

La deformación que se desarrolla en el terreno al ir entibando una excavación, poniendo puntales de arriba hacia abajo, es diferente a la que desarrollan la condición de empuje activo en los muros. Este hecho provoca que la distribución real de los empujes sobre una entibación sea diferente a la clásica ley triangular que aparecen en los muros. Esto se debe, entre otros motivos, a que la entibación va a girar respecto a un punto situado en la parte superior (primer apuntalamiento), frente al típico muro en ménsula, donde el giro se realiza, aproximadamente, en la base de la estructura.

En la Figura 2 podemos ver que los empujes reales no crecen proporcionalmente con la profundidad y que, en el fondo de la excavación, acaban anulándose. Por tanto, la parte superior, que se apuntala desde el primer momento, recibe unos empujes superiores a los de la ley triangular, y en la parte inferior, son menores. La ley de empujes, por tanto, se aproxima a una parábola.

Figura 2. Empujes reales de forma parabólica sobre entibaciones

Terzaghi y Peck (1967) propusieron algunos esquemas simplificados útiles para determinados suelos típicos. Son los denominados “diagramas de presión aparente“, deducidos a partir de medidas realizadas en diferentes obras a mediados del siglo XX (Berlín, Múnich, Chicago, Nueva York y Oslo) en entibaciones apuntadas, no ancladas, de más de 6 m de profundidad. No se trata realmente de unos diagramas de empujes únicos, sino de las envolventes empíricas de los distintos diagramas reales que se observan en una fase de excavación y que pueden ser bastante complicados (secuencia de construcción, temperatura, acomodo entre pantalla y apoyos, etc.).

Teniendo en cuanto los valores a, b y c de la Figura 3, se pueden estimar la ley de empujes en función de la Tabla 1 (Izquierdo, 2001). Hay que tener presente que estos empujes, sacados de mediciones realmente tomadas en obra, son aplicables a los empujes sobre entibaciones, por lo que no es de aplicación directa a superficies continuas y mucho más rígidas como los muros pantalla.

Figura 3. Distribuciones propuestas para empuje sobre entibaciones

Tabla 1. Procedimiento empírico de Terzaghi y Peck (1967) para determinar las cargas sobre los puntales en una excavación entibada (Izquierdo, 2001)

En la Tabla 1, K_a es el coeficiente de empuje activo, c_u la cohesión del terreno sin drenaje y γ su peso específico.

REFERENCIAS:

GARCÍA VALCARCE, A. (dir.) (2003). Manual de edificación: mecánica de los terrenos y cimientos. CIE Inversiones Editoriales Dossat-2000 S.L. Madrid, 716 pp.
GONZÁLEZ CABALLERO, M. (2001). El terreno. Edicions UPC, Barcelona, 309 pp.
IZQUIERDO, F.A. (2001). Cuestiones de geotecnia y cimientos. Editorial Universidad Politécnica de Valencia, 227 pp.
LAMBE, T.W.; WHITMAN, R.V. (1996). Mecánica de suelos. Limusa, México, D.F., 582 pp.
MINISTERIO DE FOMENTO (2002). Guía de Cimentaciones. Dirección General de Carreteras.
MINISTERIO DE LA VIVIENDA (2006). Código Técnico de la Edificación
TERZAGHI, K.; PECK, R. (1967). Soil Mechanics in Engineering Practice. 2nd Edition, John Wiley, New York.
YEPES, V. (2020). Procedimientos de construcción de cimentaciones y estructuras de contención. Colección Manual de Referencia, 2ª edición. Editorial Universitat Politècnica de València, 480 pp. Ref. 328. ISBN: 978-84-9048-903-1.

Cursos:

Curso de estructuras auxiliares en la construcción: andamios, apeos, entibaciones, encofrados y cimbras.

Curso de Procedimientos de Construcción de cimentaciones y estructuras de contención en obra civil y edificación.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Paradoja de Zenón en la parsimonia del asiento de los suelos saturados

Figura 1. Inclinación de la torre de Pisa

Una de las paradojas que planteó el filósofo Zenón de Elea es que si para ir a un lugar recorres primero la mitad de la distancia, luego la mitad de la distancia que te queda por recorrer, y así hasta el infinito, nunca llegarás a tu destino, aunque estés toda la vida andando. Esta paradoja se solucionó matemáticamente en el siglo XIX al aceptar que la suma de 1/2 + 1/4 + … suman 1. Pues bien, un terreno saturado al que sometemos a una carga va a asentar de forma indefinida, pero no superará un valor tope determinado. Veamos esto con mayor detalle.

En un artículo anterior vimos hablamos del Principio de Terzaghi, por el cual un terreno se deforma solo cuando existe un cambio en sus tensiones efectivas. Cuando se carga un terreno saturado, éste tiene la costumbre provocar asientos que se incrementan con el tiempo, siempre que sea posible el drenaje. Esto plantea la pregunta de si los asientos crecerán de forma indefinida con el tiempo. Afortunadamente, el asiento tiende asintóticamente a una magnitud última a la cual se llegará, eso sí, en tiempo infinito.

Pero empecemos por el principio. En presencia de un sólido homogéneo, isótropo y linealmente elástico, la teoría de la elasticidad nos permite conocer perfectamente la deformación que tendrá ante un incremento de cargas. Para ello basta conocer el módulo de elasticidad E y el coeficiente de Poisson ν. Es más, si estamos ante este tipo de terreno y conocemos las ecuaciones de Hooke en términos efectivos (es decir, conocemos E‘ y γ’, obtenidos en suelo drenado, a largo plazo), entonces tenemos herramientas para averiguar la deformación del terreno, tal y como vimos en el artículo que donde hablábamos de los asientos de cargas rectangulares en el semiespacio de Boussinesq. Este método sería válido para cargas de servicio o de trabajo, alejadas de la carga de rotura (factor de seguridad del orden de 3), que probablemente generen asientos elásticos. El método elástico será tanto más aceptable cuanto más se asemeje el comportamiento del suelo al del sólido lineal-elástico, como es el caso de los suelos granulares o las arcillas fuertemente sobreconsolidadas, bajo presiones normales de cimentación.

Sin embargo, no vamos a tener tanta suerte. El comportamiento del suelo es más complejo. De hecho, la deformación ocurrirá, tal y como se ha comentado anteriormente, cuando las presiones efectivas empiecen a cambiar. Y eso tendrá lugar si se permiten disipar las presiones intersticiales del terreno. Por tanto, las deformaciones van a depender, entre otros factores, de la permeabilidad. Terrenos altamente permeables, como gravas o arenas, van a deformar rápidamente, puesto que el agua drenará con mucha facilidad. Pero terrenos más impermeables como las arcillas, el proceso se dilatará en el tiempo. Es el fenómeno conocido como consolidación.

Por tanto, ante un terreno saturado, tenemos tres tipos de consolidación. La consolidación inicial la provoca un aumento de la presión total, que provoca un cambio de volumen debido a efectos como la disolución de las burbujas de aire, el cierre de fisuras o la reordenación de las partículas, entre otras posibles causas. La consolidación primaria, es provocada por el aumento de la presión efectiva como consecuencia de la disipación de las sobrepresiones intersticiales. Por último, la consolidación secundaria se produce a tensión efectiva constante, es decir, una vez disipada la sobrepresión intersticial y se debe a factores como la fluencia por desplazamientos y reorientaciones de partículas, o bien a la descomposición de la materia orgánica del suelo, entre otras posibles causas.

Figura 2. Curva de consolidación de un suelo saturado.

Para determinar tanto la magnitud de la deformación de un suelo al aumentar la tensión efectiva a la que está sometido (curva edométrica), como la velocidad a la que ocurre el asiento de consolidación (curva de consolidación), se utiliza el ensayo edométrico. De este ensayo y sus características hablaremos en otros artículos.

Pero aquí lo que queremos es ver cómo evolucionan los asiento con el tiempo durante el proceso de consolidación. En un proceso unidimensional, la ecuación que gobierna dicho proceso es la siguiente:

donde C_v es el denominado coeficiente de consolidación vertical, que depende del nivel de tensiones existente y cuyas unidades son [L²]/[T]. Este coeficiente en una arcilla puede deducirse de un ensayo edométrico de una muestra inalterada. Su valor tipo oscila entre 0,4 x 10^-4 y 3 x 10^-3cm²/s, y los valores deducidos in situ oscilan entre 0,7 x 10^-4 y 250cm²/s (González Caballero, 2001).

Si definimos como grado de consolidación U la relación entre el asiento experimentado en un instante por el suelo respecto al asiento total, podemos utilizar U como variable auxiliar adimensional para resolver la ecuación diferencial anterior.

Si llamamos factor de tiempo a T_v, éste se encuentra relacionado con U. La solución simplificada de la ecuación diferencial, suponiendo que el incremento de presión total es uniforme o lineal en el caso del doble drenaje, nos lleva a dos ecuaciones sencillas, que son las siguientes:

Estas expresiones las hemos dibujado en la Figura 3, donde se relaciona U con T_v. Se puede observar que para el grado de consolidación del 100%, el factor de tiempo se hace infinito. No obstante, se puede considerar que un factor de tiempo T_v = 2 corresponde prácticamente al final de la consolidación primaria.

Figura 3. Factor de tiempo en función del grado de consolidación

Además, el coeficiente de consolidación vertical C_v está relacionado con el factor de tiempo T_v, con la distancia libre de drenaje d y con el tiempo t a través de la siguiente expresión:

Por tanto, se puede saber el tiempo que tardará en asentar un suelo saturado para alcanzar un grado de consolidación determinado conociendo la distancia libre de drenaje y el coeficiente de consolidación vertical. Los cálculos pueden realizarse rápidamente utilizando la gráfica de la Figura 4. Se ha dibujado el eje vertical en escala logarítmica. Cada función indica una longitud libre de drenaje distinta.

Figura 4. Relación entre el producto del coeficiente de consolidación y el tiempo con el grado de consolidación y la distancia libre de drenaje.

Vamos a hacer un cálculo aproximado utilizando la Figura 4. Si suponemos una arcilla con un coeficiente de consolidación C_v = 1,0 m²/año, en el periodo de 1 año, con una longitud de drenaje de 1 m, se habrá superado más del 90% del asiento previsto, pero si la longitud de drenaje es de 2 m, no llegaremos al 60% del asiento.

Se deja al lector curioso la demostración de que si la longitud de drenaje la dividimos por n, entonces el tiempo que se tardará en alcanzar el mismo grado de consolidación se divide por n² . Así, por ejemplo, una capa de arcillas dispuesta entre dos capas de material granular tardará en alcanzar un mismo asiento en la cuarta parte del tiempo que si dicha capa estuviese dispuesta entre una capa granular y otra impermeable.

Referencias:

DAS, B. (2005). Fundamental of Geotechnical Engineering – 2nd ed, Technomic Publishing Co.
GONZÁLEZ CABALLERO, M. (2001). El terreno. Edicions UPC, 309 pp.
GONZÁLEZ DE VALLEJO, L.I. et al. (2004). Ingeniería Geológica. Pearson, Prentice Hall, Madrid.
IZQUIERDO, F.A. (2001). Cuestiones de geotecnia y cimientos. Editorial Universidad Politécnica de Valencia, 227 pp.
YEPES, V. (2020). Procedimientos de construcción de cimentaciones y estructuras de contención. Colección Manual de Referencia, 2ª edición. Editorial Universitat Politècnica de València, 480 pp. Ref. 328. ISBN: 978-84-9048-903-1.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

La magia de las tensiones efectivas en geotecnia

Karl von Terzaghi (1883 – 1963) ://es.wikipedia.org/wiki/Karl_von_Terzaghi

Os presento uno de los conceptos básicos utilizados en geotecnia que, en ocasiones, complica a muchos de mis estudiantes cuando en la asignatura Procedimientos de Construcción explicamos algunos aspectos de la mejora de terrenos (columna de grava, precarga, drenes verticales, etc.). Se trata del concepto de “tensiones efectivas”, que hoy es sencillo, pero que confundió a numerosos ingenieros durante mucho tiempo.

La ley de elasticidad Hooke, donde la aplicación de una fuerza supone una deformación proporcional a la misma, desde luego no era aplicable directamente a muchos problemas que los ingenieros tenían con el terreno. Desde siempre se conoce que el comportamiento mecánico del suelo es algo complejo, pero era sorprendente, por ejemplo, que una carga aplicada sobre un terreno con nivel freático elevado, no se deformase. Y lo más sorprendente, es que, al cabo de cierto tiempo, sin modificar el estado de cargas, el terreno se deformara “por arte de magia”.

Este problema ingenieril traía de cabeza a muchos ingenieros hasta los primeros años del siglo XX. Si se analiza un suelo desde el punto de vista “microscópico”, la transmisión de esfuerzos se realiza mediante cadenas de partículas, unas apoyadas con otras. Lo que es peor, si este suelo es de partículas tan finas como son las arcillas, la fuerza de gravedad pierde importancia frente a las fuerzas fisico-químicas. La solución es entender la mecánica del suelo como si fuera un medio continuo, es decir, desde el punto de vista “macroscópico”. Tal simplificación necesita un marco teórico de partida que fue postulado por uno de los grandes genios y padre de la mecánica de suelos: Karl von Terzaghi (Praga, 2 de octubre de 1883 – Winchester, Massachusetts, 25 de octubre de 1963).

Su aportación genial fue formular un postulado acerca de lo que denominó como “tensiones efectivas“. Como todo postulado que se precie, se trata de una proposición no evidente por sí misma, ni demostrada, pero que se acepta, ya que no existe otro principio al que pueda ser referida. De todos modos, las evidencias empíricas del correcto funcionamiento de este postulado hace que hoy día se admita en el campo de la mecánica de suelos porque permite explicar multitud de problemas geotécnicos. Terzaghi definió el concepto de tensiones efectivas, en 1923, partiendo de resultados experimentales. De forma muy simple, diremos que las tensiones efectivas que actúan en el terreno son el exceso de tensión sobre la presión intersticial del agua presente en él. Y lo más importante de todo ello es que son las tensiones efectivas las que pueden provocar cambios en la deformación del terreno. Pero vamos a reproducir (González de Vallejo et al., 2004) las dos partes fundamentales del enunciado de su postulado, según las propias palabras de Terzaghi:

“Las tensiones en cualquier punto de un plano que atraviesa una masa de suelo pueden ser calculadas a partir de las tensiones principales totales σ₁, σ₂ y σ₃ , que actúan en ese punto. Si los poros del suelo se encuentran rellenos de agua bajo una presión u, las tensiones principales totales se componen de dos partes. Una parte, u, llamada presión neutra o presión intersticial, actúa sobre el agua y sobre las partículas sólidas en todas direcciones y con igual intensidad. Las diferencias σ’₁ = σ₁ – u, σ’₂ = σ₂ – u, σ’₃ = σ₃ – u representan un exceso de presión sobre la presión neutra u, y actúan exclusivamente en la fase sólida del suelo. Estas fracciones de las tensiones principales totales se denominan tensiones efectivas.

Cualquier efecto medible debido a un cambio de tensiones, tal como la compresión, la distorsión o la modificación de la resistencia al corte de un suelo, es debido exclusivamente a cambios en las tensiones efectivas”.

Podemos sacar varias conclusiones directamente de este postulado:

Si en un suelo saturado no hay cambios de volumen ni de distorsión, eso significa que las tensiones efectivas no han cambiado.
Como el agua no es capaz de soportar tensiones tangenciales, las que existan en un suelo saturado la debe absorber el esqueleto sólido del suelo.
Si a un suelo saturado se le permite el drenaje (disipación de la tensión intersticial), entonces este suelo se deforma y se modifica su resistencia a corte. Al fenómeno se denomina consolidación.

Como entretenimiento práctico podéis deducir cómo la tensión efectiva en un punto de un estrato situado bajo nivel freático es igual al producto de la profundidad del punto en el estrato multiplicado por el peso específico sumergido del material de dicho estrato. Asimismo, si existen distintos estratos, es la suma de las alturas de los posibles estratos por sus correspondientes pesos específicos sumergidos.

Referencias:

DAS, B. (2005). Fundamental of Geotechnical Engineering – 2nd ed, Technomic Publishing Co.
GONZÁLEZ DE VALLEJO, L.I. et al. (2004). Ingeniería Geológica. Pearson, Prentice Hall, Madrid.
YEPES, V. (2020). Procedimientos de construcción de cimentaciones y estructuras de contención. Colección Manual de Referencia, 2ª edición. Editorial Universitat Politècnica de València, 480 pp. Ref. 328. ISBN: 978-84-9048-903-1.

Cursos:

Curso de Procedimientos de Construcción de cimentaciones y estructuras de contención en obra civil y edificación.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Diagramas de carga-deflexión en la compactación mecánica de suelos

La compactación mecánica está basada en las relaciones entre las tensiones y las deformaciones o deflexiones causadas por una carga compresora.

Si se analiza el ensayo realizado sobre una probeta de suelo cilíndrica, permaneciendo la superficie lateral libre y en cuya base superior aplicamos una carga mediante una chapa metálica, con un valor que vaya aumentando a velocidad constante, se obtiene el diagrama de carga-deflexión como el de la Figura 2. En este ensayo, una vez alcanzado determinado valor en la carga, la probeta rompe. Asimismo, la pendiente de la curva cargas-asientos correspondiente a cada ciclo permite calcular el módulo de deformación del suelo.

Figura 2. Tensión-deformación en una probeta con paredes laterales libres

La curva permite comprobar ciertos fenómenos significativos. El primero de ellos es que si al llegar al punto 3 dejamos de aumentar la carga, sigue la probeta deformándose hasta estabilizarse en el punto 4 al cabo de cierto tiempo. Este efecto es acusado en suelos plásticos y húmedos por su dificultad en evacuar el aire y el agua. El segundo fenómeno es que si a partir de un punto tal como el 1 descargamos a la misma velocidad que veníamos cargando, la probeta recupera parte de su deformación, hasta llegar a 2 cuando ya no existe tensión. Si a partir de este punto repetimos el proceso, la nueva curva se aproxima a la original hasta ser tangente con ella. Estas dos ramas, de compresión y de descompresión, no se confunden, sino que forman un lazo nominado de histéresis.

Si este experimento se realiza con un terreno natural, y otro recompuesto de la rotura de los anteriores ensayos, y ambos se vuelven a testar con la misma humedad, se observa que a igualdad de cargas, los suelos recompuestos o amasados rompen antes y sufren mayor deformación. Análogamente, si experimentamos a mayores velocidades de incremento de carga, las deformaciones son menores ya que no da tiempo suficiente a evacuar aire y agua de la muestra.

El segundo tipo de ensayo propuesto sería someter la probeta cilíndrica a un proceso de cargas escalonado, de forma que permanezca constante la compresión durante un periodo de tiempo dilatado que garantice que se alcanza el alargamiento límite para dicha carga. A su vez, la probeta tendrá impedida su deformación lateral, siendo porosas las bases del cilindro, pudiendo así aplicar cargas de mayor magnitud. En este caso sólo existe deformación vertical siendo la lateral nula, hablándose entonces de deformación edométrica, por ser el edómetro el aparato en el cual se realiza este experimento. Por cierto, edómetro viene del griego “oidos“, hinchamiento, por ser la medida de la expansividad de los suelos en contacto en el agua, una de sus primeras aplicaciones.

En este caso, la curva obtenida presenta las mismas características que la anterior. Si no se descarga, la curva (0135) se denomina de compresión noval. Al descargar, nos movemos de forma lineal por la rama de descarga. Se llama presión de preconsolidación la máxima que ha sufrido el material en su historia, siendo por tanto que un suelo o está en la rama elástica o en la tensión de preconsolidación.

Se distinguen tres tipos de asientos al realizar un ensayo edométrico. La consolidación inicial es un asiento independiente del fenómeno de consolidación y que está asociado a deformaciones debidas al cierre de fisuras de la muestra, a rozamientos y huelgos del sistema de aplicación de la carga, etc. La consolidación primaria se rige por la teoría de la consolidación, es decir, existe un asiento debido a la expulsión del agua como consecuencia de la sobrepresión aplicada. Por último, la consolidación secundaria se debe a fenómenos viscosos y de reajuste de la estructura del suelo una vez las sobrepresiones se han anulado, y tampoco se debe al fenómeno de consolidación. La teoría de la consolidación está basada en el principio de Terzaghi, y plantea que un suelo saturado y poco permeable reacciona inicialmente a un cambio tensional como si no cambiara de volumen, generando sobrepresiones intersticiales. A medida que éstas se van disipando hacia los contornos drenantes, las tensiones totales transmitidas inicialmente se transforman, gradualmente, en presiones efectivas, y el suelo se deforma.

Se llaman suelos normalmente consolidados aquellos en los que la tensión efectiva actual es la máxima que han tenido en su historia, y suelos sobreconsolidados o preconsolidados los que han soportado en el pasado una tensión superior a la actual. Es evidente que cuanto antes se hablaba de un suelo remoldeado en anteriores ensayos, este es, por definición, sobreconsolidado.

A continuación os dejo un vídeo sobre el ensayo edométrico. Espero que os sea de interés.

Referencia:

YEPES, V. (2021). Procedimientos de construcción para la compactación y mejora del terreno. Colección Manual de Referencia, 1ª edición. Editorial Universitat Politècnica de València, 426 pp. Ref. 428. ISBN: 978-84-9048-603-0.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Compactación dinámica

La compactación dinámica (“dynamic compaction”, DC) es una técnica que mejora la capacidad portante de los suelos mediante al dejar caer una masa desde cierta altura. El nombre de compactación dinámica no refleja con exactitud los procesos reales de carga y transmisión de energía, por lo que también suele llamarse compactación dinámica profunda (“deep dynamic compaction”). Uno de los mitos de la compactación dinámica es que se trata de un tratamiento superficial del suelo debido a que las cargas se aplican en la superficie. Pero, a diferencia de la compactación superficial, es un proceso de densificación que llega a profundidades de 10-12 m. Tras el impacto, se crean cráteres de hasta dos metros o más de profundidad, que deben ser rellenarse y compactar. La densificación en profundidad se produce como resultado de la energía de las ondas dinámicas que se transmite a través del suelo. El tratamiento se aplica en edificios industriales, plataformas portuarias y aeroportuarias, terraplenes viarios y ferroviarios, etc. Además, es idóneo para obras extensas, con rendimientos de más de 10000 m² por mes.

El principio de dejar caer grandes masas sobre la superficie del suelo para mejorarlo en profundidad se ha empleado desde hace tiempo. Menard y Broise (1976) hacen referencia a dibujos muy antiguos que sugieren que la técnica se utilizó en China desde hace centurias. Los romanos también la utilizaron en sus construcciones antes del 100 a.C. En los Estados Unidos se empleó un antiguo cañón para compactar ya en el año 1871 (Lundwall, 1968). También en la antigua Unión Soviética se compactaron loess con buenos resultados, si bien con pesos y alturas de caída mucho menores a las actuales (Faraco, 1980). En los años 40 se empleó este procedimiento constructivo en la construcción de un aeropuerto en China y un área portuaria en Dublín. Sin embargo la técnica actual se puede fechar en 1970, cuando Louis Menard patentó este método en Francia, favorecido sin duda por la aparición de las gigantescas grúas montadas sobre orugas. En Gran Bretaña y en Estados Unidos se empezó a utilizar en los años 1973 y 1975, respectivamente.

Hoy en día, es habitual el uso de pesos que oscilan entre 1 y 30 t, con alturas de caída de entre 10 y 30 m, a veces más. Los pesos son de acero para soportar las fuerzas dinámicas repetitivas. Normalmente, se utiliza una grúa para dejar caer el peso, aunque también existen equipos especiales. Las grúas deben permanecer en buenas condiciones pues no se diseñan para cargas dinámicas repetitivas.

Figura 2. Esquema de la ejecución de la compactación dinámica. Cortesía de Menard

Este tipo de tratamiento depende de las características del suelo y de la energía empleada. En principio, se puede utilizar en suelos granulares, saturados o no. Asimismo, ofrece buenos resultados en rellenos artificiales heterogéneos, que difícilmente se mejorarían con otros procedimientos. La mejora se traduce en un aumento de la capacidad portante y una reducción de los asientos, incluidos los diferenciales. Es un método bien adaptado y empleado para prevenir la licuefacción de suelos. La compactación dinámica permite, incluso, cimentar con zapatas convencionales, pues proporciona una capacidad portante al suelo de hasta 100-150 kPa. Además, es una solución económica cuando se compara con la excavación y sustitución del suelo, la precarga o las inyecciones. Los costes son aproximadamente 2/3 respecto a las columnas de grava, con un ahorro de hasta el 50% comparado con la compactación profunda. Se pueden conseguir rendimientos de 300 a 600 m²/día (García Valcarce et al., 2003).

La compactación dinámica se emplea para densificar suelos flojos, saturados y sin cohesión, reduciendo la potencial licuefacción del terreno. En este sentido, el proceso de densificación es similar al de la vibro-compactación. Es una de las mejores alternativas para densificar rellenos heterogéneos y escombros, que pueden causar problemas a otras técnicas como las columnas de grava o las inclusiones rígidas. También se podría emplear para suelos finos cohesivos, sin embargo, el éxito en este caso es más dudoso, requiriendo atención la generación y disipación de las presiones intersticiales. En ocasiones, esta técnica se emplea de forma conjunta con las columnas de grava para facilitar la disipación de las presiones intersticiales (Bayuk y Walker, 1994).

Los patrones de caída suelen consistir en cuadrículas primarias y secundarias (y ocasionalmente terciarias), como las que se muestran en la Figura 3. Es habitual un espaciamiento entre puntos de impacto de 2 a 3 m en las mazas pequeñas y más de 10 m en el caso de mazas pesadas. Una vez que la profundidad del cráter alcanza aproximadamente 1 m, la abertura se rellena con material granular antes de proceder a nuevas caídas en ese lugar.

Figura 3. Fases en la compactación dinámica. Cortesía de Menard

El tratamiento se da en varias pasadas y la profundidad alcanzada por la densificación se puede relacionar con la energía del golpe mediante la siguiente fórmula empírica (Mayne et al, 1984):

donde:

M = masa de la maza (toneladas)

H = altura de caída (metros)

D = profundidad efectiva de la compactación (metros)

k = factor empírico que depende del tipo de suelo y de las características del tratamiento, que varía entre 0,35 (arenas limosas y limos con IP=10%) y 0,6 (gravas y arenas limpias), aunque un valor usual puede ser 0,5.

Teniendo en cuenta lo anterior, y conociendo las capacidades máximas de las grúas normalmente disponibles (H=30 m, M=20 t), la profundidad efectiva máxima varía entre 7 y 12 m, aproximadamente (Armijo y Blanco, 2017). No obstante, se pueden alcanzar profundidades de tratamiento de hasta 30 m (García Valcarce et al., 2003).

Durante la compactación existe un efecto instantáneo al reducirse el índice de huecos tras el impacto, y un efecto diferido en el caso de suelos saturados al disiparse la sobrepresión intersticial y reestructurarse el material a un estado más denso.

Con todo, la compactación dinámica presenta algunos inconvenientes. En efecto, se necesita una superficie mínima de 15000 m² para garantizar cierta rentabilidad económica y, además, se debe dejar una distancia mínima de 20 a 30 m a las estructuras próximas para evitar daños (García Valcarce et al., 2003).

El procedimiento de cómo se realiza la compactación dinámica está ampliamente descrito en el trabajo de Liausu (1984).

He grabado un pequeño vídeo explicativo de esta técnica de mejora de terrenos.

A continuación tenéis un folleto explicativo de Menard.

Descargar (PDF, 3.27MB)

Os dejo un vídeo explicativo del procedimiento constructivo que espero que os sea de interés.

Referencias

Armijo, G.; Blanco, M.A. (2017). Diseño y verificación del tratamiento de mejora del terreno mediante compactación dinámica. Aplicación a un caso real. https://www.interempresas.net/ObrasPublicas/Articulos/195230-Diseno-verificacion-tratamiento-mejora-terreno-mediante-compactacion-dinamica-Aplicacion.html
Bayuk, A.A.; Walker, A.D. (1994). “Dynamic Compaction. Two Case Histories Utilizing Innovative Techniques.” In-Situ Deep Soil Improvement, ASCE, Geotechnical Special Publication No.45.
Faraco, C. (1980). “Mejora del terreno de cimentación”, en Jiménez Salas (coord.) Geotecnia y Cimientos III, primera parte, pp. 489-531.
Findlay, J.D.; Sherwood, D.E. (1986).”Improvement of a hydraulic fill site in Bahrain using modified heavy tamping methods” Building on Marginal & Derelict Land., May 7-9.
García Valcarce, A. (dir.) (2003). Manual de edificación: mecánica de los terrenos y cimientos. CIE Inversiones Editoriales Dossat-2000 S.L. Madrid, 716 pp.
Liausu, P. (1984) Renforcement de Couches de Sol Compressibles par Substitution Dynamique, In-Situ Soil and Rock Reinforcement Conference, Paris.
Lundwall, N.B. (1968). The Saint George Temple, in “Temples of the Most High, Bookcraft, Salt Lake City, Chapter 3, p. 78.
Mayne, P.W.; Jones, J.S.; Dumas, J.C. (1984). Ground response to dynamic compaction. Journal of Geotechnical Engineering, ASCE, Vol. 110(6), pp. 757-774.
Ministerio de Fomento (2002). Guía de Cimentaciones. Dirección General de Carreteras.
Menard, L.; Broise Y. (1976). “Theoretical and practical aspects of dynamic consolidation”, Ground Treatment by deep compaction, Institution of Civil Engineers, LONDON, pp. 3-18.
Skempton, A.W. (1986). Standard Penetration Test Procedures and the Effects in Sand of Overburden Pressure, Relative Density, Particle Size, Ageing and Overconsolidation. Geotechnique, 36, pp. 425-437.
Uto, K.; Fuyuki, M. (1981). “Present and Future Trend on Penetration Testing in Japan”, Japanese Soc. SMFE.
Varaksin, S. (1981). “Recent development in soil improvement techniques and their practical applications”. Sol. Soils, Nº 38/39.
Yepes, V. (2020). Procedimientos de construcción de cimentaciones y estructuras de contención. Colección Manual de Referencia, 2ª edición. Editorial Universitat Politècnica de València, 480 pp. Ref. 328. ISBN: 978-84-9048-903-1.
Yepes, V. (2021). Procedimientos de construcción para la compactación y mejora del terreno. Colección Manual de Referencia, 1ª edición. Editorial Universitat Politècnica de València, 426 pp. Ref. 428. ISBN: 978-84-9048-603-0.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.