empuje de tierras – El blog de Víctor Yepes

¿Cómo evitar que nuestros muros deslicen?

Figura 1. Fuerzas que actúan sobre un muro.

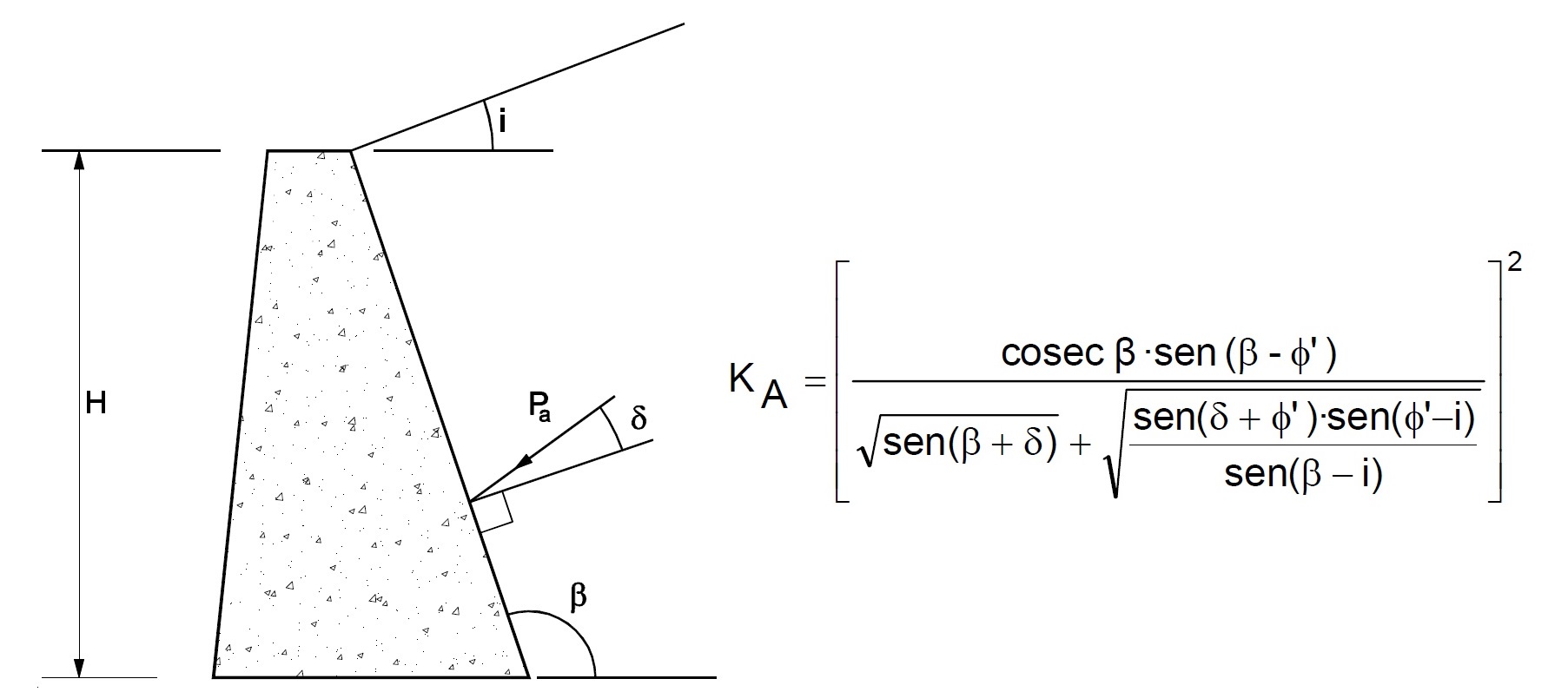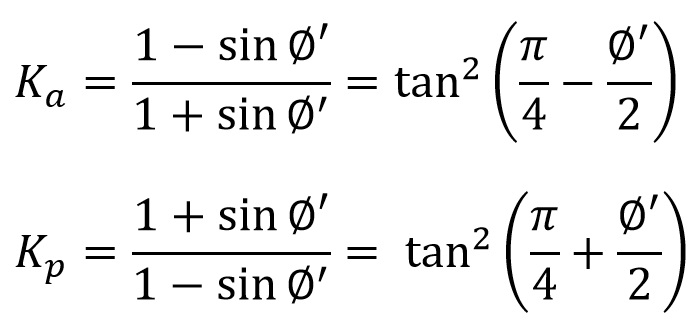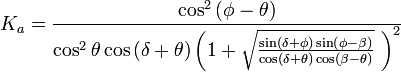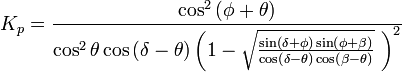
En un artículo anterior ya se comentó cómo el terreno empuja sobre cualquier estructura que lo contenga, y que la magnitud de dicho empuje se ve muy influenciada por el tipo de deformación sufrida por dicha estructura de contención, como puede ser un muro.

Lo inmediato es preguntar quién va a ser el responsable de contrarrestar dicho empuje para garantizar que el muro no deslice. No se trata de una cuestión menor, puesto que la seguridad al deslizamiento constituye uno de los estados límite últimos a comprobar cuando se diseña un muro. Es más, el deslizamiento acostumbra a ser el caso más crítico si el muro no es demasiado alto o en muros ménsula sin talón. Si a eso añadimos un mal drenaje en el trasdós cuando el muro no se ha calculado considerando los empujes hidrostáticos, tendremos asegurado un problema mayor.

Lo primero que se nos ocurre es pensar que el rozamiento entre el cimiento del muro y el terreno sobre el que se apoya debería ser suficiente para evitar el deslizamiento. De hecho, la fricción o fuerza de rozamiento que se opone al inicio del deslizamiento en un plano es proporcional a la fuerza normal a dicho plano, a través del conocido como coeficiente de rozamiento estático. Este coeficiente se puede calcular como la tangente del plano inclinado crítico, que es aquel donde un cuerpo empieza a deslizarse. Dicho coeficiente es mayor al coeficiente de rozamiento dinámico, que se desarrolla una vez el deslizamiento se ha iniciado.

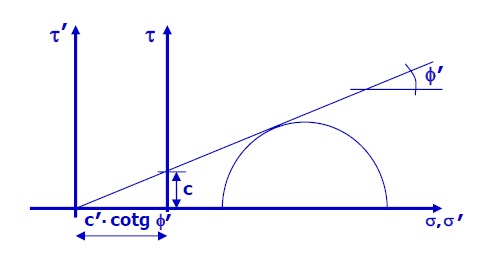
El caso del deslizamiento de un muro respecto al terreno es un caso parecido al de la rotura del suelo, pero teniendo en cuenta que las superficies en contacto son las del cimiento del muro y la del terreno sobre el que se apoya. Por tanto, se puede aplicar el criterio de rotura de Mohr-Coulomb, de forma que la tensión tangencial de rotura τ_rse encuentra relacionada con la tensión normal σ’ en el plano de contacto muro-terreno:

De forma análoga, se podría sustituir la cohesión entre partículas c‘ por un coeficiente de adherencia o cohesión de contacto c_c. Del mismo modo, se sustituiría el ángulo de rozamiento efectivo Φ‘ por el rozamiento muro-terreno Φ_c(siempre Φ_c <Φ‘ ). En este caso, siendo A el área de contacto de la fuerza normal con la superficie de deslizamiento, se puede expresar que la fuerza horizontal T en el plano de contacto muro-terreno sería:

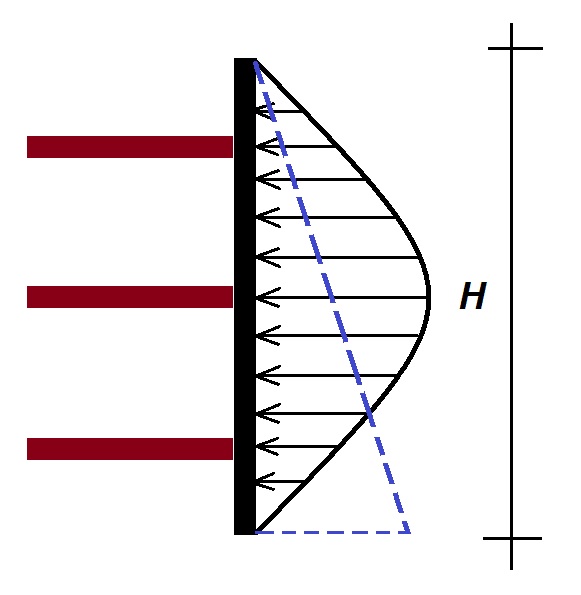
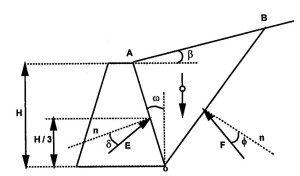
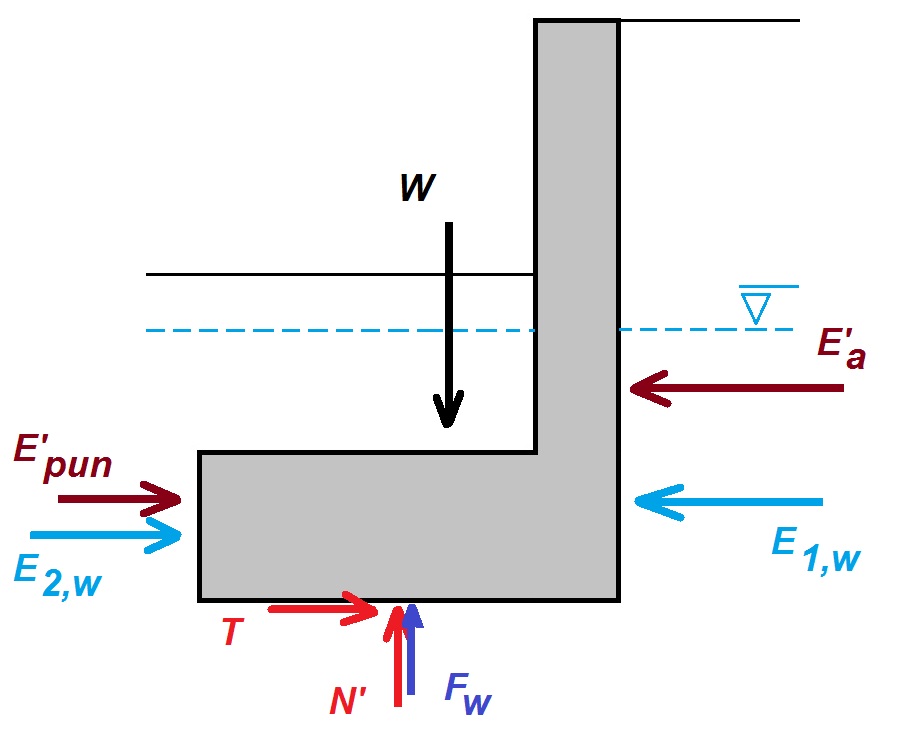
En la expresión anterior téngase en cuenta que la fuerza normal sobre la resultante N‘ es la diferencia entre la suma de las fuerzas verticales W y la subpresión ejercida por el agua F_w , en su caso (ver Figura 1).

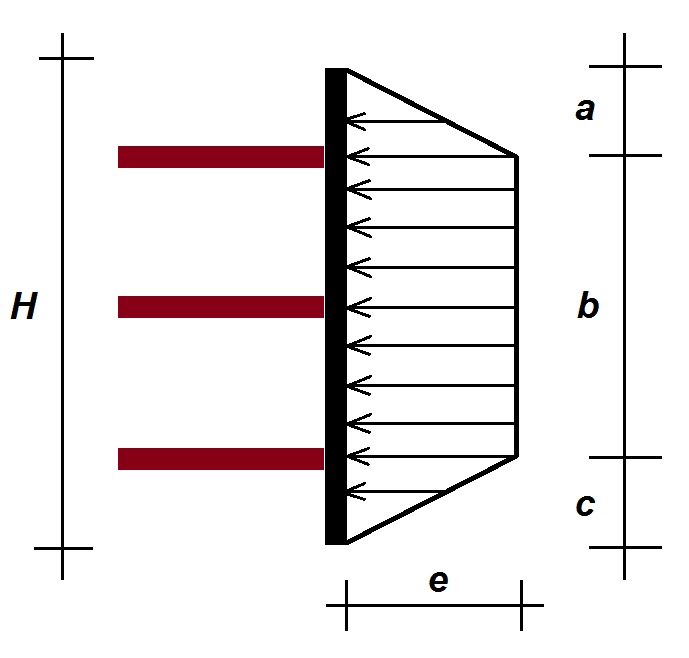
La fuerza horizontal T que se opone al deslizamiento es máxima en el instante mismo del deslizamiento. Si B‘ es el ancho eficaz de la zapata del muro en contacto con el terreno (no se tiene en cuenta la parte de la zapata “despegada” del terreno, ver Figura 2), la fuerza horizontal máxima T_máx que se opondrá al deslizamiento por metro lineal de muro sería la siguiente:

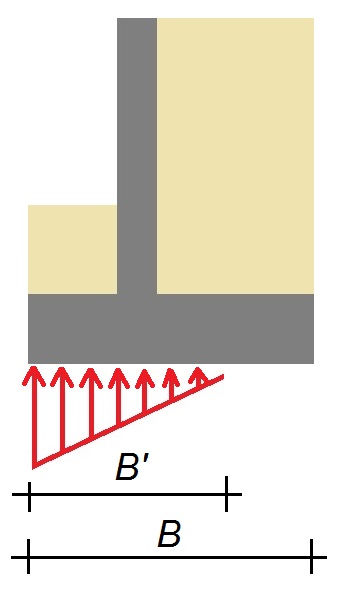
Si esta fuerza horizontal máxima T_máx no fuese suficiente para equilibrar las fuerzas horizontales sobre el muro (E’_a + E_1,w ), entonces se tendría que recurrir a una resistencia adicional R que puede proceder de la movilización de una parte del empuje pasivo que actúa sobre la puntera de la zapata del muro E’_pun , del posible empuje hidrostático sobre la puntera E_2,w o bien de posibles fuerzas exteriores al sistema muro-terreno. Se recomienda que R ≤ 0,10·H , siendo H la fuerza horizontal.

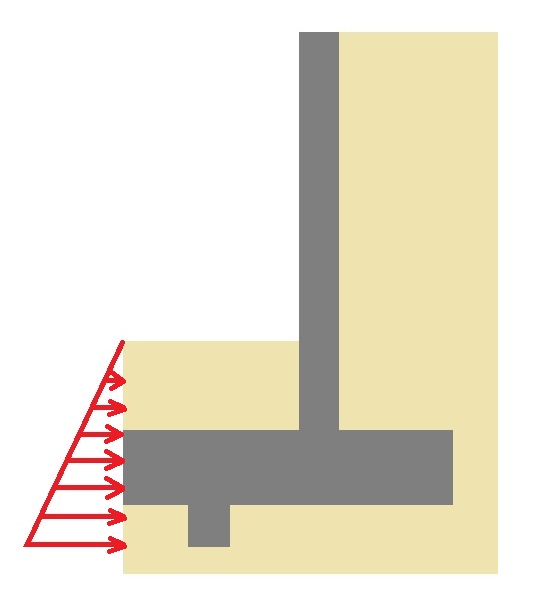
Además, en el caso de tenerse en cuenta el empuje pasivo efectivo sobre la puntera (o bien sobre una zarpa o tacón de la zapata, para incrementar dicho empuje pasivo, ver Figura 3) hay que garantizar que se moviliza la deformación suficiente y que su valor se debe minorar por un coeficiente de 1,5, que sería E’_{p admisible}. Por otra parte, si se tiene en cuenta dicho empuje pasivo , se debería garantizar la permanencia del terreno sobre la zapata. Está del lado de la seguridad no considerar el empuje pasivo.

Figura 3. Aumento del empuje pasivo debido al tacón en la zapata del muro.

Todo lo anterior nos hace reflexionar sobre la importancia de definir en el proyecto del muro los parámetros resistentes del contacto muro-terreno. Dependiendo de la forma de preparación del contacto, se pueden considerar los siguientes:

Muros de hormigón ejecutados “in situ” contra el terreno → tan Φ_c= 0,8·tan Φ‘ y c_c = c‘
Muros de hormigón prefabricado sobre materiales granulares → tan Φ_c= 0,6 y c_c = 0
Muros sobre suelos arcillosos saturados: Hay que comprobar la situación de corto plazo → Φ_u = 0 y c_u = 0,5 · R_u (siendo R_u la resistencia a compresión simple sin drenaje)

A falta de otros datos, se adopta como ángulo de rozamiento muro-terreno un valor de 2/3 del ángulo de rozamiento efectivo del terreno, es decir, Φ_c= 2/3 · Φ‘ . Es decir, siempre será el ángulo de rozamiento muro-terreno inferior al ángulo de rozamiento efectivo del terreno.

Por último, tendríamos que asignar un coeficiente de seguridad al deslizamiento F_d, como el cociente entre la máxima oposición que puede encontrar el muro al deslizamiento (T_máx +E’_{p admisible}) entre la fuerza estrictamente necesaria para evitarlo ( T_nec ). La fuerza estrictamente necesaria para evitar el deslizamiento debe ser la suma de fuerzas horizontales sobre el muro, incluido el empuje activo del terreno y posible la presión hidrostática sobre el trasdós del muro.

En combinación de acciones casi permanente, la “Guía de cimentaciones en obras de carretera” (Ministerio de Fomento, 2003), establece un coeficiente de seguridad frente al deslizamiento mínimo de 1,50.

REFERENCIAS:

IZQUIERDO, F.A. (2001). Cuestiones de geotecnia y cimientos. Editorial Universidad Politécnica de Valencia, 227 pp.
MINISTERIO DE FOMENTO (2002). Guía de Cimentaciones. Dirección General de Carreteras.
YEPES, V. (2020). Procedimientos de construcción de cimentaciones y estructuras de contención. Colección Manual de Referencia, 2ª edición. Editorial Universitat Politècnica de València, 480 pp. Ref. 328. ISBN: 978-84-9048-903-1.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Empujes sobre entibaciones según Terzaghi y Peck

Figura 1. Entibación en excavación de zanja. https://commons.wikimedia.org/wiki/File:Sbh_s600.JPG

Ya se habló en un artículo anterior de la altura crítica, que si se sobrepasa, obliga a entibar una excavación. Este es un aspecto de gran importancia en la seguridad de las personas. Para ello resulta fundamental el cálculo de los empujes del terreno sobre la entibación para dimensionar correctamente los elementos constitutivos de esta estructura auxiliar.

La deformación que se desarrolla en el terreno al ir entibando una excavación, poniendo puntales de arriba hacia abajo, es diferente a la que desarrollan la condición de empuje activo en los muros. Este hecho provoca que la distribución real de los empujes sobre una entibación sea diferente a la clásica ley triangular que aparecen en los muros. Esto se debe, entre otros motivos, a que la entibación va a girar respecto a un punto situado en la parte superior (primer apuntalamiento), frente al típico muro en ménsula, donde el giro se realiza, aproximadamente, en la base de la estructura.

En la Figura 2 podemos ver que los empujes reales no crecen proporcionalmente con la profundidad y que, en el fondo de la excavación, acaban anulándose. Por tanto, la parte superior, que se apuntala desde el primer momento, recibe unos empujes superiores a los de la ley triangular, y en la parte inferior, son menores. La ley de empujes, por tanto, se aproxima a una parábola.

Figura 2. Empujes reales de forma parabólica sobre entibaciones

Terzaghi y Peck (1967) propusieron algunos esquemas simplificados útiles para determinados suelos típicos. Son los denominados “diagramas de presión aparente“, deducidos a partir de medidas realizadas en diferentes obras a mediados del siglo XX (Berlín, Múnich, Chicago, Nueva York y Oslo) en entibaciones apuntadas, no ancladas, de más de 6 m de profundidad. No se trata realmente de unos diagramas de empujes únicos, sino de las envolventes empíricas de los distintos diagramas reales que se observan en una fase de excavación y que pueden ser bastante complicados (secuencia de construcción, temperatura, acomodo entre pantalla y apoyos, etc.).

Teniendo en cuanto los valores a, b y c de la Figura 3, se pueden estimar la ley de empujes en función de la Tabla 1 (Izquierdo, 2001). Hay que tener presente que estos empujes, sacados de mediciones realmente tomadas en obra, son aplicables a los empujes sobre entibaciones, por lo que no es de aplicación directa a superficies continuas y mucho más rígidas como los muros pantalla.

Figura 3. Distribuciones propuestas para empuje sobre entibaciones

Tabla 1. Procedimiento empírico de Terzaghi y Peck (1967) para determinar las cargas sobre los puntales en una excavación entibada (Izquierdo, 2001)

En la Tabla 1, K_a es el coeficiente de empuje activo, c_u la cohesión del terreno sin drenaje y γ su peso específico.

REFERENCIAS:

GARCÍA VALCARCE, A. (dir.) (2003). Manual de edificación: mecánica de los terrenos y cimientos. CIE Inversiones Editoriales Dossat-2000 S.L. Madrid, 716 pp.
GONZÁLEZ CABALLERO, M. (2001). El terreno. Edicions UPC, Barcelona, 309 pp.
IZQUIERDO, F.A. (2001). Cuestiones de geotecnia y cimientos. Editorial Universidad Politécnica de Valencia, 227 pp.
LAMBE, T.W.; WHITMAN, R.V. (1996). Mecánica de suelos. Limusa, México, D.F., 582 pp.
MINISTERIO DE FOMENTO (2002). Guía de Cimentaciones. Dirección General de Carreteras.
MINISTERIO DE LA VIVIENDA (2006). Código Técnico de la Edificación
TERZAGHI, K.; PECK, R. (1967). Soil Mechanics in Engineering Practice. 2nd Edition, John Wiley, New York.
YEPES, V. (2020). Procedimientos de construcción de cimentaciones y estructuras de contención. Colección Manual de Referencia, 2ª edición. Editorial Universitat Politècnica de València, 480 pp. Ref. 328. ISBN: 978-84-9048-903-1.
YEPES, V. (2023). Maquinaria y procedimientos de construcción. Problemas resueltos. Colección Académica. Editorial Universitat Politècnica de València, 562 pp. Ref. 376. ISBN 978-84-1396-174-3
YEPES, V. (2024). Estructuras auxiliares en la construcción: Andamios, apeos, entibaciones, encofrados y cimbras. Colección Manual de Referencia, serie Ingeniería Civil. Editorial Universitat Politècnica de València, 408 pp. Ref. 477. ISBN: 978-84-1396-238-2

Cursos:

Curso de estructuras auxiliares en la construcción: andamios, apeos, entibaciones, encofrados y cimbras.

Curso de Procedimientos de Construcción de cimentaciones y estructuras de contención en obra civil y edificación.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Empuje de tierras, ¿mejor Coulomb o Rankine?

Figura 1. Coulomb y Rankine, autores de dos de los modelos clásicos de empuje de tierras.

El empuje de tierras sobre estructuras de contención ha sido un problema clásico en Geotecnia, pero que es complejo, pues existen numerosas incertidumbres asociadas al comportamiento de los distintos tipos de terreno. Tanto la dificultad en la determinación de las características mecánicas d

el terreno real como la complejidad en las hipótesis de cálculo han llevado a la utilización de simplificaciones útiles en una gran mayoría de casos. Las dos teorías clásicas en la estimación de los empujes del terreno se deben al francés Charles-Agustin de Coulomb (1736-1806) y al escocés William John Macquorn Rankine (1820-1872). Ambos métodos se sustentan en hipótesis diferentes y los resultados que proporcionan no coinciden, salvo en algún caso muy particular.

En cualquier libro de Geotecnia se puede comprobar cómo integrando las ecuaciones diferenciales de las condiciones de equilibrio interno de un elemento diferencial de un terreno horizontal, homogéneo, isótropo y con un comportamiento elástico, la tensión horizontal depende de la vertical. En el caso de que el terreno estuviera confinado lateralmente, con deformación lateral nula, la ley de Hooke proporciona una solución al problema, siendo la relación entre la tensión horizontal y la vertical constante. En cualquier caso, la condición de utilizar una ley de esfuerzo-deformación conveniente constituye el mayor obstáculo para obtener una solución exacta al problema.

Las presiones que soporta un muro o una pantalla reciben el nombre de empujes, que en el caso más general, será la suma del empuje hidrostático más el empuje efectivo ejercido por las partículas del terreno. Se define el coeficiente de empuje como la relación entre la tensión efectiva horizontal y la vertical, y en el caso de que no exista deformación lateral, se denomina coeficiente de empuje al reposo, K₀. De esta forma se podría calcular el empuje sobre un muro que no se deformara lo más mínimo. Sería el caso de un muro de sótano en edificación. Pero los muros no son infinitamente rígidos, se deforman, y dependiendo de si la deformación lateral es negativa (el terreno “se descomprime”) o positiva (el terreno “se comprime”), tendríamos los denominados empujes activos K_a, o pasivos K_p, (K_a<K₀<K_p). Para movilizar el empuje pasivo son necesarios movimientos del muro contra el terreno muy superiores a los necesarios para llegar a una situación de empuje activo. Cuando el empuje pasivo es favorable, debido a la imprecisión en la determinación de su valor real, por seguridad suele despreciarse su efecto o bien se aplica un coeficiente reductor (por ejemplo, de 1,5). Dejamos al lector investigar sobre este asunto en la literatura habitual.

Figura 2. Relación entre empuje del terreno y los movimientos necesarios para su desarrollo (Código Técnico de Edificación)

Lo que nos interesa en esta entrada es conocer las diferencias entre el método de Coulomb y el de Rankine e intentar interpretar cuándo sería mejor utilizar uno u otro método. Las fórmulas se pueden deducir de cualquier libro o manual de geotecnia. En ambos casos se puede generalizar la formulación al caso de terrenos cohesivos, presencia de nivel freático, cargas uniformes sobre el trasdós e inclinación del relleno tras el muro. Siendo σ’_v es la tensión efectiva vertical y c‘ la cohesión efectiva del terreno o relleno del trasdós, el empuje activo P_ase define como la resultante de los empujes unitarios σ’_a que puede determinarse mediante la siguiente fórmula:

y de forma análoga, el empuje pasivo P_p se define como la resultante de los empujes unitarios σ’_p que puede determinarse mediante:

La cohesión es un aspecto favorable para disminuir el empuje del terreno, pero si al final no se acaba desarrollando, nos deja del lado de la inseguridad; por tanto, como a veces es difícil estimar su efecto de forma adecuada, es habitual despreciarla para quedar del lado de la seguridad. Por tanto, se aconseja ser muy cuidadoso a la hora de considerar la cohesión.

Coulomb propuso un modelo para estimar los empujes del terreno planteando el equilibrio de una masa de terreno en forma de cuña al deformarse o moverse el muro. La rotura se produce a lo largo de dos planos, el formado por el interface suelo-muro y el plano de deslizamiento en el terreno. La cuña, formada por los dos planos, se comporta como un bloque rígido. De todas las cuñas posibles, una es la que produce el empuje activo máximo, y ese es el problema resuelto por este ingeniero francés en 1776. El método supone que las superficies de deslizamiento son planas, pero esta hipótesis es muy discutible en el caso del empuje pasivo. El problema queda resuelto para un muro cualquiera, con un trasdós que no necesita ser vertical, y un terreno con una determinada inclinación y con unas cargas sobre su superficie. Se supone conocido el peso específico del terreno, el ángulo de rozamiento interno y el ángulo de rozamiento muro-suelo. Es actualmente el método más empleado para el diseño de muros por métodos de equilibrio límite. Hoy día se emplea con gran efectividad en el cálculo de muros de gravedad, lo que permite considerables ahorros de material. Las fórmulas que siguen indican los coeficientes de empuje activo y pasivo, con las figuras que definen cada uno de los ángulos correspondientes:

El método de Rankine (1857) es más elegante desde el punto de vista matemático, explicando el empuje en términos de rotura por cortante del terreno. Se obtienen los empujes partiendo de un semiespacio infinito que se encuentra en “estado de Rankine“, es decir, un estado de equilibrio plástico y en donde el muro no produce ninguna perturbación. Se supone que el terreno es homogéneo e isótropo y en estado de equilibrio plástico, es decir, se acepta que toda la masa en el trasdós del muro está en situación de rotura y, por tanto, en cualquier punto el estado tensional pertenece a un círculo de Morh que es tangente a la línea de rotura de este suelo; además, como hipótesis adicional, no hay variación de tensiones en los puntos de cualquier plano paralelo a la superficie del semiespacio. Este modelo puede resultar un tanto conservador, pues solo considera el ángulo de rozamiento interno del terreno, olvidando el efecto favorable del rozamiento entre el muro y el terreno. Este método tiene muchas aplicaciones prácticas, por ejemplo, en muros ménsula, donde la suposición de Rankine no supone grandes desventajas y simplifica enormemente los cálculos. El cálculo de empujes sobre un muro con el modelo de Rankine se reduce a obtener las presiones efectivas a la profundidad correspondientes y aplicar las fórmulas correspondientes. De esta forma es muy sencillo calcular terrenos estratificados y considerar la existencia de una carga uniforme en coronación. Además, el método permite estimar si existen grietas de tracción y su profundidad en un terreno que sea cohesivo. Los coeficientes de empuje activo y pasivo para un terreno que forma un ángulo i con la horizontal teniendo en cuenta que la resultante forma un ángulo i con la horizontal, son los siguientes:

Aplicando el teorema de los estados correspondientes de Caquot, se puede generalizar la teoría de Rankine a suelos cohesivos: “Si a un suelo con cohesión que está en situación límite de rotura, simultáneamente le quitamos la cohesión y sumamos a todas las tensiones un término (c’ · cotg Φ’), el suelo sigue estando en la misma situación límite de rotura” (y se le aplican las hipótesis de los suelos sin cohesión).

Figura 3. Círculo de Mohr considerando suelos cohesivos

De las fórmulas deducidas para el empuje activo y pasivo, las fórmulas en ambos modelos coinciden únicamente en el caso de un trasdós vertical del muro, no hay rozamiento suelo-estructura y la superficie del terreno es horizontal. En este caso, los coeficientes de empuje activo y pasivo son los siguientes:

Resumiendo los aspectos básicos expuestos anteriormente, podríamos decir lo siguiente:

En caso de terrenos estratificados, la inclinación del plano de deslizamiento depende de cada terreno, con lo que el problema puede ser indeterminado si utilizamos el modelo de Coulomb. En este caso, Rankine es de más fácil formulación, que suele ser recomendable en el caso de muros ménsula.
El método de Coulomb no tiene en cuenta la presencia de grietas de tracción, por lo que con terrenos cohesivos el cálculo de la profundidad de estas grietas se debe hacer con Rankine.
Si no existe cohesión en el terreno ni adherencia entre muro y terreno, con la teoría de Coulomb se puede determinar que la resultante del empuje activo está situada, desde la base del muro, a un tercio de la altura del muro. Si no es así, entonces el método no proporciona directamente la posición del empuje.
El método de Rankine es difícil de aplicar con geometrías mínimamente complejas (trasdós quebrado, superficies del terreno en el trasdós no planas, cargar arbitrarias sobre éste último) y no es mucho más preciso que el método de Coulomb para estos casos.
El método de Coulomb no estima bien el empuje pasivo, pues la superficie real de rotura no es plana (se asemeja a una espiral logarítmica) y la distribución de empujes difiere bastante de la triangular, proporcionando valores sobredimensionados (del lado de la inseguridad). El método de Rankine es más conservador para el cálculo de empujes pasivos.
El método de Rankine no considera el rozamiento entre el muro y el terreno, lo cual es conservador. Es un aspecto importante en muros de gravedad, cuyos empujes activos se prefieren calcular con Coulomb.
En el método de Coulomb permite la consideración de sobrecargas en el trasdós de cualquier tipo (constante, puntual, triangular, etc.) siempre que sean indefinidas en el sentido longitudinal del muro, pues basta introducirlas en las ecuaciones de equilibrio. Con Rankine es sencillo si se trata de una sobrecarga constante.

REFERENCIAS:

GARCÍA VALCARCE, A. (dir.) (2003). Manual de edificación: mecánica de los terrenos y cimientos. CIE Inversiones Editoriales Dossat-2000 S.L. Madrid, 716 pp.
GONZÁLEZ CABALLERO, M. (2001). El terreno. Edicions UPC, Barcelona, 309 pp.
IZQUIERDO, F.A. (2001). Cuestiones de geotecnia y cimientos. Editorial Universidad Politécnica de Valencia, 227 pp.
LAMBE, T.W.; WHITMAN, R.V. (1996). Mecánica de suelos. Limusa, México, D.F., 582 pp.
MINISTERIO DE FOMENTO (2002). Guía de Cimentaciones. Dirección General de Carreteras.
MINISTERIO DE LA VIVIENDA (2006). Código Técnico de la Edificación
YEPES, V. (2020). Procedimientos de construcción de cimentaciones y estructuras de contención. Colección Manual de Referencia, 2ª edición. Editorial Universitat Politècnica de València, 480 pp. Ref. 328. ISBN: 978-84-9048-903-1.
YEPES, V. (2023). Maquinaria y procedimientos de construcción. Problemas resueltos. Colección Académica. Editorial Universitat Politècnica de València, 562 pp. Ref. 376. ISBN 978-84-1396-174-3

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Laboratorio virtual: empuje de tierras sobre un muro según Coulomb

El ingeniero militar francés Charles-Augustin de Coulomb (1776) fue el primero en estudiar el problema de las presiones laterales del terreno y estructuras de retención. Este autor introduce una simplificación importante para calcular el empuje: se limitó a usar la teoría de equilibrio que considera que una cuña de terreno en rotura imitada por el trasdós y por un plano que pasa por el pie del muro como un cuerpo en movimiento para determinar la presión lateral limitante. La presión limitante horizontal en fallo en extensión o compresión se determinan a partir de K_a y K_p respectivamente. Se supone que la superficie de deslizamiento es plana, el drenaje del muro funciona bien y que no hay presiones intersticiales en el terreno. Aunque con simplificaciones, esta teoría permite calcular problemas en los cuales el paramento no es vertical y la superficie de relleno tiene cualquier forma.

$K_a = frac{ cos ^2 left( phi - theta right)}{cos ^2 theta cos left( delta + theta right) left( 1 + sqrt{ frac{ sin left( delta + phi right) sin left( phi - beta right)}{cos left( delta + theta right) cos left( beta - theta right)}} right) ^2}$

$K_p = frac{ cos ^2 left( phi + theta right)}{cos ^2 theta cos left( delta - theta right) left( 1 - sqrt{ frac{ sin left( delta + phi right) sin left( phi + beta right)}{cos left( delta - theta right) cos left( beta - theta right)}} right) ^2}$

Para que se pueda estudiar de forma cualitativa el efecto del empuje, se aporta un Laboratorio Virtual. El objetivo de este objeto de aprendizaje consiste en entender cómo varía el empuje activo horizontal sobre un muro aplicando la teoría de Coulomb. Éste coeficiente varía en función del ángulo de rozamiento interno del terreno, del ángulo de rozamiento de terreno y muro, y de la inclinación del muro. Supondremos un relleno horizontal sobre el muro.

Enlace al laboratorio virtual: https://laboratoriosvirtuales.upv.es/eslabon/EmpujeHorizontal/

Referencias:

Coulomb C.A., (1776). Essai sur une application des regles des maximis et minimis a quelques problemes de statique relatifs a l’architecture. Memoires de l’Academie Royale pres Divers Savants, Vol. 7

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

¿Cómo evitar accidentes por enterramiento en zanjas?

Una de las unidades de obra que más vidas se cobra es la excavación de zanjas. Se entiende por zanja una excavación larga y angosta realizada en el terreno. En los trabajos llevados a cabo en zanjas se producen con frecuencia accidentes graves o mortales a causa del desprendimiento de tierras. Por ello es necesario adoptar aquellas medidas que garanticen la seguridad de los trabajadores que tienen que llevar a cabo labores en el interior de las mismas . Con carácter general se deberá considerar peligrosa toda excavación que, en terrenos corrientes, alcance una profundidad de 0,80 m y 1,30 m en terrenos consistentes. Un buen monográfico al respecto es el elaborado por el Instituto Vasco de Seguridad y Salud Laborales, o este otro del Instituto Regional de Seguridad y Salud en el Empleo, de la Comunidad de Madrid. Por su interés, os recomiendo que os lo estudiéis atentamente.

Evidentemente, con una buena entibación y el buen juicio y la prudencia de las personas se pueden evitar muchos problemas. Aunque a veces, es suficiente con bermas y taludes adecuados. El desmoronamiento de una zanja afecta gravemente a la seguridad de los operarios que trabajan en ella. Para evitar accidentes es importante conocer el empuje de tierras a los que se somete una entibación para evitar su colapso. Con el objetivo de ayudar a entender de forma cualitativa a nuestros alumnos el comportamiento de la presión a la que está sometida una entibación en función del peso específico y ángulo de rozamiento interno del terreno y la profundidad a la que se encuentra dicha entibación, en la Universitat Politècnica de València se han desarrollado unos objetos de aprendizaje que permiten visualizar dicho comportamiento. Con todo, existen causas más importantes incluso que provocan el desmoronamiento de una zanja como es la heterogeneidad del terreno, la presencia de elementos intermedios (canalizaciones, etc), las acciones de agentes externos (trafico rodado, acopios) y las inclemencias del tiempo y condiciones climáticas. Por tanto, el modelo que os pasamos es, evidentemente, demasiado sencillo, pero permite una primera llamada de atención ante este grave problema. Como siempre, la experiencia y el buen juicio del responsable de la obra y de los operarios está por encima de cualquier otra consideración. Os paso a continuación este pequeño objeto de aprendizaje.

La forma de trabajar con ellos es muy sencilla. Se debe seleccionar: la profundidad de la zanja (valores entre 1 y 15 m), peso específico aparente del terreno (hasta 30 kN/m3) y ángulo de rozamiento interno del terreno (en grados sexagesimales, hasta un valor de 60º). No se admiten valores negativos. Espero que os guste. El enlace es: https://laboratoriosvirtuales.upv.es/eslabon/Entibacion/

Además, os paso varios vídeos al respecto. Espero que os sean de utilidad.

Referencia:

YEPES, V. (2020). Procedimientos de construcción de cimentaciones y estructuras de contención. Colección Manual de Referencia, 2ª edición. Editorial Universitat Politècnica de València, 480 pp. Ref. 328. ISBN: 978-84-9048-903-1.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.