laboratorio virtual – El blog de Víctor Yepes

Propiedades de las clotoides

http://arablogs.catedu.es/blog.php?id_blog=1535&id_articulo=182544

Seguimos con este post viendo ejemplos de Laboratorios Virtuales de la Universitat Politècnica de València como herramienta innovadora para la docencia universitaria. Se trata de un laboratorio desarrollado por los profesores de la Unidad Docente de Caminos y Aeropuertos de la Universitat Politècnica de València, los profesores Francisco Javier Camacho Torregrosa, Ana María Pérez Zuriaga y Alfredo García García, donde se visualizan las propiedades de las clotoides.

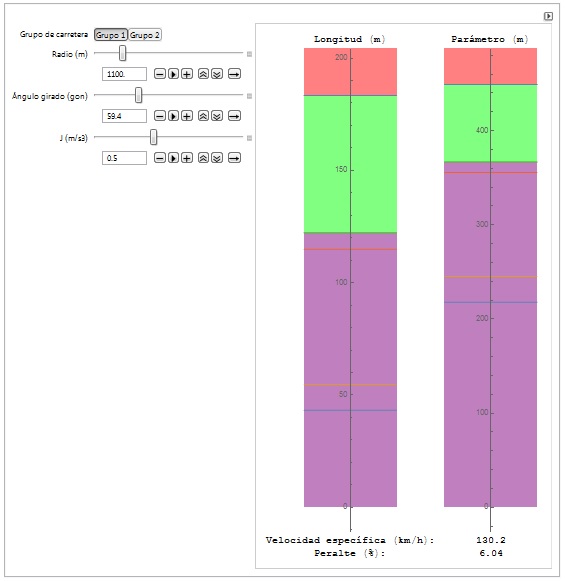
Este objeto muestra al usuario el rango de parámetros y longitudes válidos para el diseño de curvas de transición, de acuerdo con la Instrucción de Trazado 3.1 IC. El laboratorio mostrará la longitud mínima obligatoria del diseño, así como el resto de criterios. En verde mostrará el rango válido, mientras que en naranja (en su caso) se muestran los parámetros y longitudes que cumplen con los criterios obligatorios pero no con el recomendable.

Instrucciones

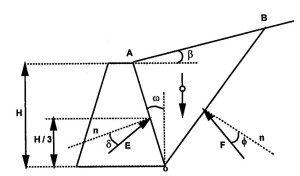
El usuario deberá introducir parámetros básicos del diseño, tales como el tipo de carretera, radio y el ángulo de giro de la curva, así como la variación de la aceleración centrífuga (J). El valor de este último parámetro debe ser siempre el mínimo, salvo casos justificados.

El enlace al laboratorio virtual es el siguiente: http://labmathematica.upvnet.upv.es/eslabon/Ejercicio.asp?do=LongitudClotoid

NOTA: Para poder ver los laboratorios necesita el plugin del Wolfram CDF Player. Si no lo tiene instalado en su equipo, puede descargarlo en la página web de Wolfram. Si utiliza un equipo público o no dispone de privilegios para instalar software, puede visualizar el laboratorio desde un servidor remoto. Tan sólo necesitará que su navegador incluya soporte para aplicaciones Java. Pulse aquí para visualizar el laboratorio sin instalar el plugin de Mathematica CDF Player

Este obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Laboratorio virtual: empuje de tierras sobre un muro según Coulomb

El ingeniero militar francés Charles-Augustin de Coulomb (1776) fue el primero en estudiar el problema de las presiones laterales del terreno y estructuras de retención. Este autor introduce una simplificación importante para calcular el empuje: se limitó a usar la teoría de equilibrio que considera que una cuña de terreno en rotura imitada por el trasdós y por un plano que pasa por el pie del muro como un cuerpo en movimiento para determinar la presión lateral limitante. La presión limitante horizontal en fallo en extensión o compresión se determinan a partir de K_a y K_p respectivamente. Se supone que la superficie de deslizamiento es plana, el drenaje del muro funciona bien y que no hay presiones intersticiales en el terreno. Aunque con simplificaciones, esta teoría permite calcular problemas en los cuales el paramento no es vertical y la superficie de relleno tiene cualquier forma.

$K_a = frac{ cos ^2 left( phi - theta right)}{cos ^2 theta cos left( delta + theta right) left( 1 + sqrt{ frac{ sin left( delta + phi right) sin left( phi - beta right)}{cos left( delta + theta right) cos left( beta - theta right)}} right) ^2}$

$K_p = frac{ cos ^2 left( phi + theta right)}{cos ^2 theta cos left( delta - theta right) left( 1 - sqrt{ frac{ sin left( delta + phi right) sin left( phi + beta right)}{cos left( delta - theta right) cos left( beta - theta right)}} right) ^2}$

Para que se pueda estudiar de forma cualitativa el efecto del empuje, se aporta un Laboratorio Virtual. El objetivo de este objeto de aprendizaje consiste en entender cómo varía el empuje activo horizontal sobre un muro aplicando la teoría de Coulomb. Éste coeficiente varía en función del ángulo de rozamiento interno del terreno, del ángulo de rozamiento de terreno y muro, y de la inclinación del muro. Supondremos un relleno horizontal sobre el muro.

Enlace al laboratorio virtual: https://laboratoriosvirtuales.upv.es/eslabon/EmpujeHorizontal/

Referencias:

Coulomb C.A., (1776). Essai sur une application des regles des maximis et minimis a quelques problemes de statique relatifs a l’architecture. Memoires de l’Academie Royale pres Divers Savants, Vol. 7

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Laboratorio virtual: peso específico de un suelo

Se entiende por suelo al seudosólido formado por un conjunto de partículas sólidas que forman una estructura en cuyo seno existen huecos ocupados por agua y aire en proporciones variables. El “peso específico de un suelo“, como relación entre el peso y su volumen, es un valor dependiente de la humedad, de los huecos de aire y del peso específico de las partículas sólidas. Para evitar confusiones, las determinaciones de los ensayos de laboratorio facilitan por un lado el “peso específico seco” y por otro la humedad. Fijémonos que este término es diferente de la “densidad del suelo“, que establece una relación entre la masa y el volumen. También suele utilizarse un valor adimensional denominado, “peso especifico relativo”, definido como el cociente entre el peso específico del suelo y el peso específico del agua a una temperatura determinada. Los valores típicos de gravedades específicas para los sólidos del suelo son entre 2.65 y 2.72. En la figura que sigue se observan los componentes de un suelo, con las notaciones sobre sus pesos y volúmenes, lo cual permite definir parámetros que caracterizan el estado físico de dicho suelo.

Estos conceptos son básicos y muy conocidos para el alumno de un curso de geotecnia en un grado de ingeniería civil. Sin embargo, para facilitar el proceso de aprendizaje os facilito a continuación un enlace a un pequeño laboratorio virtual donde el alumno puede comprobar por sí mismo cómo varía el peso específico seco en función de la humedad y del peso específico de las partículas sólidas. Las instrucciones son muy sencillas: se debe seleccionar el rango máximo para la humedad y el contenido de huecos de aire, en tanto por cien, con valores comprendidos entre 0 y 100; además se seleccionará el peso específico de las partículas sólidas en kN/m3. No se admiten valores negativos.

El enlace a dicho laboratorio virtual es: https://laboratoriosvirtuales.upv.es/eslabon/DensidadSuelo/

Referencias:

YEPES, V. (2014). Equipos de compactación superficial. Apuntes de la Universitat Politècnica de València, Ref. 187. Valencia, 113 pp.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Diagrama de peraltes para curvas en ‘S’ en carreteras de calzada única.

En este post voy a enseñaros una herramienta muy interesante desde el punto de vista docente. Se trata de los Laboratorios Virtuales. Los alumnos pueden interactuar en línea para aprender. En este caso os paso uno desarrollado por los profesores de la Unidad Docente de Caminos y Aeropuertos de la Universitat Politècnica de València, los profesores Francisco Javier Camacho Torregrosa, Ana María Pérez Zuriaga y Alfredo García García.

En este laboratorio se aborda el diseño de la transición del peralte entre curvas en planta de diferente sentido de giro. Existen dos posibles formas de realizar la transición del peralte, en función de la longitud de la recta intermedia. En caso de que la recta intermedia sea suficientemente larga, se dispondrá bombeo en la misma, para lo cual se realizará la transición del peralte y del desvanecimiento del bombeo propio de las curvas aisladas. En el caso de que la longitud de la recta intermedia sea insuficiente (menor de 150 m en carreteras del grupo 2 y 300 m en carreteras del grupo 1), la transición del peralte se realizará por medio de la comúnmente llamada ‘pajarita’, que impone un cambio rápido de peralte en la zona central, no existiendo bombeo en dicha recta. En el tramo circular de las curvas en planta se mantendrá el peralte constante en todo momento. Los objetivos de este laboratorio virtual son: Identificar la influencia de los diferentes parámetros que forman parte del diseño de acuerdos de carreteras. Y representar el perfil longitudinal de una carretera a la escala adecuada (10H:1V). Continue reading “Diagrama de peraltes para curvas en ‘S’ en carreteras de calzada única.” →

¿Cómo varía la trayectoria de una carga sobre un cable?

En el artículo de hoy vamos a dar un ejemplo de una herramienta que se denomina “laboratorio virtual” y que se usa como objeto de aprendizaje en la Universidad Politécnica de Valencia. Consiste en un pequeño programa en línea que sirve a nuestros alumnos para aprender a visualizar cómo varían las magnitudes de un problema en función de las variables de entrada. Evidentemente es algo muy sencillo, pero pienso que práctico cuando se quiere potenciar el conocimiento explicativo de los estudiantes.

En el caso que os presento, se trata de conocer cómo varía la trayectoria de una carga que se desplaza sobre un cable, lo cual es útil en la definición de gálibos y cálculo de la tensión máxima en el cable basándose en las coordenadas de un punto conocido de la misma. Se denomina flecha a la distancia entre la recta que une los apoyos y el cable. Basta que pinchéis sobre el cuadro “dibujar” para ver los resultados.

El enlace es el siguiente: https://laboratoriosvirtuales.upv.es/eslabon/Cable/

Referencias:

YEPES, V.; MARTÍ, J.V. (2017). Máquinas, cables y grúas empleados en la construcción. Editorial de la Universitat Politècnica de València. Ref. 814. Valencia, 210 pp.