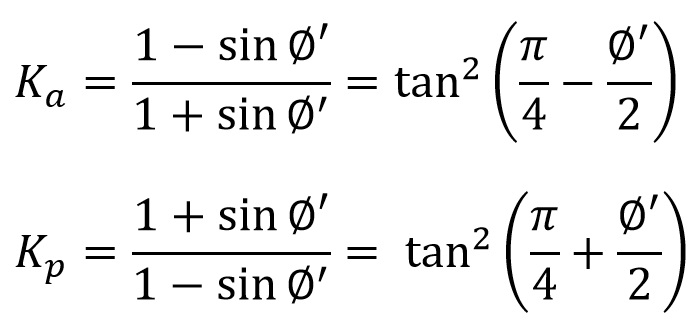El empuje de tierras sobre estructuras de contención ha sido un problema clásico en Geotecnia, pero que es complejo, pues existen numerosas incertidumbres asociadas al comportamiento de los distintos tipos de terreno. Tanto la dificultad en la determinación de las características mecánicas d
el terreno real como la complejidad en las hipótesis de cálculo han llevado a la utilización de simplificaciones útiles en una gran mayoría de casos. Las dos teorías clásicas en la estimación de los empujes del terreno se deben al francés Charles-Agustin de Coulomb (1736-1806) y al escocés William John Macquorn Rankine (1820-1872). Ambos métodos se sustentan en hipótesis diferentes y los resultados que proporcionan no coinciden, salvo en algún caso muy particular.
En cualquier libro de Geotecnia se puede comprobar cómo integrando las ecuaciones diferenciales de las condiciones de equilibrio interno de un elemento diferencial de un terreno horizontal, homogéneo, isótropo y con un comportamiento elástico, la tensión horizontal depende de la vertical. En el caso de que el terreno estuviera confinado lateralmente, con deformación lateral nula, la ley de Hooke proporciona una solución al problema, siendo la relación entre la tensión horizontal y la vertical constante. En cualquier caso, la condición de utilizar una ley de esfuerzo-deformación conveniente constituye el mayor obstáculo para obtener una solución exacta al problema.
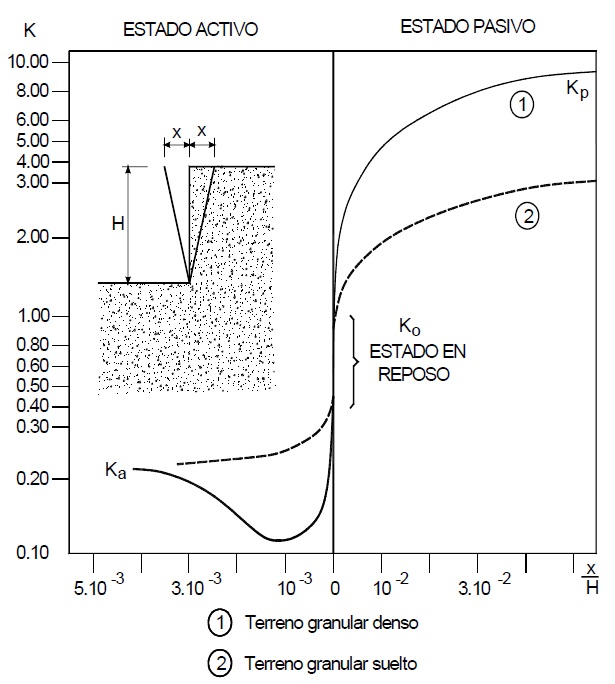
Las presiones que soporta un muro o una pantalla reciben el nombre de empujes, que en el caso más general, será la suma del empuje hidrostático más el empuje efectivo ejercido por las partículas del terreno. Se define el coeficiente de empuje como la relación entre la tensión efectiva horizontal y la vertical, y en el caso de que no exista deformación lateral, se denomina coeficiente de empuje al reposo, K0. De esta forma se podría calcular el empuje sobre un muro que no se deformara lo más mínimo. Sería el caso de un muro de sótano en edificación. Pero los muros no son infinitamente rígidos, se deforman, y dependiendo de si la deformación lateral es negativa (el terreno “se descomprime”) o positiva (el terreno “se comprime”), tendríamos los denominados empujes activos Ka, o pasivos Kp, (Ka<K0<Kp). Para movilizar el empuje pasivo son necesarios movimientos del muro contra el terreno muy superiores a los necesarios para llegar a una situación de empuje activo. Cuando el empuje pasivo es favorable, debido a la imprecisión en la determinación de su valor real, por seguridad suele despreciarse su efecto o bien se aplica un coeficiente reductor (por ejemplo, de 1,5). Dejamos al lector investigar sobre este asunto en la literatura habitual.
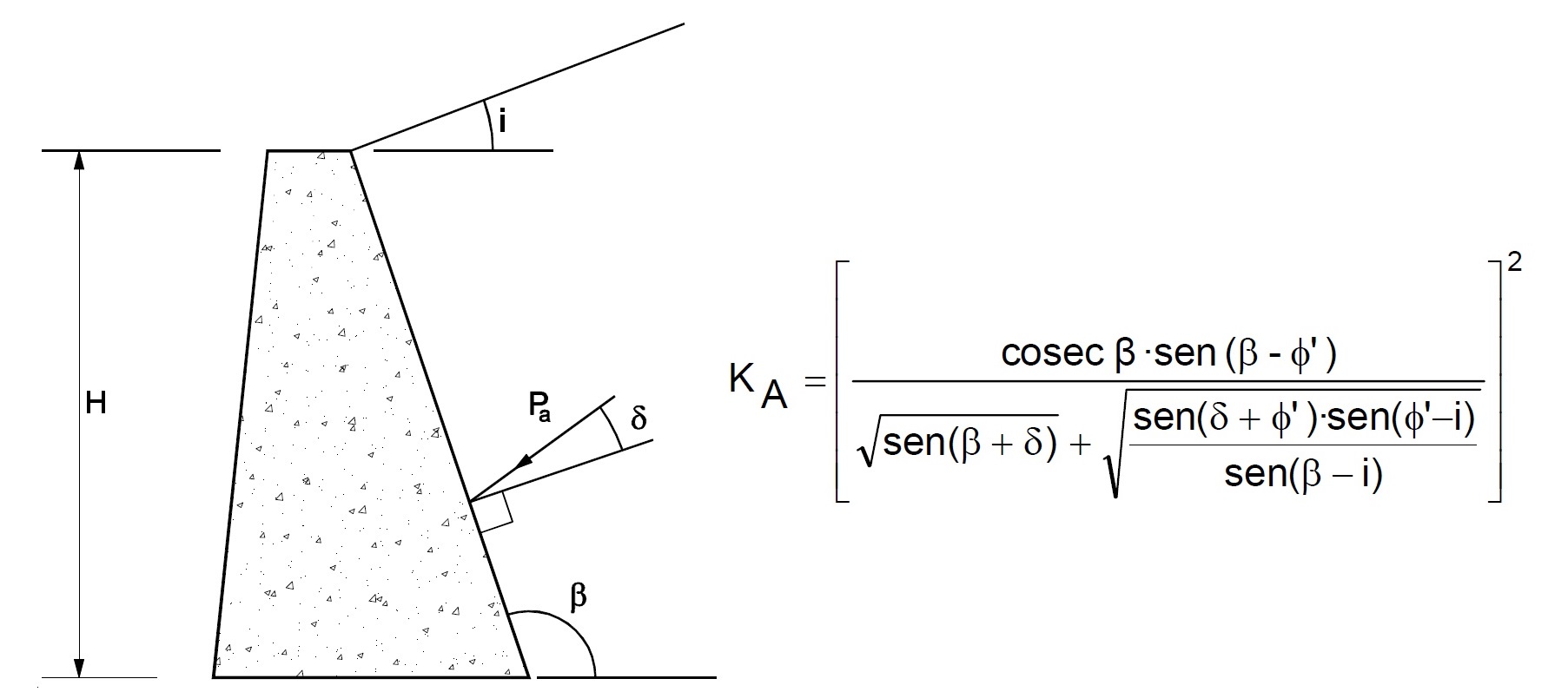
Lo que nos interesa en esta entrada es conocer las diferencias entre el método de Coulomb y el de Rankine e intentar interpretar cuándo sería mejor utilizar uno u otro método. Las fórmulas se pueden deducir de cualquier libro o manual de geotecnia. En ambos casos se puede generalizar la formulación al caso de terrenos cohesivos, presencia de nivel freático, cargas uniformes sobre el trasdós e inclinación del relleno tras el muro. Siendo σ’v es la tensión efectiva vertical y c‘ la cohesión efectiva del terreno o relleno del trasdós, el empuje activo Pa se define como la resultante de los empujes unitarios σ’a que puede determinarse mediante la siguiente fórmula:
y de forma análoga, el empuje pasivo Pp se define como la resultante de los empujes unitarios σ’p que puede determinarse mediante:
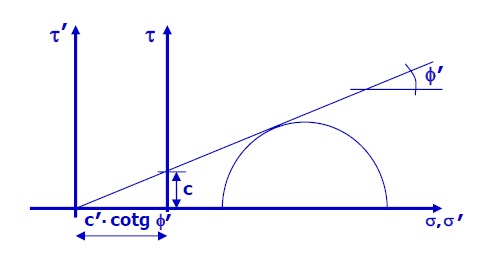
La cohesión es un aspecto favorable para disminuir el empuje del terreno, pero si al final no se acaba desarrollando, nos deja del lado de la inseguridad; por tanto, como a veces es difícil estimar su efecto de forma adecuada, es habitual despreciarla para quedar del lado de la seguridad. Por tanto, se aconseja ser muy cuidadoso a la hora de considerar la cohesión.
- Coulomb propuso un modelo para estimar los empujes del terreno planteando el equilibrio de una masa de terreno en forma de cuña al deformarse o moverse el muro. La rotura se produce a lo largo de dos planos, el formado por el interface suelo-muro y el plano de deslizamiento en el terreno. La cuña, formada por los dos planos, se comporta como un bloque rígido. De todas las cuñas posibles, una es la que produce el empuje activo máximo, y ese es el problema resuelto por este ingeniero francés en 1776. El método supone que las superficies de deslizamiento son planas, pero esta hipótesis es muy discutible en el caso del empuje pasivo. El problema queda resuelto para un muro cualquiera, con un trasdós que no necesita ser vertical, y un terreno con una determinada inclinación y con unas cargas sobre su superficie. Se supone conocido el peso específico del terreno, el ángulo de rozamiento interno y el ángulo de rozamiento muro-suelo. Es actualmente el método más empleado para el diseño de muros por métodos de equilibrio límite. Hoy día se emplea con gran efectividad en el cálculo de muros de gravedad, lo que permite considerables ahorros de material. Las fórmulas que siguen indican los coeficientes de empuje activo y pasivo, con las figuras que definen cada uno de los ángulos correspondientes:
- El método de Rankine (1857) es más elegante desde el punto de vista matemático, explicando el empuje en términos de rotura por cortante del terreno. Se obtienen los empujes partiendo de un semiespacio infinito que se encuentra en “estado de Rankine“, es decir, un estado de equilibrio plástico y en donde el muro no produce ninguna perturbación. Se supone que el terreno es homogéneo e isótropo y en estado de equilibrio plástico, es decir, se acepta que toda la masa en el trasdós del muro está en situación de rotura y, por tanto, en cualquier punto el estado tensional pertenece a un círculo de Morh que es tangente a la línea de rotura de este suelo; además, como hipótesis adicional, no hay variación de tensiones en los puntos de cualquier plano paralelo a la superficie del semiespacio. Este modelo puede resultar un tanto conservador, pues solo considera el ángulo de rozamiento interno del terreno, olvidando el efecto favorable del rozamiento entre el muro y el terreno. Este método tiene muchas aplicaciones prácticas, por ejemplo, en muros ménsula, donde la suposición de Rankine no supone grandes desventajas y simplifica enormemente los cálculos. El cálculo de empujes sobre un muro con el modelo de Rankine se reduce a obtener las presiones efectivas a la profundidad correspondientes y aplicar las fórmulas correspondientes. De esta forma es muy sencillo calcular terrenos estratificados y considerar la existencia de una carga uniforme en coronación. Además, el método permite estimar si existen grietas de tracción y su profundidad en un terreno que sea cohesivo. Los coeficientes de empuje activo y pasivo para un terreno que forma un ángulo i con la horizontal teniendo en cuenta que la resultante forma un ángulo i con la horizontal, son los siguientes:
Aplicando el teorema de los estados correspondientes de Caquot, se puede generalizar la teoría de Rankine a suelos cohesivos: “Si a un suelo con cohesión que está en situación límite de rotura, simultáneamente le quitamos la cohesión y sumamos a todas las tensiones un término (c’ · cotg Φ’), el suelo sigue estando en la misma situación límite de rotura” (y se le aplican las hipótesis de los suelos sin cohesión).
De las fórmulas deducidas para el empuje activo y pasivo, las fórmulas en ambos modelos coinciden únicamente en el caso de un trasdós vertical del muro, no hay rozamiento suelo-estructura y la superficie del terreno es horizontal. En este caso, los coeficientes de empuje activo y pasivo son los siguientes:
Resumiendo los aspectos básicos expuestos anteriormente, podríamos decir lo siguiente:
- En caso de terrenos estratificados, la inclinación del plano de deslizamiento depende de cada terreno, con lo que el problema puede ser indeterminado si utilizamos el modelo de Coulomb. En este caso, Rankine es de más fácil formulación, que suele ser recomendable en el caso de muros ménsula.
- El método de Coulomb no tiene en cuenta la presencia de grietas de tracción, por lo que con terrenos cohesivos el cálculo de la profundidad de estas grietas se debe hacer con Rankine.
- Si no existe cohesión en el terreno ni adherencia entre muro y terreno, con la teoría de Coulomb se puede determinar que la resultante del empuje activo está situada, desde la base del muro, a un tercio de la altura del muro. Si no es así, entonces el método no proporciona directamente la posición del empuje.
- El método de Rankine es difícil de aplicar con geometrías mínimamente complejas (trasdós quebrado, superficies del terreno en el trasdós no planas, cargar arbitrarias sobre éste último) y no es mucho más preciso que el método de Coulomb para estos casos.
- El método de Coulomb no estima bien el empuje pasivo, pues la superficie real de rotura no es plana (se asemeja a una espiral logarítmica) y la distribución de empujes difiere bastante de la triangular, proporcionando valores sobredimensionados (del lado de la inseguridad). El método de Rankine es más conservador para el cálculo de empujes pasivos.
- El método de Rankine no considera el rozamiento entre el muro y el terreno, lo cual es conservador. Es un aspecto importante en muros de gravedad, cuyos empujes activos se prefieren calcular con Coulomb.
- En el método de Coulomb permite la consideración de sobrecargas en el trasdós de cualquier tipo (constante, puntual, triangular, etc.) siempre que sean indefinidas en el sentido longitudinal del muro, pues basta introducirlas en las ecuaciones de equilibrio. Con Rankine es sencillo si se trata de una sobrecarga constante.
REFERENCIAS:
- GARCÍA VALCARCE, A. (dir.) (2003). Manual de edificación: mecánica de los terrenos y cimientos. CIE Inversiones Editoriales Dossat-2000 S.L. Madrid, 716 pp.
- GONZÁLEZ CABALLERO, M. (2001). El terreno. Edicions UPC, Barcelona, 309 pp.
- IZQUIERDO, F.A. (2001). Cuestiones de geotecnia y cimientos. Editorial Universidad Politécnica de Valencia, 227 pp.
- LAMBE, T.W.; WHITMAN, R.V. (1996). Mecánica de suelos. Limusa, México, D.F., 582 pp.
- MINISTERIO DE FOMENTO (2002). Guía de Cimentaciones. Dirección General de Carreteras.
- MINISTERIO DE LA VIVIENDA (2006). Código Técnico de la Edificación
- YEPES, V. (2020). Procedimientos de construcción de cimentaciones y estructuras de contención. Colección Manual de Referencia, 2ª edición. Editorial Universitat Politècnica de València, 480 pp. Ref. 328. ISBN: 978-84-9048-903-1.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.