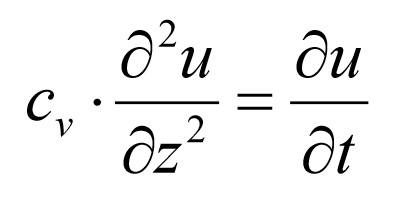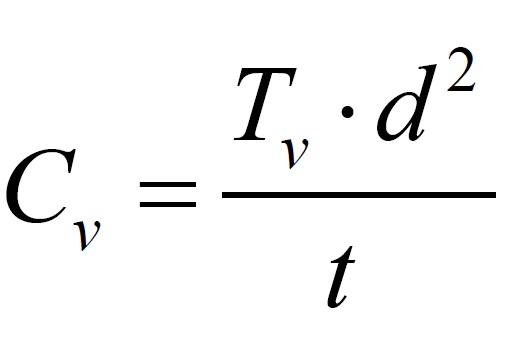Una de las paradojas que planteó el filósofo Zenón de Elea es que si para ir a un lugar recorres primero la mitad de la distancia, luego la mitad de la distancia que te queda por recorrer, y así hasta el infinito, nunca llegarás a tu destino, aunque estés toda la vida andando. Esta paradoja se solucionó matemáticamente en el siglo XIX al aceptar que la suma de 1/2 + 1/4 + … suman 1. Pues bien, un terreno saturado al que sometemos a una carga va a asentar de forma indefinida, pero no superará un valor tope determinado. Veamos esto con mayor detalle.
En un artículo anterior vimos hablamos del Principio de Terzaghi, por el cual un terreno se deforma solo cuando existe un cambio en sus tensiones efectivas. Cuando se carga un terreno saturado, éste tiene la costumbre provocar asientos que se incrementan con el tiempo, siempre que sea posible el drenaje. Esto plantea la pregunta de si los asientos crecerán de forma indefinida con el tiempo. Afortunadamente, el asiento tiende asintóticamente a una magnitud última a la cual se llegará, eso sí, en tiempo infinito.
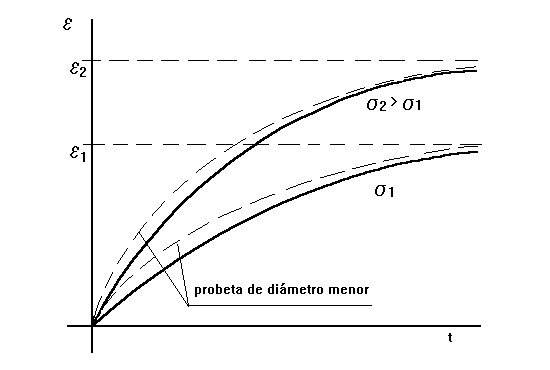
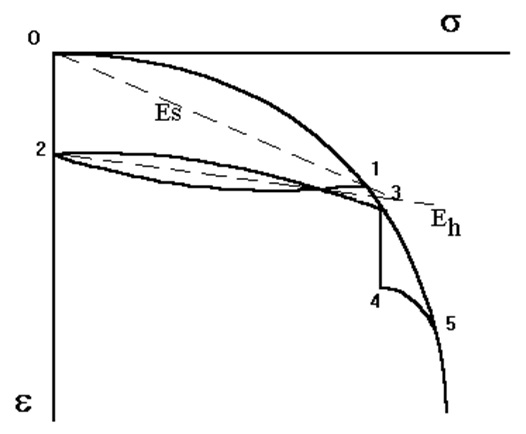
Pero empecemos por el principio. En presencia de un sólido homogéneo, isótropo y linealmente elástico, la teoría de la elasticidad nos permite conocer perfectamente la deformación que tendrá ante un incremento de cargas. Para ello basta conocer el módulo de elasticidad E y el coeficiente de Poisson ν. Es más, si estamos ante este tipo de terreno y conocemos las ecuaciones de Hooke en términos efectivos (es decir, conocemos E‘ y γ’, obtenidos en suelo drenado, a largo plazo), entonces tenemos herramientas para averiguar la deformación del terreno, tal y como vimos en el artículo que donde hablábamos de los asientos de cargas rectangulares en el semiespacio de Boussinesq. Este método sería válido para cargas de servicio o de trabajo, alejadas de la carga de rotura (factor de seguridad del orden de 3), que probablemente generen asientos elásticos. El método elástico será tanto más aceptable cuanto más se asemeje el comportamiento del suelo al del sólido lineal-elástico, como es el caso de los suelos granulares o las arcillas fuertemente sobreconsolidadas, bajo presiones normales de cimentación.
Sin embargo, no vamos a tener tanta suerte. El comportamiento del suelo es más complejo. De hecho, la deformación ocurrirá, tal y como se ha comentado anteriormente, cuando las presiones efectivas empiecen a cambiar. Y eso tendrá lugar si se permiten disipar las presiones intersticiales del terreno. Por tanto, las deformaciones van a depender, entre otros factores, de la permeabilidad. Terrenos altamente permeables, como gravas o arenas, van a deformar rápidamente, puesto que el agua drenará con mucha facilidad. Pero terrenos más impermeables como las arcillas, el proceso se dilatará en el tiempo. Es el fenómeno conocido como consolidación.
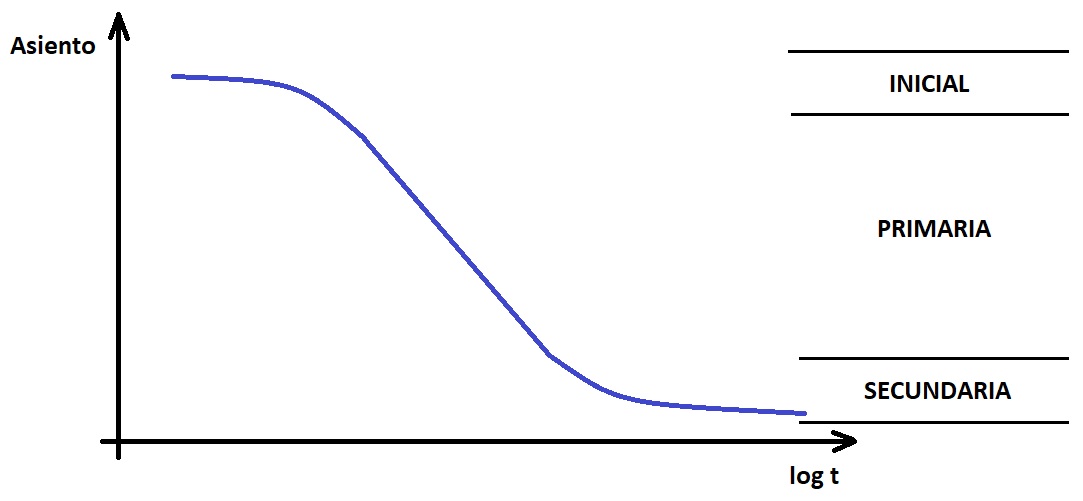
Por tanto, ante un terreno saturado, tenemos tres tipos de consolidación. La consolidación inicial la provoca un aumento de la presión total, que provoca un cambio de volumen debido a efectos como la disolución de las burbujas de aire, el cierre de fisuras o la reordenación de las partículas, entre otras posibles causas. La consolidación primaria, es provocada por el aumento de la presión efectiva como consecuencia de la disipación de las sobrepresiones intersticiales. Por último, la consolidación secundaria se produce a tensión efectiva constante, es decir, una vez disipada la sobrepresión intersticial y se debe a factores como la fluencia por desplazamientos y reorientaciones de partículas, o bien a la descomposición de la materia orgánica del suelo, entre otras posibles causas.
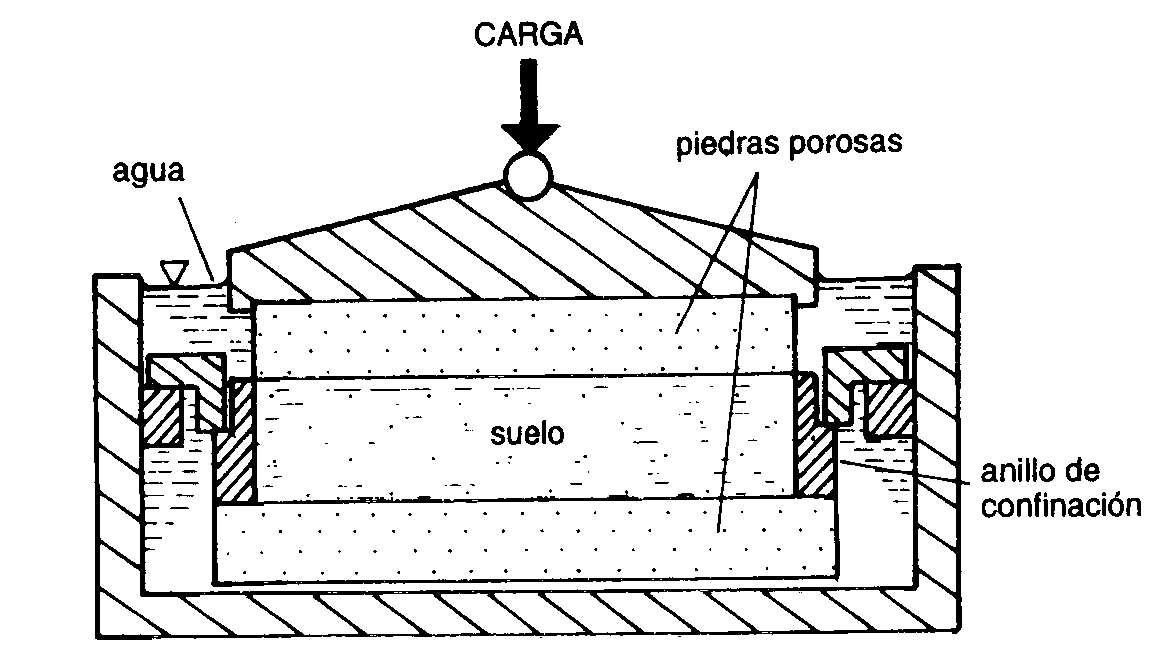
Para determinar tanto la magnitud de la deformación de un suelo al aumentar la tensión efectiva a la que está sometido (curva edométrica), como la velocidad a la que ocurre el asiento de consolidación (curva de consolidación), se utiliza el ensayo edométrico. De este ensayo y sus características hablaremos en otros artículos.
Pero aquí lo que queremos es ver cómo evolucionan los asiento con el tiempo durante el proceso de consolidación. En un proceso unidimensional, la ecuación que gobierna dicho proceso es la siguiente:
donde Cv es el denominado coeficiente de consolidación vertical, que depende del nivel de tensiones existente y cuyas unidades son [L2]/[T]. Este coeficiente en una arcilla puede deducirse de un ensayo edométrico de una muestra inalterada. Su valor tipo oscila entre 0,4 x 10-4 y 3 x 10-3 cm2/s, y los valores deducidos in situ oscilan entre 0,7 x 10-4 y 250 cm2/s (González Caballero, 2001).
Si definimos como grado de consolidación U la relación entre el asiento experimentado en un instante por el suelo respecto al asiento total, podemos utilizar U como variable auxiliar adimensional para resolver la ecuación diferencial anterior.
Si llamamos factor de tiempo a Tv, éste se encuentra relacionado con U. La solución simplificada de la ecuación diferencial, suponiendo que el incremento de presión total es uniforme o lineal en el caso del doble drenaje, nos lleva a dos ecuaciones sencillas, que son las siguientes: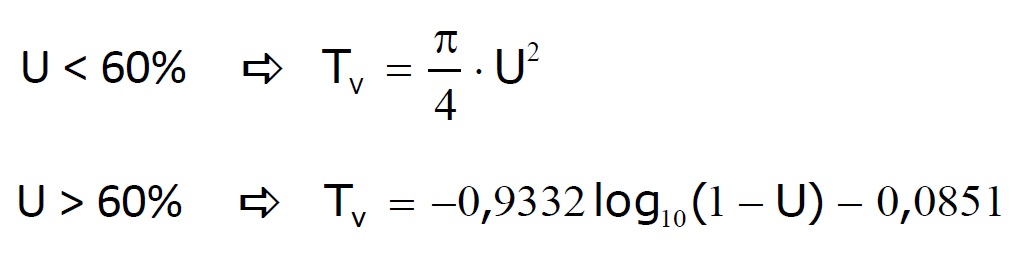
Estas expresiones las hemos dibujado en la Figura 3, donde se relaciona U con Tv. Se puede observar que para el grado de consolidación del 100%, el factor de tiempo se hace infinito. No obstante, se puede considerar que un factor de tiempo Tv = 2 corresponde prácticamente al final de la consolidación primaria.

Además, el coeficiente de consolidación vertical Cv está relacionado con el factor de tiempo Tv, con la distancia libre de drenaje d y con el tiempo t a través de la siguiente expresión:
Por tanto, se puede saber el tiempo que tardará en asentar un suelo saturado para alcanzar un grado de consolidación determinado conociendo la distancia libre de drenaje y el coeficiente de consolidación vertical. Los cálculos pueden realizarse rápidamente utilizando la gráfica de la Figura 4. Se ha dibujado el eje vertical en escala logarítmica. Cada función indica una longitud libre de drenaje distinta.
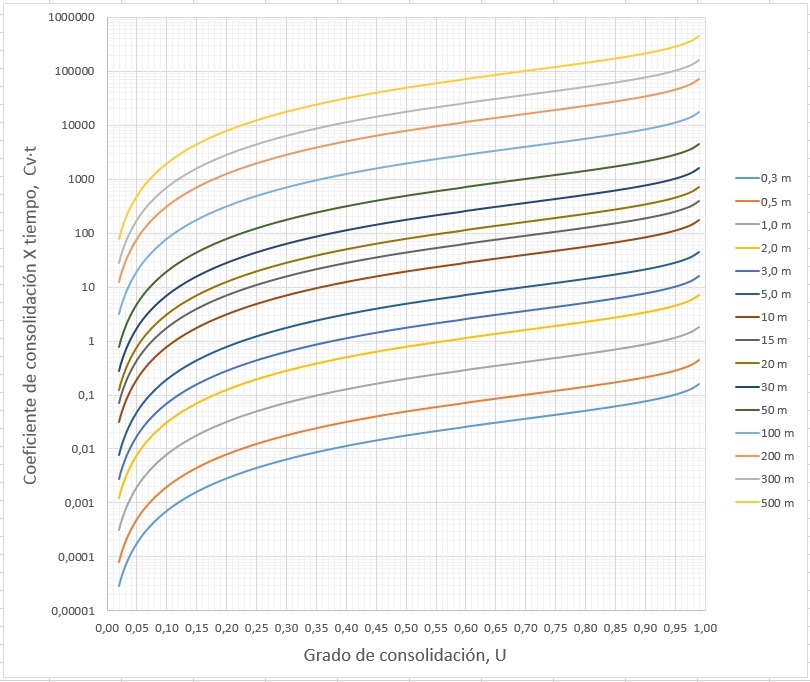
Vamos a hacer un cálculo aproximado utilizando la Figura 4. Si suponemos una arcilla con un coeficiente de consolidación Cv = 1,0 m2/año, en el periodo de 1 año, con una longitud de drenaje de 1 m, se habrá superado más del 90% del asiento previsto, pero si la longitud de drenaje es de 2 m, no llegaremos al 60% del asiento.
Se deja al lector curioso la demostración de que si la longitud de drenaje la dividimos por n, entonces el tiempo que se tardará en alcanzar el mismo grado de consolidación se divide por n2 . Así, por ejemplo, una capa de arcillas dispuesta entre dos capas de material granular tardará en alcanzar un mismo asiento en la cuarta parte del tiempo que si dicha capa estuviese dispuesta entre una capa granular y otra impermeable.
Referencias:
- DAS, B. (2005). Fundamental of Geotechnical Engineering – 2nd ed, Technomic Publishing Co.
- GONZÁLEZ CABALLERO, M. (2001). El terreno. Edicions UPC, 309 pp.
- GONZÁLEZ DE VALLEJO, L.I. et al. (2004). Ingeniería Geológica. Pearson, Prentice Hall, Madrid.
- IZQUIERDO, F.A. (2001). Cuestiones de geotecnia y cimientos. Editorial Universidad Politécnica de Valencia, 227 pp.
- YEPES, V. (2020). Procedimientos de construcción de cimentaciones y estructuras de contención. Colección Manual de Referencia, 2ª edición. Editorial Universitat Politècnica de València, 480 pp. Ref. 328. ISBN: 978-84-9048-903-1.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.