Categoría: calidad

El mito de la ISO 9001: por qué tu «calidad» está matando tu agilidad operativa.

Durante años, la norma ISO 9001 ha sido víctima de una mala interpretación sistémica. En muchas salas de juntas, la palabra «calidad» no evoca excelencia, sino una imagen lúgubre de estanterías llenas de manuales que nadie lee y de una burocracia asfixiante que ralentiza cada decisión. A esto es a lo que yo llamo «la muerte por papel»: un estado en el que la organización trabaja para el sistema en lugar de ser el sistema quien trabaje para la organización.

Sin embargo, si eliminamos el cumplimiento superficial, lo que queda no es un obstáculo reglamentario, sino un sistema de inteligencia estratégica de alto nivel. La ISO 9001, entendida desde la perspectiva de la madurez organizacional, es, en realidad, el «sistema operativo» de los negocios modernos. Si tu certificación se siente como un lastre y no como una palanca para aumentar el retorno de la inversión (ROI), es probable que estés cometiendo los errores que separan a las empresas que solo «tienen el sello» de las que dominan su mercado.

A continuación, expongo cinco verdades disruptivas extraídas de la esencia técnica de la norma que obligarán a cualquier líder a replantearse su modelo de gestión.

1. El gran pecado de la burocracia autoimpuesta.

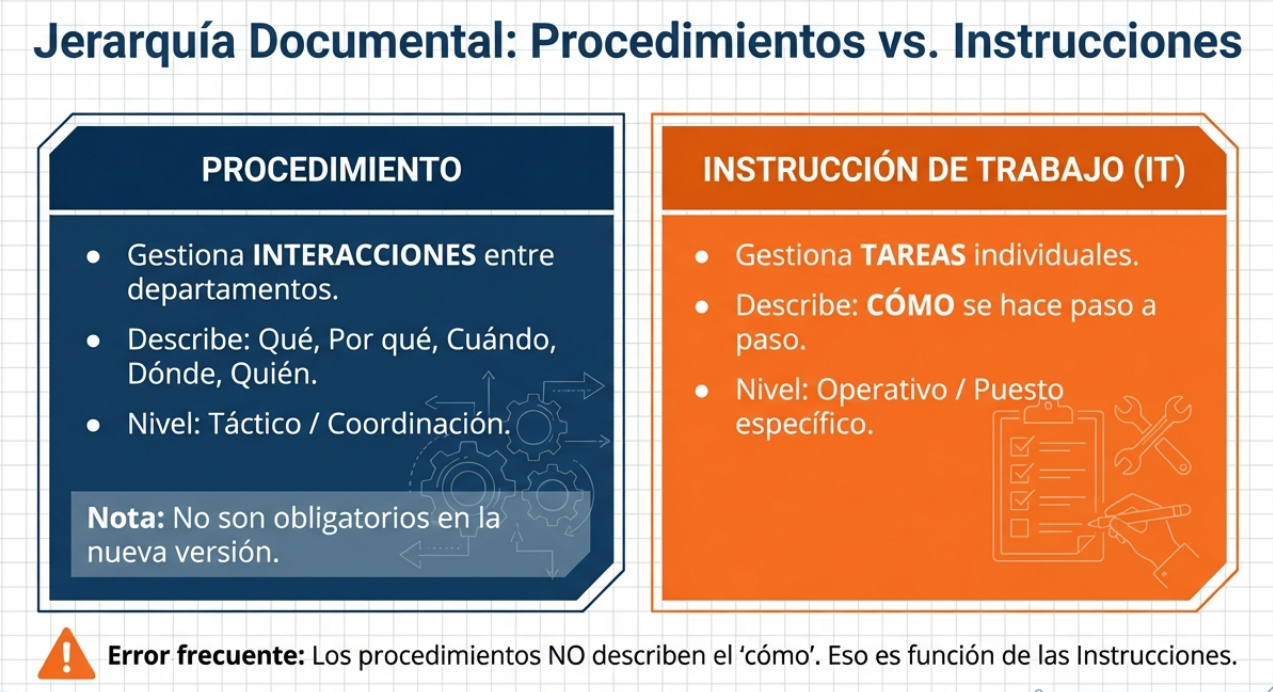
La principal fuente de fricción operativa es la confusión entre procedimientos e instrucciones de trabajo. Muchas empresas documentan cada paso de cada tarea en «procedimientos» densos, creando una red de la que es imposible escapar. El consultor sénior sabe que el procedimiento describe el qué, el porqué y quién es el responsable, mientras que el cómo detallado pertenece exclusivamente a las instrucciones de trabajo.

Sin embargo, la verdad más sorprendente, que la mayoría de los gestores ignora, es la siguiente:

Los procedimientos del sistema de gestión de la calidad, según la norma ISO 9001, describen la implementación de dicho sistema. No son obligatorios.

Así es. La norma no te obliga a tener esa montaña de procedimientos. Si tu sistema es burocrático, es por decisión interna, no por exigencia del estándar. La agilidad se recupera cuando se entiende que la ISO busca resultados, no literatura.

2. La estructura de alto nivel.

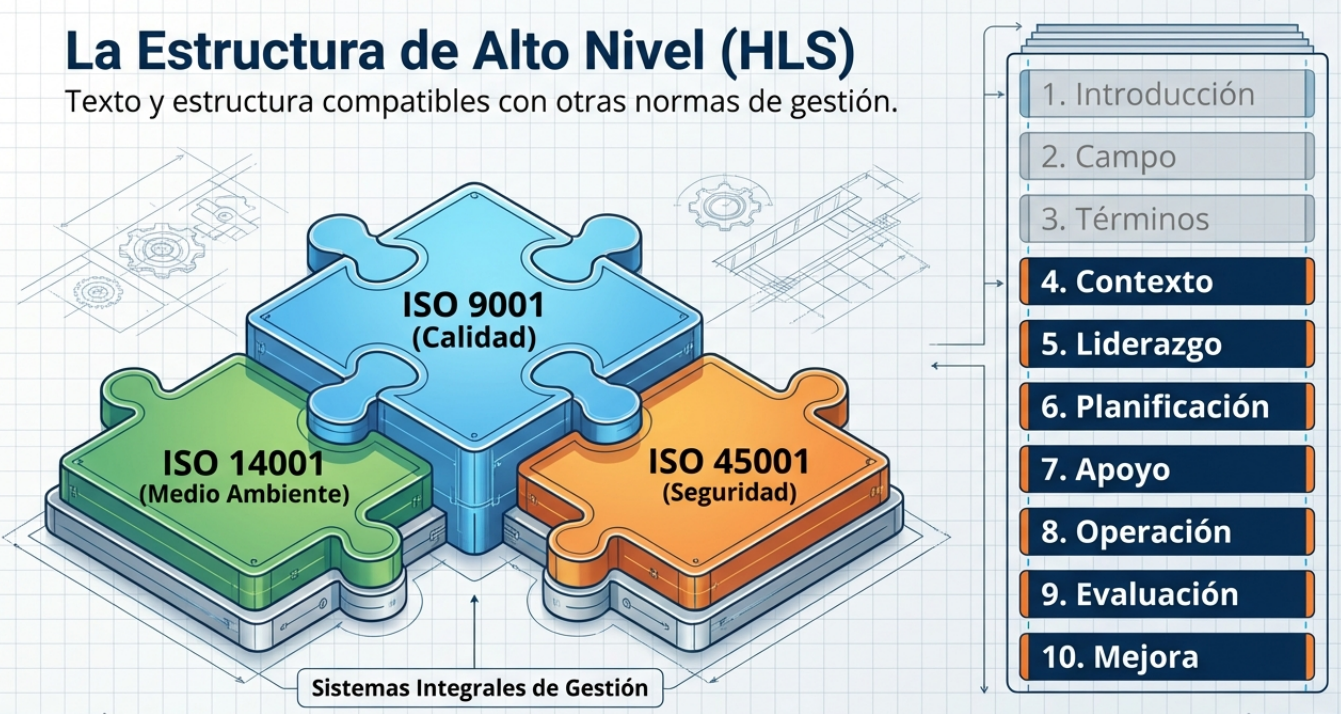
La ISO 9001 ya no es una isla. Gracias a su Estructura de Alto Nivel, ahora utiliza un lenguaje universal compatible con otros estándares. Esto no es solo un detalle técnico, sino la base para crear sistemas integrales de gestión.

En lugar de tener departamentos estancos que gestionan por separado los riesgos ambientales, de seguridad o de calidad, esta estructura permite integrarlos.

  • ISO 14001: Gestión Ambiental.
  • ISO 45001: Seguridad y salud en el trabajo.

Esta compatibilidad transforma el sistema de gestión en un tronco común que optimiza los recursos de auditoría y, lo que es más importante, elimina la redundancia de datos, de modo que la dirección tenga una visión única de la resiliencia corporativa.

3. El riesgo invisible: de la expectativa voluntaria al requisito legal.

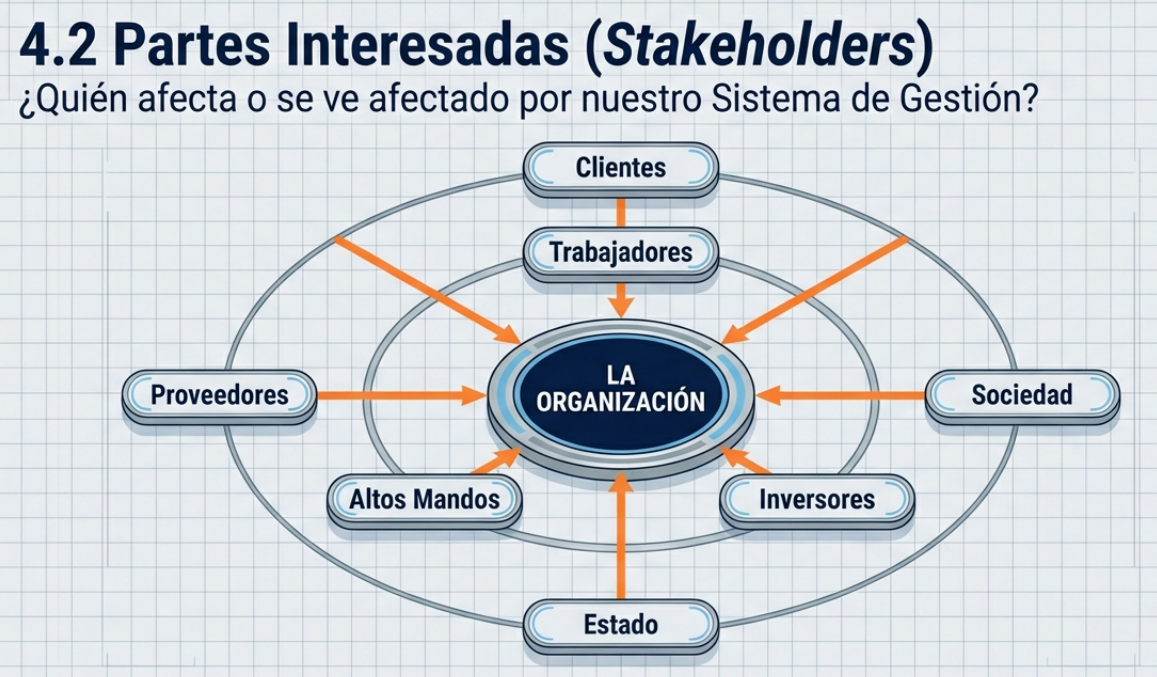
Muchos gestores limitan su visión al cliente final. La norma, sin embargo, exige un enfoque de 360 grados respecto de las partes interesadas. Pero cuidado: el análisis de sus necesidades no es un ejercicio de relaciones públicas, sino una trampa de cumplimiento si no se gestiona con inteligencia estratégica.

Tomemos como ejemplo una empresa de transporte de mercancías. Para un inversor, la «calidad» no solo consiste en que el camión llegue a tiempo, sino que también abarca la imagen de la reputación y el control de riesgos económicos. Para un trabajador, son el reconocimiento y la participación. Lo verdaderamente crítico es que la organización puede decidir aceptar voluntariamente estas expectativas (por ejemplo, mediante un contrato o una promesa de marca).

Muchos se sorprenden al descubrir que una vez que la organización adopta voluntariamente un requisito de una parte interesada, este se convierte automáticamente en un requisito obligatorio del sistema de gestión. Un compromiso contractual con un proveedor sobre plazos de pago o una promesa de sostenibilidad para la sociedad se vuelve tan auditable y legalmente vinculante para tu sistema de calidad como la entrega del producto mismo.

4. Verificación frente a validación: la diferencia entre cumplir y satisfacer.

En la alta dirección, confundir estos términos es una receta para el desastre financiero. La diferencia es sutil, pero vital para garantizar el valor real:

  • Verificación: Confirmación, mediante inspección, de que se han cumplido los requisitos especificados. Se trata de una comprobación frente al plano o al diseño.
  • Validación: Comprobación, mediante ensayo, de que el producto cumple su aplicación específica prevista en el mundo real.

Un producto puede estar perfectamente verificado (cumplir todas las especificaciones técnicas) y ser un fracaso total si no ha sido validado (no sirve para lo que el usuario necesitaba). Un gestor estratégico no se detiene en la inspección, sino que busca el ensayo que demuestre su utilidad real.

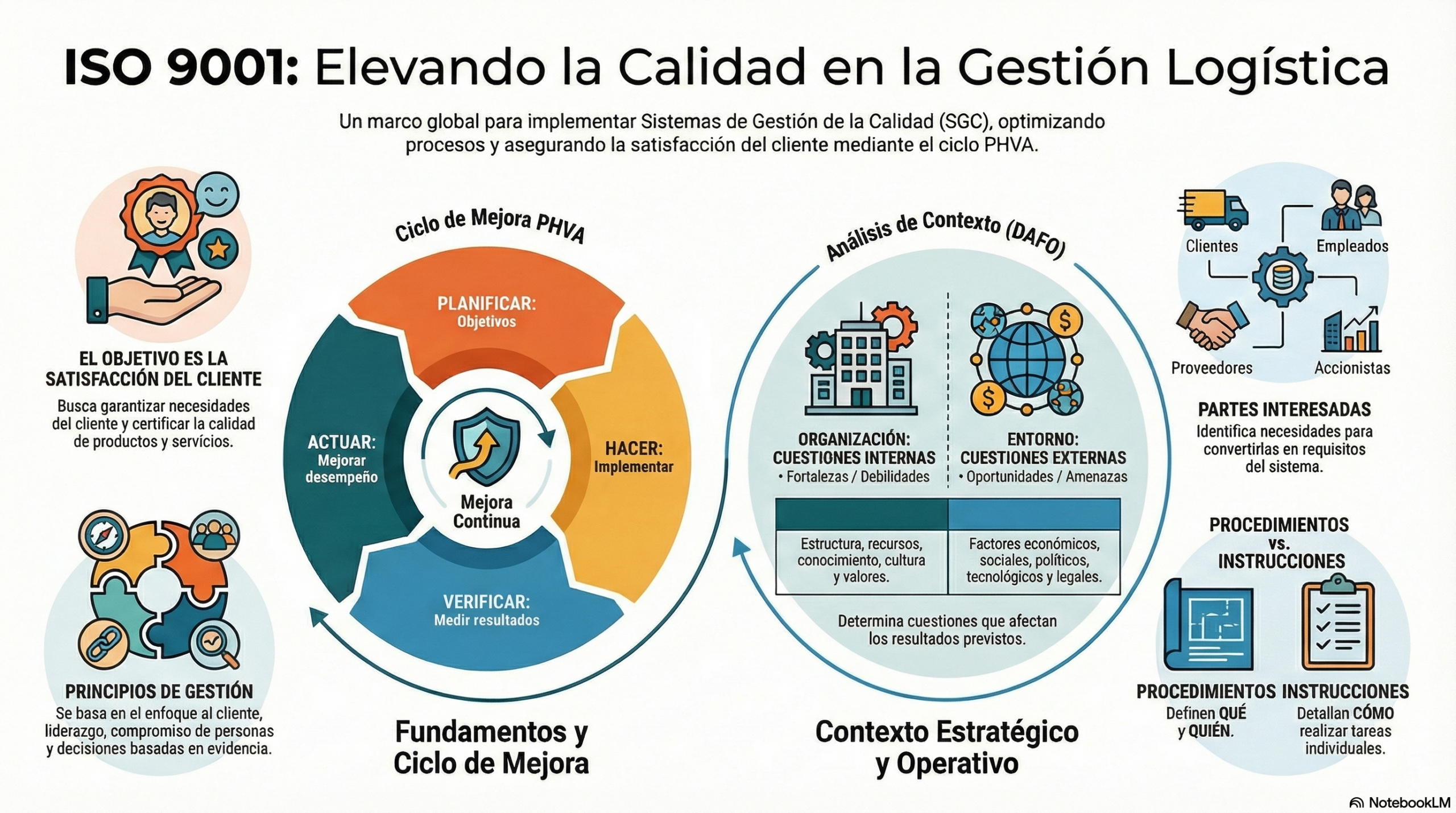
5. El liderazgo como eje del PDCA.

El ciclo PDCA (Planificar, Hacer, Verificar, Actuar) suele representarse como un círculo estático. Es un error. En el modelo real de la ISO 9001, el liderazgo no es un paso más del ciclo, sino el eje central que mantiene todos los procesos en órbita y en armonía. Sin liderazgo, el ciclo se fragmenta.

Para que este motor genere mejora continua y no solo «mantenimiento», debe nutrirse de la toma de decisiones basada en la evidencia. La norma es el antídoto contra la gestión por intuición. En la fase de «Actuar», el sistema no solo busca corregir el fallo, sino también eliminar su causa raíz para que no vuelva a ocurrir. Esto solo es posible si los líderes utilizan los datos del sistema para abordar riesgos y oportunidades, en lugar de reaccionar visceralmente ante las crisis diarias.

Conclusión: ¿activo estratégico o certificado decorativo?

La calidad no es un destino, sino una cultura de mejora continua que debe reflejar la salud de tu dirección estratégica. Si analizamos el contexto de una empresa de transporte mediante un análisis DAFO, veremos que factores externos como la fluctuación del precio del combustible o las nuevas regulaciones medioambientales no son «problemas de logística», sino variables de calidad.

En última instancia, tu sistema de gestión de la calidad debería poder responder a las preguntas más difíciles de tu análisis estratégico: ¿por qué un cliente potencial compra a tu competencia y no a ti? ¿Qué le falta a tu servicio para ser verdaderamente superior?

Si tu sistema no te ayuda a responder estas preguntas, no tienes un sistema de gestión, sino un certificado en la pared. La verdadera ISO 9001 es una plataforma para potenciar tus fortalezas y mitigar amenazas antes de que se conviertan en crisis. La pregunta es: ¿estás listo para dejar de «cumplir» y empezar a competir?

En esta conversación puedes escuchar algunas de las ideas más interesantes del tema.

En el vídeo se sintetizan algunos de los aspectos más relevantes de la norma ISO 9001.

ISO_9001_Logistics_and_Transport

Licencia de Creative Commons
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Gestión y normativa de sostenibilidad medioambiental

En el entorno corporativo actual, la presión por ser «sostenible» es omnipresente. Sin embargo, existe una brecha crítica entre el marketing ecológico y la capacidad real de ejecución. Para un líder estratégico, la sostenibilidad no es una mera declaración de intenciones, sino una cuestión de arquitectura organizativa.

Un Sistema de Gestión Ambiental (SGA) es, en esencia, la forma en que las empresas se organizan, mediante estructuras y procesos definidos, para actuar de manera sistemática, garantizar la fluidez de las operaciones y alcanzar los resultados previstos.

A continuación, se desglosan cinco ideas que te permitirán pasar de la intuición a la estructura y optimizar la competitividad de tu organización conforme a estándares internacionales.

Flexibilidad estratégica: el mito de las metas cuantitativas en la ISO 14001.

Existe la creencia errónea de que la certificación ISO 14001 impone límites uniformes de emisiones a todas las empresas. En realidad, esta norma no dicta resultados, sino que facilita procesos. Como estratega, debes entender que la serie ISO 14000 proporciona un marco lógico que se adapta a tu realidad operativa, ya sea que dirijas una multinacional como Toyota o una empresa de servicios.

Como aclara el estándar técnico:

«No establece un conjunto de objetivos cuantitativos en cuanto a niveles de emisiones ni métodos específicos para medirlos».

Esta característica es la que otorga flexibilidad estratégica. La norma te obliga a identificar tus propios riesgos y externalidades, lo que te permite fijar objetivos acordes con tu modelo de negocio y tus recursos disponibles, garantizando siempre una mejora en el desempeño ambiental.

Resiliencia operativa: el ciclo PHVA como motor de eficiencia.

Un sistema de gestión ambiental (SGA) eficaz no es una foto estática, sino un sistema dinámico diseñado para combatir el estancamiento corporativo. El motor de esta resiliencia es el ciclo PHVA (Planificar-Hacer-Verificar-Actuar), que convierte la gestión ambiental en un flujo operativo constante.

  • Planificar: Definición de objetivos y procesos alineados con la política ambiental de la empresa.
  • Hacer: Ejecución e implementación de los procesos según lo previsto.
  • Verificar: Fase crítica de seguimiento y medición de los compromisos, en la que se evalúan no solo los objetivos, sino también los criterios de operación establecidos.
  • Actuar: Tomar decisiones basadas en datos para optimizar el sistema de forma continua.

Este ciclo garantiza que la gestión ambiental sea un proceso de optimización continua y no un evento aislado para cumplir con una auditoría.

Integración de sistemas: el valor estratégico de la Estructura de Alto Nivel (HLS)

Para los directivos que temen la parálisis burocrática, la Estructura de Alto Nivel (HLS) es la solución definitiva. Las versiones modernas de las normas ISO comparten un texto básico y definiciones comunes. Esto no solo simplifica los trámites administrativos, sino que también ofrece la oportunidad de lograr una integración estratégica.

La implementación de la HLS permite que normas como la ISO 14001 (medio ambiente), la ISO 9001 (calidad) y la ISO 45001 (seguridad y salud) hablen el mismo idioma. Al tratarse de requisitos comunes, el esfuerzo documental se reduce drásticamente, ya que lo único que varía es el enfoque aplicado. Puede gestionar sus responsabilidades legales y operativas desde una única plataforma documental, lo que elimina los silos organizativos y el caos de múltiples sistemas aislados.

 

El rigor en la medición: la ISO 14064 frente a la ISO 14067

Anunciar una «huella de carbono» sin definir sus límites supone un riesgo para la reputación. Según la norma ISO 14064, la credibilidad de sus cifras depende de dos decisiones técnicas cruciales que todo director ejecutivo debe validar:

  • Límites organizativos: ¿Informará desde un enfoque de control (emisiones sobre las que tiene potestad operativa o financiera) o desde un enfoque de cuota de participación (emisiones proporcionales a su capital accionario)?
  • Límites operativos: identificación precisa de los tipos de emisiones (directas e indirectas) que se integran en el inventario anual.

Además, como consultor sénior, es fundamental que su equipo no confunda los términos: la ISO 14064 se centra en la huella de la organización, mientras que si su objetivo es certificar el impacto de un producto o servicio específico, debe recurrir a la ISO 14067. Sin esta distinción, su informe de sostenibilidad carecerá de la transparencia y la veracidad necesarias ante los grupos de interés externos.

El desafío del rediseño: por qué la sostenibilidad no se «compra»

Implementar un SGA no es una transacción, sino una transformación. Un sistema mal gestionado puede convertirse en una «fábrica de papel» si no se aborda con una mentalidad eficiente. El «lado B» de la gestión ambiental exige reconocer tres factores ineludibles:

  • Reestructuración de procesos: la implantación suele requerir cambios profundos en la forma en que opera la empresa, lo que demanda inversión técnica y financiera.
  • Compromiso de la alta dirección: sin la implicación directa de los líderes, el sistema se convierte en un ejercicio burocrático estéril.
  • Gestión documental estratégica: un SGA genera abundantes registros, instrucciones técnicas y procedimientos. La clave para evitar el colapso administrativo es automatizar los procesos rutinarios e integrar estratégicamente la documentación.

Conclusión: la gestión ambiental es gestión de la eficiencia

Los casos de éxito de empresas líderes como Toyota, 3M y Ford demuestran que un sistema de gestión ambiental (SGA) robusto es sinónimo de competitividad. Toyota ha reducido drásticamente su consumo de agua y energía, 3M ha logrado minimizar la contaminación y el desperdicio de recursos y Ford ha transformado sus plantas mediante la eficiencia energética y prácticas de reciclaje de vanguardia.

Un sistema de gestión ambiental aporta el orden y la coherencia necesarios para transformar preocupaciones dispersas en una estructura sistemática de responsabilidades.

La pregunta ya no es si su empresa tiene la intención de ser sostenible, sino si su estructura organizativa actual es lo suficientemente sólida como para sobrevivir y prosperar sin un sistema de gestión formal.

En esta conversación puedes escuchar las ideas más interesantes sobre los sistemas de gestión ambiental.

Este vídeo resume bien los conceptos más importantes del tema.

Aquí dejo un documento que sirve como resumen.

Environmental_Management_and_ISO_Standards

Licencia de Creative Commons
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

¿Por qué lo «perfecto» no existe? Claves sobre la capacidad de tus procesos

1. Introducción: El espejismo del resultado idéntico.

Para cualquier líder de operaciones, existe una frustración que roza lo existencial: el espejismo de un resultado idéntico. A pesar de contar con manuales de procedimientos exhaustivos y formación constante, la realidad se impone con una tozudez estadística.

Como veremos, la variabilidad es la fuerza invisible que define el éxito o el fracaso de una organización. Comprender que la perfección no es una meta, sino una asíntota, es el primer paso para pasar de una gestión basada en la intuición a otra basada en la excelencia estratégica.

2. La inevitabilidad de la diferencia: «Nunca dos salidas de un proceso son iguales».

La variabilidad no es un error del sistema, sino su huella dactilar. Un proceso es un conjunto de actividades interrelacionadas en las que interactúan los métodos, la mano de obra, las máquinas, la materia prima y el entorno. En esta danza de variables, la uniformidad absoluta es físicamente imposible.

Desde la perspectiva de W. Edwards Deming, la calidad no es una aspiración abstracta, sino «un grado predecible de uniformidad y fiabilidad, a bajo coste y adecuado a las necesidades del mercado». Desde esta óptica, el objetivo no es eliminar la variabilidad de forma ingenua, sino reducirla para aumentar la predictibilidad.

Es crucial distinguir aquí los llamados «procesos especiales», es decir, aquellos en los que no es posible verificar fácilmente y a un precio asequible la conformidad del resultado. En estos casos, la excelencia no se mide en el producto final, sino en un control férreo y anticipado de las entradas (especialmente de los métodos y la mano de obra), ya que cualquier desviación conlleva un riesgo financiero latente.

«Nunca dos resultados son exactamente iguales».

3. La regla del 90/10: ¿de quién es realmente la culpa?

Uno de los errores más costosos y moralmente desgastantes en la gestión es malinterpretar el origen de las desviaciones. Para liderar con integridad, es imperativo distinguir entre:

  • Causas comunes (o aleatorias): representan más del 90 % de los problemas de calidad. Se manifiestan de forma estable y son inherentes al diseño del sistema. Su corrección es responsabilidad exclusiva de la dirección, ya que requiere cambios estructurales. Intentar corregirlas mediante acciones locales es, matemáticamente, un ejercicio de futilidad.
  • Causas especiales (o asignables): representan menos del 10 % de los fallos. Tienen una distribución errática y esporádica. Estas causas sí corresponden al operario, quien debe actuar para devolver el proceso a su estado normal.

Culpar a un trabajador por un fallo derivado de una causa común es una injusticia estadística. Si el diseño del proceso es deficiente, ningún esfuerzo individual podrá rescatarlo.

4. Control frente a la capacidad: no basta con ser estable.

Un proceso puede ser perfectamente predecible y, al mismo tiempo, completamente inútil para el mercado. La estabilidad es una métrica interna, mientras que la capacidad es una métrica externa de supervivencia.

  • La realidad del proceso (6 sigma): representa lo que el sistema «sabe hacer». Se trata de su variabilidad natural bajo control estadístico, operando dentro de un modelo probabilístico predecible.
  • Las especificaciones son los límites (USL y LSL) que el mercado o la norma establece de forma voluntaria. Representa lo que el cliente está dispuesto a pagar.

La estabilidad es solo la mitad del camino. Un proceso estable, pero descentrado, o con una dispersión mayor que la especificada, es, en términos empresariales, una fábrica de desperdicios.

5. El arte de centrar: la solución más económica.

Ante un proceso «incapaz», la reacción visceral de muchos comités de dirección es aprobar inversiones masivas en nueva maquinaria. Sin embargo, el análisis de capacidad nos ofrece una alternativa estratégica: el centrado.

A menudo, un proceso no es eficaz porque sea errático, sino porque su valor medio no se alinea con el valor nominal del cliente. Identificar un proceso con baja variabilidad, pero descentrado, es como encontrar una mina de oro, ya que permite cumplir los requisitos con ajustes técnicos mínimos en lugar de recurrir a costosas adquisiciones de capital. La diferencia radica en gestionar con base en suposiciones o en datos.

6. Los números hablan: el veredicto del Cp y el Cpk.

Los índices de capacidad no son simples números, sino el veredicto financiero sobre la viabilidad de su operación. Convierten la estadística en decisiones de inversión:

  • Cp (capacidad potencial): revela lo que el proceso podría ser si estuviera perfectamente centrado. Mide si el «ancho» de su proceso se ajusta al del cliente.
  • Cpk (capacidad real): es el indicador honesto y pesimista. Tiene en cuenta el centrado actual y nos indica qué ocurre en este momento.

El análisis de estos índices dicta el camino a seguir.

  1. Si el índice es < 1, el proceso es incapaz. Es un drenaje financiero; genera defectos sistemáticos y requiere un cambio estructural inmediato o la compra de nuevos equipos.
  2. Si el índice es = 1, el proceso es justamente capaz. Es un equilibrio precario en el que cualquier mínima perturbación generará pérdidas.
  3. Si el índice es > 1, el proceso es capaz. Existe un margen de seguridad que garantiza la fiabilidad y el cumplimiento a bajo coste.

7. Conclusión: hacia una cultura de la variabilidad controlada.

La mejora de la calidad consiste, en esencia, en reducir de manera metódica la variabilidad. La estadística nos otorga el poder de la profecía, ya que nos permite garantizar el cumplimiento de las promesas hechas al cliente antes incluso de que la primera unidad salga de la línea de producción.

Como líderes, debemos aceptar que la variabilidad es inevitable, pero su descontrol es opcional. La próxima vez que su operación falle, antes de buscar un culpable en la planta, analice las cifras.

¿Está fallando su proceso por un error puntual o está simplemente diseñado para no poder ganar nunca?

En esta conversación puedes escuchar los conceptos más interesantes sobre este tema.

Este vídeo resume bien los aspectos relacionados con la capacidad de los procesos.

Licencia de Creative Commons
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Cómo se construye la confianza: claves del control de calidad en las estructuras de edificación

Introducción: El sistema nervioso invisible de un edificio.

Cualquiera que haya pasado junto a una obra habrá visto la escena: grúas que se elevan hacia el cielo, un esqueleto de armaduras de acero esperando el hormigón y un ir y venir constante de los trabajadores. Vemos el progreso físico, la estructura que crece día a día. Pero ¿te has parado a pensar en los procesos invisibles que garantizan que ese gigante de hormigón y acero no solo se mantenga en pie, sino que también sea seguro durante décadas?

Detrás de cada pilar, viga y forjado existe una meticulosa red de control, un sistema nervioso que garantiza la integridad de toda la estructura. En España, el manual que rige estas normas es el Código Estructural. Este reglamento garantiza que la calidad y la seguridad no se dejan al azar, sino que son el resultado de un plan riguroso y sistemático.

Este artículo revela tres aspectos sorprendentes extraídos directamente de los procedimientos de este código. Son tres verdades sobre el control de calidad que cambiarán tu forma de ver los edificios que te rodean y demostrarán que, al igual que un rascacielos, la confianza se construye paso a paso y con una supervisión implacable.

1. El control se realiza mediante dos llaves: el constructor se autovigila y un supervisor lo supervisa.

En la construcción de una estructura, la responsabilidad no recae en una sola persona, sino en un sistema de doble verificación. Piénsalo como un sistema de doble llave, en el que se requieren dos validaciones para proceder. El Código Estructural establece un mecanismo de control con dos capas fundamentales que garantizan la máxima fiabilidad.

La primera capa es el «autocontrol» del constructor. La propia empresa constructora tiene la obligación de inspeccionar y registrar de forma sistemática la calidad de su trabajo. No es una opción, sino una exigencia. Deben seguir un plan de inspección y dejar constancia de que cada proceso cumple con las especificaciones del proyecto.

La segunda capa es el «control de contraste», que realiza una entidad independiente: la dirección facultativa (el equipo técnico de arquitectos e ingenieros que dirige la obra y actúa como supervisor en nombre del propietario y de la normativa). Este equipo no da por bueno el trabajo del constructor sin más, sino que realiza sus propias comprobaciones para verificar que el autocontrol se ha llevado a cabo correctamente y que los resultados son conformes.

Para comprender la rigurosidad de este sistema, veamos las frecuencias mínimas de inspección de un elemento como el pilar. Según las tablas de inspección del código, el constructor debe comprobar el 50 % de los pilares de un lote, mientras que la dirección facultativa debe realizar un control de contraste del 10 % de dichos pilares. Esta redundancia no es burocracia, sino una red de seguridad diseñada para que nada importante pase desapercibido. Esta redundancia deliberada no solo sirve para detectar errores, sino que forma parte de una filosofía pragmática que reconoce que, en proyectos de esta complejidad, la perfección es imposible, pero garantizar la corrección es posible.

2. La perfección no existe, pero la corrección sí: los errores forman parte del plan.

Podríamos pensar que el objetivo de un sistema de control tan estricto es evitar cometer errores, pero no es así. Sin embargo, la realidad de una obra es compleja y el Código Estructural adopta un enfoque más pragmático y eficaz: asume que se producirán desviaciones, pero exige un proceso robusto para detectarlas, documentarlas y corregirlas antes de que se conviertan en un problema.

Cada vez que una inspección detecta una «no conformidad» (un aspecto que no cumple con el proyecto), se registra en una «Ficha de registro de control». En esta ficha se detalla el problema y, lo más importante, la «decisión adoptada» para solucionarlo. Los ejemplos extraídos de un proyecto real son muy reveladores:

  • Ejemplo 1 (ficha n.º 6): durante una comprobación de cotas, se detectó que el pilar n.º 20 se había hormigonado 7,5 cm por encima de lo especificado. Un error así habría impedido la correcta colocación de las armaduras de acero del forjado superior. La solución fue directa y contundente: se ordenó demoler el hormigón sobrante hasta alcanzar la cota correcta.
  • Ejemplo 2 (ficha n.º 3): las barras de acero de espera de un pilar (es decir, las que conectan con el pilar del piso superior) estaban mal posicionadas. Esto comprometía el «recubrimiento», es decir, la capa mínima de hormigón que debe proteger el acero de la corrosión. En este caso, se hizo valer el criterio de ingeniería: en lugar de optar por la demolición, que habría supuesto un enorme coste y un retraso, se tomó una decisión más inteligente. Se aceptó la desviación dentro de las tolerancias y se ordenó modificar la forma final del pilar para garantizar el recubrimiento mínimo y salvar el elemento, sin comprometer en absoluto la seguridad.
  • Ejemplo 3 (ficha n.º 4): tras retirar el encofrado de un pilar, se observó una fisura horizontal. Aunque resultó alarmante a primera vista, demostró la importancia de un diagnóstico preciso. La inspección determinó que se trataba de una fisura superficial causada por el «asiento plástico» del hormigón fresco, un fenómeno conocido que no tiene impacto estructural. En lugar de provocar una alarma innecesaria, se aplicó una solución precisa: picar la zona afectada y repararla con un mortero especial.

Este enfoque sistemático de la gestión de errores es lo que construye la verdadera seguridad. No se trata de no cometer nunca un error, sino de tener un plan infalible para corregir cada uno de ellos y dejar un registro completo de cada decisión.

3. Lo que se llama «simplificado» resulta sorprendentemente complejo.

El Código Estructural ofrece una «opción simplificada» para el control de la ejecución en obras de edificación con ciertas características. El nombre puede engañar al sugerir un proceso más laxo o básico. Nada más lejos de la realidad.

Esta modalidad «simplificada» sigue siendo un método extraordinariamente metódico y riguroso. Para empezar, obliga a dividir toda la estructura en «lotes de ejecución». Un lote no es una división arbitraria, sino que está perfectamente definido. Por ejemplo, en el caso de pilares y forjados, un lote equivale a un máximo de 250 m² de superficie construida o dos plantas. De este modo, se asegura una inspección granular y manejable de la obra.

Para cada uno de estos lotes, se despliega un plan de inspección que abarca una larga lista de procesos de ejecución. No solo se comprueba si el hormigón se ha vertido correctamente, sino que el control abarca desde la «gestión de acopios» (verificar que los materiales que llegan a la obra son los correctos) y los «replanteos» (asegurar que cada elemento estructural se ubica en su posición exacta según los planos), hasta el «acabado» final de los elementos.

La clave es que en ingeniería estructural no hay atajos. Incluso el camino «simplificado» es un testimonio de una cultura en la que el rigor metodológico es el estándar mínimo para garantizar la seguridad pública.

Conclusión: una nueva mirada sobre las estructuras que nos rodean.

Detrás del hormigón y el acero que vemos tomar forma en una obra, existe una arquitectura invisible de procesos: una coreografía de comprobaciones, registros y correcciones planificadas. Este sistema nervioso invisible de control y corrección es lo que confiere resiliencia a un edificio, permitiéndole nacer conforme a las reglas más estrictas.

No se trata de la ausencia de errores, sino de la certeza de que se corregirán, lo cual nos da tranquilidad. La próxima vez que entres en un edificio, ¿te acordarás de la inmensa red de controles y decisiones de ingeniería que garantizan que el edificio se mantenga firme y seguro sobre tu cabeza?

En esta conversación se exponen varias ideas relacionadas con este tema.

Este vídeo condensa los puntos clave de la opción simplificada del control de calidad, tal y como se establece en el Código Estructural.

Aquí os dejo un resumen que creo que os puede ayudar, ya que os será de gran utilidad para resolver vuestras dudas.

Pincha aquí para descargar

La Fundación Musaat ofrece una monografía que podéis descargar a continuación, que creo que es muy útil para adentrarse en los entresijos del Código Estructural en relación con la opción simplificada del control de ejecución de estructuras de hormigón.

Pincha aquí para descargar

Curso:

Curso de fabricación y puesta en obra del hormigón.

Licencia de Creative Commons
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Cinco ideas revolucionarias de la «estrategia del océano azul» que cambiarán tu forma de ver los negocios.

Introducción: ¿Atrapado en un mar de competencia?

¿Sientes que tu negocio está en una lucha constante por la cuota de mercado? ¿Las guerras de precios y los márgenes de beneficio cada vez más reducidos marcan tu día a día? Si es así, es probable que estés navegando, por lo que los estrategas W. Chan Kim y Renée Mauborgne llaman un «océano rojo».

Esta metáfora describe el espacio de mercado conocido, donde las industrias y sus reglas del juego están perfectamente definidas. En estas aguas, las empresas compiten ferozmente por una demanda existente, tratando de superar a sus rivales para llevarse la mayor participación posible. A medida que el mercado se satura, la competencia a muerte tiñe el agua de sangre, dando lugar a un entorno de crecimiento limitado y utilidades decrecientes.

Pero ¿y si hubiera una alternativa? ¿Y si, en lugar de luchar por un trozo del pastel, pudieras crear uno completamente nuevo? Esa es la promesa del «océano azul»: la creación de espacios de mercado sin competencia, donde aún no existen las reglas del juego y la demanda se crea en lugar de disputarse.

A continuación, te presentamos las cinco ideas más impactantes del libro La estrategia del océano azul, que ofrecen un método sistemático para salir del océano rojo y navegar hacia un crecimiento rentable y sostenible.

1. Olvida a tus rivales: el objetivo es que la competencia sea irrelevante.

La primera idea puede resultar sorprendente: el objetivo de una buena estrategia no es vencer a la competencia, sino hacerla irrelevante. Mientras que la estrategia convencional se centra en la referenciación (benchmarking) y en superar a los rivales, la estrategia del océano azul propone un cambio de enfoque radical.

El contraste, basado en los principios del libro, es claro:

  • Estrategia del Océano Rojo:
    • Competir en el espacio existente del mercado.
    • Vencer a la competencia.
    • Explotar la demanda existente.
    • Elegir entre la disyuntiva entre valor y coste.
    • Alinear todo el sistema de las actividades de una empresa con la decisión estratégica de la diferenciación o del bajo costo.
  • Estrategia del Océano Azul:
    • Crear un espacio sin competencia en el mercado.
    • Hacer que la competencia pierda toda importancia.
    • Crear y capturar nueva demanda.
    • Romper la disyuntiva entre valor y coste.
    • Alinear todo el sistema de las actividades de una empresa con el propósito de lograr diferenciación y bajo costo.

Este cambio de mentalidad se resume a la perfección en una de las frases más célebres del libro:

«La única manera de vencer a la competencia es dejar de tratar de vencerla».

Estratégicamente, este giro es poderoso porque desplaza el objetivo empresarial de un juego de suma cero, en el que la ganancia de una empresa es la pérdida de otra, a una lógica de creación de nuevo valor. En lugar de repartir una demanda limitada, el objetivo es aumentar el tamaño total del mercado.

2. Innovación en valor: el arte de ser diferente y más barato a la vez.

El pensamiento estratégico tradicional nos ha enseñado que las empresas deben tomar una decisión fundamental: o bien compiten por diferenciación, ofreciendo un mayor valor a un coste más alto, o bien compiten por bajo coste, ofreciendo un valor razonable a un coste menor. La estrategia de los océanos azules rompe esta disyuntiva con su piedra angular: la innovación en valor.

La innovación en valor consiste en buscar simultáneamente la diferenciación y el bajo coste. No se trata de un simple avance tecnológico o de ser el primero en un mercado, sino de alinear la innovación con la utilidad para el comprador, el precio y la estructura de costes de la empresa.

Este concepto se materializa cuando se cuestiona en qué compite la industria. Al eliminar o reducir las variables que los clientes no valoran o que suponen un alto coste, la empresa consigue una estructura de costes inferior a la de sus competidores. Del mismo modo, al incrementar y crear nuevas fuentes de valor que la industria nunca antes había ofrecido, se genera una diferenciación radical. Es esta doble acción la que rompe la disyuntiva clásica y permite ofrecer un valor superior a un coste menor.

Este enfoque, que busca la diferenciación y el bajo coste de forma simultánea, no es solo una teoría elegante, sino que tiene un impacto medible y desproporcionado en los resultados del negocio, como demuestran las cifras del siguiente apartado.

3. El impacto real de los océanos azules (traducido en cifras).

Para quienes puedan pensar que crear nuevos mercados es una apuesta demasiado arriesgada, los autores presentan los resultados de un estudio sobre 108 lanzamientos de negocios que demuestran lo contrario. Los resultados son sorprendentes y revelan una clara asimetría entre el riesgo y la recompensa.

Las cifras hablan por sí solas:

  • Lanzamientos en océanos rojos (el 86 % del total) generaron solo el 62 % de los ingresos totales y un escaso 39 % de las utilidades.
  • Lanzamientos en océanos azules (14 % del total): generaron el 38 % de los ingresos y un impresionante 61 % de las utilidades totales.

Esta asimetría demuestra que, aunque la creación de océanos azules es menos frecuente, su impacto en la rentabilidad es desproporcionadamente alto. Aunque navegar en aguas competitivas puede parecer la opción más segura, las cifras indican que la verdadera oportunidad de crecimiento y rentabilidad se halla en la creación de nuevos espacios de mercado. Por tanto, la búsqueda de océanos azules se convierte en un imperativo estratégico.

4. Deja de obsesionarte con tus clientes y empieza a pensar en los «no clientes».

Las empresas tienden a centrarse en sus clientes actuales, tratando de segmentar el mercado de manera cada vez más precisa para satisfacer mejor sus preferencias. Para crear un océano azul y maximizar su tamaño, la estrategia propone hacer lo contrario: mirar más allá de la demanda existente y centrarse en los «no clientes».

Los autores identifican tres niveles de «no clientes» que representan un torrente de demanda potencial sin explotar:

  • Primer nivel: Personas que están próximas a convertirse en no clientes. Utilizan mínimamente la oferta actual mientras buscan algo mejor y están a la espera de dejar de ser clientes.
  • Segundo nivel: No clientes que rechazan conscientemente el mercado de la empresa. Han visto la oferta y han decidido no utilizarla.
  • Tercer nivel: No clientes inexplorados que jamás han contemplado la oferta de la empresa como una opción.

El caso del vino australiano Yellow Tail es un ejemplo perfecto. En lugar de competir con los conocedores del vino, se centraron en los no clientes: los bebedores de cerveza y cócteles. Este grupo se sentía intimidado por los aspectos del vino tradicional, como la compleja terminología enológica, el envejecimiento, los taninos y la sofisticación que rodeaba su consumo. Al identificar estos puntos de fricción, Yellow Tail creó un vino fácil de beber, accesible y divertido que eliminó o redujo sistemáticamente esas barreras, creando en su lugar «facilidad para beber» y «diversión y aventura», y abrió un océano azul masivo al convertir a los no bebedores de vino en nuevos clientes.

5. La herramienta para reconstruir tu mercado: eliminar, reducir, incrementar y crear.

La estrategia del océano azul no es un concepto abstracto, sino un proceso práctico y sistemático. Su principal herramienta para aplicar la innovación en valor es el esquema de las cuatro acciones, que desafía la lógica estratégica de una industria a través de cuatro preguntas clave:

  • ¿Qué variables que la industria da por sentadas se deben eliminar?
  • ¿Qué variables se deben reducir muy por debajo de la norma de la industria?
  • ¿Qué variables se deben incrementar muy por encima de la norma de la industria?
  • ¿Qué variables se deben crear porque la industria nunca las ha ofrecido?

El ejemplo más paradigmático es el Cirque du Soleil. En una industria del circo en declive, aplicaron este modelo para reinventar el entretenimiento en vivo.

  • Eliminó: las estrellas del circo, los espectáculos con animales, las concesiones en los pasillos y las pistas múltiples.
  • Redujo: la diversión, el humor, el suspense y el peligro.
  • Incrementó: un único escenario.
  • Creó: un tema, un ambiente refinado, múltiples producciones y música y danza artísticas.

Esta herramienta sistemática permite a cualquier empresa deconstruir la lógica de su sector y reconstruirla en una nueva curva de valor. Al responder a estas cuatro preguntas, una empresa puede visualizar un nuevo perfil estratégico que la diferencie radicalmente de la competencia, de modo que la comparación directa pierda sentido.

Conclusión: ¿cuál es tu océano azul?

La estrategia del océano azul es mucho más que una teoría empresarial: supone un cambio de mentalidad fundamental. Nos invita a pasar, de competir a crear, de dividir los mercados existentes a construirlos de nuevo. Demuestra que la creación de estos nuevos espacios no es fruto de la suerte o la genialidad, sino el resultado de un proceso estratégico, analítico y sistemático que cualquier organización puede llevar a cabo.

La próxima vez que te sientas atrapado en las sangrientas aguas de la competencia, detente y hazte una pregunta: ¿qué reglas «inquebrantables» de tu sector podrías empezar a cuestionar hoy mismo para descubrir tu propio océano azul?

En este audio se mantiene una conversación interesante sobre este tema.

El siguiente vídeo sintetiza bien las ideas más importantes de la estrategia del océano azul.

Os dejo un vídeo de Polimedia en el que el profesor Jordi Joan Mauri Castelló nos explica este concepto. Espero que os resulte útil.

Licencia de Creative Commons
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

El diagrama causa-efecto: herramienta fundamental para entender y mejorar procesos

Un diagrama de causa y efecto es una representación visual compuesta por líneas y símbolos que muestra claramente la relación entre un efecto (o problema) y sus posibles causas. A este tipo de representación también se le conoce como diagrama de Ishikawa o diagrama de espina de pescado, debido a su semejanza con el esqueleto lateral de un pez. El efecto se coloca a la derecha (como la «cabeza» del pez), mientras que las causas principales se disponen a la izquierda, ramificándose desde un eje central y subdividiéndose en causas menores.

Origen y fundamento

El primer diagrama fue desarrollado en 1943 por Kaoru Ishikawa, un químico industrial japonés y profesor de la Universidad de Tokio, pionero del control de calidad en Japón. Aunque el concepto básico existía desde los años veinte, Ishikawa lo perfeccionó, sistematizó y popularizó como una de las siete herramientas básicas de control de calidad.

Propósito y funcionamiento

La utilidad principal del diagrama es investigar efectos —ya sean «malos», para corregirlos, o «buenos», para entender qué causas los propician—, reconociendo que un efecto puede provenir de múltiples causas a distintos niveles de profundidad. Generalmente, se organiza en categorías como métodos de trabajo, materiales, medición, personal, ambiente y, a veces, administración o mantenimiento, de donde surgen causas secundarias (por ejemplo, subcategorías bajo «métodos» como capacitación o características físicas del personal).

Paso a paso para elaborarlo

  1. Definir el efecto o problema de calidad y colocarlo a la derecha del pliego o en la «cabeza» del diagrama.
  2. Dibujar el eje principal (espina) y, de sus costados, los huesos principales que representan categorías de causas (p. ej., 6 M: método, máquina, mano de obra, materiales, medición, medio ambiente).
  3. Identificar causas secundarias mediante una sesión de lluvia de ideas (brainstorming) en equipo, aprovechando el pensamiento creativo y evitando juicios prematuros.
  4. Subdividir cada causa principal en causas menores (a partir de preguntas como «¿por qué?», «¿qué?», o «¿quién?»).
  5. Cuando se agotan las ideas, se inicia una sesión de evaluación, donde cada miembro vota por las causas menores más probables; las más votadas se destacan y se priorizan (normalmente cuatro o cinco).
  6. Se proponen soluciones, evaluadas según criterios como costo, factibilidad o resistencia al cambio; una vez acordadas, se implementan, se prueban y el diagrama se actualiza y coloca en lugares visibles para consulta continua.

Claves para hacer más eficaz la lluvia de ideas

  • Asegurar una participación equitativa: cada miembro recomienda ideas por turno; si alguien no tiene, pasa, pero puede retomarlas después.
  • Promover cantidad sobre calidad: las ideas «tontas» pueden desencadenar las mejores soluciones.
  • Evitar las críticas durante la generación de ideas y hacer una evaluación posterior.
  • Utilizar un papel grande (por ejemplo, de 60 x 90 cm), visible y pegado en la pared para fomentar la participación.
  • Fomentar una atmósfera enfocada en soluciones, no en quejas; el líder guía con preguntas clave.
  • Dejar incubar las ideas (por ejemplo, una noche) y luego retomarlas con más estímulos creativos.

Aplicación y beneficios estratégicos

El diagrama tiene aplicaciones casi ilimitadas, desde la fabricación, la investigación y las ventas hasta las oficinas, la educación, la sanidad, etc. Entre sus principales usos destacan:

  1. Mejorar la calidad del producto o servicio, optimizar recursos y reducir costos.
  2. Detectar y eliminar causas de no conformidades o quejas del cliente.
  3. Estandarizar procesos actuales y propuestos.
  4. Formar y entrenar al personal en toma de decisiones y acciones correctivas.

Tipos de diagramas relacionados

Además del tipo más común (enumeración de causas), existen variantes como:

  • Diagrama de dispersión: se trabaja completamente una rama antes de pasar a otra, para investigar la variabilidad.
  • Diagrama de proceso: cada paso del proceso (como carga, corte, ensamblado) se usa como causa principal, útil para procesos operativos o continuos.

Conclusión

El diagrama causa-efecto o diagrama de Ishikawa es una herramienta visual muy potente para representar y comprender cómo múltiples causas contribuyen a un efecto determinado. Su valor reside en su estructura clara, su enfoque sistemático, su aplicación colaborativa y su versatilidad. Su eficacia depende de una elaboración rigurosa, que incluye desde la definición precisa del problema hasta la evaluación participativa y la implementación de soluciones, pasando por el uso estratégico de la lluvia de ideas. Todo ello, junto con su capacidad de adaptación a diferentes contextos, lo convierte en una metodología viva y útil para la enseñanza, la industria y la gestión.

Os dejo varios vídeos de esta técnica.

Referencias:

Cursos:

Curso de gestión de costes y producción de la maquinaria empleada en la construcción.

Licencia de Creative Commons
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

El diagrama de Pareto en ingeniería: teoría, aplicaciones y ejemplos prácticos

Figura 1. Diagrama de Pareto

1. Introducción.

En el ámbito de la ingeniería y la gestión de la calidad, el diagrama de Pareto se ha consolidado como una herramienta esencial para la toma de decisiones y la mejora continua. Permite identificar los problemas más importantes, priorizar acciones y optimizar el uso de recursos.

La idea central se basa en la observación de que unos pocos factores tienen un impacto desproporcionado en los resultados, lo que se conoce como el principio 80/20. Por ejemplo, en una obra de construcción, unos pocos materiales concentran la mayor parte del coste, mientras que, en logística, unos pocos clientes generan la mayoría de las ventas.

Figura 2. Vilfredo Pareto (1848-1923). https://es.wikipedia.org/

2. Origen histórico

El concepto fue acuñado por el economista italiano Vilfredo Pareto (1848-1923), quien observó que aproximadamente el 80 % de la riqueza en Europa estaba en manos del 20 % de la población.

Décadas más tarde, el ingeniero y consultor de calidad Joseph M. Juran reconoció la aplicabilidad universal de esta distribución y acuñó la expresión «los pocos vitales y los muchos triviales (o útiles)», extendiendo su uso a la gestión empresarial y de calidad.

3. ¿Qué es un diagrama de Pareto?

Es un gráfico de barras en el que los datos se clasifican de mayor a menor importancia, de izquierda a derecha. Cada barra representa una categoría (por ejemplo, defectos, causas de fallo o tipos de no conformidades).

A menudo, se añade una línea de porcentaje acumulado que muestra qué porcentaje del problema total explican las categorías principales.

La diferencia con respecto a un histograma es clara: en el diagrama de Pareto, el eje horizontal representa categorías, mientras que en el histograma representa intervalos numéricos.

Figura 3. Diagrama de Pareto – Defectos en prefabricados de hormigón

4. Construcción paso a paso.

El procedimiento clásico consta de seis pasos:

  1. Determinar cómo clasificar los datos (problemas, causas, defectos, costes, etc.).
  2. Definir la métrica (frecuencia, valor monetario o frecuencia ponderada).
  3. Recolectar datos en un periodo adecuado.
  4. Agrupar y ordenar las categorías en orden descendente.
  5. Calcular el porcentaje acumulado.
  6. Dibujar el diagrama y distinguir cuáles son los pocos vitales.

Cuando se emplea el porcentaje acumulado, este debe coincidir con la escala principal para que el 100 % se sitúe a la misma altura que la suma de frecuencias o valores.

5. Importancia en la mejora continua.

El diagrama de Pareto no es un análisis estático, sino un proceso cíclico.

  • En la primera iteración, se identifican las categorías más críticas.
  • Tras actuar sobre ellas, un nuevo análisis muestra otras prioridades.
  • El ciclo se repite hasta que los problemas se vuelven residuales o insignificantes.

Este enfoque garantiza que los recursos se destinen a lo que realmente afecta a la calidad, la productividad o los costes.

6. Aplicaciones prácticas

Ingeniería civil: defectos en prefabricados de hormigón.

En una planta de prefabricados, se recopilaron datos sobre los defectos.

  • Fisuras: 120
  • Huecos: 80
  • Desconchados: 45
  • Dimensiones incorrectas: 30
  • Color defectuoso: 25
  • Otros: 20

El análisis de la Figura 3 muestra que las fisuras y los huecos representan más del 65 % de los defectos totales, por lo que constituyen los «puntos vitales» en los que hay que centrarse para mejorar.

Logística: gestión de inventarios en obra (análisis ABC).

En el suministro de materiales de construcción, el análisis Pareto se traduce en el método ABC (Figura 4).

Para ello se clasifican según su valor de uso anual (podría ser cualquier otro periodo), agrupándolos de acuerdo con el coste de su gasto anual: cantidad utilizada (consumida, vendida, empleada, etc.) coste unitario (o precio unitario). Para ello se dividen los elementos en tres grupos:

  • Grupo A: Suponen un porcentaje alto de la inversión total, de forma que, controlando este grupo, se tiene controlado casi todo el almacén. Representa generalmente el 10 % de los artículos, estando su valor de uso entre el 60 % y el 80 % del total.
  • Grupo C: Son aquellos cuyo control es poco interesante, pues siendo muy numeroso, su valor es pequeño. Suele ser el 50-70 % del total de artículos, significando solo entre el 5-10 % del valor total de uso
  • Grupo B: Tienen una importancia en relación con el número de unidades del almacén parecida a la que tienen con referencia al valor total de la inversión del inventario. Abarca generalmente al 25 % de los artículos, y representa entre el 15-30 % del valor total de uso.
Figura 4. Método ABC para gestionar los inventarios

Por ejemplo:

  • Acero estructural: 40 000 €
  • Cemento: 30 000 €
  • Tuberías PVC: 12 000 €
  • Pintura: 6 000 €
  • Clavos y tornillería: 2 000 €
  • Otros: 1 000 €

La Figura 5 muestra que el acero y el cemento (el 20 % de los artículos) representan el 70 % del valor total. Estos materiales requieren un control de inventario estricto, mientras que los de bajo impacto se gestionan de manera más flexible.

Figura 5. Diagrama de Pareto – Inventario en obra

6.3 Otras aplicaciones destacadas.

  • Quejas de clientes: un pequeño grupo de problemas genera la mayoría de las reclamaciones.
  • Procesos productivos: unos pocos defectos causan la mayor parte de los reprocesos.
  • Mantenimiento: unas pocas averías originan la mayor parte del tiempo de inactividad.
  • Ventas: unos pocos clientes concentran la mayor parte de los ingresos.

7. Conclusión

El diagrama de Pareto es sencillo de apariencia, pero potente en resultados.

  • Facilita la visualización de las prioridades.
  • Permite concentrar los recursos en lo más importante.
  • Puede aplicarse en ingeniería civil, logística, producción, calidad, marketing y gestión empresarial.

La clave está en identificar los aspectos vitales y no dispersar esfuerzos en los triviales.

Os dejo algunos vídeos al respecto.

Referencias:

Cursos:

Curso de gestión de costes y producción de la maquinaria empleada en la construcción.

Licencia de Creative Commons
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Guía para las especificaciones técnicas del hormigón

El documento, titulado «Guía para las especificaciones técnicas del hormigón», forma parte de la serie de guías Eurocódigos, elaborada por el Ministerio de Transportes, Movilidad y Agenda Urbana de España. Su propósito es proporcionar un marco de referencia que facilite la aplicación de los Eurocódigos en el diseño y ejecución de obras de construcción, prestando especial atención al hormigón. A lo largo del texto se abordan aspectos técnicos relacionados con la especificación del hormigón, con el objetivo de garantizar el cumplimiento de las normativas europeas y de las exigencias del Código Estructural español.

La guía se enmarca en un contexto normativo que ha experimentado una notable transformación desde la implementación de los Eurocódigos en la década de 1980. Se destaca la importancia de estas normativas para armonizar los criterios de diseño y ejecución en el ámbito de la construcción en Europa. La guía se presenta como un recurso esencial para los profesionales del sector, ya que proporciona directrices claras y concisas sobre cómo especificar el hormigón de acuerdo con la normativa vigente.

Desarrollo de los aspectos más relevantes

La guía se organiza en varios capítulos que abordan desde la introducción a los Eurocódigos hasta la definición de especificaciones técnicas del hormigón. En el primer capítulo se establece el contexto y la importancia de la normativa europea en el ámbito de la construcción, y se destaca la evolución de los Eurocódigos desde su creación hasta su aplicación en proyectos de infraestructura en España. Se menciona que la serie de guías Eurocódigos se inició en 2018 con el objetivo de profundizar en el conocimiento de estas normativas en la comunidad técnica española y facilitar su aplicación en proyectos de la Dirección General de Carreteras.

Uno de los aspectos más relevantes es la definición de los requisitos básicos para especificar el hormigón, que incluyen la clase de resistencia a compresión, la clase de exposición y el tamaño máximo del árido. Estos requisitos son esenciales para garantizar que el hormigón utilizado en las obras cumpla con las propiedades mecánicas y de durabilidad necesarias para su correcto funcionamiento en las condiciones ambientales previstas. La guía detalla cómo se deben designar los hormigones y cómo se debe elaborar el cuadro de especificaciones técnicas para garantizar el cumplimiento de las normativas.

La guía también aborda la equivalencia entre las especificaciones del hormigón según los Eurocódigos y el Código Estructural, y proporciona un marco claro para interpretar y aplicar ambas normativas. Este enfoque permite a los profesionales del sector entender cómo se relacionan los requisitos de cada norma y cómo se pueden aplicar en la práctica. Se hace hincapié en la necesidad de resolver la compatibilidad entre las normas europeas de producto, ejecución y control, y el Código Estructural, motivo por el cual se ha elaborado esta guía.

Además, se incluyen recomendaciones sobre el control de calidad y la ejecución del hormigón, haciendo hincapié en la importancia de establecer niveles de control adecuados durante la producción y colocación del material. La guía sugiere que el control de conformidad de la resistencia del hormigón se realice mediante métodos estadísticos, lo que permite evaluar con mayor precisión la calidad del material utilizado en las obras. Se menciona que el control de conformidad debe incluir la verificación de la resistencia, durabilidad y otras características exigidas en el pliego de prescripciones técnicas particulares.

Otro aspecto destacado es la clasificación del hormigón en función de su tipo y función estructural. La guía establece que es conveniente incluir una distinción en función del uso previsto del hormigón, diferenciando entre hormigón en masa, hormigón armado, hormigón pretensado y hormigón no estructural. Esta clasificación permite prever las características del material definidas en la especificación, lo que es esencial para garantizar la calidad y durabilidad del hormigón en las obras.

La guía también proporciona un análisis detallado de los requisitos adicionales que pueden incluirse en la especificación del hormigón, como el tipo de cemento, la temperatura del hormigón fresco y las características exigidas para resistir daños por ciclos de hielo-deshielo. Estos requisitos adicionales son importantes para garantizar que el hormigón se adapte a las condiciones específicas del entorno en el que se utilizará, lo que contribuirá a su durabilidad y rendimiento a largo plazo.

Recomendaciones prácticas

Para aplicar correctamente las especificaciones técnicas del hormigón, se recomienda que los estudiantes y los profesionales del sector se familiaricen con los Eurocódigos, el Código Estructural y la guía en cuestión. Se recomienda realizar capacitaciones periódicas sobre las normativas vigentes, ya que esto contribuirá a una mejor comprensión de los requisitos y a su correcta implementación en proyectos de construcción.

Asimismo, se sugiere establecer protocolos claros para el control de calidad del hormigón que incluyan la realización de ensayos de resistencia y durabilidad en diferentes etapas del proceso de producción y colocación. La documentación de estos ensayos debe ser rigurosa y accesible para facilitar la trazabilidad del material utilizado en las obras.

Es fundamental fomentar la colaboración entre todos los actores involucrados en el proceso constructivo, desde los diseñadores hasta los ejecutores, para garantizar que todos comprendan y apliquen adecuadamente las especificaciones técnicas del hormigón. La comunicación efectiva entre los equipos de trabajo puede ayudar a prevenir errores y garantizar el cumplimiento de los estándares de calidad establecidos.

Conclusión

La guía de especificaciones técnicas del hormigón proporciona un marco detallado y estructurado que facilita la aplicación de normativas europeas en el ámbito de la construcción en España. Su contenido técnico y práctico resulta muy útil para el alumnado y los profesionales del sector, ya que facilita la comprensión de los requisitos necesarios para garantizar la calidad y durabilidad del hormigón en las obras. La aplicación de las recomendaciones propuestas mejorará la práctica constructiva y garantizará el cumplimiento de las normativas vigentes.

A continuación, os paso la guía completa. Espero que os sea útil.

Pincha aquí para descargar

Curso:

Curso de fabricación y puesta en obra del hormigón.

Una playa sostenible, ¿con duchas o con lavapiés de agua de mar?

Figura 1. Lavapiés ecológicos en la Comunitat Valenciana. Fotografía: V. Yepes

¿Es sostenible desde el punto de vista ambiental tener duchas con agua potable en nuestras playas? ¿Sería mejor la opción de unos lavapiés que utilizaran el agua del mar? Este es un tema que tuvo cierto debate en la Comunidad Valenciana y en el que, en su día, participé en su solución. De hecho, el agua que se consume en las playas valencianas con duchas era equivalente al consumo diario de agua potable de una ciudad de 80.000 habitantes (Yepes, 2005).

Sin embargo, el problema no es sencillo desde el punto de vista ingenieril, pues se debe asegurar la correcta captación del agua, su desinfección y el control de un sistema que, a todas luces, debe ser desmontable al situarse en una zona del dominio público. Además, el sistema se debe monitorizar para atender cualquier avería en el mínimo tiempo posible.

Pero, así y todo. ¿Son obligatorias las duchas de agua potable en las playas que quieran certificarse con algún distintivo de calidad? ¿Qué ocurre si se quiere remodelar un paseo marítimo y se quieren aplicar los fondos Next Generation de la Unión Europea? ¿Se pueden considerar las duchas como sostenibles? ¿En qué consiste su alternativa de lavapiés ecológicos? Os lo voy a intentar explicar en un vídeo que os he preparado.

Figura 2. Pantallazo del control telemático de los lavapiés ecológicos en la Comunitat Valenciana.

Os presento aquí un vídeo que preparé para un curso sobre gestión de playas. Este curso es una ampliación respecto a algunos cursos presenciales que he tenido la oportunidad de dirigir, el último, en Oporto (Portugal). En este caso, trata de la frecuentación y capacidad de carga de las playas. Espero que sea de vuestro interés.

También os dejo una conferencia que ofrecí, hace ya algún tiempo, donde hablaba de algunos de estos temas. Espero que siga vigente su contenido.

Pincha aquí para descargar

Licencia de Creative Commons
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Libro electrónico: Gestión de playas, del concepto a la práctica

Tengo el placer de compartir la versión electrónica, de libre acceso, de un libro en el que he tenido la oportunidad de participar en uno de sus capítulos: “Gestão de praias: do conceito à prática”. El libro ha sido publicado por el Instituto de Estudos Avançados da Universidade de São Paulo (Brasil). Los editores de este libro han sido los profesores Briana Bombana (Universitat Autònoma de Barcelona), Alexander Turra (Universidade de São Paulo, Instituto Oceanográfico) y Marcus Polette (Universidade do Vale do Itajaí).

Esta colección reúne textos que detallan algunos de los principales conceptos, perspectivas y prácticas sobre la gestión y la gobernanza de las playas. El libro deja claro el mensaje sobre la importancia ecosistémica de la playa, considerando sus atributos económicos, sociales, ambientales y culturales, y demuestra también que la playa depende de una gestión compleja que involucra el marco institucional federativo, que interviene en el saneamiento básico, la gestión de residuos sólidos, la gestión ambiental, la gestión costera y marina, y el ordenamiento territorial en las dimensiones urbana y rural. Cada una de estas interfaces se desarrolla con datos, información técnica y reflexiones científicas. Así pues, la presente obra es una excelente referencia sobre el estado del conocimiento de las playas. Cabe destacar que los organizadores proponen una agenda de investigación, clarifican los retos y las posibilidades para el avance del conocimiento sobre el tema e invitan a los lectores, independientemente de su origen científico, a una reflexión crítica sobre la sostenibilidad en el uso de los recursos marinos.

El libro podéis descargarlo gratuitamente en esta dirección: https://www.livrosabertos.sibi.usp.br/portaldelivrosUSP/catalog/book/920.

En este libro he tenido la oportunidad de escribir el capítulo 14: Gestión de playas en España. Aunque está en portugués, creo que es fácil de leer. Os dejo el capítulo para que podáis descargarlo.

Referencia:

YEPES, V. (2022). Gestão de praias na Espanha, in BOMBANA, B.; TURRA, A.; POLETTE, M. (Eds.): Gestão de praias: do conceito à prática. Instituto de Estudos Avançados da Universidade de São Paulo, pp. 360-381, São Paulo (Brazil). ISBN 978-65-87773-36-0. DOI 10.11606/9786587773360

Pincha aquí para descargar