Categoría: errores

La magia de la síntesis: cómo ordenar el caos de tus datos

Introducción: El dilema del exceso de información.

Imagine que se encuentra frente a una base de datos con cientos de columnas que detallan cada aspecto de su actividad. A primera vista, parece un tesoro, pero en la práctica, tener «demasiada» información a menudo paraliza la toma de decisiones. El ruido de los datos irrelevantes y la redundancia de variables que dicen esencialmente lo mismo ocultan las tendencias estratégicas reales.

Es aquí donde el análisis de componentes principales (PCA) resulta indispensable. Más que una técnica estadística de análisis multivariante, el PCA actúa como un «traductor inteligente» que simplifica la complejidad. Su función es transformar el caos de variables correlacionadas en un conjunto claro de factores que revelan la estructura real de su negocio.

 

Punto 1: Menos es más (la simplificación inteligente).

La esencia del PCA radica en la reducción de la dimensionalidad. En lugar de intentar procesar 20 variables que fluctúan juntas, esta técnica las sintetiza en un nuevo subconjunto de «factores» independientes.

Simplificar no implica pérdida de información. En el mundo del análisis de datos, simplificar significa ganar claridad. Al eliminar la redundancia, el PCA nos permite centrarnos en las fuerzas subyacentes que realmente marcan la diferencia. Como establece un principio fundamental del análisis multivariante:

«El exceso de variables dificulta el análisis de la información y genera redundancia; el PCA examina la interdependencia para reducir la dimensión a variables no observables».

Punto 2: La regla del 80 %. ¿Cuándo es «suficiente» información?

Para un estratega de datos, el rigor matemático debe equilibrarse con la utilidad práctica. ¿Cuánta información debemos conservar para que el modelo refleje fielmente la realidad? Las fuentes técnicas dictan criterios claros basados en la varianza explicada acumulada:

  • El mínimo académico: en ciertos contextos, explicar el 60 % de la varianza constituye el umbral básico aceptable.
  • Propósitos descriptivos: para entender las tendencias generales, suele bastar con alcanzar el 80 %.
  • Análisis predictivos: si los componentes se integran en modelos de machine learning posteriores, se recomienda capturar al menos el 90 %.
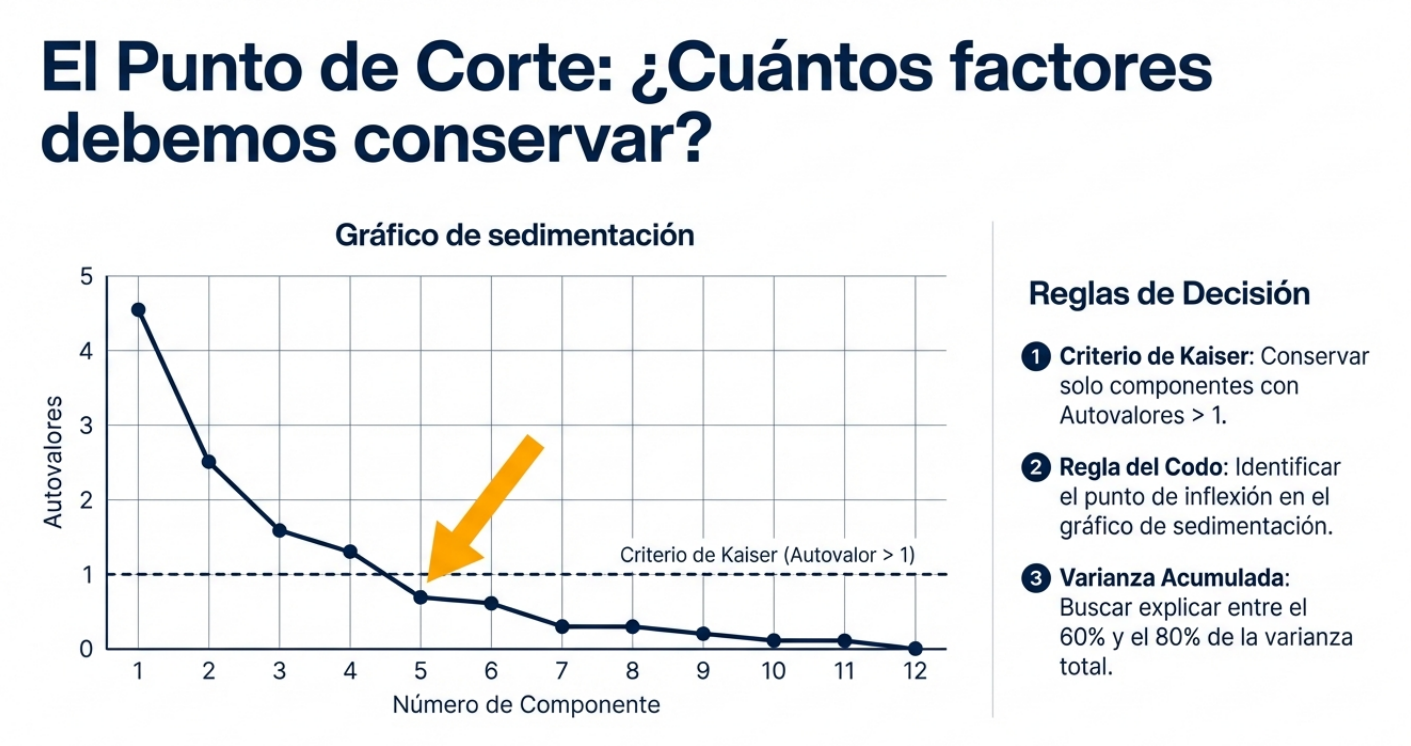
  • Criterio de Kaiser: establece que, para ser eficientes, solo se deben conservar los componentes con autovalores superiores a 1. Si un componente no explica más variación que una sola variable original, se trata de ruido estratégico y debe descartarse.

Punto 3: descubriendo variables «invisibles».

El PCA puede revelar estructuras que no existen en ninguna columna específica, pero que rigen el sistema. Para descubrir estas estructuras «invisibles», primero debemos decidir matemáticamente dónde termina la señal y dónde empieza el ruido.

Veamos dos ejemplos del mundo real presentes en los materiales de análisis:

  • Estabilidad financiera: al analizar variables como ingresos, educación, edad, empleo y ahorros, el PCA permite agruparlas en una dimensión principal denominada «estabilidad financiera a largo plazo». Asimismo, las deudas y las tarjetas de crédito pueden consolidarse en un factor denominado «historial crediticio».
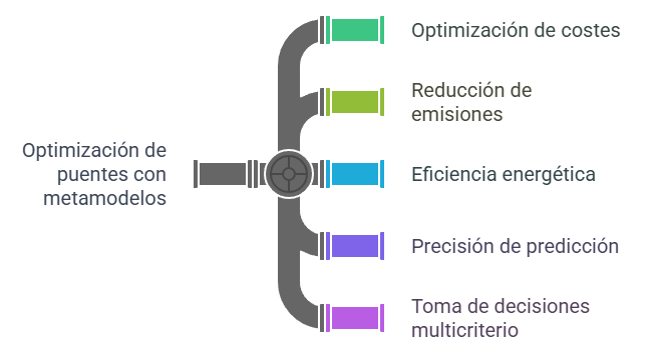
  • Ingeniería de puentes: En un estudio de 61 puentes de losa, variables técnicas como la luz principal y el canto del tablero se fusionan matemáticamente para definir la «proporción geométrica» de la estructura, mientras que la armadura activa y el hormigón definen su «capacidad estructural».

El PCA nos permite dejar de ver filas de números y empezar a ver conceptos abstractos y accionables.

Punto 4: Gráfico de sedimentación. La «luz» en el camino.

Para evitar la subjetividad, el analista confía en el gráfico de sedimentación. Esta herramienta visual ordena los autovalores de mayor a menor y muestra una caída que finalmente se estabiliza.

La clave está en identificar el «punto de inflexión» o el «codo» de la gráfica. Los componentes que se encuentran en la pendiente pronunciada, antes de que la curva se transforme en una línea plana (la zona de sedimentación), son los que contienen la esencia de los datos. Este método garantiza que la reducción se base en la evidencia y no en la intuición.

Punto 5: El «giro» necesario (la potencia de la rotación).

Un resultado inicial de PCA puede ser técnicamente correcto, pero «estratégicamente inútil» si las variables originales tienen pesos similares en varios componentes. Es como mirar una imagen desenfocada.

La solución es la rotación (específicamente, el método Varimax con normalización de Kaiser). Este ajuste matemático redistribuye las cargas para que cada variable original se asocie claramente a un único factor. La rotación no altera la información, sino que «ajusta la lente» para que la interpretación de cada dimensión sea nítida, lo que permite a los interesados comprender exactamente qué significa cada componente.

Punto 6: Rigor técnico y tamaño de la muestra.

El PCA no es un acto de magia, sino que requiere cimientos sólidos. La efectividad de la técnica depende de la presencia de correlaciones significativas (superiores a 0,3) y de contar con una muestra representativa. Desde el punto de vista académico, se exige un mínimo de 5 observaciones por variable, aunque el ratio óptimo es de 10 a 1.

Además, la validez de una carga factorial depende directamente del tamaño de la muestra, como se detalla en la siguiente escala de rigor:

Tamaño de la muestra Carga factorial mínima requerida
350 observaciones 0,30
200 observaciones 0,40
150 observaciones 0,45
120 observaciones 0,50
100 observaciones 0,55
85 observaciones 0,60
70 observaciones 0,65
60 observaciones 0,70
50 observaciones 0,75

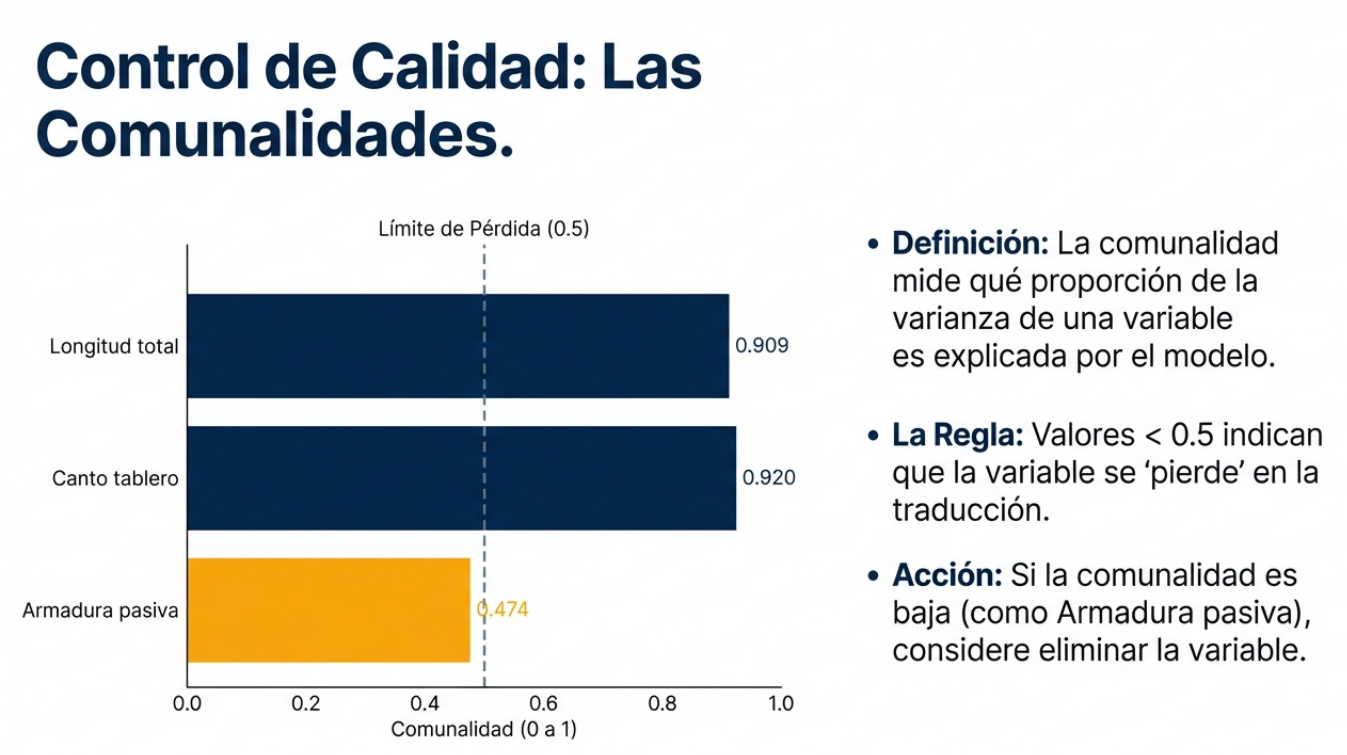
Un paso crítico final es el análisis de las comunalidades. Si una variable tiene una comunalidad inferior a 0,5, significa que el modelo no logra explicar su varianza de manera satisfactoria. En términos estratégicos, esa variable se considera «carente de explicación» y debería eliminarse para no contaminar el análisis.

Conclusión: mirando al futuro de tus datos.

El análisis de componentes principales es una pieza angular de la preparación de datos. Al eliminar el ruido, preparamos el terreno para técnicas avanzadas de aprendizaje automático, como el agrupamiento o la predicción, que funcionan con mayor agilidad sobre datos sintetizados.

En un mercado saturado de información, la ventaja competitiva pertenece a quienes logran destilar el conocimiento. ¿Cómo cambiaría su visión estratégica si pudiera reducir sus 100 indicadores de rendimiento a solo tres dimensiones maestras que realmente explicaran el éxito de su organización?

Este vídeo puede servirles para introducir las ideas más importantes.

En esta conversación puedes escuchar las ideas más interesantes sobre este tema.

El vídeo sintetiza bien lo más importante del análisis de componentes principales.

PCA_Strategic_Clarity

Licencia de Creative Commons
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

El arte de predecir lo invisible: claves para entender la inferencia estadística

¿Cómo podemos determinar la intención de voto de toda una nación o evaluar la eficacia de un nuevo fármaco sin entrevistar a todos los ciudadanos ni tratar a todos los pacientes del planeta? En nuestra vida cotidiana, nos enfrentamos constantemente al reto de tomar decisiones globales basadas en información limitada. Medir el total de elementos suele ser física o económicamente inviable.

Como expertos en comunicación de datos, consideramos la inferencia estadística como el puente intelectual definitivo. Es la disciplina que nos permite pasar de lo que vemos —una pequeña muestra— a la realidad oculta de la población total. En esencia, es la herramienta científica que transforma la observación de unos pocos en el conocimiento preciso de la mayoría.

Población frente a muestra: la ventana hacia la verdad

Para descifrar la realidad, primero debemos distinguir entre los dos protagonistas del análisis: la población y la muestra. La población es el conjunto total que deseamos estudiar y la muestra es un subconjunto extraído de forma aleatoria que nos sirve de ventana para observar la población.

En este proceso, manejamos conceptos que debemos diferenciar con rigor:

  • Parámetro: Es el número «secreto» que describe la población. En la práctica, su valor es desconocido porque no podemos examinar a cada individuo. Usamos símbolos como la media poblacional (μ), la desviación típica (σ), la varianza (σ²) o el porcentaje o la proporción poblacional (p).
  • Estadístico: Es el número que calculamos directamente a partir de los datos muestrales. En este ámbito operamos con la media muestral, la desviación típica muestral, la varianza o la proporción muestral.

Dado que no podemos conocer el parámetro real, nos vemos obligados a operar en el mundo de los estadísticos para realizar estimaciones. El objetivo es claro:

«Extraer conclusiones sobre una población a partir de los datos de una muestra».

El intervalo de confianza: ¿qué tan cerca estamos de la realidad?

Dado que trabajar con muestras implica un error aleatorio inevitable, la estadística no ofrece un único número como verdad absoluta. En su lugar, construimos un intervalo de confianza de nivel C.

Conceptualmente, este rango se define mediante una estructura lógica: estimación ± error de la estimación.

No proporcionamos un único valor porque, en la práctica, el parámetro no se conoce. Por ello, el nivel de confianza C no es solo un porcentaje, sino la respuesta a una pregunta vital sobre la fiabilidad de nuestro trabajo: «¿Con qué frecuencia daría una respuesta correcta este método si lo utilizara muchas veces?». Si afirmamos que tenemos un 95 % de confianza, estamos diciendo que, si repitiéramos el muestreo el 95 % de las veces, nuestro intervalo contendría el verdadero valor del parámetro.

Inocente hasta que se demuestre lo contrario: la hipótesis nula (H0)

Como expertos, empleamos el contraste de hipótesis para evaluar si la evidencia de la muestra es suficiente para inferir una condición en toda la población. Este mecanismo examina dos afirmaciones opuestas:

La hipótesis nula (H0) representa el estado «habitual» o lo que cabría esperar si no hubiera cambios. Es una afirmación de «ausencia de efecto» o de «no diferencia». Algunos ejemplos críticos de H₀ son:

  • El acusado no es culpable (es inocente).
  • No hay embarazo.
  • No hay presencia de cáncer.

Para decidir si rechazamos la hipótesis nula, calculamos el p-valor (o significación muestral). A diferencia de lo que se cree popularmente, el p-valor no es un corte arbitrario, sino la probabilidad de obtener nuestros resultados si la hipótesis nula fuera cierta. Comparamos este p-valor con el nivel de significación (α), que es el límite preestablecido. Si p ≤ α, la evidencia es tan fuerte que rechazamos la situación «habitual» en favor de la hipótesis alternativa.

El dilema del error: falsos positivos y falsos negativos

En cualquier prueba estadística, asumimos el riesgo de tomar una decisión equivocada. Estos errores se dividen en dos categorías fundamentales:

  • Error tipo I (α): el «falso positivo» o riesgo del fabricante. Ocurre cuando rechazamos la hipótesis nula cuando esta es verdadera (por ejemplo, operar a una persona sana o condenar a un inocente).
  • Error tipo II (β): el «falso negativo». Sucede cuando aceptamos la hipótesis nula cuando es falsa (por ejemplo, declarar inocente a un asesino o no detectar una enfermedad).

Para minimizar estos riesgos, no solo tenemos en cuenta el nivel de significación (típicamente fijado en el 5 %), sino que también buscamos maximizar la potencia de la prueba (1 – β). Esta potencia representa nuestra capacidad para detectar un efecto cuando realmente existe y depende directamente del tamaño de la muestra y del nivel de significación. Decimos que un resultado tiene significación estadística cuando es tan improbable que no puede atribuirse razonablemente al azar (p ≤ α).

Propiedades del buen estimador

Para que nuestras conclusiones sean robustas, los métodos que utilizamos deben poseer cuatro pilares técnicos extraídos de la teoría de la probabilidad:

  • Sesgo: el estimador debe carecer de desviaciones sistemáticas; su media debe coincidir con el parámetro real.
  • Eficiencia: buscamos la menor variabilidad posible en los resultados.
  • Convergencia y consistencia: estas propiedades garantizan la fiabilidad del método a largo plazo.

La lógica matemática que hay detrás de la eficiencia es poderosa: si aumenta el tamaño de la muestra, disminuye la varianza del estimador. Esta es la razón técnica por la que una encuesta con miles de personas es más «eficiente» y nos acerca más a la verdad que una consulta informal: al reducir la varianza, estrechamos el margen de error y ganamos precisión.

Conclusión: una mirada al futuro de las decisiones

La inferencia estadística es la ciencia que se ocupa de gestionar la incertidumbre para alcanzar la precisión. Nos enseña que, si bien es imposible tener certeza absoluta sobre una población masiva, el rigor matemático nos permite actuar con una seguridad asombrosa.

Aceptar que nuestras conclusiones conviven con un nivel de confianza y un riesgo de error no debilita el conocimiento, sino que lo fortalece al hacerlo verificable y científico. La próxima vez que lea el titular de una encuesta electoral o el estudio de un nuevo tratamiento, no se quede en la superficie. Pregúntese: ¿cuál es el margen de error?, ¿es el p-valor realmente significativo? Si posee estas cinco claves, pasará de ser un consumidor pasivo de datos a ser un pensador crítico capaz de ver lo invisible.

En esta conversación puedes escuchar las ideas más interesantes sobre inferencia estadística.

El vídeo resume bien los conceptos más importantes de este tema.

Licencia de Creative Commons
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

¿Por qué nada en la ciencia es exacto? Cómo entender y calcular el error experimental

Jorge Luis Borges imaginó una vez un imperio en el que el arte de la cartografía alcanzó tal perfección que el mapa de una sola provincia ocupaba toda una ciudad. Finalmente, los cartógrafos trazaron un mapa del imperio que tenía el mismo tamaño que este y coincidía punto por punto con él. Por supuesto, aquel mapa era inútil.

En ciencia sucede algo similar: medir no es replicar la realidad, sino crear un mapa de ella. Estamos obsesionados con la exactitud, pero en el laboratorio pronto aprendemos que la «medida exacta» es una quimera. Medir no consiste en capturar una verdad absoluta, sino en gestionar con elegancia la incertidumbre. Un dato sin su margen de error no es una medida, sino una simple expresión de deseos.

1. La ilusión de la exactitud: el error es inevitable.

En metrología, la humildad es una competencia técnica. Debemos aceptar que nuestros sentidos y nuestros instrumentos están limitados por definición. La teoría de los errores nos enseña que el «valor verdadero» es un ideal matemático al que solo podemos aproximarnos. El error no es una equivocación del científico, sino una propiedad inherente al acto de medir.

Existen dos fuerzas que distorsionan nuestro «mapa» de la realidad:

  • El error sistemático es un sesgo constante. Aparece cuando la metodología es inadecuada, los instrumentos están mal calibrados o los patrones de medición son dudosos. Se trata de un error predecible que desplaza todas nuestras mediciones en la misma dirección, alejándolas de la realidad.
  • El error accidental o aleatorio es el «ruido» del universo. Se debe al azar, a variaciones microscópicas y a factores incontrolables. Se manifiestan como pequeñas fluctuaciones al repetir una medición y, aunque no pueden eliminarse, la estadística es nuestra herramienta para controlarlas.

Para navegar por esta complejidad, distinguimos entre exactitud (cuán cerca está nuestra flecha del centro de la diana) y precisión (cuán cerca están las flechas entre sí, independientemente de dónde hayan caído).

«El error se define como la diferencia entre el valor verdadero y el obtenido experimentalmente».

2. El drama de los ceros: el límite de nuestro conocimiento.

En el lenguaje técnico, los números no solo indican cantidades, sino que también expresan confianza. No es lo mismo informar de un peso de «1,5 g» que de uno de «1,500 g». Las cifras significativas son los dígitos que realmente aportan información sobre la precisión de nuestra medición.

Para entenderlas, seguimos unas reglas claras:

  • Cualquier dígito distinto de cero es significativo.
  • Los ceros situados entre dígitos significativos (por ejemplo, 2,054) siempre cuentan.
  • Los ceros a la izquierda (por ejemplo, 0,076) son solo marcadores de posición decimal.
  • Los ceros situados a la derecha del punto decimal (por ejemplo, 0,0540) son fundamentales, ya que indican que el instrumento fue capaz de medir esa posición.

El número «1500» es el ejemplo clásico de ambigüedad: ¿es una aproximación a la centena o una medida exacta en gramos? La notación científica resuelve el misterio: 1,5 × 10^(3) indica dos cifras significativas, mientras que 1,500 × 10^(3) indica cuatro. Aquí reside una reflexión profunda: la última cifra significativa siempre es incierta. Es el límite de nuestra visión, el punto en el que nuestra capacidad de observación se desvanece en la duda.

3. La paradoja de la resta: el «caso más desfavorable».

Uno de los conceptos más fascinantes y contraintuitivos es la propagación de errores. Imaginemos que pesamos una tetera colocando pesas en un platillo. Si la masa de la tetera se obtiene restando la masa del plato de la masa total, podrías pensar que los errores también se restan. Sin embargo, la ciencia es conservadora por necesidad.

En metrología, trabajamos bajo la filosofía del caso más desfavorable. Si la medida A presenta un error por exceso y la medida B, por defecto, al restarlas (A – B) el error total resultante no disminuye, sino que aumenta. Las incertidumbres nunca se anulan; siempre se acumulan.

  • En sumas y restas, las cotas de error absoluto se suman.
  • En multiplicaciones y divisiones, lo que sumamos son los errores relativos.

Cuando multiplicamos, no solo añadimos «milímetros» de duda, sino que también multiplicamos la incertidumbre de la proporción misma, lo que amplía el margen de error de nuestro mapa original.

4. La regla de oro: la estética del rigor.

La honestidad metrológica tiene una regla estética: el error absoluto generalmente se expresa con una sola cifra significativa. No tiene sentido decir que una montaña mide 2000,432 metros, con un error de 12,45 metros. La duda en las decenas anula cualquier certeza en los milímetros.

Sin embargo, existen dos excepciones en las que se permiten dos cifras significativas en el error:

  • Si la primera cifra es un 1.
  • Si la primera cifra es un 2 seguido de una cifra menor que 5 (es decir, hasta 24).

La regla del redondeo es estricta: se redondea por exceso en una unidad si la segunda cifra es 5 o superior. Finalmente, el valor y su error deben tener el mismo número de decimales.

Corrección de estilo metrológico

5. El criterio de dispersión: ¿cuándo es suficiente?

¿Cuántas mediciones necesitamos para que nuestra media sea fiable? Si solo realizamos una medición, el error dependerá directamente del instrumento.

  • En los instrumentos digitales, el error se expresa como la sensibilidad (S).
  • En los instrumentos analógicos, el error es la mitad de la sensibilidad (S/2).

Pero cuando la precisión es crítica, recurrimos a la estadística. A continuación, comento un criterio usado en algunas publicaciones, como la de Fernando Senent, aunque también se pueden consultar otros criterios en este otro documento. En cualquier caso, el proceso siempre comienza con 3 medidas iniciales para calcular el criterio de dispersión (T):

Para series largas (N ≥ 15), utilizamos el error cuadrático medio (ECM). Este cálculo parte de la suposición de que nuestros datos siguen una distribución gaussiana (la famosa campana de Gauss), según la cual el 68,3 % de las medidas se encontrarán dentro de un margen de error cuadrático medio respecto a la media. Es el reconocimiento matemático de que el azar tiene una estructura.

Conclusión: la honestidad de la incertidumbre.

La ciencia no es el dominio de las verdades absolutas, sino el territorio de la incertidumbre controlada. Aceptar el error, nombrarlo y calcularlo no es una debilidad, sino la máxima expresión de la integridad técnica. Al acotar lo que no sabemos, protegemos la validez de lo que sí sabemos.

¿Cómo cambiaría nuestra percepción del mundo si aceptáramos que cada «dato real» que consumimos, desde las estadísticas económicas hasta los resultados de un análisis clínico, viene acompañado de un margen de error invisible? Quizás dejaríamos de buscar certezas absolutas y empezaríamos a valorar la honestidad de la duda bien calculada.

En esta conversación puedes escuchar las ideas más interesantes de este artículo.

Aquí tienes un resumen en formato de vídeo sobre los aspectos clave de la medición.

Por último, creo que este resumen puede resultar de interés.

Medición_y_error_La_guía_maestra

Licencia de Creative Commons
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

¿Quieres más datos? No siempre es mejor: la lección que cambiará tu forma de ver la ciencia.

En la era del Big Data, tenemos, casi instintivamente, la idea de que más información siempre es mejor. Acumular más datos parece el camino directo hacia decisiones más inteligentes, resultados más fiables y una certeza casi absoluta. Creemos que si medimos algo diez, cien o mil veces, nuestra comprensión del fenómeno será inevitablemente más profunda y precisa.

Sin embargo, en el ámbito de la experimentación científica rigurosa, esta intuición puede resultar peligrosamente engañosa. Existe un concepto fundamental que a menudo se pasa por alto y que es mucho más importante que la mera cantidad de mediciones. No se trata de cuántos datos se recogen, sino de cómo se recogen. La estructura de un experimento es clave para su eficacia.

En este artículo se desglosan tres ideas clave del diseño experimental que revelan por qué la arquitectura de un estudio es más relevante que la cantidad de datos brutos. Prepárate para descubrir el secreto del éxito en los experimentos.

1. ¿Quién es nuestro protagonista? La unidad experimental.

Todo experimento comparativo tiene una estrella principal, un elemento central en torno al cual gira toda la acción. No se trata del tratamiento aplicado ni de la variable medida, sino de la unidad experimental (UE). Pero, ¿qué es exactamente?

Una unidad experimental es el elemento más pequeño al que se puede asignar un tratamiento de forma completamente independiente. Es la pieza fundamental sobre la que se realizan las mediciones para determinar qué ocurre. Piensa en ella como el «sujeto» de tu experimento.

Los ejemplos concretos ayudan a entenderlo mejor:

  • En la agricultura, si quieres comparar dos tipos de fertilizantes, la unidad experimental podría ser una parcela de terreno de un tamaño determinado.
  • En un estudio médico, la unidad experimental suele ser un paciente.
  • En entomología, podría tratarse de un insecto concreto o incluso de una colonia entera.

La clave está en que la definición de la unidad experimental depende de los objetivos de la investigación. Se trata de la pieza fundamental sobre la que se construye toda la comparación. Definir esta unidad es el primer paso, pero el verdadero desafío surge cuando empezamos a tomar mediciones en ella, lo que nos lleva a una de las trampas más comunes de la ciencia.

2. El espejismo de los «diez datos»: por qué medir más no siempre es medir mejor.

Esta es una de las confusiones más frecuentes. A menudo, en una unidad experimental podemos tomar varias mediciones. A estos subelementos los llamamos «unidades muestrales». Por ejemplo, en una parcela de terreno (la UE) podríamos analizar diez plantas distintas (las unidades muestrales).

Parecería que tenemos diez datos, ¿verdad? Técnicamente, sí, pero no son lo que parecen. Hay una regla de oro en el diseño experimental que lo cambia todo:

Las unidades muestrales dentro de una misma unidad experimental deben recibir el mismo tratamiento. Por ello, la asignación del tratamiento a estas unidades muestrales no es independiente entre sí.

Esto tiene unas implicaciones enormes. Las diez plantas de la misma parcela son como hermanos que crecieron en la misma casa. Comparten el mismo terreno, la misma cantidad de luz solar y la misma cantidad de agua. Medirlas por separado no es lo mismo que entrevistar a diez personas de distintas partes de la ciudad. Su similitud y su falta de independencia significan que no se obtienen diez puntos de vista únicos, sino diez variaciones sobre el mismo punto de vista. Confundir estas muestras con diez unidades experimentales independientes es uno de los errores más frecuentes al interpretar resultados.

Entonces, si multiplicar las muestras en una misma parcela no aumenta la fiabilidad, ¿cómo podemos estar seguros de que nuestro tratamiento funciona? La respuesta no consiste en acumular más mediciones, sino en comprender y medir correctamente el «ruido» del sistema.

3. Abraza el ruido: por qué el «error experimental» es tu mejor aliado.

La palabra «error» tiene una connotación negativa, pero en la ciencia el error experimental es tu mejor aliado. No se refiere a una equivocación ni a un fallo de medición. Se trata simplemente de la variabilidad natural entre las unidades experimentales. Es el «ruido» de fondo inevitable del sistema que estás estudiando. Dos pacientes nunca son idénticos ni dos parcelas de terreno son clones perfectos.

Para medir este «ruido» natural, necesitamos comparar manzanas con manzanas. Por eso la unidad experimental (Idea 1) es tan importante. La pequeña variación entre diez plantas de la misma parcela (las unidades muestrales de la idea 2) no nos dice nada sobre la variabilidad natural entre parcelas. El verdadero error experimental solo puede medirse comparando las diferencias entre múltiples parcelas completas que recibieron el mismo tratamiento.

La diferencia de altura entre dos plantas situadas a pocos centímetros entre sí en la misma parcela bien fertilizada será mínima. Esta pequeña variación no nos dice nada sobre la eficacia del fertilizante en general, especialmente si lo comparamos con otra parcela que, por su composición natural, presenta un suelo completamente diferente. La variación entre las parcelas es lo que constituye el verdadero desafío. La esencia de un buen experimento consiste en determinar si el efecto del tratamiento es mayor que la variabilidad natural. Sin una medición honesta de este error, es imposible sacar conclusiones válidas.

Conclusión: mirar más allá de los números.

La validez de un experimento no depende de la cantidad de mediciones, sino de la correcta definición, asignación y comparación de sus unidades experimentales. Es la estructura, no el volumen, lo que permite separar la señal del ruido.

La próxima vez que leas sobre un nuevo estudio, ignora por un momento el deslumbrante número de mediciones. En su lugar, busca a la verdadera protagonista: la unidad experimental. Pregúntate cómo la definieron los investigadores y cómo la utilizaron para medir el ruido de fondo. Esa es la diferencia entre una montaña de datos y un verdadero descubrimiento.

En esta conversación puedes descubrir alguna de las ideas de este artículo.

También puedes ver este vídeo, donde se recogen los conceptos más interesantes del tema.

Licencia de Creative Commons
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Unidades experimentales y muestrales en el diseño de experimentos

La unidad experimental (UE) es el elemento central en el diseño y el análisis de experimentos comparativos. Se define como la entidad a la que se le puede asignar un tratamiento de forma independiente y sobre la cual se realizan las mediciones. La identificación correcta de la UE es fundamental, ya que la estimación de la variabilidad natural, conocida como error experimental, depende exclusivamente de la comparación entre unidades experimentales idénticas que reciben el mismo tratamiento.

Una unidad experimental puede contener múltiples unidades muestrales, subelementos que reciben obligatoriamente el mismo tratamiento que la UE a la que pertenecen. Por esta razón, la variabilidad entre estas unidades muestrales internas no resulta útil para estimar el efecto del tratamiento. Un diseño experimental sólido se basa en la capacidad de distinguir los efectos reales de los tratamientos del «ruido» natural del sistema, una distinción que solo es posible mediante la correcta cuantificación de la variabilidad entre las unidades experimentales completas.

Definiciones fundamentales

El marco de un experimento se define a través de sus componentes básicos, en los que la unidad experimental y la unidad muestral desempeñan funciones distintas, aunque interconectadas.

1. La unidad experimental (UE)

La unidad experimental es el pilar de cualquier ensayo comparativo. Su definición formal es la siguiente:

«El elemento sobre el que se realizan las mediciones y al que se puede asignar un tratamiento de forma independiente».

El conjunto de todas las unidades experimentales disponibles para un estudio se denomina material experimental. La definición de una UE es flexible y se adapta a los objetivos de la investigación.

Ejemplos prácticos:

  • Ensayo de resistencia del hormigón: la unidad experimental puede ser un bloque o un cilindro de hormigón elaborado con una mezcla específica. Las unidades muestrales serían las probetas o las muestras extraídas del mismo bloque para realizar ensayos de compresión o de flexión.
  • Prueba de rendimiento de pavimentos: la unidad experimental puede ser un tramo de vía construido con un diseño o material específico (por ejemplo, un segmento de 50 metros). Las unidades muestrales serían los puntos de medición dentro del tramo, por ejemplo, las deflexiones o la rugosidad.
  • Ensayo de estructuras a escala en laboratorio: la unidad experimental puede ser una viga o una columna, construida según un diseño específico. Las unidades muestrales serían los puntos de medición (deformaciones, desplazamientos o tensiones) registrados por sensores a lo largo de la estructura.

El criterio esencial para definir una UE es que sea capaz de recibir diferentes tratamientos de manera independiente de las demás unidades.

2. La unidad muestral.

Dentro de una unidad experimental pueden existir subelementos en los que se aplican las condiciones experimentales. A estos se les conoce como unidades muestrales.

La regla fundamental que las rige es que todas las unidades muestrales de una misma unidad experimental deben recibir el mismo tratamiento. Como consecuencia directa, la asignación del tratamiento a estas subunidades no es independiente entre sí, lo que tiene implicaciones críticas para el análisis estadístico.

El papel de la estimación en la variabilidad.

La distinción entre unidades experimentales y muestrales es crucial para inferir correctamente los efectos de un tratamiento, ya que incide directamente en la medición de la variabilidad del sistema.

a. El error experimental

Para evaluar si un tratamiento tiene un efecto real, es necesario conocer la variabilidad natural del material experimental. Esta variabilidad inherente se conoce como error experimental. Es la base contra la que se comparan las diferencias observadas entre los tratamientos.

b. Metodología de estimación

La estimación correcta del error experimental solo se logra a partir de las diferencias observadas entre unidades experimentales que, en principio, son idénticas y han recibido el mismo tratamiento.

  • Fuente de estimación válida: la variación entre unidades experimentales es la única que permite estimar correctamente el error experimental.
  • Fuente de estimación no válida: la variación entre las unidades muestrales dentro de una misma unidad experimental es, por lo general, muy pequeña y no proporciona información útil para estimar el efecto del tratamiento ni el error experimental.

La observación clave es que «solo la unidad experimental completa permite estimar correctamente el error experimental».

Tipología de variables en un experimento.

Los datos recopilados en un experimento se organizan en dos categorías principales de variables:

Tipo de variable Descripción
Variables de respuesta Son las mediciones obtenidas de las unidades experimentales. Sus valores reflejan tanto los efectos de los tratamientos como la variabilidad natural del sistema.
Variables explicativas (factores) Son las variables que se manipulan o controlan porque se cree que influyen en las variables de respuesta. Incluyen los factores de clasificación, que definen los niveles o categorías sobre los cuales se realizan las inferencias estadísticas.

Conclusión: el fundamento de un diseño sólido.

La estructura de un diseño experimental robusto se basa en comparar unidades experimentales similares. Este enfoque permite a los investigadores distinguir de manera fiable el efecto real de los tratamientos aplicados del «ruido» o de la variabilidad natural inherente al sistema experimental. Por tanto, la identificación precisa y la gestión adecuada de la unidad experimental no son meros detalles técnicos, sino requisitos indispensables para que las conclusiones científicas derivadas del experimento sean válidas y fiables.

En este documento tenéis un resumen de las ideas más importantes.

Pincha aquí para descargar

Licencia de Creative Commons
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Pánico, secreto y vientos diagonales: La crisis de 59 pisos que casi colapsa el Citigroup Center

Base del Citigroup Center junto a la Iglesia de San Pedro, lo que obligó a una disposición inusual de las columnas. https://es.wikipedia.org/wiki/Citigroup_Center

Introducción: El gigante con pies de barro.

Los rascacielos son monumentos a la permanencia. Se elevan sobre nuestras ciudades como símbolos de ingenio, poder y estabilidad estructural. Sin embargo, en 1978, el Citigroup Center, uno de los edificios más innovadores y reconocibles de Nueva York, ocultaba un secreto aterrador. Inaugurado con gran fanfarria en 1977, este hito de la ingeniería estaba, de hecho, peligrosamente cerca del colapso.

La ironía central de esta historia es casi cinematográfica: el fallo catastrófico se descubrió gracias a la pregunta de una estudiante universitaria, y la persona que cometió el error de cálculo que puso en peligro a miles de personas fue la misma que se convirtió en el héroe que los salvó. Esta es la historia de cómo una combinación de error humano, ética profesional y una suerte increíble evitó uno de los mayores desastres arquitectónicos de la historia moderna.

1. No bastó con un solo error; se necesitaron dos para poner en jaque al gigante.

El fallo que puso en jaque al Citigroup Center no fue un simple descuido, sino la combinación de dos errores críticos que se multiplicaron entre sí.

El primero fue un error de cálculo cometido por William LeMessurier, el ingeniero jefe. Siguiendo el código de construcción de la época, calculó las cargas de viento que incidían perpendicularmente en las caras del edificio. Sin embargo, debido al diseño único de la torre, que estaba apoyada sobre cuatro enormes pilares situados en el centro de cada lado en lugar de en las esquinas, pasó por alto que los vientos diagonales (conocidos como quartering winds) ejercían una tensión mucho mayor. Este descuido incrementó la carga en las uniones estructurales clave en un 40 %.

El segundo error agravó fatalmente el primero. Durante la construcción, la empresa constructora Bethlehem Steel propuso sustituir las uniones soldadas, que eran más resistentes pero también más costosas, por uniones atornilladas, más económicas. Basándose en los cálculos originales de vientos perpendiculares, este cambio parecía una modificación rutinaria y segura, por lo que la oficina de LeMessurier lo aprobó sin que él revisara personalmente las implicaciones. En aquel momento, fue una decisión técnicamente sólida, pero con el paso del tiempo se consideró fatal.

La combinación de un error oculto y una decisión que parecía segura resultó devastadora. La carga adicional del 40 % de los vientos diagonales aplicada a las uniones atornilladas más débiles provocó un aumento catastrófico del 160 % en la tensión de las conexiones. Esto significaba que una tormenta que ocurre cada 55 años podría ser desastrosa. Sin embargo, el peligro real era aún mayor: si el amortiguador de masa sintonizado del edificio, que dependía de la electricidad, fallaba durante un apagón —algo muy probable durante un huracán—, una tormenta mucho más común, de las que golpean Nueva York cada dieciséis años, podría derribarlo.

2. El «héroe» de la historia fue el ingeniero que cometió el error.

Tras descubrir el fallo, William LeMessurier se enfrentó a un dilema ético devastador. Años después, relataría que consideró todas las opciones, desde guardar silencio y arriesgar miles de vidas hasta el suicidio para escapar de la desgracia profesional.

Sin embargo, LeMessurier tomó la decisión más honorable: asumir toda la responsabilidad. Consciente de que esto podría significar el fin de su carrera, la bancarrota y la humillación pública, se puso en contacto con los directivos de Citicorp para informarles de que su flamante rascacielos de 175 millones de dólares era fundamentalmente inseguro. En ese momento, su mentalidad no se limitaba al deber, sino que también reflejaba un profundo sentido de su posición única, como él mismo describió:

«Tenía información que nadie más en el mundo poseía. Tenía en mis manos el poder de influir en eventos extraordinarios que solo yo podía iniciar».

Para su sorpresa, la reacción de los ejecutivos de Citicorp, liderados por el presidente Walter Wriston, no fue de ira, sino de una calma pragmática. En lugar de buscar culpables, Wriston se centró de inmediato en la solución. Pidió un bloc de notas amarillo, empezó a redactar un comunicado de prensa y bromeó: «Todas las guerras se ganan con generales que escriben en blocs amarillos». Este gesto de liderazgo, enfocado y sereno, sentó las bases para la increíble operación de rescate que estaba a punto de comenzar.

El Citigoup Center. https://es.wikipedia.org/wiki/Citigroup_Center

3. Una llamada casual de una estudiante lo desencadenó todo.

Toda esta crisis existencial y de ingeniería se desencadenó en junio de 1978 por un hecho tan improbable como una simple llamada telefónica. Al otro lado de la línea estaba Diane Hartley, una estudiante de ingeniería de la Universidad de Princeton que analizaba la estructura del Citigroup Center para su tesis.

Hartley llamó a LeMessurier con preguntas sobre la estabilidad del edificio frente a vientos diagonales. Confiado en su diseño, LeMessurier le explicó pacientemente por qué la estructura era sólida. Sin embargo, la llamada de Hartley sembró una semilla. No porque tuviera una preocupación inmediata, sino porque la conversación lo inspiró, LeMessurier decidió que el tema sería un excelente ejercicio académico para la conferencia que preparaba para sus propios estudiantes de Harvard.

Fue durante este recálculo, realizado por pura curiosidad intelectual, cuando descubrió con horror su error original. La llamada casual de Hartley no le dio la respuesta, pero le hizo la pregunta correcta en el momento adecuado, lo que supuso el golpe de suerte que reveló una vulnerabilidad mortal y activó la carrera contrarreloj para evitar una catástrofe inimaginable.

4. Una operación secreta, un huracán y una huelga de prensa lo mantuvieron en secreto.

La reparación del Citigroup Center fue una operación clandestina de alta tensión. Bajo el nombre en clave «Proyecto SERENE», los equipos trabajaban con una precisión coreografiada. Cada noche, los carpinteros llegaban a las 17:00 h para construir recintos de madera contrachapada alrededor de las juntas que había que reparar. Entre las 20:00 y las 04:00, con el sistema de alarma contra incendios desactivado, los soldadores trabajaban para reforzar más de doscientas uniones atornilladas con placas de acero de dos pulgadas de espesor. Finalmente, un equipo de limpieza eliminaba todo rastro del trabajo antes de la llegada de los primeros empleados a las 8 a. m., ajenos al peligro que se cernía sobre ellos.

El drama alcanzó su punto álgido a principios de septiembre de 1978, cuando el huracán Ella, una tormenta muy intensa, se dirigía directamente hacia la ciudad de Nueva York. Con las reparaciones a medio terminar, el edificio seguía siendo vulnerable. En secreto, las autoridades elaboraron planes para evacuar la torre y una zona de diez manzanas a su alrededor.

Entonces, la suerte intervino de nuevo. A pocas horas de la posible catástrofe, el huracán Ella viró inesperadamente hacia el Atlántico, salvando a la ciudad. El suspiro de alivio fue inmenso. Y, como si esto no fuera suficiente, un último golpe de fortuna mantuvo todo en secreto: justo cuando la historia estaba a punto de filtrarse, comenzó una huelga de periódicos en toda la ciudad que duró varios meses. La huelga enterró la noticia por completo y el casi desastre permaneció oculto al público durante casi veinte años, hasta que fue revelado en un artículo de The New Yorker en 1995.

Conclusión: la delgada línea entre el desastre y la ética.

La historia del Citigroup Center es un poderoso recordatorio de la fragilidad que puede esconderse tras una apariencia de fortaleza. Una combinación de error humano, profunda ética profesional, liderazgo decisivo y una buena dosis de suerte evitó lo que podría haber sido uno de los peores desastres arquitectónicos de la historia. El ingeniero que cometió el error lo afrontó con una valentía que salvó incontables vidas y, paradójicamente, reforzó su reputación.

La historia del Citigroup Center nos recuerda que incluso los símbolos de la permanencia pueden ser frágiles. Nos deja con una pregunta: ¿cuántos otros secretos se esconden en las estructuras que nos rodean, esperando a que una simple pregunta los saque a la luz?

En esta conversación puedes escuchar las ideas más interesantes sobre este asunto.

Aquí puedes ver un vídeo que resume bien el contenido del artículo.

 

Licencia de Creative Commons
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Clasificación y principios fundamentales del diseño experimental

Cuando pensamos en un experimento, solemos imaginar una prueba simple para ver qué opción es “mejor”. Sin embargo, esta visión apenas roza la superficie de una disciplina profunda y estratégica. Existen principios sorprendentes que rigen el diseño experimental y son cruciales no solo para la ciencia, sino también para cualquier toma de decisiones informada. A continuación, se describen brevemente los tipos de experimentos que pueden utilizarse en la investigación científica.

El diseño experimental se clasifica en dos categorías principales, según la propuesta de Anscombe (1947): el experimento absoluto y el experimento comparativo. El experimento absoluto se enfoca en la medición de propiedades físicas constantes para ampliar el conocimiento científico, utilizando un modelo estadístico de efectos aleatorios (Modelo II de Eisenhart), ya que los tratamientos se seleccionan al azar de una población más amplia. Por el contrario, el experimento comparativo está orientado a la toma de decisiones en ciencias aplicadas, con el fin de determinar cuál de varios tratamientos predefinidos es “mejor”. Este enfoque utiliza un modelo de efectos fijos (Modelo I de Eisenhart) y exige una definición precisa del problema para garantizar su validez.

El éxito de un experimento, especialmente el comparativo, depende del cumplimiento de cinco principios fundamentales: simplicidad, nivel de precisión adecuado, ausencia de error sistemático, amplio rango de validez de las conclusiones y una correcta cuantificación de la incertidumbre. La elección del diseño y el modelo estadístico asociado (fijo, aleatorio o mixto) determinan directamente el alcance y la naturaleza de las inferencias que pueden extraerse, vinculando de manera inseparable la planificación experimental con las conclusiones científicas y las decisiones de gestión.

La clasificación propuesta por Anscombe distingue los experimentos en dos grandes tipos según su objetivo fundamental: la adquisición de conocimiento puro o la fundamentación de decisiones prácticas.

Uno de ellos es el llamado experimento absoluto. En este tipo de experimento, el interés principal es medir y conocer las propiedades físicas de una población. Se asume que dichas propiedades permanecen constantes, lo que justifica el uso del término absoluto. El objetivo no es comparar alternativas concretas, sino ampliar el conocimiento científico sobre el fenómeno estudiado.

Los experimentos absolutos suelen centrarse en un solo factor y consideran un número limitado de tratamientos o niveles de ese factor. Estos tratamientos suelen elegirse de forma aleatoria. Por esta razón, si el experimento se repite, no es obligatorio utilizar exactamente los mismos tratamientos en cada ocasión.

Debido a esta forma de selección, los tratamientos se consideran variables aleatorias. En consecuencia, el análisis se basa en un modelo de efectos aleatorios, también conocido como el Modelo II de Eisenhart (1947). Este tipo de modelo permite identificar y estimar los distintos componentes de la variación aleatoria presentes en una población compuesta, lo que constituye un enfoque especialmente útil para muchos problemas de ingeniería.

El experimento comparativo es el segundo tipo de experimento descrito por Anscombe. Este enfoque se utiliza cuando se analizan varios tratamientos y se observa que, aunque los valores absolutos de los resultados pueden fluctuar de forma irregular, las comparaciones relativas entre tratamientos suelen mantenerse estables. En este contexto, es posible concluir que, bajo condiciones similares, algunos tratamientos ofrecen resultados claramente mejores que otros.

Brownlee (1957) sitúa este tipo de experimentos en el ámbito de las ciencias aplicadas, y no es casualidad: la teoría estadística del diseño de experimentos se desarrolló originalmente para responder a las necesidades de este tipo de estudios.

En un experimento comparativo, los tratamientos se evalúan según su efecto promedio sobre una variable de respuesta, con el objetivo principal de determinar cuál es “mejor” según un criterio definido. A diferencia de los experimentos orientados al conocimiento fundamental, aquí el propósito central es apoyar la toma de decisiones prácticas, especialmente las administrativas o de gestión.

Una característica fundamental de los experimentos comparativos es que todos los tratamientos de interés están incluidos explícitamente en el estudio. Por esta razón, el análisis se basa en un modelo de efectos fijos, también conocido como el Modelo I de Eisenhart (1947). Si el experimento se repite, se utilizan exactamente los mismos tratamientos, ya que no se considera una muestra aleatoria. El interés principal radica en detectar y estimar relaciones constantes entre las medias de los tratamientos, lo que conduce naturalmente a la evaluación de hipótesis estadísticas sobre dichas medias.

Para que un experimento comparativo sea válido, debe comenzar con una definición clara y precisa del problema. No basta con plantear de manera general la idea de “comparar tratamientos”. Es imprescindible especificar con detalle los objetivos del estudio y formular con precisión las hipótesis que se probarán. Esta definición inicial determina la población a la que se aplicarán las conclusiones, identifica los factores, los tratamientos y sus niveles, establece las variables de respuesta que se medirán y define qué diferencias entre tratamientos se consideran relevantes. Sin estas especificaciones, no es posible diseñar un experimento adecuado.

Finalmente, una consecuencia natural de los experimentos comparativos es que casi siempre conducen a decisiones concretas. Dado un nivel suficiente de recursos, la hipótesis nula de igualdad entre tratamientos puede rechazarse, lo que obliga a actuar: mantener la situación actual o cambiar a un nuevo tratamiento. Este proceso de decisión consta de dos etapas bien definidas:

  1. Análisis estadístico de los datos, en el que se evalúan las probabilidades asociadas a los resultados y se extraen conclusiones técnicas.
  2. Decisión de gestión en la que, con base en esas conclusiones, se define la acción a realizar.

Esta conexión directa entre el análisis estadístico y la toma de decisiones explica por qué los experimentos comparativos son una herramienta central en la divulgación y la práctica de la ingeniería y de las ciencias aplicadas.

El estadístico cumple un rol clave en el proceso experimental: su responsabilidad es presentar, con la mayor precisión posible, las probabilidades obtenidas en la etapa de análisis, de manera que se reduzca al mínimo la posibilidad de tomar decisiones equivocadas cuando llegue el momento de actuar.

Dado que las decisiones sobre las hipótesis dependen directamente de experimentos cuidadosamente planificados, es esencial que dichos ensayos cumplan con una serie de principios básicos. A continuación se resumen los más importantes, con un enfoque práctico para la ingeniería:

  • Simplicidad: Tanto la selección de los tratamientos como la organización del experimento deben ser lo más simples posible. Un diseño sencillo facilita el análisis estadístico y la interpretación de los resultados y reduce el riesgo de errores innecesarios.
  • Nivel de precisión: El experimento debe permitir detectar diferencias entre tratamientos con el grado de precisión que el investigador considere relevante. Para lograrlo, se requiere un diseño experimental adecuado y un número suficiente de repeticiones que garanticen mediciones confiables.
  • Ausencia de error sistemático: El experimento debe planearse de modo que las unidades experimentales que reciben distintos tratamientos no difieran sistemáticamente entre sí antes de aplicarlos. Este cuidado es fundamental para obtener estimaciones insesgadas del efecto real de cada tratamiento, evitando que factores externos distorsionen los resultados.
  • Rango de validez de las conclusiones: Las conclusiones del experimento deben ser aplicables a un rango de situaciones lo más amplio posible. Los experimentos replicados y los diseños factoriales ayudan a ampliar este rango de validez, ya que permiten evaluar la consistencia de los resultados bajo diferentes condiciones.
  • Cuantificación de la incertidumbre: Todo experimento conlleva cierto grado de incertidumbre. Por ello, el diseño debe permitir calcular la probabilidad de que los resultados observados se deban únicamente al azar. Esta cuantificación es esencial para evaluar la solidez de las conclusiones.

Estos principios conducen a una clasificación clásica de los modelos estadísticos, propuesta por Eisenhart (1947), que conecta el diseño del experimento con el tipo de inferencia que se desea realizar:

  • Modelo de efectos fijos: se utiliza cuando las conclusiones se formulan sobre un conjunto específico y previamente definido de tratamientos. En este caso, el interés estadístico se centra en comparar los efectos medios de dichos tratamientos.
  • Modelo de efectos aleatorios: se aplica cuando los tratamientos evaluados representan una muestra aleatoria de una población más amplia de tratamientos. Aquí, las conclusiones se extienden más allá de los tratamientos observados y la inferencia se centra en las varianzas asociadas a dichos tratamientos.
  • Modelo de efectos mixtos: surge cuando el experimento combina tratamientos de efectos fijos y aleatorios en un mismo estudio.

Esta clasificación permite comprender cómo las decisiones sobre el diseño experimental influyen directamente en el tipo de conclusiones que pueden extraerse, un aspecto fundamental tanto en la práctica como en la divulgación de la ingeniería.

En este archivo de audio puedes escuchar una conversación sobre los tipos de experimentos.

En este vídeo se resumen las ideas más importantes sobre este tema.

Referencias:

Anscombe, F. J. (1947). The validity of comparative experiments. Journal of the Royal Statistical Society, 61, 181–211.

Brownlee, K. A. (1957). The principles of experimental design. Industrial Quality Control, 13, 1–9.

Eisenhart, C. (1947). The assumptions underlying the analysis of variance. Biometrics, 3, 1–21.

Melo, O. O., López, L. A., & Melo, S. E. (2007). Diseño de experimentos: métodos y aplicaciones. Universidad Nacional de Colombia. Facultad de Ciencias.

Licencia de Creative Commons
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

El puente de Quebec: la doble tragedia que forjó el «Anillo de Hierro» de los ingenieros

Puente de Quebec, Canadá. Por Murielle Leclerc, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=20033047

Introducción: El puente que tuvo que caer para enseñar a construir.

Las grandes obras de la humanidad a menudo esconden historias de sacrificio y fracaso. Las estructuras que hoy admiramos por su grandeza fueron, en su momento, escenarios de tragedias que nos obligaron a aprender de la peor manera posible. Pocos ejemplos son tan crudos y reveladores como el del puente de Quebec, en Canadá. Su historia no solo es la de un colapso, sino también la de una catástrofe que sacudió los cimientos de la ingeniería y redefinió para siempre el significado de construir con responsabilidad.

La catástrofe del puente de Quebec no solo fue una tragedia de acero retorcido y vidas perdidas, sino también el catalizador que forjó una nueva conciencia ética en toda una profesión. Su legado no se mide en toneladas de acero, sino en los principios que hoy rigen la profesión de la ingeniería en Canadá y en todo el mundo.

A continuación, desvelamos cinco datos impactantes y poco conocidos sobre su catastrófica construcción que transformaron la ingeniería moderna.

1. El desastre ocurrió dos veces, no una.

La memoria colectiva recuerda el estruendoso colapso de 1907, pero la trágica historia del puente de Quebec no terminó ahí. La estructura falló catastróficamente en dos ocasiones distintas, con nueve años de diferencia entre ellas.

El primer colapso, ocurrido el 29 de agosto de 1907, se produjo durante la fase final de la construcción del brazo sur. Sin previo aviso, casi 19 000 toneladas de acero se precipitaron al río San Lorenzo en menos de 15 segundos. El estruendo fue tan violento que los habitantes de la ciudad de Quebec, situada a diez kilómetros de distancia, creyeron que se trataba de un terremoto. Murieron 75 trabajadores (otras fuentes hablan de 76). La investigación posterior determinó que la causa inmediata había sido el fallo por pandeo del cordón de compresión A9L, una viga masiva situada cerca del pilar principal, debido a un diseño deficiente de su entramado interno.

Desastre del puente de Quebec. Restos tras el colapso del tramo sur en 1907, que causó la muerte de 75 personas. Courtesy of Dominion Bridge Company Ltd./Library and Archives Canada/PA-109498

El segundo colapso (11 de septiembre de 1916) ocurrió durante el rediseño y la reconstrucción del puente. Mientras se izaba la sección central de 5000 toneladas para conectar los dos brazos del puente, se fracturó una pieza de fundición del equipo de elevación. La enorme pieza de acero se desplomó al río ante la mirada de miles de espectadores, llevándose la vida a otros trece trabajadores.

Como sombrío monumento a la tragedia, esa sección central, caída en 1916, todavía descansa en el lecho del río San Lorenzo. Este doble desastre subrayó la inmensa dificultad del proyecto y la necesidad de revisar por completo las prácticas y la ética de la ingeniería.

2. La «arrogancia» de un solo ingeniero fue la causa raíz.

El colapso de 1907 no fue un simple error de cálculo, sino que, en gran medida, fue el resultado de la soberbia profesional. La Comisión Real de Investigación, creada para analizar el desastre, señaló a un responsable principal: Theodore Cooper, uno de los ingenieros de puentes más prestigiosos de Estados Unidos de su época.

La arrogancia de Cooper se puso de manifiesto en una serie de decisiones fatales. La más grave fue ordenar, para ahorrar costes, alargar el vano principal del puente de 490 a 550 metros. Como concluyó la Comisión, se cometió «un grave error al asumir el peso muerto en los cálculos con un valor demasiado bajo y al no revisar posteriormente esta suposición». El peso real de la estructura era entre un 10 % y un 30 % mayor que el calculado, lo que constituyó un fallo directo de su supervisión. Su mala salud le impidió visitar la obra, por lo que la dirigió desde su oficina en Nueva York.

Esta negligencia se convirtió en una tragedia cuando Norman McLure, un joven ingeniero contratado por Cooper para inspeccionar la zona, empezó a enviar informes alarmantes. Las vigas de compresión inferiores, los cordones masivos que soportaban el peso, mostraban un pandeo visible, es decir, se estaban doblando. Cuando McLure se lo comunicó, la primera reacción de Cooper fue mostrarse incrédulo: «¿Cómo ha podido suceder eso?». Cooper desarrolló su propia teoría a distancia: las vigas debían haber sido golpeadas por equipos de elevación. McLure investigó y no encontró ninguna prueba. Las vigas continuaban doblándose bajo el peso mal calculado.

La arrogancia de Cooper alcanzó su punto álgido cuando Robert Douglas, un ingeniero del Gobierno canadiense, criticó las tensiones inusualmente altas de su diseño. Cooper respondió de forma tajante:

“This puts me in the position of a subordinate, which I cannot accept.”

La tragedia fue el resultado de un fallo de comunicación. El 29 de agosto, tras la insistencia de McLure, Cooper envió por fin un telegrama a la oficina de la constructora en Pensilvania en el que escribió: «No añadan más carga al puente». Sin embargo, asumió que el mensaje se transmitiría y que se detendrían los trabajos. No fue así. La gerencia del lugar ignoró la orden y decidió esperar hasta el día siguiente para actuar. A las 17:30 h de esa misma tarde, el puente se derrumbó.

3. La tragedia transformó para siempre a la comunidad Mohawk.

La catástrofe de 1907 no solo fue una tragedia de ingeniería, sino también un profundo trauma cultural para la comunidad Mohawk de Kahnawake, cuyos hombres eran reconocidos por su extraordinaria habilidad y valentía para trabajar en las alturas.

El coste humano fue devastador. De los 75 trabajadores que murieron en el primer derrumbe, 33 eran hombres Mohawk de la pequeña comunidad de Kahnawake. La pérdida fue tan grande que cuatro apellidos de la comunidad desaparecieron por completo tras la tragedia.

Lo que sucedió después fue un acto de resiliencia social sin precedentes. Las mujeres Mohawk, en un acto de «decisión matriarcal histórica», se reunieron y dictaminaron una nueva ley para proteger a su pueblo: nunca más se permitiría que los hombres de Kahnawake trabajaran todos juntos en un mismo proyecto de construcción. A partir de ese momento, debían dispersarse en pequeños grupos por toda Norteamérica.

Esta decisión tuvo una consecuencia inesperada y extraordinaria. Los herreros Mohawk se extendieron por Canadá y Estados Unidos, convirtiéndose en una fuerza laboral de élite en la construcción de los rascacielos más icónicos de Nueva York, como el Empire State Building, el Chrysler Building, el puente George Washington y, décadas después, el World Trade Center.

Anillo de hierro usado por los ingenieros canadienses – Imagen: WikiMedia.

4. El famoso anillo de hierro de los ingenieros no proviene del puente (pero la razón es más profunda).

En Canadá, los ingenieros recién graduados participan en una ceremonia solemne llamada «El Ritual de la Vocación de un Ingeniero», en la que reciben un anillo de hierro que llevan en el dedo meñique de la mano con la que escriben. Durante décadas ha circulado la poderosa leyenda de que los primeros anillos se fabricaron con el acero del puente de Quebec que se derrumbó.

Aunque es una historia bonita, es falsa. Fuentes oficiales, como «The Corporation of the Seven Wardens», que administra el ritual, confirman que se trata de un mito simbólico. Sin embargo, su verdadero origen está directamente ligado a una tragedia. El profesor H.E.T. Haultain, al sentir que la profesión necesitaba un «nexo de unión» moral, impulsó la creación de un juramento. Para ello, contó con la ayuda de una de las figuras literarias más importantes de la época: el autor y premio Nobel Rudyard Kipling.

Kipling escribió el texto del juramento (la «Obligación») y ayudó a diseñar el anillo. La primera ceremonia tuvo lugar el 25 de abril de 1925. La razón por la que se refuta activamente el mito es profunda: los anillos se fabrican con acero inoxidable estándar para garantizar que el mensaje sea la responsabilidad, no la superstición. Su superficie áspera sirve de recordatorio constante de las consecuencias de un trabajo mal hecho y del deber de servir a la humanidad por encima de todo.

Conclusión: un monumento de acero y una lección eterna.

Hoy en día, el puente de Quebec sigue en pie. Ostenta el récord del puente tipo ménsula más largo del mundo y es un eslabón vital del transporte en Canadá. Sin embargo, su verdadera grandeza no radica en sus miles de toneladas de acero, sino en las lecciones indelebles que se aprendieron de sus escombros. Es un monumento a las 88 personas que perdieron la vida en sus dos derrumbes y un recordatorio perpetuo de las consecuencias del error y de la arrogancia humana.

Su legado más duradero es invisible: los estándares éticos y la cultura de la responsabilidad que obligó a crear. El Ritual de la Vocación de un Ingeniero, nacido de su fracaso, ha sido adoptado por más de medio millón de ingenieros y se ha convertido en un poderoso símbolo de la profesión. La tragedia nos dejó una pregunta que sigue resonando hoy con más fuerza que nunca: ¿qué «puentes» estamos construyendo hoy con las nuevas tecnologías y prestando suficiente atención a las lecciones de humildad y responsabilidad que nos dejó esta tragedia de hace más de un siglo?

En este audio se recoge una conversación en la que se analizan los aspectos más relevantes de los desastres sufridos por este puente y por el Anillo de Hierro.

Este vídeo constituye una buena síntesis de las ideas fundamentales del artículo.

En este documento se sintetiza la información anterior.

Pincha aquí para descargar

Referencia:

Pearson, C., & Delatte, N. (2006). Collapse of the Quebec bridge, 1907. Journal of performance of constructed facilities, 20(1), 84-91.

Licencia de Creative Commons
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

5 lecciones sorprendentes de la IA para construir puentes más sostenibles y económicos.

La tesis doctoral leída recientemente por Lorena Yepes Bellver se centra en la optimización del diseño de puentes de losa de hormigón pretensado para pasos elevados con el fin de mejorar la sostenibilidad económica y ambiental mediante la minimización de costes, energía incorporada y emisiones de CO₂. Con el fin de reducir la elevada carga computacional del análisis estructural, la metodología emplea un marco de optimización de dos fases asistido por modelos sustitutos, en el que se destaca el uso de Kriging y redes neuronales artificiales (RNA).

En concreto, la optimización basada en Kriging condujo a una reducción de costes del 6,54 % al disminuir significativamente el consumo de hormigón y acero activo sin comprometer la integridad estructural. Si bien las redes neuronales demostraron una mayor precisión predictiva global, el modelo Kriging resultó más eficaz para identificar los óptimos locales durante el proceso de búsqueda. El estudio concluye que las configuraciones de diseño óptimas priorizan el uso de altos coeficientes de esbeltez y suponen una reducción del hormigón y del acero activo en favor del acero pasivo, con el fin de mejorar la eficiencia energética. Finalmente, la investigación integra la toma de decisiones multicriterio (MCDM, por sus siglas en inglés) para evaluar de manera integral los diseños en función de sus objetivos económicos, estructurales y ambientales.

Cuando pensamos en la construcción de grandes infraestructuras, como los puentes, suele venirnos a la mente la imagen de proyectos masivos, increíblemente caros y con un gran impacto ambiental. Son gigantes de hormigón y acero que, aunque necesarios, parecen irrenunciablemente vinculados a un alto coste económico y ecológico.

Sin embargo, ¿y si la inteligencia artificial nos estuviera mostrando un camino para que estos gigantes de hormigón fueran más ligeros, económicos y respetuosos con el planeta? Una reciente tesis doctoral sobre la optimización de puentes está desvelando hallazgos impactantes y, en muchos casos, sorprendentes. Este artículo resume esa compleja investigación en cinco lecciones clave y a menudo sorprendentes que no solo se aplican a los puentes, sino que anuncian una nueva era en el diseño de infraestructuras.

1. La sostenibilidad cuesta mucho menos de lo que crees.

Uno de los descubrimientos más importantes de la investigación es que la idea de que la sostenibilidad siempre implica un alto sobrecoste es, en gran medida, un mito. La optimización computacional demuestra que la viabilidad económica y la reducción del impacto ambiental no son objetivos opuestos.

La tesis doctoral lo cuantifica con precisión: un modesto aumento de los costes de construcción (inferior al 1 %) puede reducir sustancialmente las emisiones de CO₂ (en más de un 2 %). Este dato es muy relevante, ya que demuestra que con un diseño inteligente asistido por modelos predictivos se puede conseguir un beneficio medioambiental significativo con una inversión mínima. La sostenibilidad y la rentabilidad pueden y deben coexistir en el diseño de las infraestructuras del futuro.

2. El secreto está en la esbeltez: cuanto más fino, más eficiente.

En el diseño de un puente, la «relación de esbeltez» es un concepto clave que define la proporción entre la altura del tablero (su grosor) y la longitud del vano principal. Tradicionalmente, podríamos pensar que «más robusto es más seguro», pero la investigación demuestra lo contrario.

El estudio identificó una relación de esbeltez óptima para minimizar el impacto ambiental. Concretamente, el estudio halló una relación de esbeltez de aproximadamente 1/30 para optimizar las emisiones de CO₂ y de aproximadamente 1/28 para optimizar la energía incorporada. Esto significa que, en lugar de construir puentes masivos por defecto, los modelos de IA demuestran que un diseño más esbelto y afinado no solo es estructuralmente sólido, sino también mucho más eficiente en el uso de materiales. Este diseño más esbelto se logra no solo usando menos material en general, sino también mediante un sorprendente reequilibrio entre los componentes clave de la estructura, como veremos a continuación.

3. El equilibrio de materiales: menos hormigón, más acero (pasivo).

Quizás uno de los descubrimientos más sorprendentes es que el diseño más sostenible no consiste simplemente en utilizar menos cantidad de todos los materiales. La solución óptima es más un reequilibrio inteligente que una simple reducción general.

La investigación revela que los diseños optimizados lograron reducir el uso de hormigón en un 14,8 % y de acero activo (el acero de pretensado que tensa la estructura) en un 11,25 %. Sin embargo, este descenso se compensa con un aumento de la armadura pasiva (el acero convencional que refuerza el hormigón). Esto resulta contraintuitivo, ya que la intuición ingenieril a menudo favorece una reducción uniforme de los materiales. Sin embargo, los modelos computacionales identifican un complejo intercambio —sacrificar un material más barato (hormigón) por otro más caro (acero pasivo)— para alcanzar un diseño globalmente óptimo en términos de coste y emisiones de CO₂, un equilibrio que sería extremadamente difícil de lograr con métodos de diseño tradicionales.

4. Precisión frente a dirección: El verdadero poder de los modelos predictivos.

Al comparar diferentes modelos de IA, como las redes neuronales artificiales y los modelos Kriging, la tesis doctoral reveló una lección fundamental sobre su verdadero propósito en ingeniería.

El estudio reveló que, si bien las redes neuronales ofrecían predicciones absolutas más precisas, el modelo Kriging era más eficaz para identificar las regiones de diseño óptimas. Esto pone de manifiesto un aspecto crucial sobre el uso de la IA en el diseño: su mayor potencial no radica en predecir un valor exacto, como si fuera una bola de cristal, sino en guiar al ingeniero hacia la «región» del diseño donde se encuentran las mejores soluciones posibles. La IA es una herramienta de exploración y dirección que permite navegar por un universo de posibilidades para encontrar de forma eficiente los diseños más prometedores.

5. La optimización va directo al bolsillo: reducción de costes superior al 6 %.

Más allá de los objetivos medioambientales, la investigación demuestra que estos modelos de IA son herramientas muy potentes para la optimización económica directa. Este descubrimiento no se refiere al equilibrio entre coste y sostenibilidad, sino a la reducción pura y dura de los costes del proyecto.

La tesis doctoral muestra que el método de optimización basado en Kriging consigue una reducción de costes del 6,54 %. Esta importante reducción se consigue principalmente minimizando el uso de materiales: un 14,8 % menos de hormigón y un 11,25 % menos de acero activo, el acero de pretensado más especializado y costoso. Esto demuestra de forma contundente que los modelos sustitutivos no solo sirven para alcanzar metas ecológicas, sino que también son una herramienta de gran impacto para la optimización económica en proyectos a gran escala.

Conclusión: Diseñando el futuro, un puente a la vez.

La inteligencia artificial y los modelos de optimización han dejado de ser conceptos abstractos para convertirse en herramientas prácticas que permiten descubrir formas novedosas y eficientes de construir la infraestructura del futuro. Los resultados de esta investigación demuestran que es posible diseñar y construir puentes que sean más económicos y sostenibles al mismo tiempo.

Estos descubrimientos no solo se aplican a los puentes, sino que abren la puerta a una nueva forma de entender la ingeniería. Si la IA puede rediseñar algo tan grande como un puente para hacerlo más sostenible, ¿qué otras grandes industrias están a punto de transformarse con un enfoque similar?

En este audio podéis escuchar una conversación sobre este tema.

Este vídeo resume las ideas principales.

Aquí tenéis un documento resumen de las ideas básicas.

Pincha aquí para descargar

Referencias:

YEPES-BELLVER, L.; ALCALÁ, J.; YEPES, V. (2025). Predictive modeling for carbon footprint optimization of prestressed road flyovers. Applied Sciences, 15(17), 9591. DOI:10.3390/app15179591

VILLALBA, P.; SÁNCHEZ-GARRIDO, A.; YEPES-BELLVER, L.; YEPES, V. (2025). A Hybrid Fuzzy DEMATEL–DANP–TOPSIS Framework for Life Cycle-Based Sustainable Retrofit Decision-Making in Seismic RC Structures. Mathematics, 13(16), 2649. DOI:10.3390/math13162649

ZHOU, Z.; WANG, Y.J.; YEPES-BELLVER, L.; ALCALÁ, J.; YEPES, V. (2025). Intelligent monitoring of loess landslides and research on multi-factor coupling damage. Geomechanics for Energy and the Environment, 42:100692. DOI:10.1016/j.gete.2025.100692

ZHOU, Z.; YEPES-BELLVER, L.; ALCALÁ, J.; YEPES, V. (2025). Study on the failure mechanism of deep foundation pit of high-rise building: comprehensive test and microstructure coupling. Buildings, 15(8), 1270. DOI:10.3390/buildings15081270

YEPES-BELLVER, L.; BRUN-IZQUIERDO, A.; ALCALÁ, J.; YEPES, V. (2025). Surrogate-assisted cost optimization for post-tensioned concrete slab bridges. Infrastructures, 10(2): 43. DOI:10.3390/infrastructures10020043.

BLIGHT, T.; MARTÍNEZ-PAGÁN, P.; ROSCHIER, L.; BOULET, D.; YEPES-BELLVER, L.; YEPES, V. (2025). Innovative approach of nomography application into an engineering educational context. Plos One, 20(2): e0315426. DOI:10.1371/journal.pone.0315426

NAVARRO, I.J.; VILLALBA, I.; YEPES-BELLVER, L.; ALCALÁ, J. Social Life Cycle Assessment of Railway Track Substructure Alternatives. J. Clean. Prod. 2024, 450, 142008.

YEPES-BELLVER, L.; BRUN-IZQUIERDO, A.; ALCALÁ, J.; YEPES, V. (2024). Artificial neural network and Kriging surrogate model for embodied energy optimization of prestressed slab bridges. Sustainability, 16(19), 8450. DOI:10.3390/su16198450

YEPES-BELLVER, L.; BRUN-IZQUIERDO, A.; ALCALÁ, J.; YEPES, V. (2023). Embodied energy optimization of prestressed concrete road flyovers by a two-phase Kriging surrogate model. Materials, 16(20); 6767. DOI:10.3390/ma16206767

YEPES-BELLVER, L.; BRUN-IZQUIERDO, A.; ALCALÁ, J.; YEPES, V. (2022). CO₂-optimization of post-tensioned concrete slab-bridge decks using surrogate modeling. Materials, 15(14):4776. DOI:10.3390/ma15144776

Licencia de Creative Commons
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

3 secretos sorprendentes detrás de las encuestas que rellenas cada día.

Introducción: La ciencia oculta de las encuestas.

Todos hemos pasado por ello: cuestionarios interminables, preguntas que parecen sacadas de un manual de psicología y, sobre todo, esa sensación de responder a la misma pregunta una y otra vez. Es una experiencia tan común como, a menudo, frustrante. ¿Por qué algunas preguntas parecen extrañas o repetitivas? ¿Realmente merece la pena todo este esfuerzo?

La respuesta es un rotundo sí. Detrás de cada cuestionario bien diseñado se esconde la rigurosa ciencia de la psicometría, el campo dedicado al arte de la medición precisa. Conceptos como la fiabilidad y la validez son los pilares de cualquier instrumento de medición serio, ya sea una encuesta de satisfacción del cliente o un test de personalidad.

Este artículo desvela algunos de los secretos más sorprendentes y fascinantes sobre cómo se construyen estas escalas de medida. Descubrirás por qué la repetición puede ser una virtud, por qué la perfección a veces es sospechosa y por qué es posible equivocarse de manera confiable.

Primer secreto: la fiabilidad no es la validez (y se puede estar fiablemente equivocado).

En el mundo de la medición, la fiabilidad y la validez son dos conceptos cruciales que a menudo se confunden. Sin embargo, comprender su diferencia es fundamental para entender por qué algunas encuestas funcionan y otras no.

  • La fiabilidad se refiere a la precisión o consistencia de una medida. Un instrumento fiable produce resultados muy similares cada vez que se utiliza en las mismas condiciones.
  • La validez es la exactitud de la medida. Un instrumento válido mide exactamente lo que se pretende medir. La validez va más allá de la simple exactitud, ya que se asegura de que las conclusiones que extraemos de los resultados de la encuesta estén justificadas y sean significativas.

La mejor manera de entenderlo es mediante la analogía de un tirador que apunta a una diana.

  • Fiabilidad sin validez: imagina a un tirador. Escuchas el sonido seco y repetitivo de los disparos impactando en la madera, agrupados en un área no mayor que una moneda, pero peligrosamente cerca del borde de la diana. El patrón es muy consistente (alta fiabilidad), pero erróneo de forma sistemática, ya que no alcanza el blanco (baja validez). Esto representa un error sistemático que se debe a un defecto fundamental en el diseño del cuestionario, como preguntas mal redactadas o una escala de respuesta poco clara.
  • Validez con baja fiabilidad: ahora imagina a un tirador cuyos disparos están dispersos por toda la diana, pero cuya media se sitúa justo en el centro. No hay precisión en cada tiro (baja fiabilidad), pero, en conjunto, apuntan en la dirección correcta (alta validez). Esto representa errores aleatorios que pueden deberse a factores incontrolables, como distracciones, ruido ambiental o incluso al estado de ánimo temporal del encuestado.
Validez y fiabilidad (Morales, 2008)

La conclusión clave es que la validez es más importante que la fiabilidad. Como subrayan los expertos en la materia: «Un instrumento puede ser muy fiable (medir muy bien), pero no medir bien lo que se quería medir». De nada sirve medir algo con una precisión milimétrica si no es lo que realmente nos interesa.

Segundo secreto: ¿por qué las encuestas a veces parecen repetitivas?

Una de las quejas más comunes sobre los cuestionarios es que incluyen preguntas que parecen decir lo mismo de distintas maneras. Lejos de ser un descuido, el uso de lo que los expertos denominan «ítems repetitivos» —expresar la misma idea de diversas formas— es una técnica deliberada y muy útil para garantizar la calidad de los datos. Esta «forma bidireccional de redactar los ítems» tiene dos ventajas principales:

  • Requiere mayor atención del sujeto: al presentar la misma idea con formulaciones distintas (a veces en positivo y otras en negativo), se evita que la persona responda de forma automática o sin pensar y se le obliga a procesar el significado de cada pregunta.
  • Permite comprobar la coherencia de las respuestas: sirve como control de calidad para detectar y mitigar dos de los sesgos más frecuentes al responder encuestas: la aquiescencia y el sesgo de confirmación.
    • Aquiescencia: tendencia a estar de acuerdo con todas las afirmaciones. Imagina a alguien que responde con prisas, marcando «Totalmente de acuerdo» a todo («Sí, el servicio fue excelente», «Sí, el producto es terrible»), con el único fin de terminar cuanto antes.
    • Deseabilidad social: tendencia a responder para proyectar una buena imagen. Este sesgo lo muestra la persona que, al ser preguntada por sus hábitos de reciclaje, se presenta como un ecologista modelo, aunque el contenido de su cubo de basura cuente una historia muy diferente.

Por lo tanto, la próxima vez que te encuentres con preguntas que te resulten familiares en un mismo cuestionario, recuerda que no se trata de un error. Se trata de una herramienta diseñada para garantizar que tus respuestas sean más atentas, coherentes y, en última instancia, sinceras.

Tercer secreto: una fiabilidad «perfecta» puede ser una señal de alarma.

Intuitivamente, podríamos pensar que el objetivo de cualquier escala de medida es lograr la mayor fiabilidad posible. Sin embargo, en psicometría, una fiabilidad extremadamente alta puede ser una señal de alarma que indica un problema subyacente.

El coeficiente de fiabilidad más utilizado, el alfa de Cronbach, presenta una particularidad: su valor tiende a aumentar al añadir más ítems a la escala. Esto crea la tentación de inflar artificialmente la fiabilidad simplemente alargando el cuestionario. Como advierte la literatura especializada: «No se debe buscar una alta fiabilidad aumentando sin más el número de ítems, sin pensar si realmente son válidos».

Un ejemplo hipotético ilustra perfectamente este peligro. Imaginemos que aplicamos un test a un grupo mixto compuesto por niñas de 10 años que hacen ballet y niños de 14 años que juegan al fútbol. Les preguntamos por su edad, su sexo y el deporte que practican. La fiabilidad estadística se dispara porque las preguntas son perfectamente consistentes al separar a los dos grupos. Si se pregunta sobre ballet, todas las niñas responden de una manera y todos los niños de otra. Si se pregunta por el fútbol, ocurre lo mismo. El algoritmo estadístico detecta esta consistencia impecable y reporta una fiabilidad altísima, sin comprender que el «rasgo» subyacente que se está midiendo es simplemente una mezcla de datos demográficos, no una característica psicológica coherente. A pesar de esa elevada fiabilidad, en realidad no estaríamos midiendo «nada interpretable».

Este ejemplo nos deja una lección fundamental que el texto fuente resume de manera brillante:

«En ningún caso la estadística sustituye al sentido común y al análisis lógico de nuestras acciones».

Conclusión: la próxima vez que rellenes una encuesta…

Desde el dilema fundamental entre mediciones consistentes, pero erróneas (fiabilidad frente a validez), pasando por el uso deliberado de la repetición para burlar nuestros propios sesgos, hasta la idea contraintuitiva de que una puntuación «perfecta» puede indicar un resultado sin sentido, queda claro que elaborar una buena encuesta es un trabajo científico.

La próxima vez que te enfrentes a un cuestionario, en lugar de frustrarte por sus preguntas, ¿te detendrás a pensar qué rasgo intentan medir y si realmente lo están logrando?

En este audio os dejo una conversación sobre estas ideas.

Os dejo un vídeo que resume el contenido de este artículo.

Referencias:

Campbell, D. T., & Fiske, D. W. (1959). Convergent and discriminant validation by the multitrait–multimethod matrix. Psychological Bulletin, 56(2), 81–105. https://doi.org/10.1037/h0046016

Dunn, T. J., Baguley, T., & Brunsden, V. (2014). From alpha to omega: A practical solution to the pervasive problem of internal consistency estimation. British Journal of Psychology, 105, 399–412. https://doi.org/10.1111/bjop.12046

Farrell, A. M. (2010). Insufficient discriminant validity: A comment on Bove, Pervan, Beatty and Shiu (2009). Journal of Business Research, 63, 324–327. https://ssrn.com/abstract=3466257

Fornell, C., & Larcker, D. F. (1981). Evaluating structural equation models with unobservable variables and measurement error. Journal of Marketing Research, 18(1), 39–50. https://doi.org/10.1177/002224378101800104

Frías-Navarro, D. (2019). Apuntes de consistencia interna de las puntuaciones de un instrumento de medida. Universidad de Valencia. https://www.uv.es/friasnav/AlfaCronbach.pdf

Grande, I., & Abascal, E. (2009). Fundamentos y técnicas de investigación comercial. Madrid: ESIC.

Hernández, B. (2001). Técnicas estadísticas de investigación social. Madrid: Díaz de Santos.

Hair, J. F., Anderson, R. E., Tatham, R. L., & Black, W. C. (1995). Multivariate data analysis (Eds.). New York: Prentice Hall International, Inc.

Kotler, P., & Armstrong, G. (2001). Marketing. México: Pearson Prentice Hall.

Matas, A. (2018). Diseño del formato de escalas tipo Likert: un estado de la cuestión. Revista Electrónica de Investigación Educativa, 20(1), 38–47. http://www.scielo.org.mx/scielo.php?script=sci_arttext&pid=S1607-40412018000100038

Morales, P. (2006). Medición de actitudes en psicología y educación. Madrid: Universidad Pontificia de Comillas.

Morales, P. (2008). Estadística aplicada a las ciencias sociales. Madrid: Universidad Pontificia Comillas.

Nadler, J., Weston, R., & Voyles, E. (2015). Stuck in the middle: The use and interpretation of mid-points in items on questionnaires. The Journal of General Psychology, 142(2), 71–89. https://doi.org/10.1080/00221309.2014.994590

Nunnally, J. C. (1978). Psychometric theory. New York: McGraw-Hill.

Schmitt, N. (1996). Uses and abuses of coefficient alpha. Psychological Assessment, 8(4), 350–353. http://ist-socrates.berkeley.edu/~maccoun/PP279_Schmitt.pdf

Prats, P. (2005). Métodos para medir la satisfacción del cliente. Madrid: AENOR Ediciones.

Licencia de Creative Commons
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.