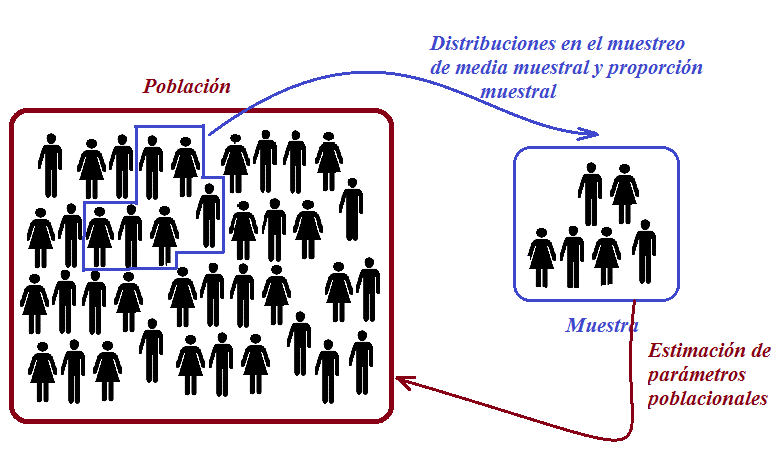
En cualquier investigación estadística, se recopila información de un conjunto de elementos específicos. Una población se define como un conjunto completo de posibles individuos, especímenes, objetos o medidas de interés que se someten a un estudio para ampliar nuestro conocimiento sobre ellos. En el caso de poblaciones finitas y de tamaño reducido, es factible medir a todos los individuos para obtener un conocimiento preciso de sus características, también conocidas como parámetros. Por ejemplo, se podría analizar la proporción de productos defectuosos o calcular la media de alguna variable relacionada con los productos.
Por otro lado, cuando la población es infinita o muy numerosa, resulta impracticable o costoso medir a todos los individuos. En tales circunstancias, es necesario extraer una muestra representativa de la población y, basándonos en las características observadas en dicha muestra (conocidas como estadísticos), podemos realizar inferencias sobre los parámetros que describen a la población en su totalidad. De manera figurativa, podríamos comparar una muestra, que se supone representativa de una población, con lo que una maqueta representa respecto al edificio que retrata. La calidad de la muestra, al igual que la de la maqueta, dependerá del grado de representatividad que pueda ofrecer.
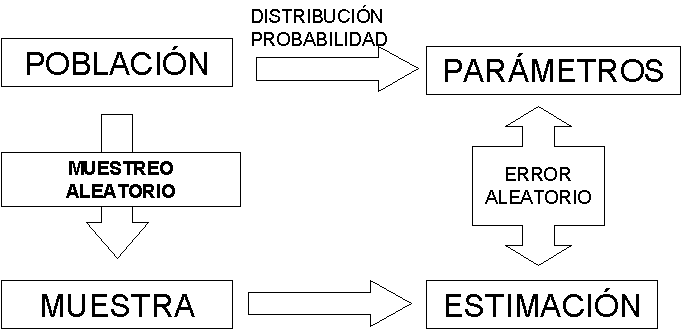
En términos generales, la inferencia estadística es el proceso de utilizar estadísticos de una muestra para hacer deducciones acerca de la distribución de probabilidad de una población. Si estas deducciones se efectúan sobre parámetros poblacionales, este proceso se denomina inferencia estadística paramétrica. Si las deducciones se hacen sobre la distribución de probabilidad completa, sin hacer referencia a parámetros específicos, se le llama inferencia estadística no paramétrica.
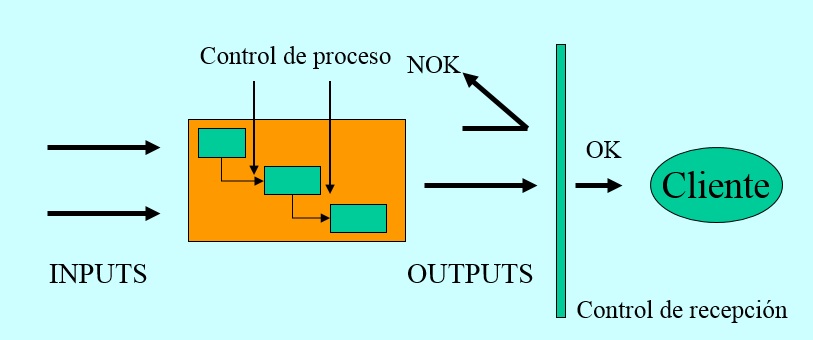
Dentro del ámbito industrial, las poblaciones de interés abarcan una amplia gama de elementos, que incluyen materiales, productos terminados, partes o componentes, así como procesos, entre otros. En muchas ocasiones, estas poblaciones se caracterizan por ser infinitas o de gran magnitud. Por ejemplo, en la elaboración del hormigón en una planta, resulta inviable, o al menos poco práctico, medir la resistencia a la compresión simple de cada una de las muestras que podrían obtenerse en una amasada. Incluso en situaciones donde la producción no sea masiva, es recomendable pensar en el proceso como si fuera una población infinita o de gran escala, dado que la producción puede continuar sin interrupciones, es decir, no existe un último artículo mientras la empresa siga en funcionamiento. Un ejemplo sería la fabricación de bloques de hormigón en una empresa de prefabricados. En tales circunstancias, los procesos se evalúan mediante muestras de productos extraídas en algún punto específico del proceso.
Un punto crucial a considerar es la obtención de muestras que sean verdaderamente representativas, es decir, que capturen de manera adecuada los aspectos clave que se desean analizar en la población. Para lograr esta representatividad, resulta esencial diseñar un proceso de muestreo aleatorio de manera apropiada. En este tipo de muestreo, se evita cualquier tipo de sesgo que pudiera favorecer la inclusión de elementos particulares, asegurando que todos los elementos de la población tengan las mismas oportunidades de formar parte de la muestra.
Existen varias técnicas de muestreo aleatorio, como el muestreo simple, el muestreo estratificado, el muestreo sistemático y el muestreo por conglomerados. Cada una de estas metodologías se adapta a los objetivos específicos del estudio, así como a las circunstancias y características particulares de la población, garantizando de esta manera que las muestras obtenidas sean verdaderamente representativas.
No obstante, en la práctica, la hipótesis de un muestreo aleatorio suele quedar lejos de cumplirse al lidiar con datos del mundo real. Un ejemplo ilustrativo son los registros de la temperatura diaria. En estos registros, los días calurosos tienden a agruparse, lo que significa que los valores elevados tienden a seguir a otros valores elevados. A este fenómeno se le denomina autocorrelación, y por ende, estos datos no pueden considerarse como el resultado de extracciones aleatorias. La validez de la hipótesis de muestreo aleatorio desempeña un papel fundamental tanto en el análisis como en el diseño de experimentos científicos o en el ámbito del control de la calidad.
La importancia de la aleatoriedad se destaca de manera clara en situaciones cotidianas. Por ejemplo, al seleccionar una muestra de ladrillos de un palet, si optamos por los que se encuentran en la parte superior, podríamos introducir un sesgo en nuestros resultados. Es lamentable que en muchos trabajos estadísticos, la hipótesis de muestreo aleatorio se trate como si fuera una característica inherente de los datos naturales. En realidad, cuando trabajamos con datos reales, la aleatoriedad no es una propiedad en la que podamos confiar de manera absoluta. Sin embargo, con las precauciones adecuadas en el diseño experimental o en la toma de muestras de un control estadístico de la calidad, esta suposición puede seguir siendo relevante y útil.
Os dejo a continuación un vídeo explicativo, que espero os sea de interés.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.