En un artículo anterior describimos la metaheurística conocida como “Recocido simulado” o “Cristalización simulada”, que en inglés se conoce como “Simulated Annealing”. Para los que no estéis familiarizados con la optimización, os dejo en este enlace una descripción de lo que son las metaheurísticas.
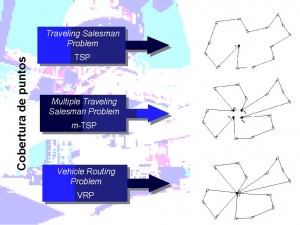
En la década de 1980, Kirkpatrick et al. (1983), mientras trabajaban en el diseño de circuitos electrónicos, y de manera independiente, Cerny (1985), investigando el problema del TSP (Traveling Salesman Problem), consideraron la aplicación del algoritmo de Metrópolis en algunos de los desafíos de optimización combinatoria que surgen en este tipo de diseño. Para lograrlo, creyeron que era posible establecer una analogía entre los parámetros presentes en la simulación termodinámica y aquellos que se encuentran en los métodos de optimización local. En la Figura 2 se puede ver dicha analogía.
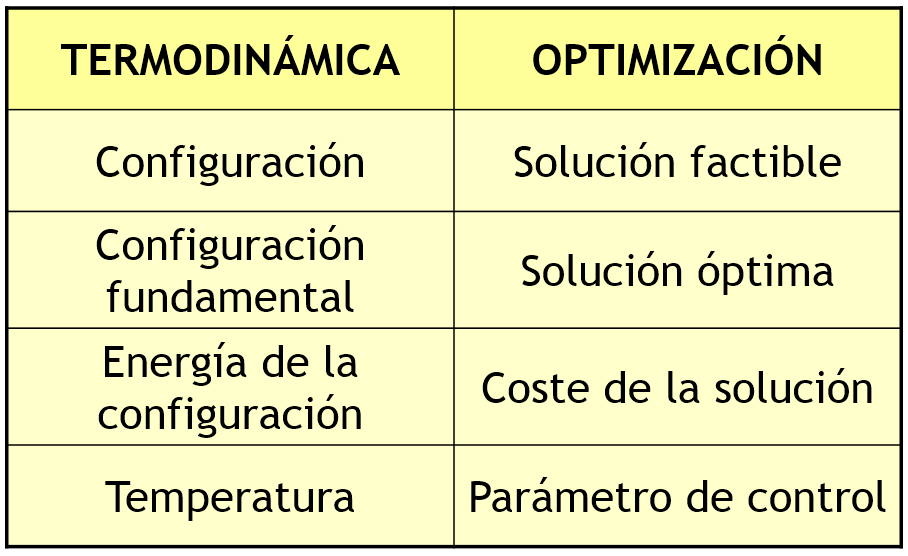
Como se puede observar, en el ámbito de la optimización, el concepto físico de temperatura no tiene un significado literal, sino que debe ser considerado como un parámetro, T, que necesita ser ajustado. De esta manera, podemos encontrar similitudes entre los procesos que tienen lugar cuando las moléculas de una sustancia se distribuyen en diferentes niveles energéticos en busca de un equilibrio a una temperatura específica y los procesos de minimización en la optimización local (o, en el caso de maximización, de manera similar).
En el primer caso, con una temperatura fija, la distribución de las partículas sigue la distribución de Boltzmann. Por lo tanto, cuando una molécula se desplaza, su movimiento será aceptado en la simulación si esto resulta en una disminución de la energía, o con una probabilidad proporcional al factor de Boltzmann si no es así. En el contexto de la optimización, al fijar el parámetro T, introducimos una perturbación y aceptamos directamente la nueva solución si su costo disminuye, o bien con una probabilidad proporcional al “factor de Boltzmann” en caso contrario.
La clave del recocido simulado es su estrategia heurística de búsqueda local. La elección del nuevo elemento del entorno, N(s), se hace de manera aleatoria, lo que puede llevar a quedar atrapado en óptimos locales. Para evitar esto, el recocido simulado permite, con una probabilidad decreciente a medida que nos acercamos a la solución óptima, el movimiento hacia soluciones peores. Al analizar el factor de Boltzmann en función de la temperatura, observamos que a medida que esta disminuye, la probabilidad de aceptar una solución peor disminuye rápidamente.
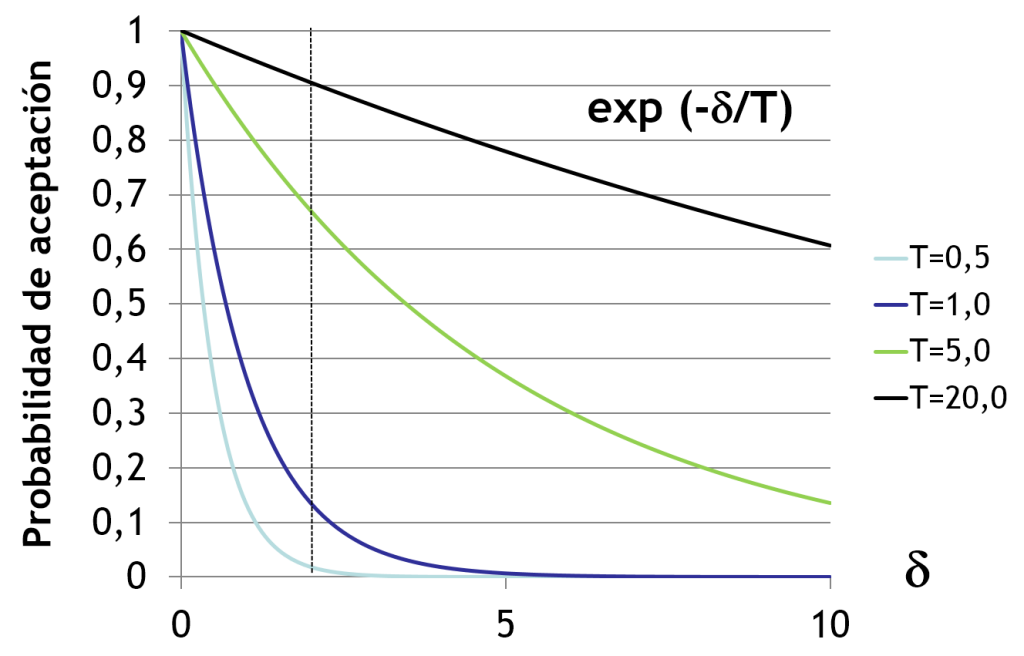
En consecuencia, la estrategia a seguir en el recocido simulado implica comenzar con una temperatura alta. Esto permite la posibilidad de aceptar soluciones peores en las primeras etapas, cuando estamos a gran distancia del óptimo global. A medida que se avanza hacia el óptimo global, se reducirá gradualmente la temperatura, disminuyendo así la probabilidad de aceptar soluciones peores. El nombre de este algoritmo proviene del proceso metalúrgico de “recocido” utilizado, por ejemplo, para eliminar las tensiones internas en el acero laminado en frío. En este proceso, el material se somete a un calentamiento rápido y luego se enfría de manera lenta y controlada durante horas.
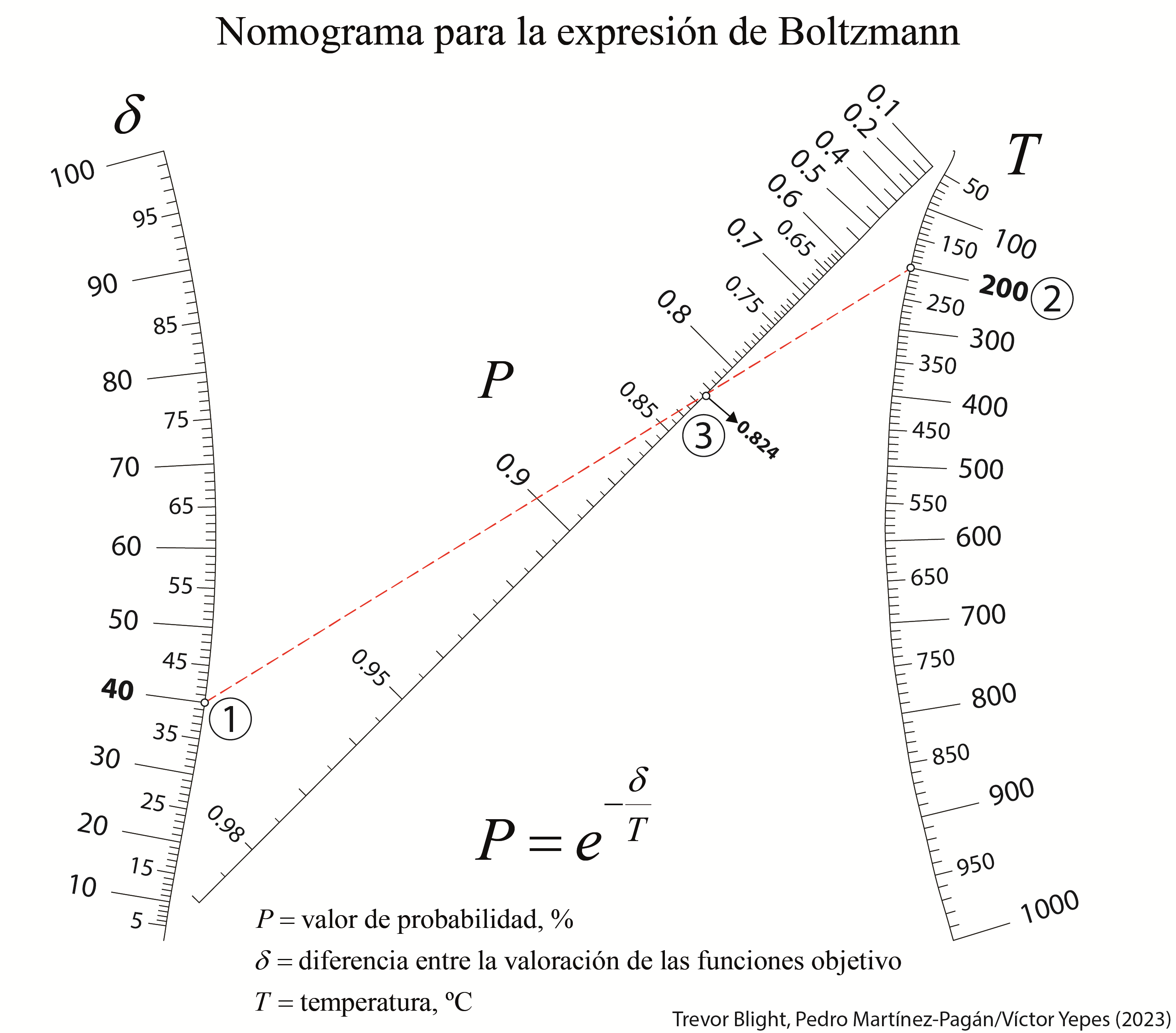
A continuación os dejo un nomograma, elaborado junto con los profesores Trevor Blight y Pedro Martínez Pagán, para calcular la probabilidad en función de la temperatura y de δ. Aquí también resulta sencillo comprobar cómo varía dicha probabilidad en función de los valores anteriores.
Os dejo también un vídeo explicativo:
Referencias
CERNY, V. (1985). Thermodynamical approach to the traveling salesman problem: an efficient simulated algorithm. Journal of Optimization Theory and Applications, 45: 41-51.
DÍAZ, A. et al. (1996). Optimización heurística y redes neuronales en dirección de operaciones e ingeniería. Editorial Paraninfo, Madrid, 235 pp.
KIRKPATRICHK, S.; GELATT, C.D.; VECCHI, M.P. (1983). Optimization by simulated annealing. Science, 220(4598): 671-680.
LUNDY, M.; MEES, A. (1986). Convergence of an Annealing Algorithm. Mathematical programming, 34:111-124.
METROPOLIS, N.; ROSENBLUTH, A.W.; ROSENBLUTH, M.N.; TELLER, A.H.; TELER, E. (1953). Equation of State Calculation by Fast Computing Machines. Journal of Chemical Physics, 21:1087-1092.
GONZÁLEZ-VIDOSA-VIDOSA, F.; YEPES, V.; ALCALÁ, J.; CARRERA, M.; PEREA, C.; PAYÁ-ZAFORTEZA, I. (2008) Optimization of Reinforced Concrete Structures by Simulated Annealing. TAN, C.M. (ed): Simulated Annealing. I-Tech Education and Publishing, Vienna, pp. 307-320. (link)

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.