En los artículos de este blog sobre resiliencia y cambio climático que estoy escribiendo, me centraré en los aspectos relacionados con la resiliencia comunitaria.
En los artículos de este blog sobre resiliencia y cambio climático que estoy escribiendo, me centraré en los aspectos relacionados con la resiliencia comunitaria.
Acontecimientos como las inundaciones catastróficas ocurridas en la provincia de Valencia el 29 de noviembre de 2024 ponen de manifiesto la importancia de estas ideas.
Estas reflexiones se enmarcan dentro del proyecto RESILIFE que desarrollo en la actualidad como investigador principal, y se han basado en algunas ideas desarrolladas en el trabajo reciente de Ellingwood et al. (2024).
Este artículo trata sobre la resiliencia comunitaria y cómo incorporar los efectos del cambio climático en la planificación y diseño de edificios e infraestructuras a nivel comunitario. Se discuten los desafíos y consideraciones clave para lograr una mayor resiliencia de las comunidades frente a eventos climáticos extremos.
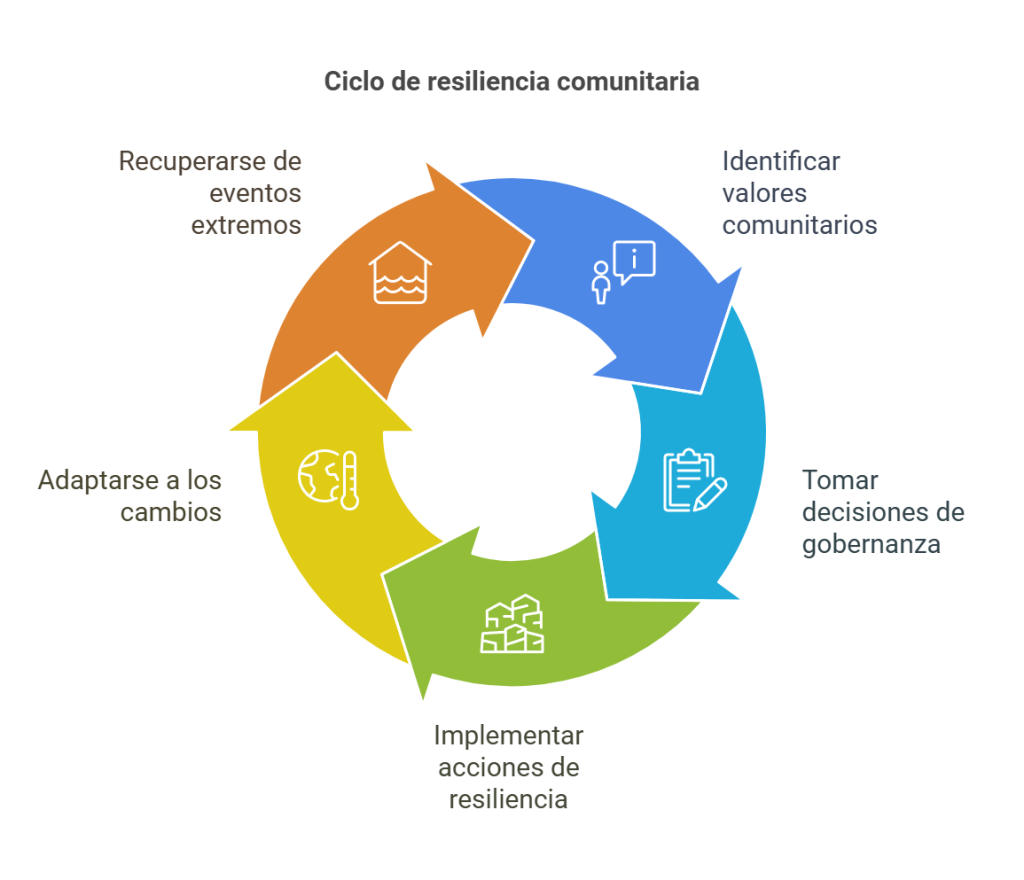
La resiliencia comunitaria es la capacidad para adaptarse a las situaciones adversas, adaptarse a condiciones cambiantes y mantener sus funciones e infraestructuras fundamentales, así como recuperarse rápidamente ante eventos extremos. En este contexto, «comunidad» se refiere a un lugar delimitado por fronteras geográficas que opera bajo la jurisdicción de una estructura de gobernanza, como una ciudad, área metropolitana o región. Es dentro de esta gobernanza local donde se identifican, aprueban, financian y ponen en marcha las decisiones, acciones y proyectos relacionados con la resiliencia. Este concepto subraya la importancia de guiar los procesos adaptativos dentro de la comunidad para preservar su identidad básica y permitir los cambios necesarios con el tiempo. La identidad de una comunidad la forman los valores y prioridades de sus miembros, por lo que los esfuerzos para aumentar la resiliencia deben implicarles en la definición de lo que valoran colectivamente y lo que pretenden proteger (Ellingwood et al., 2024).
Las repercusiones económicas del cambio climático varían mucho, con beneficios potenciales en las regiones templadas a niveles más bajos de calentamiento, pero con pérdidas crecientes a medida que aumentan las temperaturas. Los hogares y los países más pobres pueden experimentar efectos desproporcionados sobre su bienestar, aun cuando sus contribuciones económicas sean menos significativas. Las respuestas de adaptación efectivas, como el desarrollo de infraestructuras resilientes y tecnologías climáticamente inteligentes, pueden ayudar a mitigar estos impactos y mejorar la resiliencia de las comunidades (O’Neill et al., 2022).
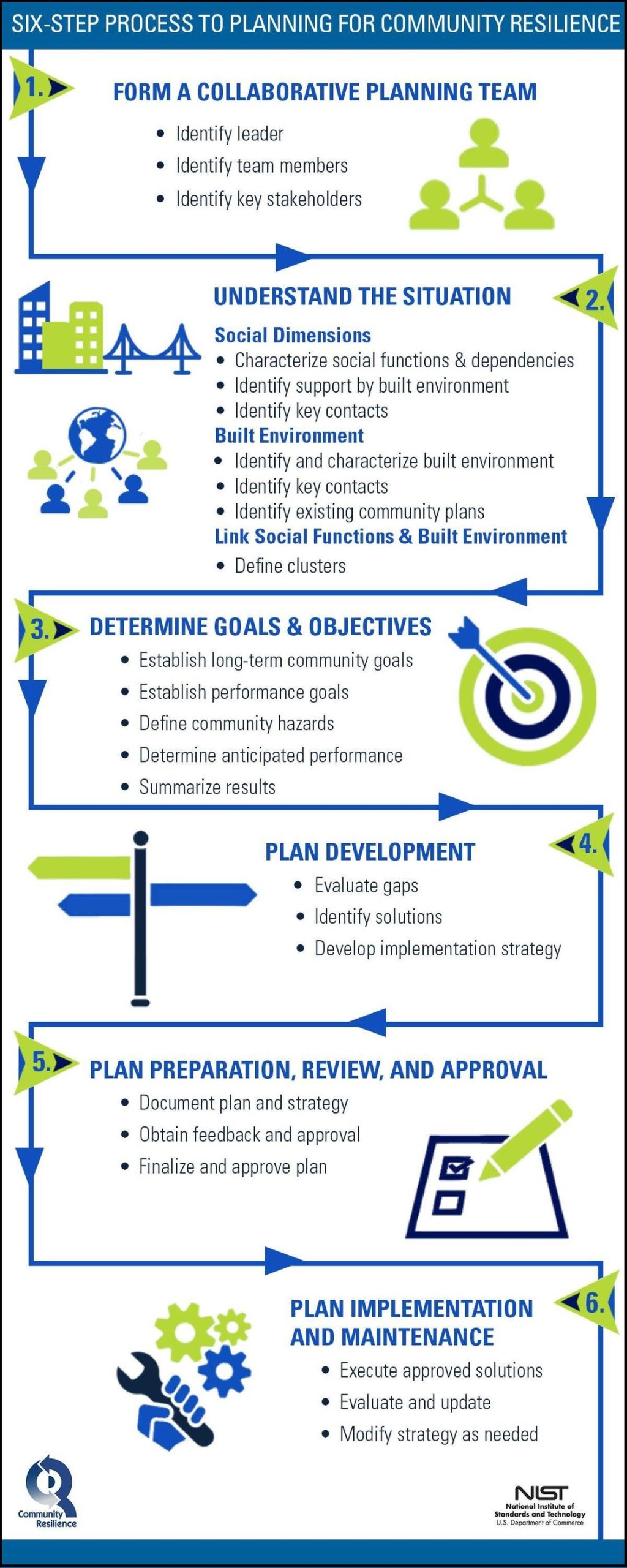
El éxito de la resiliencia comunitaria no solo se centra en la recuperación de eventos relacionados con el cambio climático, sino que también abarca una variedad más amplia de retos, incluidos los sociales y económicos. Este concepto influye en las decisiones relativas al entorno construido, que abarca desde instalaciones individuales hasta sistemas de infraestructura regional. Para que la planificación de la resiliencia sea efectiva, es crucial incluir diversas perspectivas de las partes interesadas y comprender los sistemas sociales, políticos y económicos de la comunidad, así como sus vulnerabilidades inherentes (Eisenhauer et al., 2024). El entorno construido abarca todos los sistemas diseñados en una comunidad o región, como edificios, instalaciones y redes de infraestructura. Aunque muchas viviendas unifamiliares no son diseñadas por ingenieros, deben tenerse en cuenta en la evaluación de la resiliencia comunitaria. Este enfoque integrado permite identificar los objetivos de rendimiento de los edificios e infraestructuras y garantizar que las estrategias de resiliencia se adapten a las necesidades específicas de la comunidad.
Para lograr resiliencia a nivel comunitario, los edificios y sistemas de infraestructura deben cumplir los criterios de resiliencia establecidos a nivel local. Esta interdependencia entre escalas diferentes de resiliencia conecta la planificación regional con el diseño de infraestructuras individuales. Para que las instalaciones y los sistemas den un paso adelante y alcancen un desempeño resiliente, es necesario ir más allá de los requisitos de códigos y normas actuales, que se centran principalmente en la seguridad de las personas y en limitar el fallo estructural, especialmente en la recuperación de la funcionalidad. Los edificios e infraestructuras proporcionan refugio, servicios básicos y otros recursos, como escuelas y hospitales, y respaldan instituciones sociales y económicas esenciales para el bienestar de la comunidad.
Para desarrollar planes sólidos de resiliencia comunitaria, es fundamental involucrar a las partes interesadas. Una oficina dedicada a la resiliencia puede garantizar un liderazgo firme y un compromiso coherente entre los agentes locales. Es crucial comprender la identidad y los recursos únicos de la comunidad, así como fomentar la participación de los líderes sociales (Eisenhauer et al., 2024). Incluir las voces de todos los miembros de la comunidad en el proceso de planificación hace que los esfuerzos de resiliencia sean más equitativos y eficaces.
La resiliencia comunitaria se enfrenta a diversas limitaciones que deben abordarse para mejorar su capacidad de adaptación. Entre estas dificultades se encuentran las barreras económicas, los factores sociales y culturales, las limitaciones de capacidad humana, los problemas de gobernanza, los recursos financieros, la accesibilidad a la información, los obstáculos físicos y las influencias climáticas (O’Neill et al., 2022). Reconocer y superar estas limitaciones es fundamental para que las comunidades desarrollen su capacidad de adaptación ante amenazas actuales y emergentes.
Los sectores vulnerables dentro de las comunidades suelen verse afectados de manera desproporcionada por los peligros derivados del cambio climático, como las inundaciones, debido a políticas de uso del suelo, desventajas económicas y otros factores demográficos, como la raza/etnia, el género y la edad. Por lo tanto, los objetivos de resiliencia pueden variar de una comunidad a otra debido a diferencias en las características sociodemográficas, la edad y el estado de los edificios e infraestructuras, así como a los enfoques adoptados para abordar la equidad en los objetivos de resiliencia.
El cambio climático no solo afecta a los medios de subsistencia físicos, sino que también amenaza las estructuras sociales y las prácticas culturales. La erosión del capital social, exacerbada por la degradación de los recursos y la competencia, puede provocar un aumento de la tensión en el seno de las comunidades y entre ellas, lo que puede dar lugar a conflictos y migraciones forzosas. Los grupos vulnerables, como las personas mayores y con discapacidad, se ven afectados de forma desproporcionada por estos cambios, lo que subraya la necesidad de estrategias de adaptación específicas (IPCC, 1997) .
Consideraciones de proyecto para la resiliencia y los impactos climáticos
La consideración de eventos climáticos extremos futuros (como huracanes, olas de calor y precipitaciones intensas) está cobrando una importancia cada vez mayor para las comunidades. Aunque actualmente no se tienen en cuenta en los códigos o normas de construcción, muchas comunidades locales exigen que los efectos climáticos se integren en los proyectos. (Vogel et al., 2016). Además, el cambio climático puede agravar los impactos de los eventos de peligro extremo con el tiempo, no solo al modificar las cargas sobre las estructuras, sino también al afectar a su capacidad debido a procesos de envejecimiento y deterioro. Por ello, es fundamental tener en cuenta la resiliencia y los problemas climáticos en la planificación comunitaria, especialmente en el diseño de edificios e infraestructuras civiles.
El impacto de eventos extremos compuestos (como un tsunami posterior a un terremoto, o marejadas ciclónicas e inundaciones fluviales tras vientos de huracán) también puede intensificarse debido a los efectos climáticos (Bruneau et al., 2017). Actualmente, existe una falta de guías o herramientas suficientes para considerar estos eventos compuestos y su impacto en el entorno construido. Además de predecir peligros futuros, la no estacionariedad de los efectos climáticos en los eventos de peligro requerirá nuevos enfoques para abordar y comunicar la incertidumbre (Cooke, 2015).
El concepto de resiliencia se basa en la funcionalidad, que puede medirse a nivel de edificios, sistemas de infraestructura o comunidades. Por ello, los análisis de resiliencia deben adaptarse a la escala evaluada y utilizar métodos claros para agregar y desagregar información entre diferentes escalas. Las múltiples escalas de análisis de resiliencia también tienen implicaciones para las proyecciones climáticas regionales, en las que pueden ser necesarias proyecciones correlacionadas en lugares específicos.
Los edificios y los sistemas de infraestructura civil se diseñan y mantienen según diversas regulaciones, códigos y mejores prácticas, cada uno con su propia base de diseño y fiabilidad para evaluar el rendimiento (McAllister et al., 2022). Cada sistema tiene distintos objetivos de rendimiento, como la seguridad en edificios frente a eventos poco frecuentes o la interrupción en los servicios de electricidad y agua ante eventos frecuentes. La falta de coordinación genera disparidades en el rendimiento del entorno construido ante un mismo evento de peligro, que aumentan aún más al considerar el desempeño en términos de recuperación. Aunque la fiabilidad mide si se logran los objetivos de rendimiento, se requieren métricas diferentes para evaluar la recuperación de la funcionalidad.
En algunos sistemas, la fase de recuperación se mide en horas (por ejemplo, en los sistemas de distribución eléctrica), mientras que en otros puede medirse en meses (por ejemplo, en la reparación de un puente o túnel dañado). Estas disparidades se identifican y abordan mejor con una evaluación a nivel comunitario que permita identificar las necesidades específicas de cada proyecto. Una herramienta comúnmente utilizada es la denominada tabla de resiliencia, introducida por primera vez en San Francisco (Poland, 2009). En estas tablas, la comunidad establece el tiempo deseado para alcanzar un conjunto de métricas de desempeño de diversas infraestructuras (por ejemplo, el 75 % de las carreteras funcionales en 3 meses). Estas metas se comparan con el tiempo de recuperación previsto, evaluado por expertos técnicos. Los sectores donde la discrepancia entre la recuperación deseada y la prevista es mayor son aquellos donde más se necesitan intervenciones.
Tabla 1. Plazos para los objetivos de reconstrucción en un seísmo (Poland, 2009).
| Fase | Marco temporal | Condición del entorno construido |
| 1 | 1 a 7 días | Respuesta inicial y preparación para la reconstrucción |
| Inmediato | El alcalde ha declarado una emergencia local y ha abierto el Centro de Operaciones de Emergencia. Los hospitales, las comisarías, los parques de bomberos y los centros de operaciones de los departamentos de la ciudad están operativos. | |
| Dentro de 4 horas | Las personas que salgan o regresen a la ciudad para llegar a sus hogares pueden hacerlo | |
| Dentro de 24 horas | Los trabajadores de respuesta a emergencias pueden activarse y sus operaciones están completamente operativas. Los hoteles designados para alojar a estos trabajadores son seguros y están operativos. Los refugios están abiertos. Todos los hogares ocupados son inspeccionados por sus ocupantes y menos del 5 % de las viviendas son consideradas inseguras para ser ocupadas. Los residentes se refugiarán en edificios con daños superficiales, aunque los servicios públicos no funcionen. | |
| Dentro de 72 horas | El 90 % de los sistemas de servicios públicos (energía, agua, aguas residuales y comunicación) están operativos y prestan apoyo a las instalaciones de emergencia y a los vecindarios. Asimismo, el 90 % de las principales rutas de transporte, incluidos los cruces de la bahía y los aeropuertos, están abiertos al menos para la respuesta a emergencias. Los esfuerzos de recuperación inicial y reconstrucción se centrarán en reparar viviendas, escuelas y oficinas de proveedores médicos para que puedan utilizarse, además de restablecer los servicios públicos necesarios. Los servicios esenciales de la ciudad están completamente restablecidos. | |
| 2 | 30 a 60 días | Viviendas restauradas – necesidades sociales continuas cubiertas |
| Dentro de 30 días | Todos los sistemas de servicios públicos y las rutas de transporte que atienden a los vecindarios han recuperado el 95 % de los niveles de servicio previos al evento. El transporte público funciona al 90 % de su capacidad. Las escuelas públicas están abiertas y en funcionamiento. El 90 % de los negocios del barrio están abiertos y atendiendo a la fuerza laboral. | |
| Dentro de 60 días | Los aeropuertos están operativos y se pueden utilizar con normalidad. El transporte público funciona al 95 % de su capacidad. Las rutas de transporte menores se están reparando y reabriendo. | |
| 3 | Varios años | Reconstrucción a largo plazo |
| Dentro de 4 meses | Los refugios temporales se han cerrado. Todos los hogares desplazados han regresado a sus hogares o han sido reubicados de forma permanente. El 95 % de los servicios minoristas de la comunidad han reabierto. El 50 % de los negocios de apoyo que no forman parte de la fuerza laboral están reabiertos. | |
| Dentro de 3 años | Todas las operaciones comerciales, incluidos todos los servicios de la ciudad que no estén relacionados con la respuesta a emergencias o la reconstrucción, se han restablecido a los niveles previos al seísmo. |
Esta herramienta sencilla se utiliza para representar posibles efectos de los riesgos en un conjunto de escenarios posibles. Actualmente, estos se identifican para cada comunidad en función de los riesgos previstos y de las directrices disponibles. Los efectos del cambio climático pueden incorporarse seleccionando un conjunto de escenarios de eventos extremos que representen el clima futuro. Para avanzar en los análisis y resultados de resiliencia, es necesario un enfoque estandarizado para identificar estos escenarios de riesgo.
Los edificios, puentes y otras infraestructuras tienden a diseñarse para vidas útiles de entre 50 y 100 años. Sin embargo, muchos edificios e infraestructuras se utilizan más allá de su vida útil y su desempeño depende de rehabilitaciones, actualizaciones y mantenimiento. Por lo tanto, la vida útil de edificios, puentes y otras infraestructuras abarca un período en el que el clima puede cambiar sustancialmente, por lo que dichos sistemas se ven expuestos a condiciones y acciones climáticas diferentes a las especificadas en su proyecto. Esta misma consideración se aplica a las evaluaciones de resiliencia.
Todo el proceso de evaluación de la resiliencia comunitaria, desde la selección de peligros hasta la evaluación de escenarios y las evaluaciones cuantitativas del rendimiento, debe tener en cuenta la no estacionariedad de los efectos climáticos. Al evaluar el impacto del cambio climático en el diseño, el mantenimiento y la remodelación, la propiedad desempeña un papel crucial. Cuando los edificios e infraestructuras tienen el mismo propietario durante su vida útil, hay incentivos más fuertes para incluir consideraciones de resiliencia y cambio climático en la planificación y el mantenimiento. En cambio, los sistemas diseñados y mantenidos por diferentes entidades suelen cumplir solo con los requisitos mínimos, a menos que la demanda de resiliencia, consideraciones climáticas o mejoras que se puedan trasladar a los usuarios sea clara.
Las dependencias e interdependencias entre los sistemas de infraestructura de una comunidad requieren la coordinación de múltiples propietarios, lo que puede resultar difícil. Mejorar la resiliencia de un sistema frente a los efectos climáticos futuros puede ser menos efectivo de lo planeado si los propietarios o administradores de los sistemas de infraestructura interdependientes no realizan mejoras similares.
Desempeño funcional del entorno construido
Los objetivos de desempeño comunitario suelen expresarse como aspiraciones a largo plazo para la funcionalidad de los sistemas físicos, sociales y económicos. La incorporación del cambio climático en la funcionalidad a largo plazo de los sistemas comunitarios debe abordarse urgentemente. Los proyectistas necesitan objetivos cuantitativos de desempeño y criterios de diseño para evaluar instalaciones y sistemas individuales que puedan apoyar los objetivos comunitarios y hacer frente a la considerable incertidumbre asociada al cambio climático y a los eventos futuros.
Un entorno construido con un desempeño aceptable es necesario, pero no suficiente, para establecer la resiliencia comunitaria. Esta resiliencia abarca metas sociales y económicas, así como objetivos relacionados con los servicios físicos. Para vincular la respuesta de los sistemas de infraestructura a los objetivos de resiliencia, es fundamental cuantificar su rendimiento colectivo mediante métricas de funcionalidad y recuperación. Desarrollar métricas que respalden los objetivos sociales es crucial para abordar la resiliencia comunitaria a nivel nacional. A continuación, se muestran algunos ejemplos de metas y métricas de resiliencia comunitaria en la Tabla 2. Las métricas de resiliencia para los servicios de infraestructura son más relevantes para los ingenieros estructurales, pero el rendimiento resiliente del entorno construido también contribuye a los objetivos sociales y económicos. Por lo tanto, estos objetivos deben tenerse en cuenta al evaluar soluciones para el diseño, el mantenimiento o las mejoras estructurales.
Tabla 2. Ejemplos de metas de desempeño comunitario y métricas de resiliencia
| Metas de rendimiento comunitario | Ejemplos de métricas de resiliencia |
|---|---|
| Estabilidad poblacional | Desplazamiento y migración; disponibilidad de viviendas. |
| Estabilidad económica | Cambio en el empleo, impuestos e ingresos (recursos), presupuesto comunitario (necesidades). |
| Estabilidad de servicios sociales | Acceso a atención médica, educación, comercio minorista, banca. |
| Estabilidad de servicios físicos | Funcionalidad de edificios, transporte, agua, aguas residuales, energía eléctrica, gas, comunicaciones. |
| Estabilidad gubernamental | Acceso a protección policial y contra incendios; servicios gubernamentales públicos esenciales. |
Fuente: Ellingwood et al. (2020).
La recuperación funcional se refiere al restablecimiento de las funciones básicas del edificio o sistema de infraestructura tras un evento adverso. Desde la perspectiva de la resiliencia, el diseño de estos sistemas debe tener en cuenta el daño potencial y la forma en que se recuperarán durante el proceso de diseño. Este aspecto se aborda en parte en instalaciones críticas como hospitales y refugios, donde se aumentan los requisitos de carga y deformación para construir estructuras más sólidas.
Desde la perspectiva de la resiliencia comunitaria, otros edificios también pueden considerarse críticos según su función, como residencias de personas mayores y escuelas. Sin embargo, los códigos actuales se centran en la seguridad de las personas en edificios e infraestructuras individuales, sin considerar explícitamente las formas de fallo ni las reparaciones necesarias para restaurar la funcionalidad en un tiempo determinado. Para establecer normas que incluyan objetivos de desempeño en términos de funcionalidad y resiliencia, además de la seguridad, será necesario cambiar el proceso regulatorio, pasando de un diseño basado en componentes a un enfoque sistémico.
Se necesitan orientaciones sobre mejores prácticas y criterios de proyecto con objetivos que respalden las metas de resiliencia comunitaria para incluir la recuperación funcional. Se requieren objetivos funcionales y criterios para abordar mejor el papel de las infraestructuras, incluidos los niveles esperados de daño, el impacto en la funcionalidad de los edificios y otras infraestructuras, las reparaciones necesarias para restablecer la funcionalidad e impactos potenciales en la recuperación social y económica de la comunidad.
A medida que la ingeniería se esfuerza por incorporar los conceptos de resiliencia y recuperación funcional en su práctica, es necesario abordar el cambio climático en paralelo. La ASCE (2015) destacó un dilema clave para los ingenieros en ejercicio: «Aunque la comunidad científica está de acuerdo en que el clima está cambiando, existe una incertidumbre significativa sobre las distribuciones espaciales y temporales de los cambios durante la vida útil de los diseños y planes de infraestructura. La necesidad de que la infraestructura de ingeniería satisfaga las necesidades futuras y la incertidumbre sobre el clima futuro plantean un dilema para los ingenieros».
Los cambios en las condiciones climáticas pueden afectar a las infraestructuras y a su resiliencia de diversas maneras. ASCE (2018) identificó los tipos de impactos relacionados con el clima que deben abordarse, en particular, los relacionados con las inundaciones (el aumento de los niveles, de las velocidades de flujo y de las alturas de las olas), con las precipitaciones (las acciones de lluvia y nieve en los techos y el aumento de las acciones de las heladas en las estructuras) y con el viento (la mayor intensidad y frecuencia de tormentas y huracanes). El Manual de Práctica 144 de ASCE (ASCE, 2021) utiliza métodos probabilísticos para el análisis y la gestión de riesgos en los proyectos para abordar las incertidumbres dentro de un horizonte temporal. Este enfoque incluye la identificación y el análisis de riesgos, fallos del sistema, probabilidades asociadas y consecuencias, incluyendo pérdidas directas e indirectas, cuantificación de fallos y recuperación para la resiliencia, efectos en las comunidades, la economía de la resiliencia y las tecnologías para mejorar la resiliencia tanto en infraestructuras nuevas como existentes.
La resiliencia incorpora la dimensión temporal a través del proceso de recuperación y reconstrucción, pero los modelos de recuperación aún se encuentran en una etapa inicial de desarrollo. Además, durante la recuperación es necesario tener en cuenta las interdependencias, por ejemplo, cuando un edificio o sistema es funcional, pero otro sistema del que depende (por ejemplo, servicios públicos) aún no puede proporcionar el servicio necesario.
Cuando los edificios no son funcionales debido a retrasos en la financiación de reparaciones u otras causas, los efectos son enormes. En efecto, los retrasos en la recuperación de la funcionalidad de los edificios afectan directamente a la población, que se ve obligada a desplazarse y aumenta la probabilidad de emigrar, lo que repercute negativamente en las métricas de estabilidad poblacional (Tabla 2). La emigración también depende de la cohesión social y de factores como la fuente de refugio, empleo y educación de los niños en un hogar.
Desafíos para la resiliencia comunitaria en un clima cambiante
En la próxima década, probablemente evolucionen las mejores prácticas de los profesionales del diseño y las decisiones de los planificadores urbanos y las autoridades reguladoras para apoyar la forma en que se aborda el cambio climático en lo que respecta a la resiliencia comunitaria. El Diseño Basado en el Desempeño (PBD) ofrece una forma de abordar este conflicto y resolver los desafíos inherentes que surgirán al atender tanto las necesidades de las instalaciones como las de la comunidad. Desarrollar e incorporar enfoques PBD que aborden los peligros e impactos del cambio climático en las mejores prácticas, estándares y códigos es una necesidad urgente para la profesión de la ingeniería y la sociedad.
Los desafíos para los ingenieros estructurales incluyen los siguientes (Ellingwood et al., 2020):
- Identificación de metas comunes de resiliencia comunitaria que aborden los futuros impactos del cambio climático, las cuales deberían ser establecidas por un grupo amplio de partes interesadas.
- Objetivos de desempeño para los edificios, según categorías funcionales o agrupaciones (por ejemplo, edificios residenciales, instalaciones comerciales, gubernamentales) o instituciones socioeconómicas (por ejemplo, educación, atención médica), deben expresarse como requisitos compatibles con la práctica de ingeniería y ser prácticos de implementar desde una perspectiva de ingeniería.
- Objetivos de fiabilidad para los edificios individuales en la práctica de diseño estructural actual (por ejemplo, ASCE 7-22, Sección 1.3) identifican requisitos mínimos de rendimiento a nivel de componente para la mayoría de las acciones, excepto las sísmicas. Se necesitan fiabilidades objetivo y criterios de desempeño a nivel de sistema para todas las cargas, con el fin de apoyar las metas de resiliencia comunitaria.
- Códigos, normas y regulaciones para los sistemas de infraestructura (por ejemplo, edificios, puentes, comunicaciones críticas) deben coordinarse para apoyar las metas de resiliencia comunitaria e impactos del cambio climático, y para abordar la funcionalidad y recuperación de la infraestructura civil, así como la seguridad de las personas.
En resumen, la resiliencia comunitaria se refiere a la capacidad de las comunidades para adaptarse a situaciones adversas, mantener sus funciones esenciales y recuperarse rápidamente después de eventos extremos. Para desarrollar estrategias de adaptación eficaces, especialmente frente al cambio climático, es crucial que los miembros de la comunidad participen activamente en la identificación de sus valores y prioridades. Las comunidades vulnerables suelen sufrir impactos desproporcionados debido a factores socioeconómicos y demográficos, lo que subraya la necesidad de enfoques equitativos en la planificación de la resiliencia. Además, es fundamental tener en cuenta las interdependencias entre los sistemas de infraestructura y la coordinación entre múltiples propietarios para mejorar la resiliencia. La planificación debe incluir objetivos de rendimiento claros y métricas que aborden tanto la funcionalidad como la recuperación de los sistemas, para que las comunidades puedan hacer frente a los desafíos climáticos futuros de manera efectiva.
Aquí tenéis un mapa mental sobre el contenido de las reflexiones anteriores, que espero, os sea útil.
Dejo a continuación un documento que creo que os puede interesar sobre este tema.
Referencias:
ASCE. (2015). Adapting infrastructure and civil engineering practice to a changing climate. Reston, VA: ASCE.
ASCE. (2018). Climate-resilient infrastructure: Adaptive design and risk management, MOP 140. Reston, VA: ASCE.
ASCE. (2021). Hazard-resilient infrastructures: Analysis and design, MOP 144. Reston, VA: ASCE.
Bruneau, M., Barbato, M., Padgett, J. E., Zaghi, A. E., et al. (2017). State-of-the-art on multihazard design. Journal of Structural Engineering, 143(10), 03117002.
Cooke, R. M. (2015). Messaging climate change uncertainty. Nature Climate Change, 5(1), 8–10.
Ellingwood, B. R., van de Lindt, J. W., & McAllister, T. (2020). Community resilience: A new challenge to the practice of structural engineering. Structural Magazine, 27(11), 28–30.
Ellingwood, B. R., Bocchini, P., Lounis, Z., Ghosn, M., Liu, M., Yang, D., Capacci, L., Diniz, S., Lin, N., Tsiatas, G., Biondini, F., de Lindt, J., Frangopol, D.M., Akiyama, M., Li, Y., Barbato, M., Hong, H., McAllister, T., Tsampras, G. & Vahedifard, F. (2024). Impact of Climate Change on Infrastructure Performance. In Effects of Climate Change on Life-Cycle Performance of Structures and Infrastructure Systems: Safety, Reliability, and Risk (pp. 115-206). Reston, VA: American Society of Civil Engineers.
Eisenhauer, E., Henson, S., Matsler, A., Maxwell, K., Reilly, I., Shacklette, M., Julius, S., Kiessling, B., Fry, M., Nee, R., Bryant, J., Finley, J., & Kieber, B. (2024). Centering equity in community resilience planning: Lessons from case studies. Natural Hazards Forum, Washington, D.C.
IPCC (1997). The regional impacts of climate change: an assessment of vulnerability. IPCC, Geneva.
McAllister, T., Walker, R., & Baker, A. (2022). Assessment of resilience in codes, standards, regulations, and best practices for buildings and infrastructure systems. NIST Technical Note 2209. National Institute of Standards and Technology. https://doi.org/10.6028/NIST.TN.2209
O’Neill, B., van Aalst, M., Zaiton Ibrahim, Z., Berrang Ford, L., Bhadwal, S., Buhaug, H., Diaz, D., Frieler, K., Garschagen, M., Magnan, A., Midgley, G., Mirzabaev, A., Thomas, A., & Warren, R. (2022). Key risks across sectors and regions. In H.-O. Pörtner, D. C. Roberts, M. Tignor, E. S. Poloczanska, K. Mintenbeck, A. Alegría, M. Craig, S. Langsdorf, S. Löschke, V. Möller, A. Okem, & B. Rama (Eds.), Climate change 2022: Impacts, adaptation and vulnerability. Contribution of Working Group II to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change (pp. 2411–2538). Cambridge University Press. https://doi.org/10.1017/9781009325844.025
Poland, C. D. (2009). The resilient city: Defining what San Francisco needs from its seismic mitigation policies. San Francisco Planning and Urban Research Association Report. Earthquake Engineering Research Institute.
Vogel, J., Carney, K. M., Smith, J. B., Herrick, C., et al. (2016). Climate adaptation: The state of practice in US communities. The Kresge Foundation and Abt Associates.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.