Mes: septiembre 2020

“The asset time bomb”: La bomba de relojería de las infraestructuras, y en particular, de los puentes

Figura 1. Colapso del puente I-35W en Minneapolis. https://thestartupgrowth.com/2019/02/21/structural-health-monitoring-market-driven-by-rapid-expansion-in-the-infrastructure-sector-till-2024/

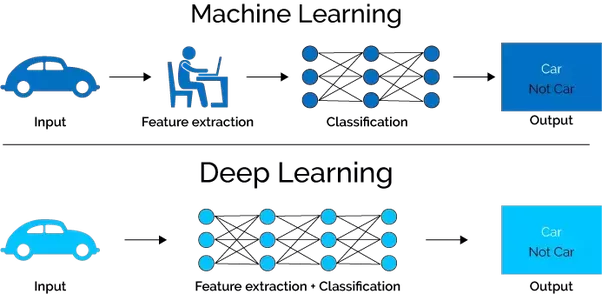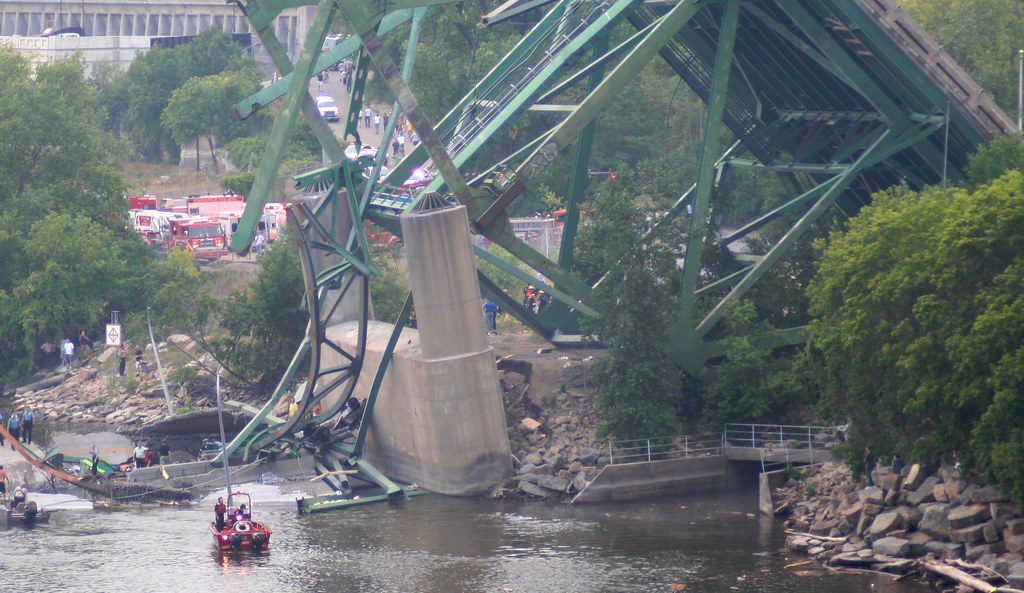
Una noticia aparecida el 9 de diciembre de 2018 en El País con el siguiente titular “Fomento admite que hay 66 puentes con graves problemas de seguridad” abrió cierta inquietud en la opinión pública sobre la seguridad de nuestros puentes. Esta inquietud irrumpió en agosto de ese mismo año con el derrumbe de un puente en Génova (Italia). Pero los ejemplos no quedan aquí. Podríamos hablar de la sustitución de los cables del puente Fernando Reig, en Alcoy, o del Puente del Centenario, en Sevilla. O del derribo del puente Joaquín Costa, en Madrid. Ejemplos tenemos en todo el mundo. En cualquier caso, estamos hablando de cifras millonarias, de cortes de tráfico, pérdidas humanas, por poner algunas consecuencias sobre la mesa.

Los puentes son componentes críticos de las infraestructuras, pues su correcto funcionamiento es básico para la resiliencia de nuestros entornos urbanos. Sin embargo, un gran número de infraestructuras que están llegando al final de su vida útil al mismo tiempo. De hecho, la vida útil de muchos puentes se espera que sea menor a la proyectada debido al continuo deterioro provocado por el incremento del tráfico y de los impactos ambientales. Esto constituye una auténtica bomba de relojería (Thurlby, 2013), que junto al reto de la reducción de los impactos ambientales, son razones más que suficientes para preocuparnos de mejorar el mantenimiento de nuestros puentes. De hecho, ya hemos comentado en un artículo anterior un concepto totalmente relacionado con éste: la “crisis de las infraestructuras“. Yo me atrevería a afirmar algo que puede parecer muy duro: el derrumbe de nuestra civilización será paralelo al de las infraestructuras que les da soporte.

Hoy día los gestores de las infraestructuras tienen ante sí un reto importante consistente en mantenerlas en un estado aceptable con presupuestos muy limitados. De hecho, la inspección de los puentes, su mantenimiento y reparación constituyen tareas rutinarias necesarias para mantener dichas infraestructuras en buenas condiciones (Tong et al., 2019). Sin embargo, el problema pasa a ser grave cuando una parte significativa del parque de infraestructuras se encuentra cercano al final de su vida útil. Y lo que aún es peor, cuando existen riesgos de alto impacto y de baja probabilidad que pueden afectar gravemente a las infraestructuras. Resolver este problema es complicado, pues no se presta fácilmente a la exploración con los instrumentos analíticos y de previsión tradicionales.

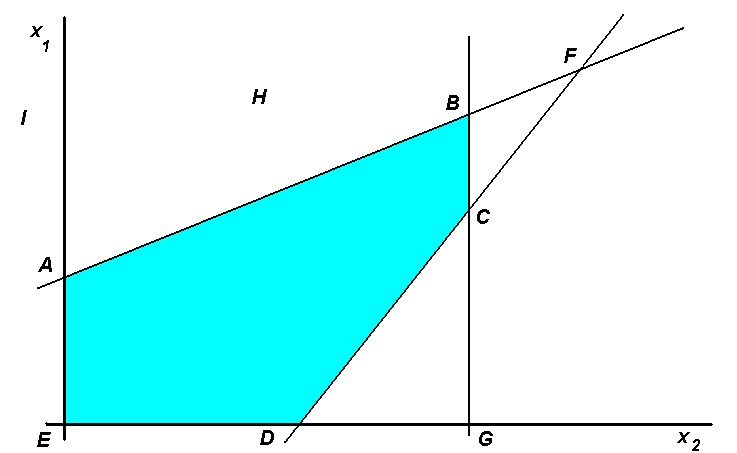
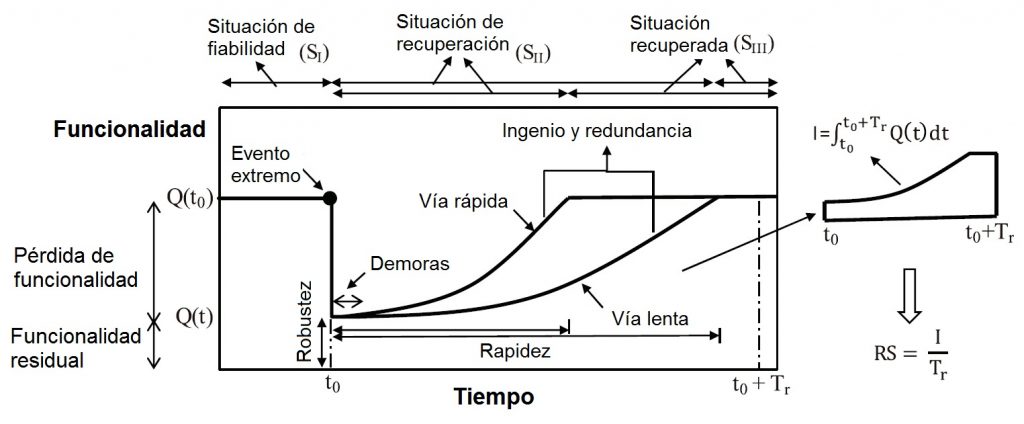
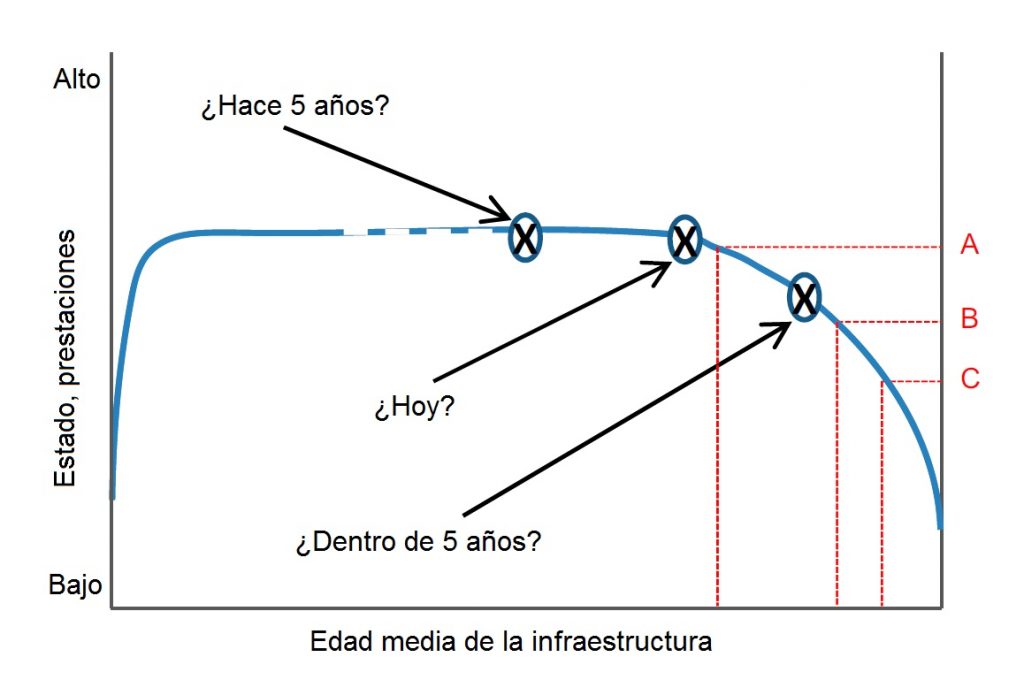
El estado o deterioro de una infraestructura sigue un comportamiento similar, pero invertido, de la llamada “curva de la bañera“, que es una gráfica que representa los fallos durante el periodo de vida útil de un sistema o de una máquina. En este caso, según vemos en la Figura 2, el estado de condición o las prestaciones de la infraestructura permanece alto durante un periodo de tiempo hasta que empieza a decaer. Para los gestores es necesario conocer el comportamiento de las infraestructuras para tomar decisiones. Sin embargo, muchas veces desconocen en qué posición de la curva se encuentran y, lo que es peor, a qué ritmo se va a deteriorar. Por ejemplo, en la Figura 2 podemos ver que la caída en las prestaciones de A a B, o de B a C son similares, pero la velocidad de deterioro es muy diferente. Y lo que es peor de todo, llega un momento que la caída en las prestaciones ocurre de forma muy acelerada, sin capacidad de reacción por parte de los gestores. Por eso se ha utilizado el símil de la “bomba de relojería”.

Figura 2. Estado o prestaciones de una infraestructura (Thurlby, 2013)

La gestión y el mantenimiento de los puentes está empezando a ser un problema de una magnitud que está empezando a ser más que preocupante. Algunos datos son un ejemplo de ello: en el año 2019, 47000 puentes de los puentes en Estados Unidos, (más del 20% del total) presentan deficiencias estructurales (American Road & Transportation Builders Association, 2019); en Reino Unido, más de 3000 puentes estaban por debajo de los estándares y requerían reparación (RAC Foundation, 2019). Estos son buenos argumentos para aumentar la vida útil de los puentes.

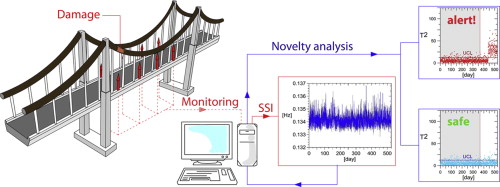
Una de las tecnologías para mejorar la gestión y el mantenimiento de los puentes es la vigilancia de su estado estructural (structural health monitoring, SHM), que trata de mejorar el comportamiento de la estructura mediante el aprendizaje de los datos obtenidos durante su vida útil mediante su monitorización (Figura 3). Estos datos sirven para actualizar los modelos y comprobar el estado en que se encuentra la estructura, lo cual permite minimizar la incertidumbre de los parámetros empleados en los modelos. Sin embargo, aún no se ha resuelto completamente el paso de la obtención de los datos del puente en tiempo real a la toma de decisiones en la gestión y mantenimiento de los puentes.

Figura 3. Structural health monitoring. https://thestartupgrowth.com/2019/02/21/structural-health-monitoring-market-driven-by-rapid-expansion-in-the-infrastructure-sector-till-2024/

En un artículo anterior se explicó el concepto de gemelos digitales (digital twins). Estos modelos actualizados constantemente mediante la monitorización del puente, permitirían conocer en tiempo real el estado estructural del puente y también predecir su comportamiento en el caso de que ocurrieran determinadas circunstancias. Esta información sería clave a la hora de tomar decisiones en la gestión y el mantenimiento del puente.

Las preguntas clave que deberíamos responder serían las siguientes: ¿Es el puente seguro?, ¿cuánto tiempo será el puente seguro?, ¿cuál es el comportamiento estructural actual del puente?, ¿cuándo y cómo deberemos intervenir en el puente?

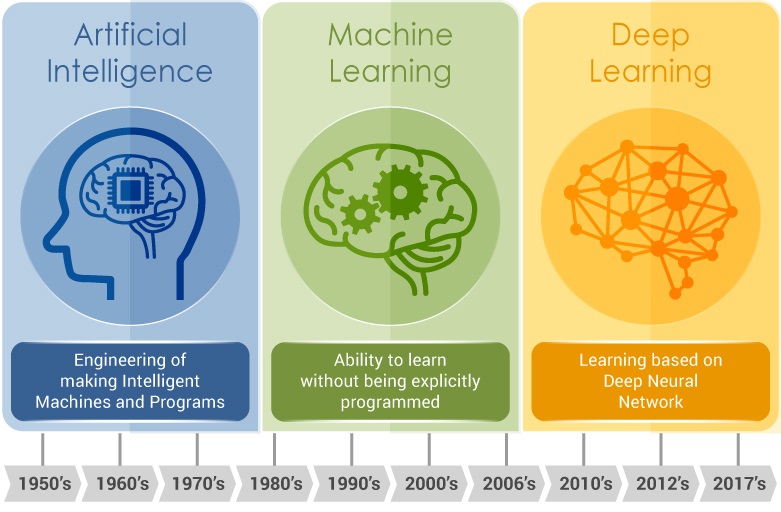
La respuesta a estas preguntas no es tan evidente como pudiera parecer a simple vista. Los gestores de las infraestructuras deberían ser capaces de entender y valorar en su justa medida los resultados estructurales de los modelos cuyos datos se actualizan en tiempo real. La dificultad estriba en conocer no solo los datos, sino las causas subyacentes a los cambios en el comportamiento estructural. Una ayuda son las técnicas procedentes de la inteligencia artificial, como el aprendizaje profundo, que permiten interpretar ingentes cantidades de datos e identificar patrones y correlaciones entre dichos datos. En un artículo anterior hablamos de este tema. Por otra parte, la actualización de los datos procedentes de la vigilancia de los puentes debería ser automática y en tiempo real. Aquí vuelve a cobrar importancia la inteligencia artificial, aunque nunca debería suplantar el conocimiento ingenieril que permite interpretar los resultados proporcionados por los algoritmos.

Por otra parte, la modelización del riesgo y la resiliencia es una labor necesaria para entender la vulnerabilidad de las infraestructuras. De esta forma seríamos capaces de desarrollar estrategias de mitigación, que podrían ser complementarias a las estrategias de gestión del deterioro que se han explicado anteriormente.

Por tanto, existe un auténtico salto entre la investigación dedicada a la monitorización en tiempo real de los puentes y la toma de decisiones para su gestión y mantenimiento. Los gemelos digitales apoyados en los actuales desarrollos tecnológicos como el “Internet de las cosas“, deberían permitir el paso de la investigación y el desarrollo a la innovación directamente aplicable a la realidad de la gestión de las infraestructuras.

Referencias:

AMERICAN ROAD & TRANSPORTATION BUILDERS ASSOCIATION (2019). 2019 Bridge Report. https://artbabridgereport.org/

RAC Foundation. (2019). Bridge maintenance table – GB local authorities. https://www.racfoundation.org/media-centre/bridge-maintenance-backlog-grows

THURLBY, R. (2013). Managing the asset time bomb: a system dynamics approach. Proceedings of the Institution of Civil Engineers – Forensic Engineering, 166(3):134-142.

TONG, X.; YANG, H.; WANG, L.; MIAO, Y. (2019). The development and field evaluation of an IoT system of low-power vibration for bridge health monitoring, Sensors 19(5):1222.

YEPES, V. (2020). Computación cuántica y gemelos híbridos digitales en ingeniería civil y edificación. https://victoryepes.blogs.upv.es/2019/10/30/computacion-cuantica-gemelos-digitales/

YEPES, V. (2020). La inteligencia artificial en la ingeniería civil. https://victoryepes.blogs.upv.es/2020/09/08/la-inteligencia-artificial-en-la-ingenieria-civil/

YEPES, V. (2020). El aprendizaje profundo (deep learning) en la optimización de estructuras. https://victoryepes.blogs.upv.es/2020/09/15/el-aprendizaje-profundo-deep-learning-en-la-optimizacion-de-estructuras/

YEPES, V. (2020). La resiliencia de las infraestructuras. https://victoryepes.blogs.upv.es/2020/09/17/la-resiliencia-de-las-infraestructuras/

Licencia de Creative Commons
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Programación lineal con Matlab

Los problemas de programación lineal consisten en optimizar una ecuación lineal que está sujeta a una serie de restricciones conformadas por desigualdades lineales. Para resolverlos el toolbox de Matlab posee la función linprog, la cual posee tres algoritmos para su solución, el método de larga escala, el método simplex y el de Active Set.

La sintaxis para llamar esta función es la siguiente:

x = linprog (f ,A, b, Aeq, beq, lb, ub, x0, options)

Donde:

f: es el vector de coeficientes de la función objetivo, organizado según las variables (Matlab intentará minimizar siempre, por tanto multiplicaremos por -1 si queremos maximizar)

A, b: corresponden a las restricciones de desigualdad, siendo el primero la matriz y el segundo el vector del lado derecho del sistema de inecuaciones Ax<=b.

Aeq, beq: tienen el mismo tratamiento que A y b, respectivamente, teniendo en cuenta que los nuevos corresponden a un sistema de ecuaciones, en tanto que los antiguos constituían uno de inecuaciones.

lb, ub: son, respectivamente, los límites inferior y superior de la región donde se espera que se encuentre el punto óptimo.

x0: es el punto inicial para la iteración. Según el algoritmo usado, es posible, o no, omitir este último.

Ejercicio 1:

Un taller confecciona cuatro productos: F, B, V y A para los que utiliza 2 horas, 3 horas y media, 4 horas y media y 5 horas de máquina y 1, 2, 1 y 10 horas de mano de operario para cada producto, respectivamente. Si se dispone de 3000 horas de máquina y 2000 horas de operario, y sabiendo que los beneficios obtenidos por unidad son de 6, 10, 13 y 30 u.m,  respectivamente, calcular el número de productos de cada tipo que deben producirse para obtener el máximo beneficio.

El planteamiento para el primer problema es:

Maximizar: 6×1 + 10×2 + 13×3 + 30×4
Sujeto a: 2×1 + 3,5×2 + 4,5×3 + 5×4 = 3000
x1 + 2×2 + x3 + 10×4 = 2000
x1, x2, x3, x4 ≥ 0

Para definir todas las variables del primer problema, en Matlab, se debe escribir:
>> f = [-6 -10 -13 -30];
>> A = -eye(4); % matriz identidad de tamaño 4×4
>> b = [0 0 0 0];
>> Aeq = [2 3.5 4.5 5 ; 1 2 1 10];
>> beq = [3000 2000];

Finalmente, se usa la sintaxis respectiva con las variables del primer problema, cargadas previamente, para obtener lo siguiente:

>> [x,fval] = linprog(f,A,b,Aeq,beq,lb,ub,x0)
Optimization Terminated.

x =
0.0000
0.0000
500.0000
150.0000
fval =
-1.1000e+004

Ejercicio 2:

Una empresa que se dedica a la producción de frascos de perfume, de agua de colonia y de champú utiliza tres factores productivos F1, F2 y F3 disponiendo de 240, 460 y 430 unidades, respectivamente. Las cantidades de dichos factores utilizados en la producción de un frasco por cada producto se detallan en la siguiente tabla:

Cuadro
La formulación el segundo problema es:Sabiendo que el precio unitario de venta del perfume es de 5 unidades monetarias, el del agua de colonia de 2 y el del champú de 3, y que se vende todo lo que se produce, calcular el beneficio máximo y el número de frascos de cada tipo que debe producir la empresa para obtenerlo.

Maximizar: 5×1 + 2×2 + 3×3
Sujeto a: F1 ≤ 240
F2 ≤ 460
F3 ≤ 430

La asignación de los valores de las variables, correspondientes al segundo problema, se realiza de la siguiente manera:

>> f = [-5 -2 -3];
>> A = [1 2 1 ; 2 0 3 ; 0 4 1];
>> b = [240 460 430];
>> x0 = [0 0 0];

>> [x,fval] = linprog(f,A,b,[],[],[0 0 0])
Optimization Terminated.
x =
230.0000
5.0000
0.0000
fval =
-1.1600e+003

Os dejo a continuación algunos problemas que, seguro, podréis abordar con Matlab:

Descargar (PDF, 164KB)

Referencia:

Cabezas, I.; Páez, J.D. (2010). Matlab. Toolbox de optimización. Aplicaciones en ciencias económicas. Unidad de Informática y Comunicaciones. Facultad de Ciencias Económicas. Universidad Nacional de Colombia, Bogotá D.C. (enlace).

Mejorando la I+D+i mediante la normalización y la certificación: el caso del sector de la construcción español

Figura. Calidad, innovación y gestión del conocimiento (Pellicer et al., 2008)

El grado de desarrollo de una comunidad se mide, a menudo, por su inversión en investigación, desarrollo e innovación (I+D+i). Los países industrializados asumen la necesidad de investigar nuevas técnicas, materiales y procesos con objeto de alcanzar una mayor eficiencia y sustentabilidad en cada tarea productiva. La normalización y la certificación de la gestión de proyectos o sistemas de I+D+i supone una herramienta adecuada para optimizar los resultados, sobre todo cuando es una política internacional el incentivo de las tareas de I+D+i. Las empresas buscan acreditar ante la administración pública los recursos destinados a la I+D+i, obteniendo ventajas fiscales a lo largo de todo el proceso. A pesar de que el sector de la construcción es importante en todas las economías desarrolladas y en vías de desarrollo, las empresas constructoras invierten poco en I+D+i comparativamente con otros sectores. La relación entre la normalización y la innovación sigue siendo una asignatura pendiente dentro del campo de la gestión de la construcción. A lo largo del presente artículo se analiza la situación internacional en materia de normalización y certificación de actividades de I+D+i, señalando el carácter innovador de las normas españolas UNE 166000. Se exponen los resultados de un estudio sistemático destinado a conocer la situación actual en el sector de la construcción en España, referente a la normalización y a la certificación. Esta nueva familia de normas podría servir como referente para otros países, siempre funcionando conjuntamente con las series de normas ISO 9000 y 14000.

Palabras clave: Innovación, certificación, construcción, normalización, gestión

Referencia:

PELLICER E., YEPES V., CORREA C.L.; MARTÍNEZ, G. (2008). Enhancing R&D&i through standardization and certification: the case of the Spanish construction industry, Revista Ingeniería de Construcción, 23(2): 112-121.

Descargar (PDF, 768KB)

 

 

Procedimientos de construcción de cimentaciones y estructuras de contención. Segunda edición ampliada

Os presento la segunda edición ampliada del libro que he publicado sobre procedimientos de construcción de cimentaciones y estructuras de contención. El libro trata de los aspectos relacionados con los procedimientos constructivos, maquinaria y equipos auxiliares empleados en la construcción de cimentaciones superficiales, cimentaciones profundas, pilotes, cajones, estructuras de contención de tierras, muros, pantallas de hormigón, anclajes, entibaciones y tablestacas. Pero se ha ampliado esta edición con tres capítulos nuevos dedicados a los procedimientos de contención y control de las aguas subterráneas. Además, de incluir la bibliografía para ampliar conocimientos, se incluyen cuestiones de autoevaluación con respuestas y un tesauro para el aprendizaje de los conceptos más importantes de estos temas. Este texto tiene como objetivo apoyar los contenidos lectivos de los programas de los estudios de grado relacionados con la ingeniería civil, la edificación y las obras públicas.

Este libro lo podéis conseguir en la propia Universitat Politècnica de València o bien directamente por internet en esta dirección: https://www.lalibreria.upv.es/portalEd/UpvGEStore/products/p_328-9-2

El libro tiene 480 páginas, 439 figuras y fotografías, así como 430 cuestiones de autoevaluación resueltas. Los contenidos de esta publicación han sido evaluados mediante el sistema doble ciego, siguiendo el procedimiento que se recoge en: http://www.upv.es/entidades/AEUPV/info/891747normalc.html

Sobre el autor: Víctor Yepes Piqueras. Doctor Ingeniero de Caminos, Canales y Puertos. Catedrático de Universidad del Departamento de Ingeniería de la Construcción y Proyectos de Ingeniería Civil de la Universitat Politècnica de València. Número 1 de su promoción, ha desarrollado su vida profesional en empresas constructoras, en el sector público y en el ámbito universitario. Es director académico del Máster Universitario en Ingeniería del Hormigón (acreditado con el sello EUR-ACE®), investigador del Instituto de Ciencia y Tecnología del Hormigón (ICITECH) y profesor visitante en la Pontificia Universidad Católica de Chile. Imparte docencia en asignaturas de grado y posgrado relacionadas con procedimientos de construcción y gestión de obras, calidad e innovación, modelos predictivos y optimización en la ingeniería. Sus líneas de investigación actuales se centran en la optimización multiobjetivo, la sostenibilidad y el análisis de ciclo de vida de puentes y estructuras de hormigón.

Referencia:

YEPES, V. (2020). Procedimientos de construcción de cimentaciones y estructuras de contención. Colección Manual de Referencia, 2ª edición. Editorial Universitat Politècnica de València, 480 pp. Ref. 328. ISBN: 978-84-9048-903-1.

A continuación os paso las primeras páginas del libro, con el índice, para hacerse una idea del contenido desarrollado.

https://gdocu.upv.es/alfresco/service/api/node/content/workspace/SpacesStore/31b0d684-f0a7-4ee7-b8f4-73694e138d5e/TOC_0328_09_02.pdf?guest=true

Descargar (PDF, 476KB)

 

 

Un enfoque multinivel para mejorar la planificación regional resiliente

Hace unos días tuvimos la ocasión de presentar una comunicación en la segunda edición de “International Conference on Innovative Applied Energy (IPC’20), que si bien iba a ser presencial en Cambridge (Reino Unido), al final se tuvo que realizar en línea por culpa de la pandemia. A continuación os dejo la presentación que hicimos y un resumen de la misma. Espero que os sea de interés.

Referencia:

SALAS, J.; YEPES, V. (2020). UPSS, a multi-level framework for improved resilient regional planning. Proceedings of the Second Edition of the International Conference on Innovative Applied Energy (IPC’20), 15-16 September, Cambridge, United Kingdom. ISBN (978-1-912532-18-6).

Descargar (PDF, 144KB)

 

 

 

La resiliencia de las infraestructuras

Figura 1. https://www.un.org/sustainabledevelopment/es/2015/09/infraestructura-innovacion-e-industrias-inclusivas-claves-para-el-desarrollo/

La resiliencia es un concepto que viene del mundo de la psicología y representa la capacidad para adaptarse de forma positiva frente a situaciones adversas. Proviene del latín resilio, “volver atrás, volver de un salto, resaltar, rebotar”. En el campo de la mecánica, la resiliencia sería la capacidad de un material para recuperar su forma inicial después de haber sido deformado por una fuerza. En la ecología, un sistema es resiliente si puede tolerar una perturbación sin colapsar a un estado completamente distinto, controlado por otro conjunto de procesos. En un entorno tecnológico, este término se relaciona con la capacidad de un sistema de soportar y recuperarse ante desastres y perturbaciones. En este artículo vamos a indagar en el concepto de resiliencia de las infraestructuras.

Así, dentro de los objetivos de desarrollo sostenible de Naciones Unidas (Figura 1), encontramos el Objetivo 9: Construir infraestructuras resilientes, provomer la industrialización sostenible y fomentar la innovación. En efecto, las infraestructuras deben hacer frente al crecimiento de la población, pero también a los crecientes peligros físicos (cinéticos) como el terrorismo, o los asociados al clima extremo y los desastres naturales. La frecuencia y gravedad de estos eventos extremos se prevén crecientes, y, por tanto, es más que previsible un aumento en los costes e impacto humano. Además, debido a la cada vez más informatización y digitalización de las infraestructuras, el riesgo de ataques informáticos a las infraestructuras es más que evidente.

La resiliencia puede asociarse con cuatro atributos: robustez, que es la capacidad para resistir un evento extremo sin que el fracaso en la funcionalidad sea completo; rapidez, que sería la capacidad de recuperarse de forma eficiente y efectiva; la redundancia, que sería la reserva de componentes o de sistemas estructurales sustitutivos; y el ingenio, que sería la eficiencia en la identificación de problemas, priorizando soluciones y movilizando recursos para su solución (Bruneau et al., 2003).

Matemáticamente, se puede evaluar la resiliencia integrando la curva de funcionalidad a lo largo del tiempo (ver Figura 2).

donde Q(t) es la funcionalidad; t0 es el momento en el que ocurre el evento extremo y Tr es el horizonte hasta donde se estudia la funcionalidad.

Figura 2. Valoración de la resiliencia tras un evento extremo (Anwar et al., 2019)

En la Figura 2 se pueden observar los tres estados correspondientes con la funcionalidad. En la situación de fiabilidad, la infraestructura se encuentra con la funcionalidad de referencia, previo al evento extremo. La situación de recuperación comienza tras la ocurrencia del evento extremo, con una pérdida de funcionalidad dependiente de la robustez de la infraestructura, y con una recuperación que depende de los esfuerzos realizados en la reparación, que puede ser rápida o lenta en función del ingenio o la creatividad en las soluciones propuestas, así como de la redundancia de los sistemas previstos. Por último, la situación recuperada es la que ocurre cuando la funcionalidad vuelve a ser la de referencia.

Se comprueba en la Figura 2 cómo una infraestructura pasa de una funcionalidad de referencia a una residual tras el evento extremo. Tras el evento, puede darse una demora en la recuperación de la funcionalidad debido a las tareas de inspección, rediseño, financiación, contratación, permisos, etc.). La recuperación completa de la funcionalidad depende de la forma en la que se han abordado las tareas de reparación. Es fácil verificar que la resiliencia se puede calcular integrando la curva de recuperación de la funcionalidad desde la ocurrencia del evento extremo hasta la completa recuperación, dividiendo dicho valor por el tiempo empleado en dicha recuperación.

Este modelo simplificado permite establecer las pautas para mejorar la resiliencia de una infraestructura:

a) Incrementando la robustez de la infraestructura, es decir, maximizar su funcionalidad residual tras un evento extremo.

b) Acelerando las actividades de recuperación de la funcionalidad de la infraestructura.

En ambos casos, es necesario concebir la infraestructura desde el principio con diseños robustos, con sistemas redundantes y con una previsión de las tareas de reparación necesarias.

Con todo, la capacidad de recuperación comprende cuatro dimensiones interrelacionadas: técnica, organizativa, social y económica (Bruneau et al., 2003). La dimensión técnica de la resiliencia se refiere a la capacidad de los sistemas físicos (incluidos los componentes, sus interconexiones e interacciones, y los sistemas enteros) para funcionar a niveles aceptables o deseables cuando están sujetos a los eventos extremos. La dimensión organizativa de la resiliencia se refiere a la capacidad de las organizaciones que gestionan infraestructuras críticas y tienen la responsabilidad de tomar decisiones y adoptar medidas que contribuyan a lograr la resiliencia descrita anteriormente, es decir, que ayuden a lograr una mayor solidez, redundancia, ingenio y rapidez. La dimensión social de la resiliencia consiste en medidas específicamente diseñadas para disminuir los efectos de los eventos extremos por parte de la población debido a la pérdida de infraestructuras críticas. Análogamente, la dimensión económica de la resiliencia se refiere a la capacidad de reducir tanto las pérdidas directas e indirectas de los eventos extremos.

El problema de estas cuatro dimensiones se pueden sumar de forma homogénea, con interrelaciones entre ellas. El reto consiste en cuantificar y medir la resiliencia en todas sus dimensiones, así como sus interrelaciones. Se trata de un problema de investigación de gran trascendencia y complejidad, que afecta al ciclo de vida de las infraestructuras desde el inicio de la planificación (Salas y Yepes, 2020).

Referencias:

ANWAR, G.A.; DONG, Y.; ZHAI, C. (2020). Performance-based probabilistic framework for seismic risk, resilience, and sustainability assessment of reinforced concrete structures. Advances in Structural Engineering, 23(7):1454-1457.

BRUNEAU, M.; CHANG, S.E.; EGUCHI, R.T. et al. (2003). A framework to quantitatively assess and enhance the seismic resilience of communities. Earthquake Spectra 19(4): 733–752.

SALAS, J.; YEPES, V. (2020). Enhancing sustainability and resilience through multi-level infrastructure planning. International Journal of Environmental Research and Public Health, 17(3): 962. DOI:10.3390/ijerph17030962

Licencia de Creative Commons
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

¿Siempre es válida la ley de Darcy?

Figura 1. Esquema de la ley de Darcy

En un artículo anterior, dentro de los conceptos básicos del agua en medio poroso, se definió la ley de Darcy como una ley experimental que define el movimiento de filtración en un medio poroso saturado. Dicha ley dice que la velocidad del fluido en medio poroso es proporcional al gradiente hidráulico a través del coeficiente de permeabilidad.

Dicho coeficiente no es una propiedad intrínseca del suelo y tiene unidades de velocidad. Aquí se ha supuesto un flujo laminar en medio poroso y una velocidad media a través de una sección “macroscópica” de suelo, es decir, la velocidad aparente a lo largo de las líneas de flujo. A esa velocidad se llama velocidad del flujo o velocidad de Darcy.

Sin embargo, ¿estamos seguros de que se cumplen siempre estas condiciones? ¿Cuáles son los límites de validez de la ley de Darcy?

Se ha supuesto que el movimiento del agua a través de los huecos del suelo es un flujo laminar, es decir, un movimiento ordenado, estratificado o suave. En estas condiciones, el fluido se mueve en láminas paralelas que no se entremezclan y cada partícula de fluido sigue una trayectoria suave, denominada línea de corriente. Esto es así al cumplirse las condiciones de pequeño diámetro de los huecos de la red intersticial y la pequeña velocidad del flujo, que conducen a un número de Reynolds notablemente inferior al crítico. Este número es adimensional, siendo pequeño para flujos laminares y alto para flujos turbulentos. Así, para gradientes hidráulicos elevados, la ley de Darcy no es aplicable, pues la pérdida de carga hidráulica aumenta más rápido que el caudal debido a que el flujo en los huecos pasa de laminar a turbulento.

A partir de numerosos ensayos y por analogía con la hidráulica (Iglesias, 1997), aquí podemos definir el número de Reynolds, R, de la siguiente forma:

donde v es la velocidad del flujo, d es el diámetro medio de los granos, η es el coeficiente de viscosidad del agua y ρ es la densidad del agua.

La linealidad de la ley de Darcy se cumple para R<10. No obstante, la validez de la ley de Darcy es muy habitual en los casos reales, salvo en suelos muy permeables y en las proximidades de algunas captaciones bombeando caudales elevados. Un ejemplo donde no se sigue la ley de Darcy son en las formaciones kársticas. No obstante, con velocidad de flujo muy pequeña, existe un efecto de inercia que limita el flujo laminar que modifican los resultados obtenidos por la ley de Darcy. Sería el caso de la absorción de moléculas de agua que no pueden ser arrastradas por la pequeña velocidad del flujo. Este efecto es más acusado en suelos cohesivos, debido a la presencia de la doble capa alrededor de las partículas del suelo.

Referencias:

IGLESIAS, C. (1997). Mecánica del suelo. Editorial Síntesis, Madrid, 590 pp.

YEPES, V. (2020). Procedimientos de construcción de cimentaciones y estructuras de contención. Colección Manual de Referencia, 2ª edición. Editorial Universitat Politècnica de València, 480 pp. Ref. 328. ISBN: 978-84-9048-903-1.

Licencia de Creative Commons
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

El aprendizaje profundo (deep learning) en la optimización de estructuras

Figura 1. Relación de pertenencia entre la inteligencia artificial, el aprendizaje automático y el aprendizaje profundo

En este artículo vamos a esbozar las posibilidades de la inteligencia artificial en la optimización de estructuras, en particular, el uso del aprendizaje profundo. El aprendizaje profundo (deep learning, DL) constituye un subconjunto del aprendizaje automático (machine learning, ML), que a su vez lo es de la inteligencia artificial (ver Figura 1). Si la inteligencia artificial empezó sobre los años 50, el aprendizaje automático surgió sobre los 80, mientras que el aprendizaje profundo nació en este siglo XXI, a partir del 2010, con la aparición de grandes superordenadores y por el aumento de los datos accesibles. Como curiosidad, uno de los grandes hitos del DL se produjo en 2012, cuando Google fue capaz de reconocer un gato entre los más de 10 millones de vídeos de Youtube, utilizando para ello 16000 ordenadores. Ahora serían necesarios muchos menos medios.

En cualquiera de estos tres casos, estamos hablando de sistemas informáticos capaces de analizar grandes cantidades de datos (big data), identificar patrones y tendencias y, por tanto, predecir de forma automática, rápida y precisa. De la inteligencia artificial y su aplicabilidad a la ingeniería civil ya hablamos en un artículo anterior.

Figura 2. Cronología en la aparición de los distintos tipos de algoritmos de inteligencia artificial. https://www.privatewallmag.com/inteligencia-artificial-machine-deep-learning/

Si pensamos en el cálculo estructural, utilizamos modelos, más o menos sofistificados, que permiten, si se conocen con suficiente precisión las acciones, averiguar los esfuerzos a los que se encuentran sometidos cada uno de los elementos en los que hemos dividido una estructura. Con dichos esfuerzos se identifican una serie de estados límite, que son un conjunto de situaciones potencialmente peligrosas para la estructura y comparar si la capacidad estructural del elemento analizado, dependiente de las propiedades geométricas y de sus materiales constituyentes, supera el valor último de la solicitación a la que, bajo cierta probabilidad, puede llegar a alcanzar el elemento estructural analizado.

Estos métodos tradicionales emplean desde hipótesis de elasticidad y comportamiento lineal, a otros modelos con comportamiento plástico o no lineales más complejos. Suele utilizarse, con mayor o menos sofisticación, el método de los elementos finitos (MEF) y el método matricial de la rigidez. En definitiva, en determinados casos, suelen emplearse los ordenadores para resolver de forma aproximada, ecuaciones diferenciales parciales muy complejas, habituales en la ingeniería estructural, pero también en otros campos de la ingeniería y la física. Para que estos sistemas de cálculo resulten precisos, es necesario alimentar los modelos con datos sobre materiales, condiciones de contorno, acciones, etc., lo más reales posibles. Para eso se comprueban y calibran estos modelos en ensayos reales de laboratorio (Friswell y Mottershead, 1995). De alguna forma, estamos retroalimentando de información al modelo, y por tanto “aprende”.

Figura 2. Malla 2D de elementos finitos, más densa alrededor de la zona de mayor interés. Wikipedia.

Si analizamos bien lo que hacemos, estamos utilizando un modelo, más o menos complicado, para predecir cómo se va a comportar la estructura. Pues bien, si tuviésemos una cantidad suficiente de datos procedentes de laboratorio y de casos reales, un sistema inteligente extraería información y sería capaz de predecir el resultado final. Mientras que la inteligencia artificial debería alimentarse de una ingente cantidad de datos (big data), el método de los elementos finitos precisa menor cantidad de información bruta (smart data), pues ha habido una labor previa muy concienzuda y rigurosa, para intentar comprender el fenómeno subyacente y modelizarlo adecuadamente. Pero, en definitiva, son dos procedimientos diferentes que nos llevan a un mismo objetivo: diseñar estructuras seguras. Otro tema será si éstas estructuras son óptimas desde algún punto de vista (economía, sostenibilidad, etc.).

La optimización de las estructuras constituye un campo científico donde se ha trabajado intensamente en las últimas décadas. Debido a que los problemas reales requieren un número elevado de variables, la resolución exacta del problema de optimización asociado es inabordable. Se trata de problemas NP-hard, de elevada complejidad computacional, que requiere de metaheurísticas para llegar a soluciones satisfactorias en tiempos de cálculo razonables.

Una de las características de la optimización mediante metaheurísticas es el elevado número de iteraciones en el espacio de soluciones, lo cual permite generar una inmensa cantidad de datos para el conjunto de estructuras visitadas. Es el campo ideal para la inteligencia artificial, pues permite extraer información para acelerar y afinar la búsqueda de la solución óptima. Un ejemplo de este tipo es nuestro trabajo (García-Segura et al., 2017) de optimización multiobjetivo de puentes cajón, donde una red neuronal aprendía de los datos intermedios de la búsqueda y luego predecía con una extraordinaria exactitud el cálculo del puente, sin necesidad de calcularlo. Ello permitía reducir considerablemente el tiempo final de computación.

Sin embargo, este tipo de aplicación es muy sencilla, pues solo ha reducido el tiempo de cálculo (cada comprobación completa de un puente por el método de los elementos finitos es mucho más lenta que una predicción con una red neuronal). Se trata ahora de dar un paso más allá. Se trata de que la metaheurística sea capaz de aprender de los datos recogidos utilizando la inteligencia artificial para ser mucho más efectiva, y no solo más rápida.

Tanto la inteligencia artificial como el aprendizaje automático no son una ciencia nueva. El problema es que sus aplicaciones eran limitadas por la falta de datos y de tecnologías para procesarlas de forma rápida y eficiente. Hoy en día se ha dado un salto cualitativo y se puede utilizar el DL, que como ya hemos dicho es una parte del ML, pero que utiliza algoritmos más sofisticados, construidos a partir del principio de las redes neuronales. Digamos que el DL (redes neuronales) utiliza algoritmos distintos al ML (algoritmos de regresión, árboles de decisión, entre otros). En ambos casos, los algoritmos pueden aprender de forma supervisada o no supervisada. En las no supervisadas se facilitan los datos de entrada, no los de salida. La razón por la que se llama aprendizaje profundo hace referencia a las redes neuronales profundas, que utilizan un número elevado de capas en la red, digamos, por ejemplo, 1000 capas. De hecho, el DL también se le conoce a menudo como “redes neuronales profundas”. Esta técnica de redes artificiales de neuronas es una de las técnicas más comunes del DL.

Figura. Esquema explicativo de diferencia entre ML y DL. https://www.privatewallmag.com/inteligencia-artificial-machine-deep-learning/

Una de las redes neuronales utilizadas en DL son las redes neuronales convolucionales, que es una variación del perceptrón multicapa, pero donde su aplicación se realiza en matrices bidimensionales, y por tanto, son muy efectivas en las tareas de visión artificial, como en la clasificación y segmentación de imágenes. En ingeniería, por ejemplo, se puede utilizar para la monitorización de la condición estructural, por ejemplo, para el análisis del deterioro. Habría que imaginar hasta dónde se podría llegar grabando en imágenes digitales la rotura en laboratorio de estructuras de hormigón y ver la capacidad predictiva de este tipo de herramientas si contaran con suficiente cantidad de datos. Todo se andará. Aquí os dejo una aplicación tradicional típica (Antoni Cladera, de la Universitat de les Illes Balears), donde se explica el modelo de rotura de una viga a flexión en la pizarra y luego se rompe la viga en el laboratorio. ¡Cuántos datos estamos perdiendo en la grabación! Un ejemplo muy reciente del uso del DL y Digital Image Correlation (DIC) aplicado a roturas de probetas en laboratorio es el trabajo de Gulgec et al. (2020).

Sin embargo, aquí nos interesa detenernos en la exploración de la integración específica del DL en las metaheurísticas con el objeto de mejorar la calidad de las soluciones o los tiempos de convergencia cuando se trata de optimizar estructuras. Un ejemplo de este camino novedoso en la investigación es la aplicabilidad de algoritmos que hibriden DL y metaheurísticas. Ya hemos publicado algunos artículos en este sentido aplicados a la optimización de muros de contrafuertes (Yepes et al., 2020; García et al., 2020a, 2020b). Además, hemos propuesto como editor invitado, un número especial en la revista Mathematics (indexada en el primer decil del JCR) denominado “Deep learning and hybrid-metaheuristics: novel engineering applications“.

Dejo a continuación un pequeño vídeo explicativo de las diferencias entre la inteligencia artificial, machine learning y deep learning.

Referencias:

FRISWELL, M.; MOTTERSHEAD, J. E. (1995). Finite element model updating in structural dynamics (Vol. 38). Dordrecht, Netherlands: Springer Science & Business Media.

GARCÍA, J.; MARTÍ, J.V.; YEPES, V. (2020a). The buttressed  walls problem: An application of a hybrid clustering particle swarm optimization algorithm. Mathematics,  8(6):862. https://doi.org/10.3390/math8060862

GARCÍA, J.; YEPES, V.; MARTÍ, J.V. (2020b). A hybrid k-means cuckoo search algorithm applied to the counterfort retaining walls problem. Mathematics,  8(4), 555. DOI:10.3390/math8040555

GARCÍA-SEGURA, T.; YEPES, V.; FRANGOPOL, D.M. (2017). Multi-Objective Design of Post-Tensioned Concrete Road Bridges Using Artificial Neural Networks. Structural and Multidisciplinary Optimization, 56(1):139-150. DOI:1007/s00158-017-1653-0

GULGEC, N.S.; TAKAC, M., PAKZAD S.N. (2020). Uncertainty quantification in digital image correlation for experimental evaluation of deep learning based damage diagnostic. Structure and Infrastructure Engineering, https://doi.org/10.1080/15732479.2020.1815224

YEPES, V.; MARTÍ, J.V.; GARCÍA, J. (2020). Black hole algorithm for sustainable design of counterfort retaining walls. Sustainability, 12(7), 2767. DOI:10.3390/su12072767

Licencia de Creative Commons
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

El misterio de los muros serpenteantes “crinkle crankle walls”

Figura 1. “Crinkle crankle wall” localizado en Bramfield, Suffolk. Wikipedia

A veces una imagen es muy eficaz para explicar un concepto aparentemente sencillo como la influencia del momento de inercia en la resistencia de una sección estructural. Para eso utilicé los llamados “muros serpenteantes“, también llamados “crinkle crankle walls“, muros que se popularizaron en el Reino Unido en el siglo XVIII. Lo digo porque el otro día puse en Twitter una pregunta aparentemente sencilla como la siguiente: “¿Por qué creéis que en Inglaterra a veces nos encontramos con este tipo de muros ondulados? ¿Se trata de algo decorativo? Tiene una explicación mucho más profunda“. Es una pregunta típica que suelo hacer a mis estudiantes para que incentivarles al pensamiento crítico y para que puedan enlazar conceptos que aprendieron en otras asignaturas.

La sorpresa ha sido mayúscula. El tuit ha sido retuiteado y comentado muchísimo más de lo que esperaba. Muchas contestaciones han sido correctas. Otras, incluso siendo correctas, son muy creativas.

La verdad es que la forma ondulada permite un aumento considerable del momento de inercia de la sección, lo cual permite reducir las tensiones provocadas por el momento flector en la base. Esto permite reducir la cantidad de ladrillos necesarios en el caso de ser un muro recto: se tendría que realizar un muro doble y, probablemente, reforzar con algún pilar intermedio o contrafuerte, dependiendo de la altura del muro y de las acciones previstas, especialmente el viento. La solución, como veis, es bastante sencilla, con unos conocimientos muy básicos de resistencia de materiales y cálculo estructural. Lo que es evidente, es que esta geometría precisa de cierta destreza por parte de los oficiales que ejecutan el muro, y algo más de tiempo.

Sin embargo, las respuestas recibidas van más allá de esta consideración. Os voy a comentar algunas de ellas para que veáis que la inteligencia colectiva, a veces, ofrece soluciones de lo más creativas.

Por ejemplo, Amaia López nos ilustra un ejemplo de muro serpenteante que se encuentra en nuestro país, en concreto, en Caldes de Montbui (Barcelona).

Figura 2. Muro serpenteante en Caldes de Montbui (Barcelona). Fuente: Amaia López

Otros son más creativos, como Rafael Naranjo, que nos dice que podría ser la forma para defender ciertas posiciones en la batalla, aunque creo que en Inglaterra estos muros no tienen mucho que ver con este tipo de estrategias bélicas. También muchas respuestas han comentado el aumento de la estabilidad del muro, aunque para eso tenemos el cimiento, que debería ser quien asegurara este estado límite. Alguno se inclina por hablar de las ondas sísmicas y su afección al muro. Por cierto, alguien ha querido traducir “crinkle crankle” como “cigüeña arrugada”, aunque yo me quedo mejor con el nombre de “muro serpenteante”.

Metidos en Carretera (@MetEnCarretera) nos ofrece una explicación con el símil de algunas soluciones prefabricadas, para ganar canto sin incrementar el espesor del muro. Este es un buen ejemplo.

Figura 3. Ejemplo de muro prefabricado. Fuente: @MetEnCarretera

Otras explicaciones apuntan al efecto arco que presenta el muro, haciendo que los efectos de flexión se transformen en compresión. Eso me recuerda a la solución genial de Eduardo Torroja para la cubierta del hipódromo de la Zarzuela, aunque la diferencia es que el muro serpenteante tiene una sola curvatura, y la cubierta citada tiene doble curvatura. Una idea sería usar esta forma para muros de contención prefabricados. Ahí lo dejo.

Figura 4. Hipódromo de la Zarzuela. Wikipedia

Interesante la puntualización de Luis Bañón (@luisbanon) respecto al problema que pueden presentar estos muros delgados si choca frontalmente un vehículo debido al punzonamiento. Santiago Calvo nos da un motivo agrícola, como es la ampliación de la superficie de cultivo de fruta aprovechando las zonas de sombra que proporciona esta geometría, y también un motivo estético, como es su uso en la Universidad de Virginia. Quisco Mena, incluso, argumenta que, además de la inercia, esta forma permite eliminar las juntas de dilatación.

Como resumen, no dejo de sorprenderme cada día en las redes sociales. A veces hay mucha tontería, pero otras veces se aprende. Este es un ejemplo de interactuar con mis estudiantes y abrir un debate interesante en redes.

Os dejo algunos vídeos de esta tipología de muro. También podéis ver muchas fotografías de esta tipología aquí: https://www.boredpanda.es/muros-ondulados/?utm_source=google&utm_medium=organic&utm_campaign=organic

Licencia de Creative Commons
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

La excavación por bataches

Figura 1. Excavación por bataches (Cano et al., 2020). Aunque es posible hacerlo en módulo de dos, es preferible hacerlos en módulo de tres, según Figura 4.

Cuando se está realizando una excavación para el vaciado, por ejemplo, de unos sótanos de un edificio, lo primero que se plantea es si es necesario algún sistema de contención provisional (muros pantalla, muro berlinés, tablestacas, suelo armado o apuntalamiento provisional) hasta que se permita construir unos muros o estructuras de contención definitiva de las tierras. Sin embargo, a veces no se precisa de una estructura de contención provisional, pues se puede ejecutar, bajo determinadas condiciones, el vaciado mediante una excavación vertical o en talud, mediante bermas o bien mediante bataches. Este artículo explica la excavación por bataches.

La primera consideración a tener en cuenta es que solo se podrán acometer excavaciones sin una contención provisional en el caso de que no se vea perjudicada por las aguas subterráneas o cuando no exista afección sobre estructuras vecinas o servicios públicos. Por tanto, la excavación por bataches solo será aplicable en el caso de que el vaciado se encuentre por encima del nivel freático, no existan cimentaciones próximas y se puedan mantener los taludes estables o se puedan apuntalar. En este caso, la excavación por bataches permite el vaciado mediante etapas. El sistema se basa en la excavación alterna de tramos del frente de una berma perimetral previamente ejecutada. En el caso de edificaciones, la excavación por bataches es habitual para un solo sótano, aunque se podrían excavar dos o tres sótanos con un sistema más complejo basado en la creación de anillos descendentes, normalmente anclados.

Tal y como se muestra en la Figura 2, el batache es la excavación que queda vertical entre dos espaldones, que actúan a modo de contrafuerte de terreno. Según la norma NTE-ADZ, el ancho E del batache no podrá superar los 2 m, ni tampoco podrá superar la altura vertical del espaldón HE, los 3 m (caso de realizar la excavación con maquinaria). En caso de que alguno de estos dos parámetros se incumpla, deberá procederse al entibado.

Con todo, hay que tener presente que en España las antiguas Normas Tecnológicas de la Edificación, NTE, del Ministerio de la Vivienda, se encuentran en desuso, haciendo referencia de forma genérica al ancho de excavación, sin tener en cuenta los parámetros geotécnicos del terreno. Por tanto, estas dimensiones límite de las NTE deben ser indicativas, pues se debería efectuar un estudio en mayor profundidad con datos reales para ajustar los límites en casos complejos. Por ejemplo, los anchos de los bataches podrían llegar incluso a 3-5 m en algunos casos concretos que requerirían un estudio en detalle, incluso la entibación.

Además, la norma NTE-CCT impone otra serie de restricciones a la hora de ejecutar un batache. Así, la berma superior del espaldón B deberá ser mayor a la mitad de la anchura E del batache; la distancia de la parte inferior del espaldón al paramento vertical A deberá ser mayor que su altura HE; además, la anchura del espaldón NE, deberá ser mayor a A.

Figura 2. Esquema de batache, con las condiciones impuestas por NTE-CCT

Un aspecto de obra de gran interés es hacer coincidir el ancho E del batache con las dimensiones de las placas de encofrado. Sin embargo, la excavación deberá ser algo superior a la dimensión del elemento hormigonado, pues se debe permitir la presencia de las esperas de las armaduras horizontales. El exceso puede estimarse en unos 60 cm en cada lado, con un mínimo de 20-30 cm si se opta por doblar las armaduras. Por tanto, un batache de 2 m puede irse a unos 3 m, lo cual puede poner en riesgo la estabilidad de un terreno de baja cohesión durante la construcción (Cano et al., 2020).

El aspecto más importante de la excavación por bataches es el orden de ejecución, puesto que la excavación se realiza por tramos alternados para que el sostenimiento sea viable, buscando el efecto arco del terreno entre los espaldones para evitar el derrumbe. Hay que tener en cuenta que, una vez descubiertos los bataches, deben cubrirse por los muros lo más rápidamente posible, como mucho al día siguiente del descubrimiento del batache. Un posible orden de ejecución de los tramos podría ser el descrito en las Figuras 3 y 4. En primer lugar, se excavaría el batache A, ejecutándose dicho tramo de muro. A continuación se procede de la misma forma con el tramo B, y por último, con el C. Hay que tener en cuenta que la excavación mediante bataches normalmente se encofra a una sola cara el muro, dejando la otra sobre el terreno.

Figura 3. El proceso de ejecución de los muros que sostienen un vaciado empieza con el replanteo de los bataches A, B y C.

 

Figura 4. Posteriormente, empieza la excavación con los bataches A, debiéndose terminar completamente el muro de dicho tramo. Luego siguen los bataches B y C.

En la Figura 5 se observa el encofrado a una cara del muro de sótano y el ferrallado de un batache. Corresponde a la ejecución de un aparcamiento subterráneo.

Figura 5. Ferrallado de un batache en aparcamiento. http://www.parkingvejer.com/index.php?page=hitos.php&lang=#prettyPhoto/62/

Os dejo un vídeo que explica el procedimiento constructivo de muros mediante excavación por bataches. Espero que os sea útil.

En este otro vídeo, de Marcelo Pardo, también se explica el procedimiento constructivo de un muro de contención por la técnica de bataches.

A continuación os dejo las normas NTE-ADZ y NTE-CCT para su consulta.

Descargar (PDF, 1.14MB)

Descargar (PDF, 199KB)

Comparto este interesante trabajo de la universidad de Alicante en el que se estima la longitud máxima de los bataches para construir un muro de contención:

Descargar (PDF, 2.92MB)

Referencias:

CANO, M.; PASTOR, J.L.; MIRANDA, T.; TOMÁS, R. (2020). Procedimiento constructivo de muros de sótano mediante bataches con juntas de conexión. Estudio del ancho óptimo de excavación en suelos mixtos. Informes de la Construcción, 72:558. http://informesdelaconstruccion.revistas.csic.es/index.php/informesdelaconstruccion/article/view/6008/7299

YEPES, V. (2020). Procedimientos de construcción de cimentaciones y estructuras de contención. Colección Manual de Referencia, 2ª edición. Editorial Universitat Politècnica de València, 480 pp. Ref. 328. ISBN: 978-84-9048-903-1.

 

Licencia de Creative Commons
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.