nomograma – El blog de Víctor Yepes

Cálculo de la producción de un compactador

Figura 1. Compactador monocilíndrico vibratorio autopropulsado Cat CS10 GC. https://www.interempresas.net/ObrasPublicas/Articulos/346172-Caterpillar-presenta-sus-nuevos-compactadores-vibratorios-de-suelos-de-un-solo-tambor.html

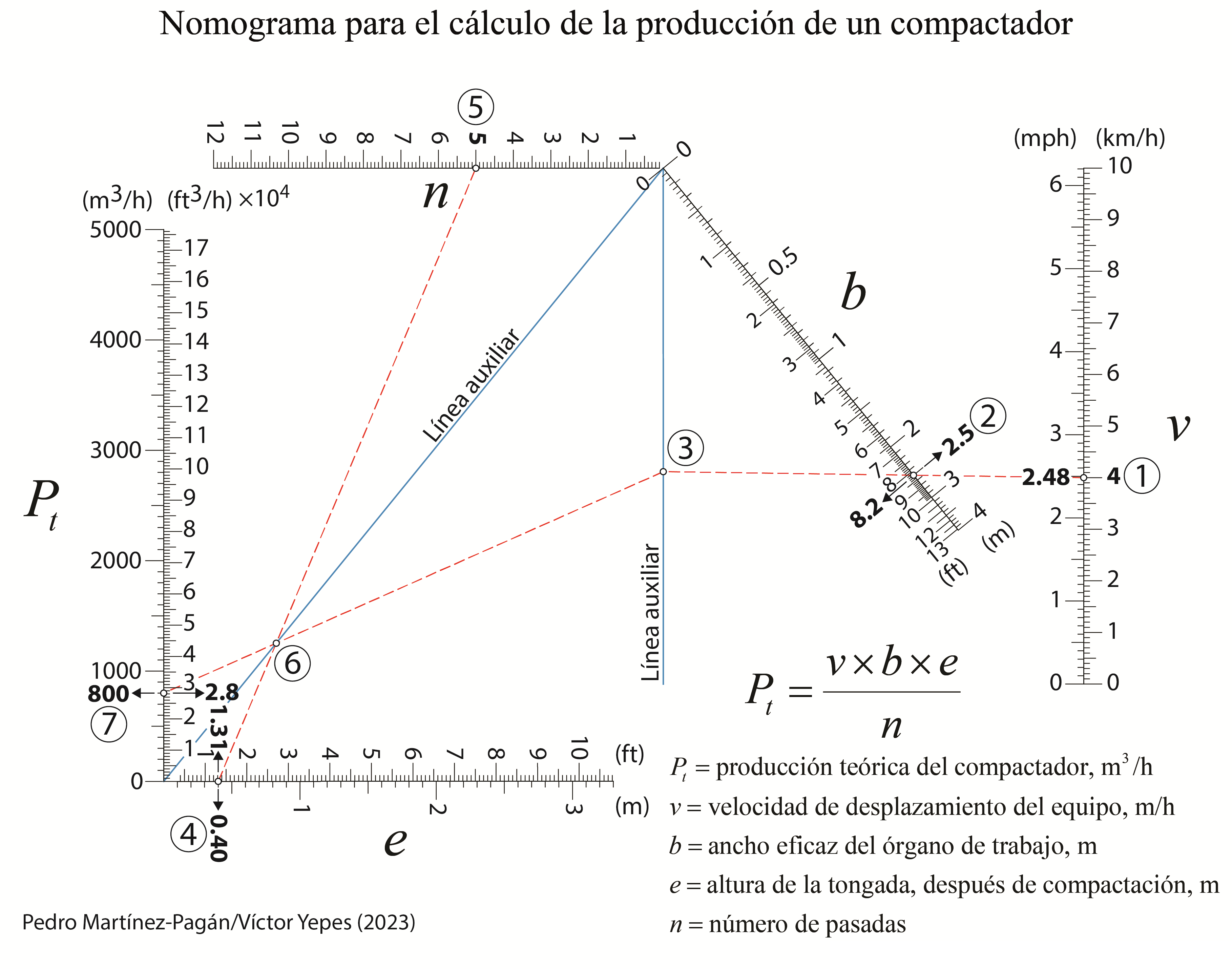
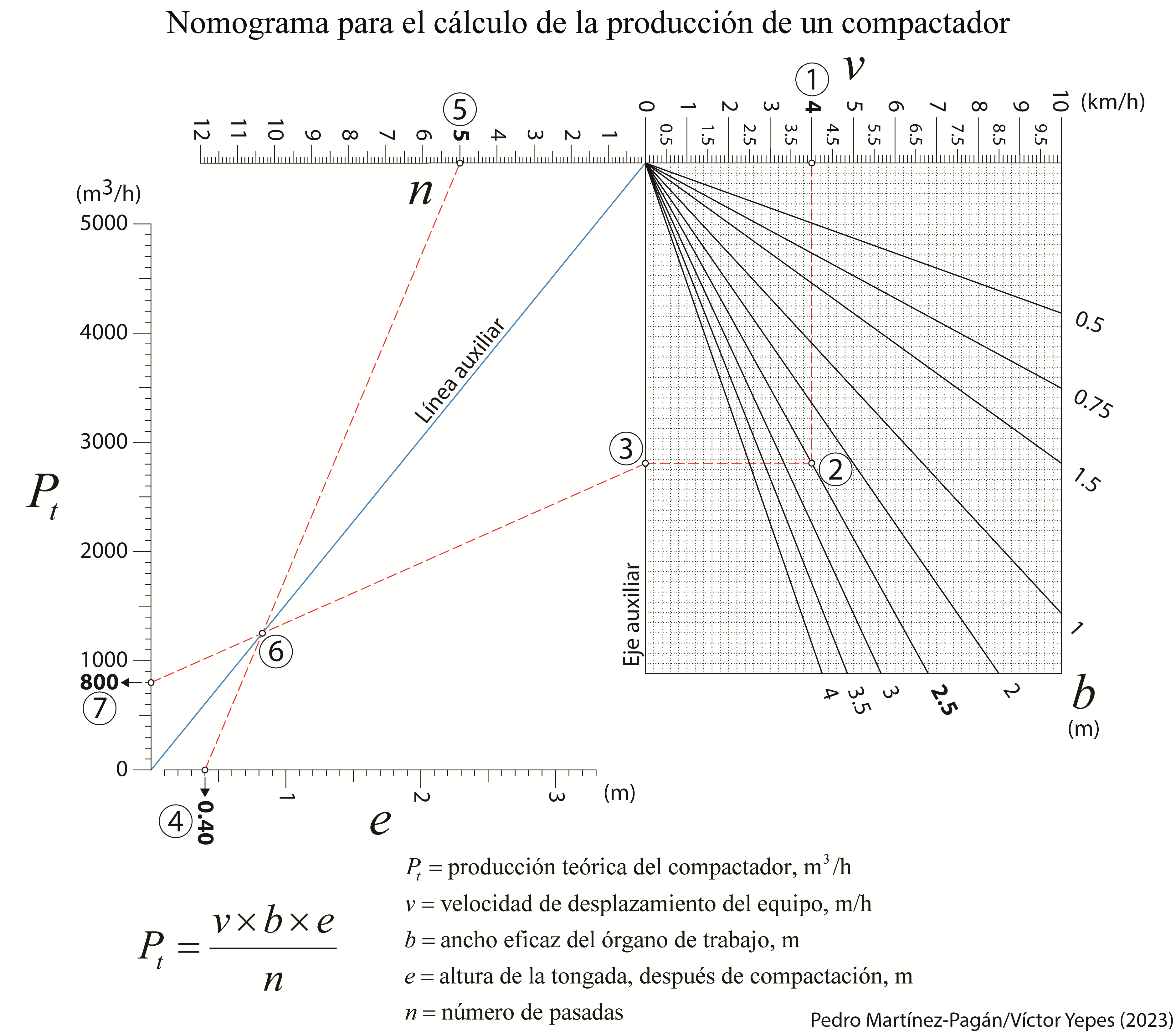
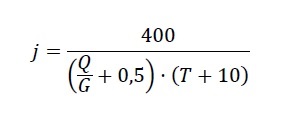La producción de un compactador es directamente proporcional a su velocidad de trabajo, al ancho eficaz del compactador y al espesor de la tongada una vez compactada, e inversamente proporcional al número de pasadas necesarias. El ancho eficaz sería la diferencia entre la anchura del órgano de trabajo del compactador y el solape necesario para garantizar la compactación entre los distintos carriles.

Debido a la multitud de factores que influyen en la compactación, para grandes volúmenes de obra, se aconseja la realización de tramos de prueba, donde se pueden establecer los criterios que, bajo la perspectiva económica, sean óptimos para llegar a la compactación especificada. Los tramos de prueba no suelen estar justificados en el caso de que los materiales sean suficientemente homogéneos y siempre resulta interesante cuando nos encontramos ante yacimientos importantes. En otro caso, no resulta económica su ejecución. Estos tramos de prueba están formados por una cuña, cuyo espesor llega hasta el máximo que se considere para el equipo empleado.

Este tipo de cuestiones se tratan ampliamente en el curso sobre “Compactación superficial y profunda de suelos en obras de ingeniería civil y edificación”. Toda la información la puedes encontrar en esta página: https://ingeoexpert.com/cursos/curso-de-compactacion-superficial-y-profunda-de-suelos-en-obras-de-ingenieria-civil-y-edificacion/. Además, este os recomiendo también el curso sobre “Gestión de costes y producción de la maquinaria empleada en la construcción”, cuya información podéis ver aquí: https://ingeoexpert.com/cursos/curso-de-gestion-de-costes-y-produccion-de-la-maquinaria-empleada-en-la-construccion/

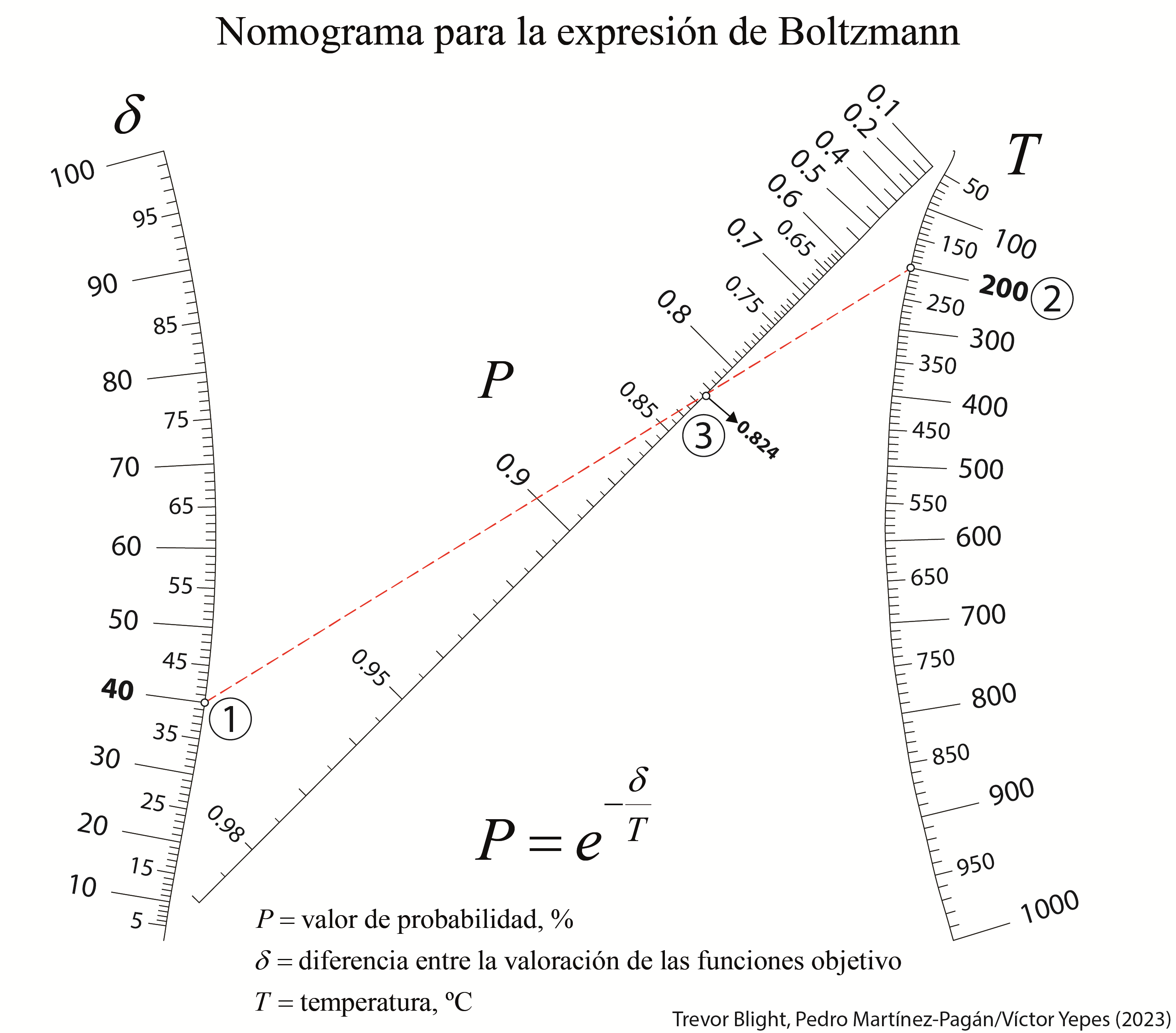
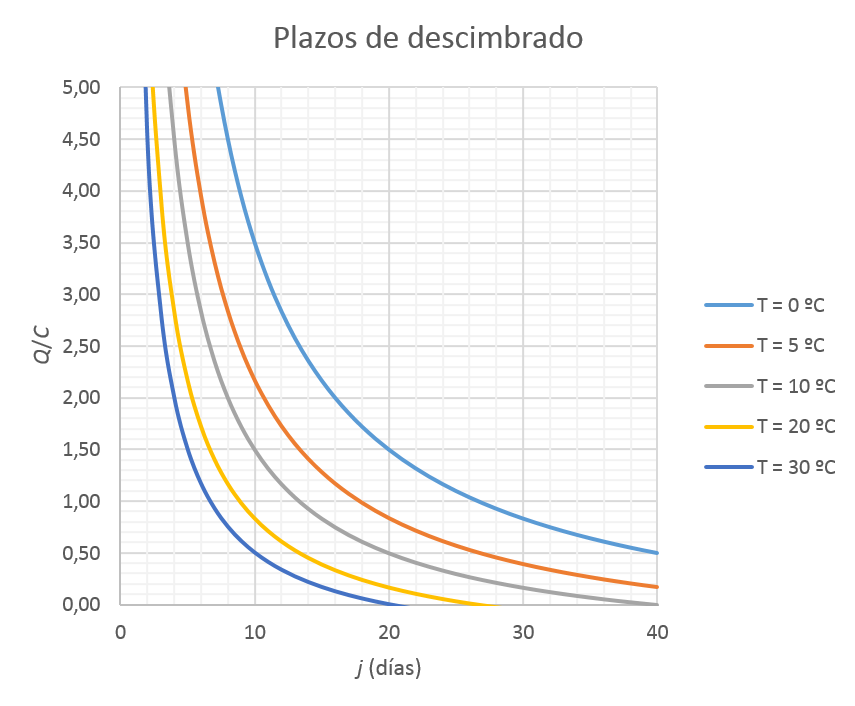
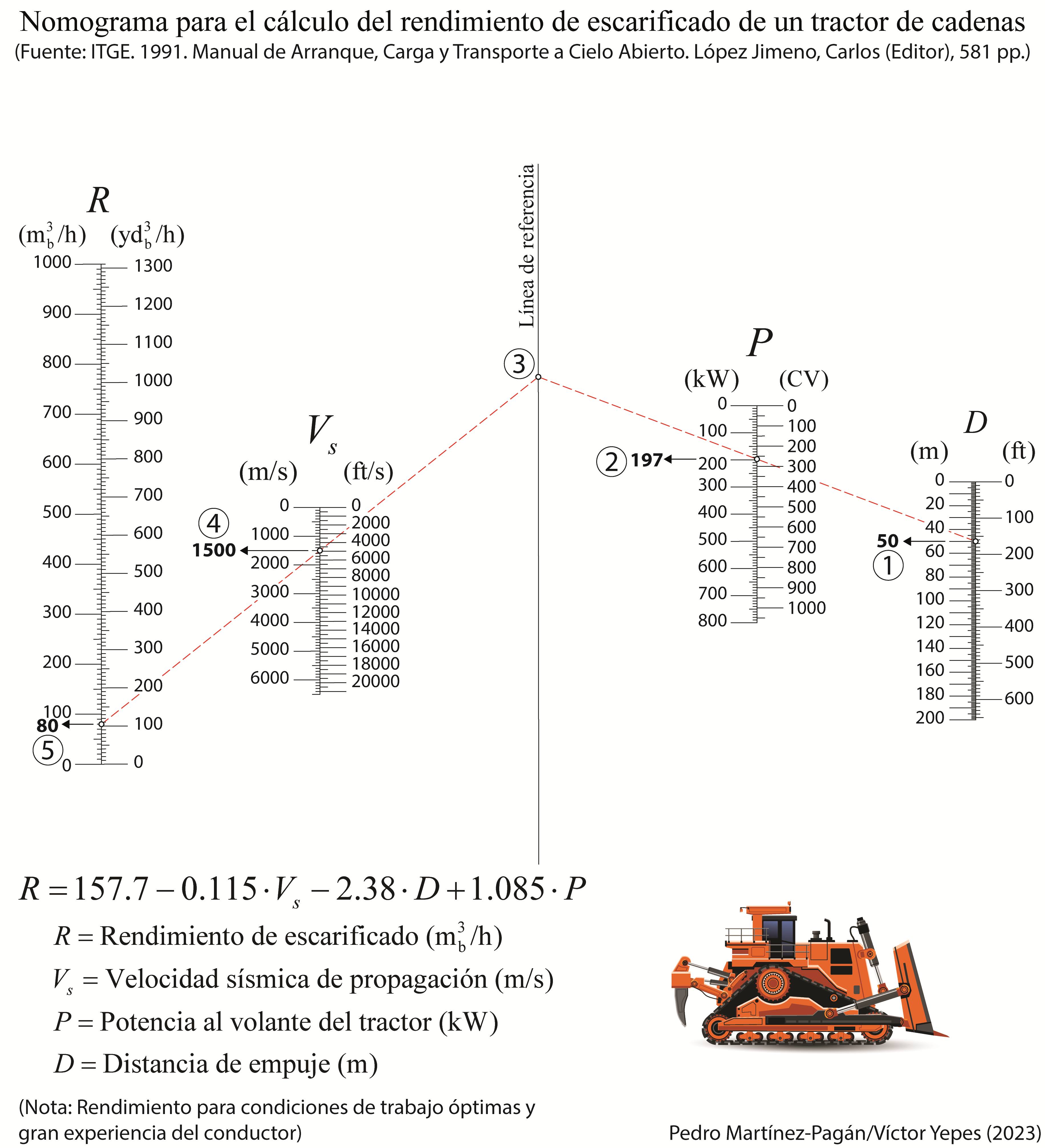
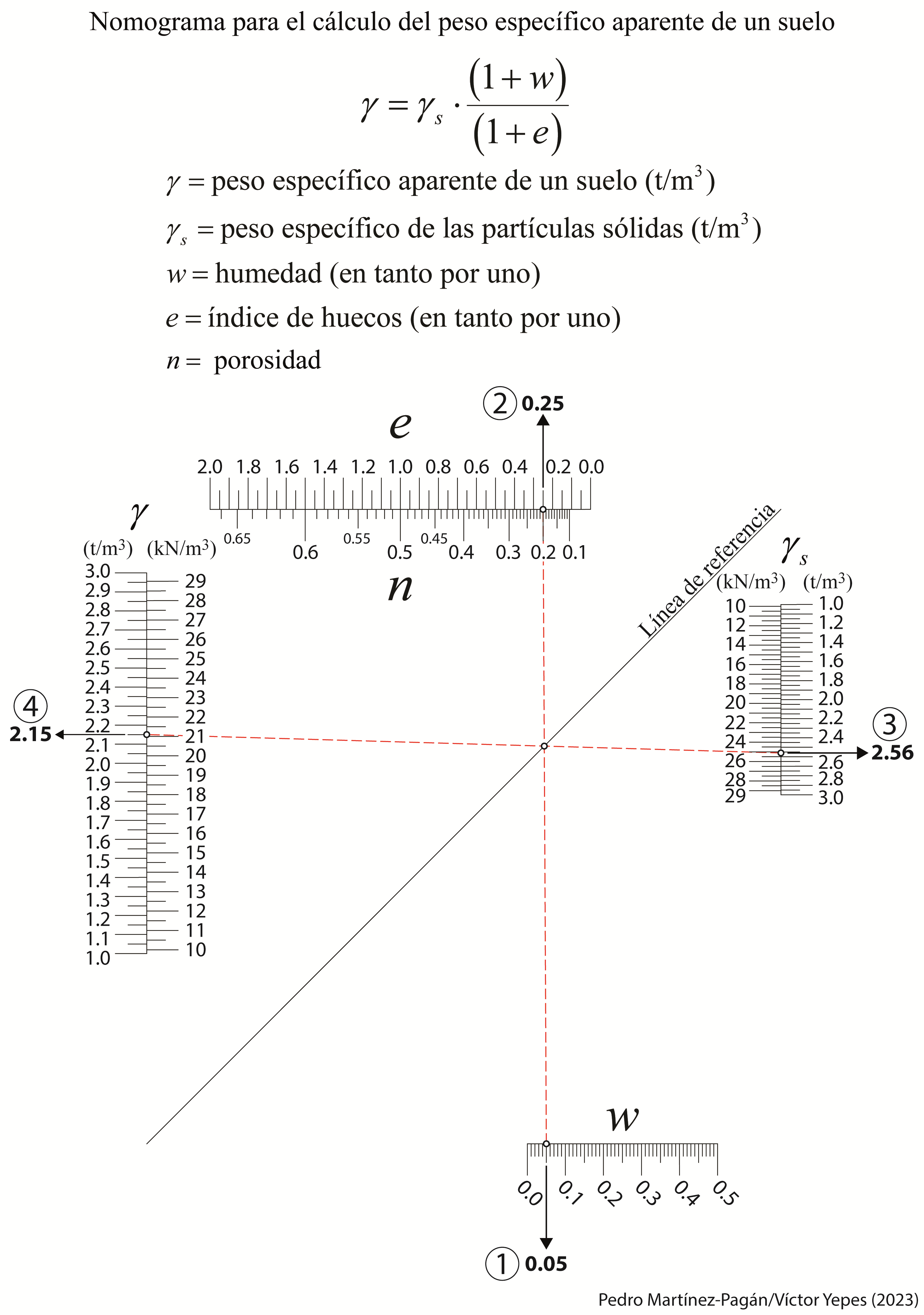
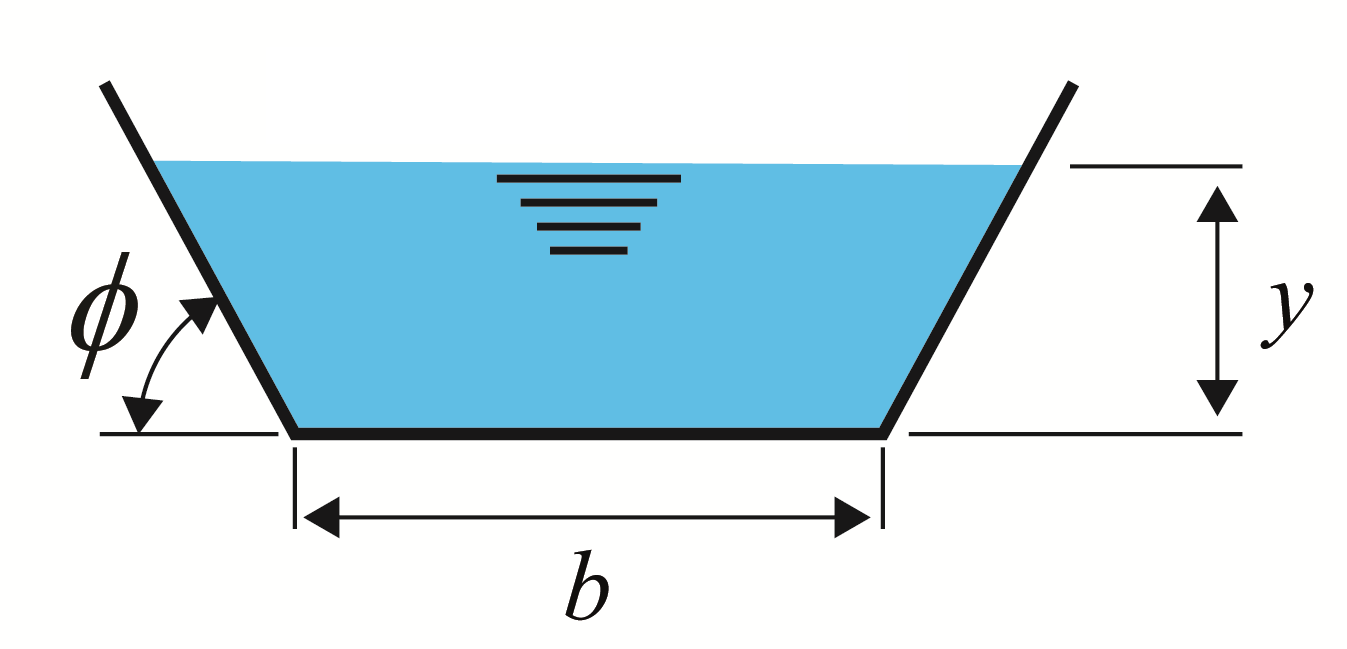
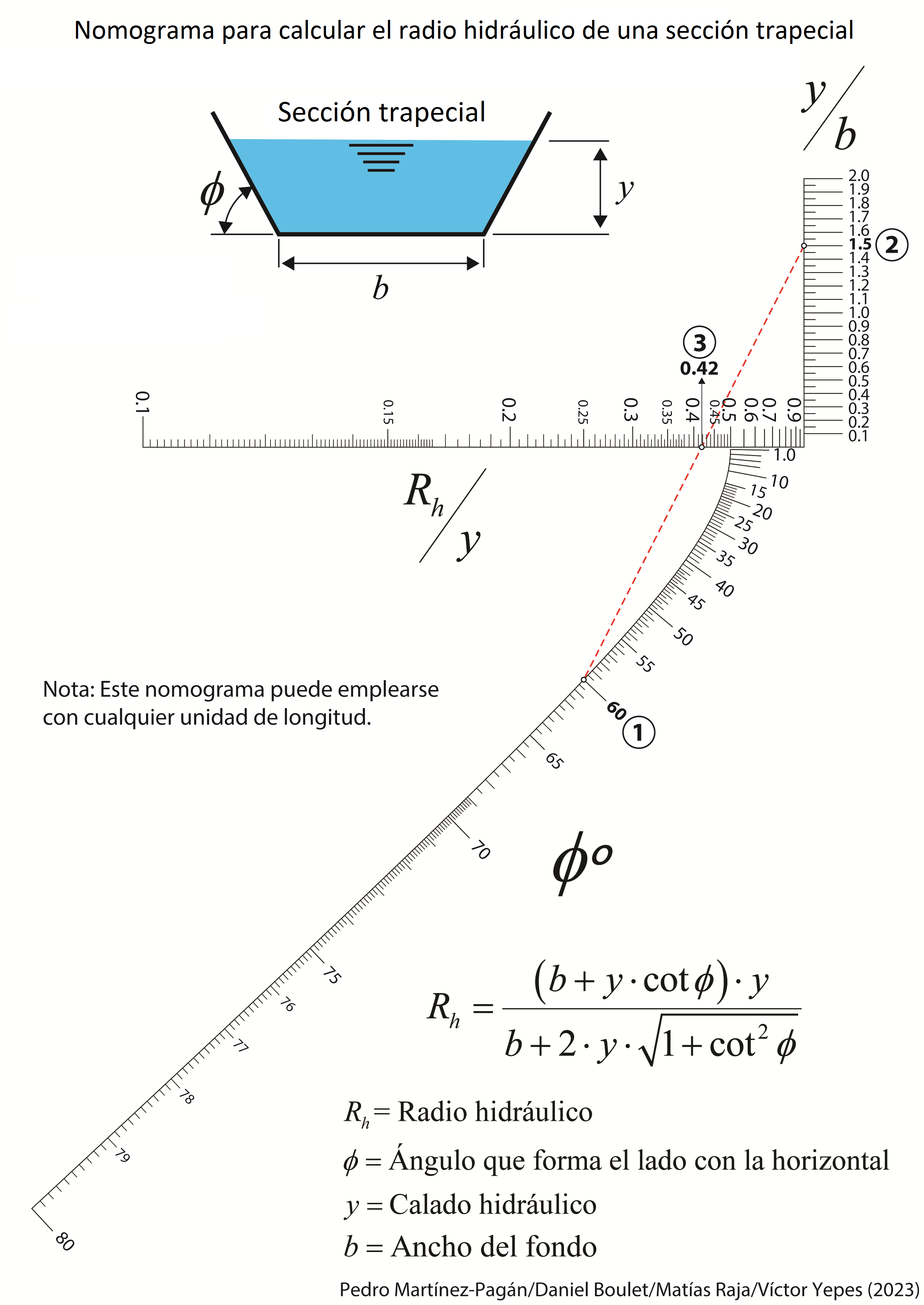
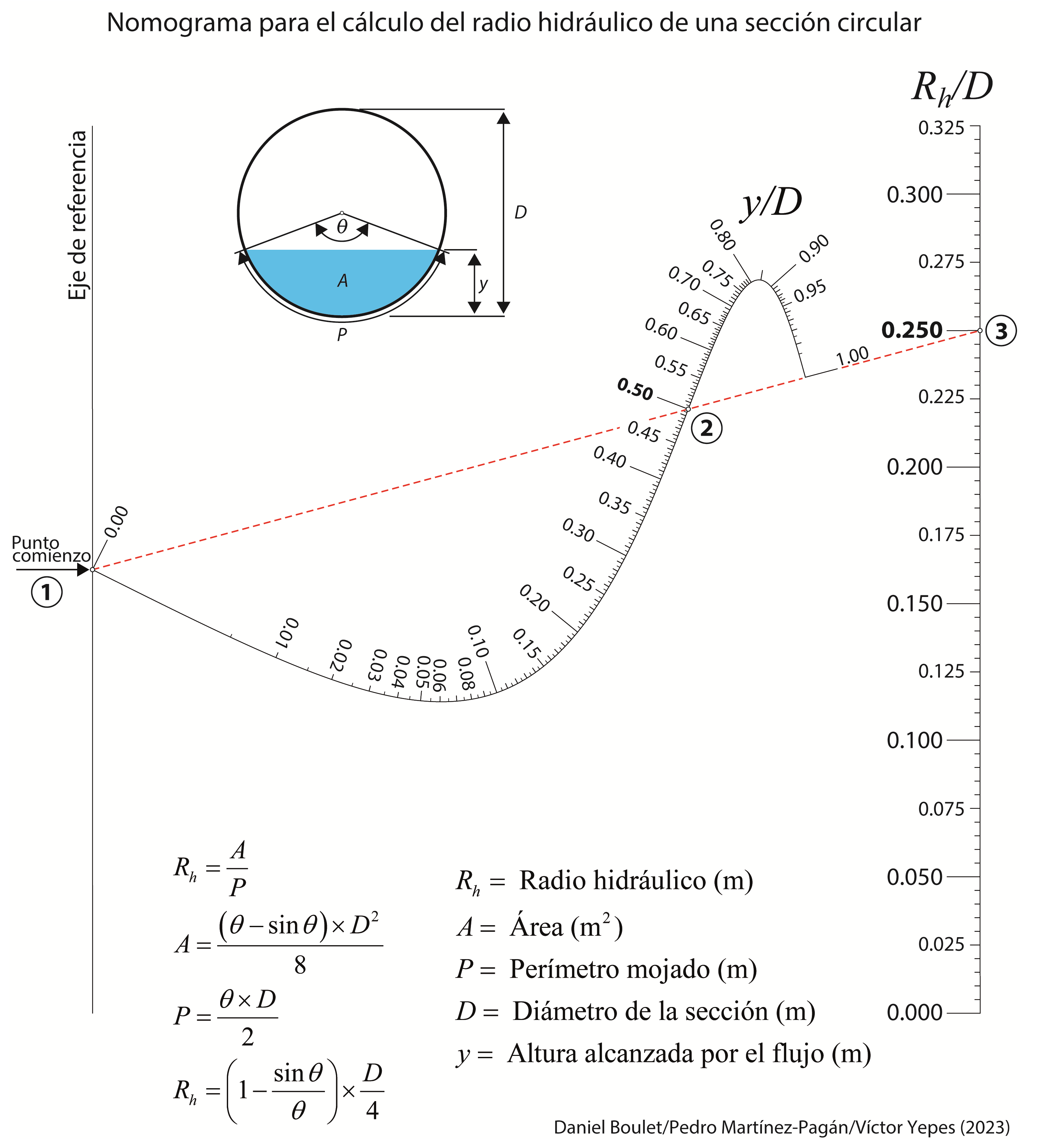
A continuación os dejo un par de nomogramas que permiten el cálculo directo de esta producción. En uno de ellos se han utilizado tanto las unidades del sistema internacional como las anglosajonas. Estos nomogramas se han elaborado en colaboración con el profesor Pedro Martínez Pagán, de la Universidad Politécnica de Cartagena.

Referencias:

MORILLA, I. (2012). Interpretación de los ensayos geotécnicos en suelos. 627 pp., Madrid.

YEPES, V. (1997). Equipos de movimiento de tierras y compactación. Problemas resueltos. Colección Libro Docente n.º 97.439. Ed. Universitat Politècnica de València. 253 pág. ISBN: 84-7721-551-0.

YEPES, V. (2021). Procedimientos de construcción para la compactación y mejora del terreno. Colección Manual de Referencia, 1ª edición. Editorial Universitat Politècnica de València, 426 pp. Ref. 428. ISBN: 978-84-9048-603-0.

YEPES, V. (2022). Gestión de costes y producción de maquinaria de construcción. Colección Manual de Referencia, serie Ingeniería Civil. Editorial Universitat Politècnica de València, 243 pp. Ref. 442. ISBN: 978-84-1396-046-3

YEPES, V. (2023). Maquinaria y procedimientos de construcción. Problemas resueltos. Colección Académica. Editorial Universitat Politècnica de València, 562 pp. Ref. 376. ISBN 978-84-1396-174-3

Cursos:

Curso de compactación superficial y profunda de suelos en obras de ingeniería civil y edificación.

Curso de gestión de costes y producción de la maquinaria empleada en la construcción.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Analogía física y conceptos fundamentales de la metaheurística “Simulated Annealing”

Figura 1. Proceso de recocido del acero. https://www.win-therm.com.my/what-is-annealing-heat-treatment-process-annealing/

En un artículo anterior describimos la metaheurística conocida como “Recocido simulado” o “Cristalización simulada”, que en inglés se conoce como “Simulated Annealing”. Para los que no estéis familiarizados con la optimización, os dejo en este enlace una descripción de lo que son las metaheurísticas.

En la década de 1980, Kirkpatrick et al. (1983), mientras trabajaban en el diseño de circuitos electrónicos, y de manera independiente, Cerny (1985), investigando el problema del TSP (Traveling Salesman Problem), consideraron la aplicación del algoritmo de Metrópolis en algunos de los desafíos de optimización combinatoria que surgen en este tipo de diseño. Para lograrlo, creyeron que era posible establecer una analogía entre los parámetros presentes en la simulación termodinámica y aquellos que se encuentran en los métodos de optimización local. En la Figura 2 se puede ver dicha analogía.

Figura 2. Analogía entre la termodinámica y la optimización (Díaz *et al*., 1996)

Como se puede observar, en el ámbito de la optimización, el concepto físico de temperatura no tiene un significado literal, sino que debe ser considerado como un parámetro, T, que necesita ser ajustado. De esta manera, podemos encontrar similitudes entre los procesos que tienen lugar cuando las moléculas de una sustancia se distribuyen en diferentes niveles energéticos en busca de un equilibrio a una temperatura específica y los procesos de minimización en la optimización local (o, en el caso de maximización, de manera similar).

En el primer caso, con una temperatura fija, la distribución de las partículas sigue la distribución de Boltzmann. Por lo tanto, cuando una molécula se desplaza, su movimiento será aceptado en la simulación si esto resulta en una disminución de la energía, o con una probabilidad proporcional al factor de Boltzmann si no es así. En el contexto de la optimización, al fijar el parámetro T, introducimos una perturbación y aceptamos directamente la nueva solución si su costo disminuye, o bien con una probabilidad proporcional al “factor de Boltzmann” en caso contrario.

La clave del recocido simulado es su estrategia heurística de búsqueda local. La elección del nuevo elemento del entorno, N(s), se hace de manera aleatoria, lo que puede llevar a quedar atrapado en óptimos locales. Para evitar esto, el recocido simulado permite, con una probabilidad decreciente a medida que nos acercamos a la solución óptima, el movimiento hacia soluciones peores. Al analizar el factor de Boltzmann en función de la temperatura, observamos que a medida que esta disminuye, la probabilidad de aceptar una solución peor disminuye rápidamente.

Figura 3. Valor del factor de Boltzmann en función de la temperatura y de δ (Díaz *et al*., 1996)

En consecuencia, la estrategia a seguir en el recocido simulado implica comenzar con una temperatura alta. Esto permite la posibilidad de aceptar soluciones peores en las primeras etapas, cuando estamos a gran distancia del óptimo global. A medida que se avanza hacia el óptimo global, se reducirá gradualmente la temperatura, disminuyendo así la probabilidad de aceptar soluciones peores. El nombre de este algoritmo proviene del proceso metalúrgico de “recocido” utilizado, por ejemplo, para eliminar las tensiones internas en el acero laminado en frío. En este proceso, el material se somete a un calentamiento rápido y luego se enfría de manera lenta y controlada durante horas.

A continuación os dejo un nomograma, elaborado junto con los profesores Trevor Blight y Pedro Martínez Pagán, para calcular la probabilidad en función de la temperatura y de δ. Aquí también resulta sencillo comprobar cómo varía dicha probabilidad en función de los valores anteriores.

Os dejo también un vídeo explicativo:

Referencias

CERNY, V. (1985). Thermodynamical approach to the traveling salesman problem: an efficient simulated algorithm. Journal of Optimization Theory and Applications, 45: 41-51.

DÍAZ, A. et al. (1996). Optimización heurística y redes neuronales en dirección de operaciones e ingeniería. Editorial Paraninfo, Madrid, 235 pp.

KIRKPATRICHK, S.; GELATT, C.D.; VECCHI, M.P. (1983). Optimization by simulated annealing. Science, 220(4598): 671-680.

LUNDY, M.; MEES, A. (1986). Convergence of an Annealing Algorithm. Mathematical programming, 34:111-124.

METROPOLIS, N.; ROSENBLUTH, A.W.; ROSENBLUTH, M.N.; TELLER, A.H.; TELER, E. (1953). Equation of State Calculation by Fast Computing Machines. Journal of Chemical Physics, 21:1087-1092.

GONZÁLEZ-VIDOSA-VIDOSA, F.; YEPES, V.; ALCALÁ, J.; CARRERA, M.; PEREA, C.; PAYÁ-ZAFORTEZA, I. (2008) Optimization of Reinforced Concrete Structures by Simulated Annealing. TAN, C.M. (ed): Simulated Annealing. I-Tech Education and Publishing, Vienna, pp. 307-320. (link)

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Nomograma para la estimación del plazo de descimbrado según el Código Estructural

Figura 1. Desencofrado parcial de un muro de hormigón armado. Imagen: V. Yepes (2023)

En un artículo anterior ya se habló del cimbrado, recimbrado, clareado y descimbrado de plantas consecutivas de un edificio. Allí se recogieron recomendaciones para estimar el plazo de descimbrado de una estructura de hormigón.

El plazo mínimo de descimbrado depende de la evolución de la resistencia, del módulo de deformación, de las condiciones de curado, de las características de la estructura y de la relación entre la carga muerta y la carga actuante en el momento del descimbrado. Esta operación comienza quitando los puntales de las zonas más deformables del forjado (extremo de los voladizos y centros de vano) para continuar hacia los apoyos. Esto se hace para no cargar más de lo previsto y que se deforme el forjado de forma brusca.

Los comentarios al artículo 53.2 del Código Estructural proponen determinar el plazo de descimbrado utilizando la siguiente expresión, basada en el concepto de madurez del hormigón (edad equivalente entre dos hormigones dependiente del tiempo y de la temperatura). Esta fórmula solo se aplica a elementos de hormigón armado fabricados con cementos Portland sin adiciones, suponiendo que el endurecimiento se haya realizado en condiciones ordinarias:

donde:

Q es la diferencia entre la carga que actúa en situación de proyecto y la carga que actúa en una determinada fase constructiva

G es la carga que actúa en una determinada fase de construcción (en el momento de descimbrar), incluido el peso propio y la carga transmitida procedente de forjados cimbrados sobre el elemento a estudiar

T es la temperatura media en °C de las máximas y mínimas diarias durante los j días

J es el número de días desde el hormigonado hasta el descimbrado

Esta fórmula ha estado presente en las ediciones de la norma española desde 1973. Ofrece un ajuste que, si bien prioriza la seguridad, proporciona valores adecuadamente precisos. Además, considera tanto la influencia de la temperatura como la relación entre las cargas. De hecho, representa una simplificación de un enfoque más amplio que se encuentra en la Instrucción HA 61.

Si analizamos la fórmula a una temperatura de 20 °C y consideramos la carga total como la que actúa al descimbrar, obtendremos un valor de 28 días. Conforme aumenta la relación entre la carga que actuará posteriormente y la carga que actuará al descimbrar, la fórmula arroja edades de descimbrado cada vez menores, llegando incluso a valores asintóticos. En consecuencia, esta fórmula produce valores que, si bien pueden inclinarse hacia la seguridad, no generan grandes contradicciones. En la Figura 2 se representa el criterio del Código Estructural para los plazos de descimbrado.

Figura 2. Criterio del Código Estructural de descimbrado

Por ejemplo, supongamos que se quiere estimar el plazo de descimbrado de una estructura atendiendo al método sugerido en los comentarios del artículo 53.2 del Código Estructural. Para ello se considera que se ha empleado en la fabricación del hormigón un cemento Portland y el endurecimiento se ha realizado en condiciones ordinarias. Se supone que la carga que actúa en el momento de descimbrar (incluido el peso propio) es de 45 kN y que la carga total que actuará posteriormente es de 65 kN. Suponemos una temperatura media hasta el descimbrado de 18 °C. En este caso, Q = 65-45 = 20 kN; G = 45 kN. El plazo es j = 15,13 días. Por tanto, se podría descimbrar a los 16 días del hormigonado.

Ahora os presentamos un nomograma elaborado junto con el profesor Pedro Martínez-Pagán. Este recurso puede ser valioso para calcular rápidamente el tiempo de descimbrado en función de la temperatura y la relación Q/G. Por ejemplo, de un vistazo se puede determinar el tiempo necesario para el descimbrado en invierno, a 5 °C.

Referencias:

CALAVERA, J. et al. (2004). Ejecución y control de estructuras de hormigón. Intemac, Madrid, 937 pp.

DÍAZ-LOZANO, J. (2008). Criterios técnicos para el descimbrado de estructuras de hormigón. Tesis doctoral. Departamento de ingeniería civil: construcción. Universidad Politécnica de Madrid.

GASCH, I. (2012). Estudio de la evolución de cargas en forjados y estructuras auxiliares de apuntalamiento durante la construcción de edificios de hormigón in situ mediante procesos de cimbrado, clareado y descimbrado de plantas sucesivas. Tesis doctoral. Departamento de Ingeniería de la Construcción y Proyectos de Ingeniería Civil. Universitat Politècnica de València.

MARTÍ, J.V.; YEPES, V.; GONZÁLEZ, F. (2014). Fabricación, transporte y colocación del hormigón. Apuntes de la Universitat Politècnica de València, 189 pp.

Cursos:

Curso de estructuras auxiliares en la construcción: andamios, apeos, entibaciones, encofrados y cimbras.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Comunicaciones presentadas al 27th International Congress on Project Management and Engineering AEIPRO 2023

Durante los días 10-13 de julio de 2023 tiene lugar en Donostia-San Sebastián (Spain) el 27th International Congress on Project Management and Engineering AEIPRO 2023. Es una buena oportunidad para debatir y conocer propuestas sobre dirección e ingeniería de proyectos. Nuestro grupo de investigación, dentro del proyecto de investigación HYDELIFE, presenta varias comunicaciones. A continuación os paso los resúmenes.

BRUN-IZQUIERDO, A.; YEPES-BELLVER, L.; ALCALÁ, J.; YEPES, V. (2023). Optimización energética de tableros tipo losa pretensados aligerados mediante modelos Kriging. 27th International Congress on Project Management and Engineering, AEIPRO, 10-13 de julio, Donostia/San Sebastián (Spain).

El objetivo de este trabajo es desarrollar una metodología para optimizar la energía en la construcción de tableros losa pretensado aligerados. Se lleva a cabo un análisis de la sección transversal para determinar los parámetros de diseño a través de un estudio del estado del arte. A partir de ese análisis, se identifican las variables de diseño que mejorarán la eficiencia energética del tablero. La metodología se divide en dos fases: primero, se utiliza una técnica estadística llamada hipercubo latino para muestrear las variables del tablero y determinar una superficie de respuesta; y en segundo lugar, se optimiza la superficie de respuesta mediante un modelo de optimización basado en Kriging. Como resultado, se ha desarrollado una metodología que reduce el costo energético en la construcción de tableros losa pretensado aligerados. Las recomendaciones para mejorar la eficiencia energética incluyen emplear esbelteces elevadas (alrededor de 1/28), reducir el consumo de hormigón y armadura activa, y aumentar la cantidad de armadura pasiva.

HADIZADEH-BAZAZ, M.; NAVARRO, I.J.; YEPES, V. (2023). Durability assessment and re-design of coastal concrete bridge through a non-destructive damage detection method. 27th International Congress on Project Management and Engineering, AEIPRO, 10-13 de julio, Donostia/San Sebastián (Spain).

Los expertos y los gobiernos llevan tiempo centrándose en reducir los costes de reparación y mantenimiento de estructuras cruciales como los puentes mediante un mantenimiento y una reparación continuos. Este estudio explora la rentabilidad de dos métodos de predicción de daños mediante el método de densidad espectral de potencia (PSD) en comparación con el método convencional de detección de daños mediante el rediseño de diferentes espesores de recubrimiento de hormigón para un puente costero de hormigón armado. El estudio evalúa el impacto de los iones cloruro en la localización y extensión de los daños a lo largo de la vida útil del puente y compara los costes totales de mantenimiento y reparación. Los resultados muestran que, si bien el método PSD es eficaz para estructuras de hormigón con recubrimientos de hormigón bajos, el aumento del espesor del recubrimiento de hormigón puede dar lugar a mayores costes de reparación.

YEPES, V.; MARTÍNEZ-PAGÁN, P.; ROSCHIER, L.; BOULET, D.J.; BLIGHT, T. (2023). Códigos abiertos basados en Python para la construcción de nomogramas y su aplicación en la ingeniería de proyectos. 27th International Congress on Project Management and Engineering, AEIPRO, 10-13 de julio, Donostia/San Sebastián (Spain).

La Nomografía es una disciplina científica que se encarga de representar gráficamente fórmulas complejas mediante nomogramas, permitiendo el cálculo de tres o más variables matemáticas. Durante el siglo XX, esta técnica fue ampliamente utilizada en áreas como la ingeniería, medicina, electrónica, ciencias físicas, biológicas, etc. Sin embargo, con la llegada de las calculadoras y computadoras, la construcción de nuevos nomogramas y su enseñanza en la universidad disminuyeron. En los últimos años, la nomografía ha resurgido gracias a la ayuda de códigos de programación como PyNomo y Nomogen, basados en Python, que pueden generar un nomograma en cuestión de segundos, frente a las horas que antes requerían. En este trabajo se presentan estos códigos abiertos y algunos nomogramas generados con ellos, analizando su usabilidad, precisión y contribución a la relación entre las variables de las expresiones matemáticas. Finalmente, se destacan las posibilidades del uso de los nomogramas en la enseñanza e ingeniería de proyectos.

Nomogramas para su empleo en trabajos de movimiento de tierras

Este artículo presenta cinco nomogramas originales que pueden ser utilizados en proyectos de movimientos de tierra. El primero de ellos calcula el peso específico aparente de un suelo, mientras que el segundo nomograma facilita el valor de la piedra en el diseño de voladuras según la metodología de Ash. Los dos siguientes se aplican para determinar la capacidad de la hoja empujadora de un buldócer, y finalmente, el último nomograma ayuda a calcular el rendimiento de escarificado de un buldócer.

Estos nomogramas demuestran también las capacidades de los programas de código abierto, PyNomo y Nomogen, para generar nomogramas adaptados a las necesidades de cálculo de cualquier proyectista. Este proyecto es el resultado de una colaboración internacional entre profesores de Finlandia, Canadá y Australia, y su artículo ha sido publicado en la revista inGEOpress en mayo de 2023.

En este trabajo se proporcionan cinco nomogramas originales generados con el programa Pynomo (http://lefakkomies.github.io/pynomo-doc/introduction/introduction.html), muy útiles para su empleo en trabajos de obra civil, movimiento de tierras y/o minería, así como en ámbito docente. Los ejemplos resueltos por cada uno de los nomogramas también demuestran que los valores obtenidos se obtienen con una precisión adecuada a los requerimientos que se exigen en ingeniería de proyectos, haciéndolos útiles cuando no se tiene acceso a ordenadores o a calculadoras programables y, especialmente, en el manejo de ecuaciones cuyo empleo sea repetitivo.

Referencia:

MARTÍNEZ-PAGÁN, P.; YEPES, V.; ROSCHIER, L.; BOULET, D.; BLIGHT, T. (2023). Nomogramas para su empleo en trabajos de movimiento de tierras. Canteras y explotaciones, 657(3):44-48.

Os paso a continuación el artículo entero por si os resulta de interés.

Descargar (PDF, 3.41MB)

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Códigos abiertos para la elaboración de nomogramas en el ámbito de la ingeniería civil y minera

En este artículo se hace una introducción sobre los códigos abiertos, PyNomo y Nomogen, para la elaboración de nomogramas o ábacos de útil aplicación en el ámbito de la ingeniería civil y minera, resolviendo de forma gráfica y eficiente ecuaciones comúnmente utilizadas y sin necesidad de realizar cálculos manuales exhaustivos. Se presentan varios ejemplos de nomogramas realizados con PyNomo y Nomogen que servirán para mostrar la utilidad de estos códigos abiertos en el campo de la ingeniería hidráulica. Se trata de una colaboración internacional con profesores de Finlandia, Canadá y Australia, cuyo resultado se ha publicado en la revista inGEOpress, en su número de abril del 2023.

La nomografía se puede definir como aquella rama de las matemáticas que se encarga de la representación gráfica de ecuaciones a través de nomogramas (también conocidos como ábacos) que permiten poner en relación tres o más variables resolviendo una de ellas cuando se conocen el resto. Esta área de las matemáticas fue implantada en 1880, y posteriormente desarrollada por Maurice d’Ocagne. El empleo de la nomografía tuvo su mayor desarrollo en el siglo pasado como una forma de resolver de forma rápida y precisa complejas expresiones matemáticas en sectores tan diversos como medicina, aeronáutica, hidráulica, química, física, matemáticas, electrónica, radio, balística, alimentación, etc. Por ello, son innumerables los ejemplos que han llegado hasta nuestros días y que aún aparecen en libros especializados de ingeniería, especialmente hidráulica, ingeniería civil, minería, etc. . Además, en la actualidad, todavía es común que un gran volumen de documentación técnica, folletos de especificaciones técnicas y catálogos de equipos faciliten el cálculo de numerosas expresiones a través de nomogramas.

Referencia:

MARTÍNEZ-PAGÁN, P.; YEPES, V.; ROSCHIER, L.; BOULET, D.; BLIGHT, T. (2023). Introducción de los códigos abiertos PyNomo y Nomogen para la elaboración de nomogramas en el ámbito de la ingeniería civil y minera. Ingeopres, 302:66-70.

Os paso a continuación el artículo entero por si os resulta de interés.

Descargar (PDF, 2.76MB)

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Nomograma para el cálculo de la producción del ripado y transporte con un buldócer

Figura 1. Buldócer Cat D9T. https://commons.wikimedia.org/wiki/File:CatD9T.jpg

Uno de los ejemplos usuales es la producción de un buldócer (bulldozer, en inglés), que primero debe escarificar un terreno y luego debe empujarlo hasta una distancia de transporte determinada. En una entrada anterior dimos la resolución de la producción combinada de un buldócer.

Ahora os presentamos un nomograma elaborado junto con el profesor Pedro Martínez-Pagán sobre la producción del ripado y transporte con dicha máquina. Se han seguido las recomendaciones empíricas recogidas en el “Manual de arranque, carga y transporte en minería de cielo abierto” (Gómez de las Heras et al., 1995).

A continuación os voy a dar resuelto un problema de este tipo. Se trata de uno de los muchos casos que explicamos en el Curso de gestión de costes y producción de la maquinaria empleada en la construcción. Os animo a que, si estáis interesados, os informéis de este curso en línea.

Descargar (PDF, 1.17MB)

Referencias:

GÓMEZ DE LAS HERAS, J.; MANGLANO, S.; TOLEDO, J.; LÓPEZ-JIMENO, C.; LÓPEZ-JIMENO, E. (1995). Manual de arranque, carga y transporte en minería a cielo abierto. Instituto Geológico y Minero de España, Madrid, 604 pp.

YEPES, V. (1995). Maquinaria de movimiento de tierras. Servicio de Publicaciones de la Universidad Politécnica de Valencia. SP.UPV-264. 144 pp.

YEPES, V. (1997). Equipos de movimiento de tierras y compactación. Problemas resueltos. Colección Libro Docente n.º 97.439. Ed. Universitat Politècnica de València. 256 pág. Depósito Legal: V-4598-1997. ISBN: 84-7721-551-0.

Curso:

Curso de gestión de costes y producción de la maquinaria empleada en la construcción

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Nomograma para el cálculo del peso específico aparente de un suelo

El “peso específico de un suelo“, como relación entre el peso y su volumen, es un valor dependiente de la humedad, de los huecos de aire y del peso específico de las partículas sólidas. Para evitar confusiones, las determinaciones de los ensayos de laboratorio facilitan, por un lado, el “peso específico seco” y por otro la humedad. El peso específico natural de un suelo granular suele variar entre 12 y 25 kN/m³, de 14 a 25 kN/m³ en suelos finos y de 1 a 10 kN/m³ en suelos orgánicos. El peso específico seco de un suelo suele variar entre 18 y 27 kN/m³ en arcillas y entre 14 y 18 kN/m³ en suelos granulares. Es importante tener en cuenta que estos valores son solo una guía general y pueden variar dependiendo de las características específicas del suelo y las condiciones ambientales.

Además, presentamos un nomograma original elaborado en colaboración con el profesor Pedro Martínez-Pagán y un ejercicio resuelto donde se demuestra la relación entre el peso específico aparente de un suelo en función de su humedad, el índice de huecos y el peso específico de las partículas sólidas. Espero que esta información sea de vuestro interés.

Descargar (PDF, 948KB)

Referencias:

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Nomograma para el cálculo del radio hidráulico de una sección trapecial

En un artículo previo, explicamos cómo calcular el radio hidráulico para diferentes secciones. A continuación presentamos un ejercicio resuelto para el caso de una sección trapecial.

Además, presentamos un nomograma original elaborado en colaboración con los profesores Daniel Boulet, Matías Raja y Pedro Martínez-Pagán. En este nomograma se puede utilizar cualquier unidad para las longitudes. Espero que esta información sea de vuestro interés.

Descargar (PDF, 375KB)

Referencias:

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Nomograma para el cálculo del radio hidráulico de una sección circular

En un artículo previo, explicamos cómo calcular el radio hidráulico para diferentes secciones. Sin embargo, en el caso de una sección circular, el uso de un nomograma es más conveniente, pues evita el cálculo intermedio del ángulo del sector circular que abarca el agua.

Además, el empleo de esta resolución gráfica permite visualizar aspectos que son difíciles de deducir directamente de las fórmulas aplicadas. En este caso, el nomograma permite observar que los radios hidráulicos pueden ser iguales para diferentes calados. También permite ver claramente el rango de variación y el valor máximo. Aunque las fórmulas también pueden proporcionar información sobre el valor extremo, es necesario calcular la derivada, igualarla a cero y resolver la ecuación.

A continuación, se presenta un problema resuelto que incluye las ecuaciones utilizadas, el nomograma y un par de gráficas que relacionan el calado normalizado con el diámetro en relación con el ángulo del sector circular y al radio hidráulico normalizado. Además, presentamos un nomograma original elaborado en colaboración con los profesores Daniel Boulet y Pedro Martínez-Pagán. Espero que esta información sea de vuestro interés.

Descargar (PDF, 933KB)

Referencias:

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.