Este trabajo se enmarca dentro del proyecto de investigación RESILIFE, que dirijo como investigador principal, junto con el profesor Julián Alcalá, en la Universitat Politècnica de València. Además, es uno de los resultados de la tesis doctoral de Lorena Yepes.
En cuanto la comunicación esté publicada en el libro de ponencias, os pasaré el enlace para su descarga gratuita. A continuación os paso el resumen de la comunicación presentada.
El artículo «Multi-Attribute Decision-Making in Prestressed Concrete Road Flyover Design», propone una innovadora metodología para optimizar el diseño de puentes de hormigón pretensado teniendo en cuenta simultáneamente tres criterios clave: el coste económico, las emisiones de CO₂ y la energía incorporada en los materiales. Su objetivo es encontrar soluciones de compromiso que equilibren sostenibilidad y eficiencia estructural.
Aportaciones principales del estudio
Este trabajo aporta un enfoque sistemático y práctico para integrar criterios medioambientales y económicos en el diseño de pasos elevados. Frente a las metodologías tradicionales que suelen priorizar únicamente el coste, los autores aplican técnicas de toma de decisiones multicriterio para considerar también el impacto ambiental desde el inicio del proceso proyectual. Además, ofrecen pautas concretas para diseños preliminares que buscan un equilibrio entre coste, emisiones y consumo energético.
Metodología empleada
La investigación se basa en técnicas avanzadas de optimización y modelado. En primer lugar, se utilizaron 50 soluciones iniciales de diseño generadas mediante un muestreo estadístico conocido como Latin Hypercube Sampling, que explora diferentes combinaciones de parámetros como la resistencia del hormigón, la anchura de la base y la profundidad del tablero.
A continuación, se aplicó un modelo de sustitución de tipo Kriging, capaz de estimar con gran precisión los resultados estructurales sin necesidad de cálculos exhaustivos para cada diseño. Esto permitió ampliar el análisis a 1.000 soluciones adicionales simuladas.
Con todas las alternativas sobre la mesa, se extrajo la “frontera de Pareto”, un conjunto de soluciones no dominadas que representan los mejores compromisos posibles entre los tres objetivos. Finalmente, se aplicaron distintos escenarios de toma de decisiones multiatributo, asignando diferentes pesos a cada criterio, para seleccionar los diseños más equilibrados.
Resultados más relevantes
El análisis reveló que los diseños más sostenibles tienen características comunes: una relación entre canto del tablero y luz principal cercana a 1/30 y una resistencia del hormigón de 40 MPa. Estas configuraciones permiten reducir tanto el consumo de materiales como las emisiones sin comprometer la viabilidad estructural.
Dependiendo del peso asignado a cada criterio (coste, emisiones, energía), se identificaron varias soluciones óptimas, destacando especialmente dos (denominadas #6 y #13) por su buen rendimiento integral. Curiosamente, priorizar solo el coste lleva a soluciones con mayor canto, mientras que priorizar el medio ambiente genera estructuras más esbeltas y materialmente eficientes.
Conclusiones y recomendaciones
El estudio concluye que aplicar técnicas de decisión multicriterio en la ingeniería civil permite diseñar infraestructuras más sostenibles y racionales, sin sacrificar funcionalidad ni economía. Se recomienda considerar desde fases tempranas del diseño variables ambientales clave como las emisiones o la energía embebida, además de los costes.
Asimismo, los autores sugieren incorporar la participación de los diferentes agentes implicados (ingenieros, administraciones, ciudadanía) para lograr soluciones más equilibradas y duraderas.
Este trabajo representa un avance hacia una práctica de la ingeniería más alineada con los Objetivos de Desarrollo Sostenible, y especialmente con el ODS 9, que promueve infraestructuras resilientes, sostenibles e innovadoras.
Referencia:
YEPES-BELLVER, L.; ALCALÁ, J.; YEPES, V. (2025). Multi-attribute decision-making in prestressed concrete road flyover design. International Conference on High Performance and Optimum Design of Structures and Materials, HPSM/OPTI 2025, 10-12 June 2025, Edinburgh, UK.
De izquierda a derecha: Julián Alcalá, Salvador Ivorra, Lorena Yepes, Tatiana García y Antonio Tomás.
Hoy, 6 de junio de 2025, ha tenido lugar la defensa de la tesis doctoral de Dª. Lorena Yepes Bellver, titulada “Multi-criteria optimization for sustainable design of post-tensioned concrete slab bridges using metamodels”, dirigida por el profesor Julián Alcalá González. La tesis ha obtenido la máxima calificación de sobresaliente «cum laude». A continuación, presentamos un pequeño resumen de la misma.
Esta tesis utiliza técnicas de modelización sustitutiva para optimizar los costes económicos y medioambientales en puentes losa de hormigón postesado hormigonado in situ. El objetivo principal de esta investigación es desarrollar una metodología sistemática que permita optimizar el diseño de puentes, reduciendo los costes, las emisiones de CO₂ y la energía necesaria para construir este tipo de puentes sin comprometer la viabilidad estructural o económica. El marco de optimización propuesto consta de dos fases secuenciales: la primera se centra en ampliar el espacio de búsqueda y la segunda intensifica la búsqueda de soluciones óptimas. El metamodelo basado en Kriging realiza una optimización heurística que da como resultado un diseño con emisiones de CO₂ significativamente menores que los diseños convencionales. El estudio revela que una relación de esbeltez de aproximadamente 1/30 arroja resultados óptimos, ya que se reduce el consumo de material y se mantiene la integridad estructural. Además, el aumento de la armadura pasiva compensa la reducción de hormigón y armadura activa, lo que da como resultado un diseño más sostenible. Por otra parte, se identifica una compensación entre costes y emisiones que muestra que un modesto aumento de los costes de construcción (menos del 1 %) puede reducir sustancialmente las emisiones de CO₂ (más del 2 %), lo que demuestra que el diseño de puentes sostenibles puede ser económicamente viable.
La investigación explora más a fondo la optimización de la energía incorporada en la construcción de pasos elevados de carreteras anuladas mediante el uso de muestreo por hipercubo latino y optimización basada en Kriging. La metodología permite identificar los parámetros críticos de diseño, como los altos coeficientes de esbeltez (en torno a 1/28), el uso mínimo de hormigón y armadura activa, y el aumento de la armadura pasiva para mejorar la eficiencia energética. Aunque en el estudio se emplearon Kriging y redes neuronales artificiales (RNA), Kriging demostró ser más eficaz a la hora de identificar óptimos locales, a pesar de que las redes neuronales ofrecen predicciones absolutas más precisas. Esto pone de manifiesto la eficacia de los modelos sustitutos a la hora de orientar las decisiones de diseño sostenible, incluso cuando los modelos no ofrecen predicciones absolutas perfectamente exactas.
En el contexto de la optimización de costes para puentes de losa postesada, el estudio demuestra el potencial del modelado sustitutivo combinado con la simulación del recocido. Los resultados muestran que el método de optimización basado en Kriging conduce a una reducción de costes del 6,54 %, principalmente mediante la minimización del uso de materiales, concretamente de hormigón en un 14,8 % y de acero activo en un 11,25 %. Estas reducciones en el consumo de material se consiguen manteniendo la integridad estructural y la capacidad de servicio del puente, lo que convierte al modelado sustitutivo en una herramienta práctica y eficaz para la optimización económica en el diseño de puentes.
El estudio también evalúa la forma de optimizar las emisiones de CO₂ en pasos elevados de carreteras pretensadas. Se identifican los parámetros óptimos de diseño, como grados de hormigón entre C-35 y C-40 MPa, profundidades del tablero entre 1,10 y 1,30 m, y anchuras de base entre 3,20 y 3,80 m. La red neuronal mostró las predicciones más precisas entre los modelos predictivos analizados, con los errores medios absolutos (MAE) y cuadrados medios (RMSE) más bajos. Estos resultados subrayan la importancia de seleccionar el modelo predictivo adecuado para optimizar las emisiones de CO₂ en el diseño de puentes y destacan el valor de utilizar modelos sustitutivos para mejorar la sostenibilidad en los proyectos de ingeniería civil.
Por último, la investigación integra la toma de decisiones multicriterio (MCDM) con la optimización basada en Kriging para evaluar y optimizar los diseños de puentes en relación con objetivos económicos, medioambientales y estructurales. El enfoque MCDM permite evaluar de manera más exhaustiva las alternativas de diseño al tener en cuenta las compensaciones entre coste, impacto ambiental y rendimiento estructural. Esta integración contribuye al desarrollo sostenible de las infraestructuras, ya que facilita la selección de diseños óptimos que se ajusten a los objetivos de sostenibilidad.
En conclusión, esta tesis demuestra que el modelado sustitutivo, que utiliza explícitamente el Kriging y redes neuronales artificiales, es un enfoque práctico para optimizar las dimensiones medioambiental y económica del diseño de puentes. El marco de optimización en dos fases que aquí se presenta proporciona una metodología eficiente desde el punto de vista computacional que permite identificar soluciones de diseño óptimas y sostenibles que cumplen las restricciones estructurales y económicas. Los resultados sugieren que la metodología es aplicable a proyectos de infraestructuras a gran escala y sentarán las bases para futuras investigaciones. Futuros estudios podrían investigar el uso de algoritmos y modelos de optimización adicionales para perfeccionar aún más el proceso de optimización y mejorar la aplicabilidad de estas metodologías en proyectos reales.
En España, las Escuelas de Ingeniería y Arquitectura ofrecen títulos universitarios habilitantes para ejercer profesiones reguladas en sectores fundamentales como la arquitectura, la medicina y la ingeniería. Este modelo formativo no solo tiene como objetivo proporcionar una sólida base teórica, sino también formar profesionales competentes para afrontar los retos del mundo laboral. Las Escuelas de Ingenieros de Caminos, Canales y Puertos ejemplifican la estrecha vinculación entre la docencia y la práctica profesional, siendo históricamente referentes gracias a sus catedráticos, quienes han combinado la labor académica con la ejecución de importantes proyectos de infraestructura.
Historia y vínculo con la práctica profesional
Desde sus inicios —como la Escuela de Ingenieros de Caminos de Madrid, fundada en 1802— estas instituciones han contado con profesores de reconocido prestigio internacional que han liderado y gestionado obras de gran envergadura (puentes, presas y puertos, entre otras). La experiencia directa acumulada en el campo aporta un valor añadido incalculable, ya que permite a los egresados no solo dominar la teoría, sino también comprender y aplicar soluciones reales a los desafíos técnicos y constructivos. La integración de la práctica profesional en la enseñanza resalta la inseparabilidad entre ciencia y técnica, base imprescindible para la formación completa del ingeniero.
Limitaciones del modelo universitario actual
El sistema universitario vigente ha privilegiado el desarrollo de la carrera investigadora y académica, orientando a estudiantes brillantes hacia el doctorado, contratos predoctorales, estancias de investigación y la promoción en el escalafón universitario. Si bien este enfoque es fundamental para el avance científico, en el ámbito de la ingeniería ha llevado a descuidar la incorporación de conocimientos derivados de la experiencia práctica de alto nivel. En las últimas décadas, se ha reducido drásticamente la presencia de profesores con una sólida trayectoria profesional en la dirección de grandes obras, lo que genera una desconexión entre el conocimiento teórico y las habilidades prácticas necesarias en el ejercicio profesional.
La figura del profesor asociado
Se ha sugerido que la figura del profesor asociado podría compensar la carencia de profesionales con experiencia práctica en el claustro universitario. No obstante, este modelo presenta áreas de mejora, ya que dichos profesionales, aunque compaginan la actividad práctica con la docencia, tienen contratos que impiden desarrollar, a largo plazo, una carrera académica estable y sólida. Esta situación limita su participación en procesos de investigación y en la toma de decisiones estratégicas a largo plazo, mermando la transferencia directa de conocimientos prácticos a las nuevas generaciones.
La necesidad de integrar la experiencia profesional en la academia
La ausencia de expertos con amplia experiencia en grandes proyectos de ingeniería repercute directamente en la formación de los estudiantes, quienes terminan sus estudios con un conocimiento teórico destacado, pero con habilidades y experiencia práctica mejorables para su incorporación en el mercado laboral. Esta limitación dificulta la transición profesional, pues las empresas y organismos demandan ingenieros capaces de aplicar sus conocimientos en la ejecución y gestión de obras complejas. Ante esta situación, resulta imperativo revisar los criterios de evaluación del profesorado universitario, de manera que la Agencia Nacional de Evaluación de la Calidad y Acreditación (ANECA) reconozca y valore especialmente la experiencia profesional de calidad al evaluar a este tipo de docentes.
Propuesta para la integración de profesionales en el ámbito universitario
Para solventar la brecha entre la formación teórica y la práctica profesional, se plantea la necesidad de crear nuevas vías de incorporación de profesionales con amplia experiencia en el ejercicio de la ingeniería al ámbito académico. Estas nuevas estructuras permitirían a dichos profesionales desarrollar una carrera académica paralela, estable y digna, sin renunciar a su actividad práctica. Resulta fundamental que esta reforma venga acompañada de una modificación en los criterios de evaluación de las instituciones, integrando los méritos derivados de la experiencia profesional junto a la excelencia investigadora. Modelos internacionales —como los desarrollados en Alemania, Canadá y Suiza— demuestran que es factible conciliar la actividad profesional y académica de manera efectiva, facilitando una mayor transferencia de conocimientos prácticos a los estudiantes y mejorando la conexión entre la formación y las necesidades del mercado laboral.
Conclusión y propuesta de acción
España no puede seguir anclada en un modelo educativo que excluya a aquellos profesionales que cuentan con la experiencia práctica necesaria para enriquecer la formación de los ingenieros. Es urgente la realización de una reforma que integre la experiencia profesional en la valoración del profesorado universitario, garantizando así una educación completa que responda a las exigencias del siglo XXI. En este sentido, se debería revisar en profundidad los criterios de evaluación del profesorado en la docencia de las profesiones reguladas y alcanzar un acuerdo que permita la incorporación efectiva de profesionales con trayectoria en la docencia y la investigación.
Josef Melan (1854–1941). https://jam.jihlava.cz/en/architect/3-josef-melan
Josef Melan fue un ingeniero austríaco ampliamente reconocido por su destacado papel en el desarrollo de la construcción de puentes de hormigón armado a finales del siglo XIX. Se le acredita la invención del Sistema Melan, un método innovador para la construcción de puentes reforzados. A diferencia de los enfoques previos, su sistema no incorporaba barras de hierro dentro de la estructura de hormigón armado, sino que empleaba arcos de celosía rígidos de hierro como elemento de refuerzo.
En 1898, Melan alcanzó un reconocimiento significativo tras la construcción de un puente de 42,4 m de luz en Steyr, caracterizado por un arco de altura reducida. En su momento, esta obra representó el mayor puente de hormigón armado a nivel mundial. Entre sus proyectos más notables se encuentra el Puente del Dragón en Liubliana, una de las primeras estructuras de gran escala en emplear su innovador sistema constructivo.
Nacido el 18 de noviembre de 1853 en Viena, entonces parte del Imperio austrohúngaro, Melan falleció el 6 de febrero de 1941 en Praga, en la anterior Checoslovaquia. Inició sus estudios de ingeniería civil en la Universidad Técnica de Viena en 1869 y los completó en 1874. Posteriormente, tras su graduación, se desempeñó como asistente de Emil Winkler en la cátedra de Ingeniería Ferroviaria y Construcción de Puentes, marcando así el inicio de su destacada trayectoria académica y profesional.
En 1880, presentó su tesis de habilitación sobre la teoría de puentes y ferrocarriles en la misma universidad, donde ejerció como docente hasta 1886. Durante este período, además de su labor académica, desarrolló actividades profesionales en los departamentos de diseño de la empresa de construcción de puentes Ignaz Gridl y junto al contratista Gaertner, ambos con sede en Viena. En 1880, fue nombrado profesor asociado de mecánica estructural y estática gráfica en la Universidad Técnica Alemana de Brno, y en 1890 ascendió a catedrático en la misma especialidad. Posteriormente, en 1895, asumió la Cátedra de Construcción de Puentes, y en 1902 pasó a ocupar el mismo cargo en la Universidad Técnica Alemana de Praga (fundada en 1717), donde trabajó hasta su jubilación en 1923.
Durante su estancia en Viena, Melan inició el desarrollo de cálculos relacionados con la deformación estática en grandes puentes colgantes, con el propósito de optimizar su diseño y reducir costes. En 1888, Melan publicó los resultados de sus investigaciones, lo que atrajo la atención de su antiguo compañero de estudios, Gustav Lindenthal, quien le encargó la revisión estructural del Williamsburg Bridge de Nueva York, el puente colgante más grande del mundo en aquella época.
Paralelamente, ese mismo año, el ingeniero Victor Brausewetter, en colaboración con el fabricante de cemento Adolf Pittel, fundó la empresa Pittel & Brausewetter y promovió la creación de una asociación dedicada a la realización de ensayos comparativos de carga sobre estructuras abovedadas. Estos ensayos abarcaban desde bóvedas de fábrica en hormigón simple hasta elementos de hormigón armado. Desde 1886, la empresa de Gustav Adolf Waysse ya había construido estructuras basadas en la patente de Joseph Monier, con refuerzo de malla de acero en ambas direcciones. No obstante, tras un exhaustivo análisis de los ensayos mencionados, Melan expresó su escepticismo respecto al sistema, manifestando reservas en cuanto a la resistencia de los alambres empleados.
En 1892, presentó su propio y revolucionario sistema estructural, basado en un refuerzo longitudinal rígido para bóvedas, que sentó las bases de la arquitectura moderna. Para estructuras de menor luz, se utilizaron vigas en L dobladas, mientras que para las de mayor envergadura se emplearon cerchas metálicas. Gracias a su mayor capacidad portante, este método fue rápidamente adoptado en la construcción de techos en almacenes, fábricas y grandes naves industriales. Una innovación notable fue la posibilidad de suspender el encofrado del propio refuerzo y hormigonar los arcos sin necesidad de cimbras de anillos. Pittel & Brausewetter realizó pruebas de este sistema entre 1893 y 1895 en edificaciones de menor escala, aunque lamentablemente ninguna de ellas ha perdurado hasta nuestros días.
Uno de sus discípulos, Fritz Emperger, desempeñó un papel fundamental en la difusión del método de Melan. En 1893, fundó en la ciudad de Nueva York la Melan Arch Construction Company, que en 1894 se encargó del diseño y la construcción de dos puentes en Rock Rapids (Iowa) y Cincinnati (Ohio). Antes de que finalizara el siglo, su empresa había construido veintisiete puentes más, entre ellos el puente sobre el río Kansas en Topeka (Kansas), edificado entre 1896 y 1897, con cinco arcos de 30 metros de luz cada uno.
A pesar del éxito de su sistema en Estados Unidos, la comunidad técnica europea mantuvo una actitud escéptica hasta que Melan diseñó en 1896 un puente en Steyr, construido bajo la supervisión de Victor Brausewetter en 1898. Esta estructura, ubicada en la ciudad de Steyr, Alta Austria, cruzaba un brazo del río homónimo mediante un arco de tres vanos, con una luz máxima de 42,4 m y una flecha extremadamente reducida de 1:16. Ese mismo año, Melan diseñó lo que probablemente sea el puente de hormigón armado más antiguo de las tierras checas, ubicado en Veveří, cuyo diseño se inspiró en el puente medieval original que cruzaba el foso del castillo. En 1901 se finalizó la construcción del Puente del Dragón de Liubliana, cuya estructura de hormigón visto combinada con revestimientos de bronce fue diseñada por el arquitecto dálmata Jurij Zaninović.
Puente del Dragón, en Liubliana. Imagen: V. Yepes (2018)
Simultáneamente, Melan resultó adjudicatario de un concurso público para el diseño de un puente vial en Lausana, destinado a conectar los distritos de Chauderon y Montbenon. Posteriormente, en 1912, Melan proyectó un puente de hormigón armado en Le Sépey, ubicado en el sur de Suiza.
Su labor académica en Praga tuvo un impacto significativo en el desarrollo de la oficina técnica de Pittel & Brausewetter, que se convirtió en un centro de formación para sus estudiantes. Entre 1908 y 1912, Konrad Kluge (1878-1945), uno de sus alumnos más distinguidos, diseñó varios puentes con arcos rígidos reforzados con vigas en L, ubicados en Debrny, Jihlava, Přísečnice (hoy desaparecida), česká Třebová y Oloví.
En 1920, recibió el título de doctor honoris causa de la Escuela Técnica Superior de Aquisgrán en reconocimiento a su labor como profesor y científico en el campo de la ingeniería de puentes, así como por sus avances como inventor de un nuevo tipo de puente de hormigón armado.
A pesar de su avanzada edad, Melan mantuvo una constante actividad profesional. En julio de 1928, Melan diseñó un puente de arco metálico en Ústí nad Labem, basado en una propuesta de Ernst Krob, director de la Autoridad de Construcción de la ciudad. La construcción de la obra se llevó a cabo entre 1934 y 1936, consolidando de este modo su legado en el ámbito de la ingeniería estructural.
Melan se erigió como una de las figuras más influyentes en la teoría y práctica de la construcción de puentes en Austria durante la transición desde la fase de formación disciplinar hasta el período de consolidación de la teoría de estructuras. Su innovación más destacada, el Sistema Melan, introdujo una metodología pionera que combinaba de manera innovadora acero y hormigón en la construcción de puentes. A partir de la década de 1890, este sistema fue ampliamente aceptado en Europa y Estados Unidos, posicionándose como una de las soluciones constructivas más avanzadas de su época. Su impacto fue reconocido con la medalla de oro en la Exposición Universal de París en 1900.
En 1893, Melan publicó sus estudios sobre arcos de hormigón reforzado con estructuras de hierro, lo que marcó un hito en la construcción mixta. Su prestigio internacional experimentó un notable incremento en 1898, con la construcción de un puente de 42,4 m de luz en Steyr, considerado el puente de hormigón armado más extenso de su época. En este caso, el arco metálico inicial se ejecutó mediante voladizos sucesivos con un atirantamiento provisional.
Más allá de sus aportes en la construcción mixta, Melan dejó una huella indeleble en la ingeniería de puentes metálicos. En 1888, Melan fue pionero en cuantificar los efectos de la teoría de segundo orden, un avance crucial en la modelización estructural. Sus tratados sobre puentes recibieron un reconocimiento internacional destacado, y en 1913, su obra sobre puentes en arco y colgantes fue traducida al inglés por el ingeniero estadounidense David B. Steinman.
Además de su labor teórica, Melan ejerció una influencia decisiva en el desarrollo de la ingeniería de grandes puentes en Estados Unidos. Colaboró con el Departamento de Puentes de Nueva York en la verificación de los cálculos del Williams Bridge y en la evaluación del Hell Gate Bridge, diseñado por la oficina del ingeniero Gustav Lindenthal. Su impacto en la construcción de puentes en Estados Unidos durante las dos primeras décadas del siglo XX fue sin precedentes.
Principales contribuciones a la teoría de estructuras
Josef Melan realizó importantes aportaciones a la teoría de estructuras a lo largo de su carrera, plasmadas en diversas publicaciones de referencia. Entre sus primeros trabajos destacan Beitrag zur Berechnung eiserner Hallen-Gespärre (1883), en el que abordó el cálculo de cerchas metálicas en naves industriales, y Ueber den Einfluss der Wärme auf elastische Systeme (1883), donde analizó los efectos térmicos en sistemas elásticos. Posteriormente, en Beitrag zur Berechnung statisch unbestimmter Stabsysteme (1884), se centró en la resolución de sistemas de barras estáticamente indeterminados.
Su obra Theorie der eisernen Bogenbrücken und der Hängebrücken (1888) estableció las bases para el diseño de puentes en arco de hierro y puentes colgantes, consolidando su prestigio en la ingeniería estructural. Años más tarde, en Theorie des Gewölbes und des Eisenbetongewölbes im besonderen (1908), amplió su estudio al análisis de bóvedas, con especial énfasis en las estructuras de hormigón armado.
Durante su etapa en la Universidad Técnica Alemana de Praga, Melan publicó Der Brückenbau, una serie de volúmenes basados en sus conferencias impartidas entre 1910 y 1917. Su influencia trascendió el ámbito europeo con la publicación en inglés de Theory of Arches and Suspension Bridges (1913) y Plain and Reinforced Concrete Arches (1915), obras que consolidaron su impacto en la ingeniería de puentes a nivel internacional.
Acaban de publicar nuestro artículo en la revista Infrastructures, indexada en el JCR. El estudio presenta una metodología de optimización de costes para puentes losa aligerados postesados mediante metamodelos, en la que se destaca la aplicación del modelo Kriging en combinación con algoritmos heurísticos.
Este trabajo se enmarca dentro del proyecto de investigación RESILIFE, que dirijo como investigador principal, junto con el profesor Julián Alcalá, en la Universitat Politècnica de València. A continuación, explicamos brevemente el contenido del artículo que podéis descargar gratuitamente.
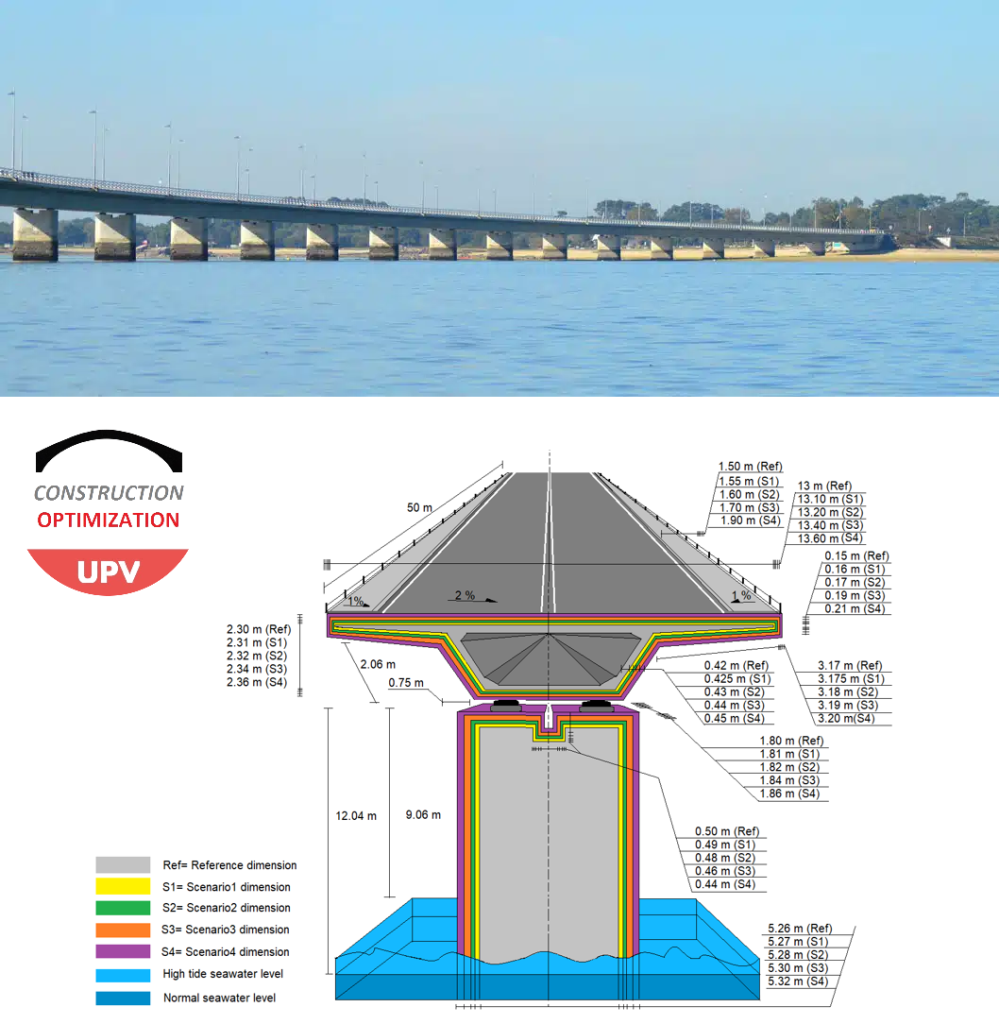
La investigación se centra en un puente de tres vanos con luces de 24, 34 y 28 m, y optimiza el diseño estructural para reducir costes sin comprometer los criterios de servicio y seguridad. Se identifica una reducción del 6,54 % en los costes en comparación con enfoques tradicionales, lograda principalmente mediante la disminución del uso de hormigón en un 14,8 % y del pretensado en un 11,25 %.
El trabajo también evalúa distintas técnicas predictivas, como redes neuronales y funciones de base radial, y determina que las redes neuronales presentan el menor error de predicción, aunque requieren varias ejecuciones para garantizar estabilidad. En contraste, el modelo Kriging permite identificar óptimos locales con alta precisión. La metodología propuesta proporciona una estrategia eficiente para la toma de decisiones en ingeniería estructural, que promueve diseños de puentes más rentables sin comprometer el rendimiento estructural.
Figura. Paso superior en la autovía A-7, en Cocentaina (Alicante)
Los resultados indican que la optimización mediante modelos subrogados permite reducir significativamente los costes de diseño de pasos superiores pretensados. La estrategia adoptada optimiza variables como la profundidad de la losa, la geometría de la base y la resistencia del hormigón, y respeta las restricciones impuestas por los estados límite de servicio, que son los últimos según el Eurocódigo 2. Se observa que la metodología basada en kriging y la optimización heurística proporciona resultados prácticos con menor esfuerzo computacional en comparación con la optimización directa de todas las variables estructurales.
El modelo Kriging optimizado mediante Simulated Annealing identificó una configuración de losa con una profundidad de 1,30 m y una base de 3,15 m como la solución más rentable. Esta configuración se corrobora mediante la predicción de redes neuronales, lo que muestra coherencia en la localización del óptimo. En comparación con estudios previos, los resultados indican que la metodología utilizada en este trabajo permite obtener ahorros significativos sin necesidad de analizar exhaustivamente cada alternativa estructural.
A partir de los hallazgos obtenidos, se sugiere explorar la integración de métodos de optimización multiobjetivo que tengan en cuenta no solo el coste, sino también el impacto ambiental y los costes de mantenimiento a lo largo del ciclo de vida del puente. La inclusión de criterios de sostenibilidad podría mejorar la eficiencia global del diseño estructural y su capacidad de adaptación a normativas futuras.
Otra línea de investigación relevante consiste en aplicar modelos subrogados en el diseño de otros tipos de estructuras, como puentes de vigas o marcos de hormigón armado, para evaluar su viabilidad en distintas configuraciones estructurales. Además, el desarrollo de modelos predictivos más sofisticados, que integren aprendizaje automático y simulaciones de alta fidelidad, podría optimizar aún más los diseños propuestos.
Por último, se recomienda estudiar el impacto de la variabilidad de los materiales y las condiciones de carga en la optimización del diseño. La incorporación de análisis probabilísticos mejoraría la fiabilidad de las soluciones obtenidas, ya que se obtendrían diseños estructurales más robustos y seguros.
De izquierda a derecha: Ignacio Navarro, Rasmus Rampling, Mehrdad Hadizadeh, Salvador Ivorra, Tatiana García y Víctor Yepes
Hoy, 12 de febrero de 2025, ha tenido lugar la defensa de la tesis doctoral de D. Mehrdad Hadizadeh Bazaz, titulada “Inclusion of damage detection methods for the sustainable life cycle design of bridges in aggressive environments”, dirigida por los profesores Víctor Yepes Piqueras e Ignacio J. Navarro Martínez. La tesis recibió la calificación de sobresaliente «cum laude». A continuación, presentamos un pequeño resumen de la misma.
Resumen:
Para prevenir colapsos inesperados que pueden generar pérdidas económicas y humanas significativas, es esencial controlar la salud de cada estructura e infraestructura a lo largo de su ciclo de vida, que abarca desde su construcción y mantenimiento hasta su eventual retiro.
Sin embargo, las actividades de construcción, reparación y mantenimiento también pueden afectar al medio ambiente y a la sociedad. Por ello, el uso de técnicas modernas de detección de daños, que integren la evaluación sostenible del ciclo de vida y el análisis de los costes totales de mantenimiento, resulta fundamental para realizar reparaciones oportunas y minimizar el impacto negativo.
El concepto de sostenibilidad ha evolucionado desde su definición por primera vez por la Comisión Brundtland en 1987. Desde entonces, la comunidad científica ha desarrollado principios, métodos y criterios para el diseño sostenible, pero muchos de estos enfoques no son viables a largo plazo. En respuesta, las Naciones Unidas han establecido los Objetivos de Desarrollo Sostenible (ODS) para 2030.
En este contexto, es crucial adoptar una estrategia de ciclo de vida sostenible para las estructuras de hormigón que optimice costes y minimice el impacto ambiental y social en todas sus etapas, desde la construcción hasta el final de su vida útil. Los avances en tecnología informática y el desarrollo de sensores sofisticados han permitido implantar métodos de prueba no destructiva (NDT) para controlar y mantener de manera eficiente infraestructuras críticas, como puentes, y reducir así el riesgo de pérdidas económicas y humanas.
Esta tesis analiza la aplicación de diversas técnicas no destructivas para identificar daños estructurales y evalúa su impacto en la sostenibilidad. En este trabajo de investigación se evaluó el rendimiento de métodos no destructivos, como la función de respuesta en frecuencia (FRF) y la densidad espectral de potencia (PSD), para la detección y localización de daños estructurales. En particular, se analizó la capacidad de la PSD para predecir distintos tipos de daños en estructuras expuestas a la corrosión por iones de cloruro, como puentes de hormigón ubicados en entornos agresivos.
Posteriormente, se examinó la eficacia de este método de predicción en la evaluación del ciclo de vida sostenible, teniendo en cuenta su impacto ambiental, social y económico. Además, se analizaron los costes asociados a su aplicación en distintas fases de la vida útil de un puente de hormigón tipo cajón en Arosa, al noroeste de España.
Los resultados de esta tesis demuestran que la integración del método PSD en el mantenimiento preventivo durante el ciclo de vida de puentes de hormigón mejora significativamente su sostenibilidad. Los hallazgos confirman que la PSD permite detectar, localizar y predecir daños de manera eficiente, lo que optimiza la gestión a largo plazo de infraestructuras propensas a la corrosión. El análisis integral, que incorpora la evaluación del ciclo de vida y la toma de decisiones multicriterio, demuestra que la aplicación de la PSD reduce el impacto ambiental, minimiza los costes y mejora la sostenibilidad global de los puentes de hormigón. Además, este enfoque proporciona un marco adaptable a diversas infraestructuras y facilita el cumplimiento de objetivos de sostenibilidad a gran escala.
El puente Pumarejo, inaugurado en 1974 y fuera de servicio en 2019, cruza el río Magdalena, a 20 km de su desembocadura en el mar Caribe, entre Barranquilla y Sitionuevo, Magdalena. Conecta Barranquilla con la isla de Salamanca y la ruta hacia Ciénaga. Aunque oficialmente recibió el nombre de «Laureano Gómez», siempre fue conocido como el puente de Alberto Pumarejo, su principal impulsor.
De Jdvillalobos – File:Puente Pumarejo 001.JPG, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=27668196
Inicialmente, se pensó en ubicar el puente frente a la Zona Franca de Barranquilla, con una altura de 40 m, pero este diseño aumentaba el coste en 40 millones de pesos. Por ello, la administración de Lleras Restrepo (1966-1970) optó por un puente con un gálibo de 15 m. El proyecto fue obra del ingeniero Riccardo Morandi. La construcción empleó técnicas avanzadas de la época, como losas prefabricadas, pilotes de hasta 30 m de profundidad y grandes vigas pretensadas de hasta 120 t.
Este puente fue el más largo de Colombia hasta la inauguración del puente Roncador en 2020. Mide 1489 m de largo, divididos en tres secciones: 319 m en el acceso a Barranquilla, 282 m en el tramo atirantado y 887 m hacia Palermo. Con las vías de acceso, la longitud total fue de 3383 m. Los pilotes de hormigón armado tienen una profundidad de 30 m y un diámetro promedio de 1,80 m. El puente se apoya en 56 columnas y 29 tramos de vigas prefabricadas, con luces de hasta 140 m. Las pilas varían entre 2,5 y 5 m de diámetro y el ancho de la calzada es de 12,5 m, con una altura máxima de 16 m sobre el canal de navegación.
El ingeniero civil italiano Riccardo Morandi diseñó varias estructuras icónicas, como los puentes Américo Vespucio en Florencia (1957), General Rafael Urdaneta en Maracaibo (1962) y Wadi el Kif en Libia (1971). Lamentablemente, el 14 de agosto se derrumbó el puente Morandi en Génova, también diseñado por él, y dejó 39 muertos y al menos 11 edificios evacuados.
Puente de Akashi Kaikyo (Japón), 1998.
El Gran Puente del Estrecho de Akashi Kaikyō conecta Kōbe con la isla de Awaji y cruza uno de los estrechos más transitados del mundo, con más de 1000 embarcaciones al día. También conocido como Pearl Bridge, tiene una longitud total de 3911 m y está compuesto por tres vanos, siendo el central de 1991 m. Inaugurado el 5 de abril de 1998, se convirtió en el puente más largo del mundo de su tipo, superando al puente Humber del Reino Unido, con un tramo central de 1410 m. Fue diseñado por el ingeniero Satoshi Kashima y construido por Matsuo Bridge Co. El puente está sostenido por dos cables, considerados los más resistentes y pesados del mundo.
De Tysto – Self-published work by Tysto, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=477955
Durante la instalación de las torres y cables principales, ocurrió el Gran Terremoto de Hanshin (1995), que separó las torres casi un metro. Los cables del puente están hechos de 37,000 alambres de acero ultrarresistente, cuya longitud total daría siete vueltas y media a la Tierra si se colocaran en línea recta.
Se encuentra en una zona donde los tifones pueden alcanzar velocidades de hasta 290 km/h. Además, está ubicado en una región con gran actividad sísmica y, bajo su estructura, transitan diariamente cientos de embarcaciones.
Para la cimentación de las torres, se emplearon dos cajones circulares prefabricados de acero de 70 m de altura. El mayor tiene un diámetro de 80 m y el otro 78 m. Se utilizó el método de cajón descendente debido a la gran profundidad y las corrientes marinas. Se rellenaron con hormigón especial para endurecer con agua de mar. Cada anclaje requiere aproximadamente 350.000 toneladas de hormigón.
Los cimientos profundos de los anclajes se construyeron sobre tierras recuperadas mediante nuevas tecnologías. Estaban diseñados para resistir fuertes terremotos y se utilizó un método sísmico innovador y un hormigón especial, una mezcla de cementos resistentes al agua y la erosión. La capacidad de estos cimientos permitió que resistieran el fuerte terremoto del 17 de enero de 1995, con solo un desplazamiento de 1 m en las torres, lo cual es mínimo si se considera la magnitud del movimiento.
Viaducto de Millau (Francia), 2004.
El viaducto de Millau es un puente que cruza el valle del Tarn, en Aveyron (Francia), y soporta un tramo de la autopista A75, que conecta las causses Rouge y du Larzac. El viaducto es una estructura metálica atirantada de 2460 m de longitud, ligeramente curva, con un radio de 2000 m y una pendiente del 3,025 %. Está compuesto por ocho vanos atirantados: dos laterales de 204 m y seis centrales de 342 m, por lo que el viento puede superar los 200 km/h.
De Stefan Krause, Germany – Fotografía propia, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=8990774
Esta importante conexión nacional e internacional conecta Clermont-Ferrand con Béziers. Su construcción requirió trece años de estudios técnicos y financieros, iniciados en 1987, y se inauguró el 16 de diciembre de 2004, tres años después de colocar la primera piedra. Con un coste de 320 millones de euros, fue financiado por Eiffage mediante una concesión de 78 años, incluidos tres de construcción. A finales de la década de 2010, el viaducto registraba más de 4,5 millones de vehículos al año.
El viaducto de Millau fue diseñado por el ingeniero francés Michel Virlogeux, con la asesoría estética del arquitecto británico Norman Foster. Al proyectarse respetando la orografía, el viaducto necesitó siete grandes pilas huecas de hormigón de entre 50 y 60 cm de espesor. Sus alturas varían entre 78 y 245 m y están separadas entre sí por una distancia de 342 m. El hormigón B60, innovador en ese momento y con criterios de calidad excepcionales, fue el material principal utilizado para construir este viaducto.
Esta estructura cuenta con algunas de las pilas más altas del mundo. Bajo cada una de ellas hay pozos de cimentación con diámetros de entre 4 y 5 m y profundidades de entre 9 y 18 m, cubiertos por una losa de reparto de entre 3 y 5 m de espesor. El hormigonado de los encepados (hasta 2100 m³) se realizó en una sola fase con bomba.
Durante los días 3 y 4 de julio de 2024 tiene lugar en Jaén (España) el 28th International Congress on Project Management and EngineeringAEIPRO 2024. Es una buena oportunidad para debatir y conocer propuestas sobre dirección e ingeniería de proyectos. Nuestro grupo de investigación, en el marco del proyecto HYDELIFE, presenta varias comunicaciones. A continuación os paso los resúmenes.
SÁNCHEZ-GARRIDO, A.; GUAYGUA, B.; VILLALBA, P.; YEPES, V. (2024). Ingeniería de proyectos basada en modelos de análisis multivariante. Aplicación al dimensionamiento de losas planas aligeradas.28th International Congress on Project Management and Engineering, AEIPRO, 3-4 de julio, Jaén (Spain)
Esta investigación propone una metodología para dimensionar losas innovadoras de hormigón armado sin vigas que permiten un uso eficiente de los materiales. Utilizando un enfoque estadístico y modelos de regresión lineal, se proporcionan criterios para calcular el espesor de la losa aligerada con esferas o discos plásticos presurizados, minimizando el número de variables. Este espesor puede estimarse a partir de la luz principal entre apoyos, de la altura del disco o del diámetro de la esfera, así como del uso previsto del edificio. El modelo final ajustado logra explicar el 98% de la variabilidad del espesor de la losa para luces comprendidas entre 5 m y 16 m. Este tipo de forjado contribuye a la reducción del consumo de hormigón y acero, lo que resulta en una disminución del peso y de las cargas aplicadas. Esto impacta directamente en los costos y mejora los indicadores ambientales frente a los sistemas tradicionales. Se presenta como una alternativa eficiente para edificaciones, permitiendo combinar parámetros estructurales, constructivos y sostenibles.
SÁNCHEZ-GARRIDO, A.; YEPES-BELLVER, L.; SAIZ, D.; YEPES, V. (2024). Ingeniería de proyectos en Modernos Métodos de Construcción: El caso de edificios con losas planas mediante elementos aligerantes multiaxiales.28th International Congress on Project Management and Engineering, AEIPRO, 3-4 de julio, Jaén (Spain)
Los métodos modernos de construcción (Modern Methods of Construction, MMC), o como algunos la llaman “construcción inteligente”, constituyen alternativas a la construcción tradicional. Esta nueva forma de construir implica necesariamente un cambio en la forma de dirigir los proyectos, que pasan a ser industrializados, en los que la eficiencia estructural y constructiva, así como la sostenibilidad ambiental y social, son protagonistas. El objetivo del artículo es identificar los aspectos característicos de estas construcciones innovadoras que influyen en la ingeniería de proyectos, integrando a grupos multidisciplinares como arquitectos, ingenieros estructurales y empresas constructoras. Para ello, se realizará un estudio sobre el caso de edificios construidos con losas planas aligeradas mediante elementos aligerantes multiaxiales. Los resultados muestran que estos diseños permiten integrar el proyecto, la fabricación de elementos y el procedimiento constructivo. El proyecto de estas construcciones permite aligerar y reducir las cantidades de hormigón y acero en las zonas de las losas donde la capacidad portante es insignificante. Además, se ha comparado este diseño con otros tradicionales, destacando una reducción de costes y un aumento de la sostenibilidad a lo largo del ciclo de vida.
YEPES-BELLVER, L.; MARTÍNEZ-PAGÁN, P.; ALCALÁ, J.; YEPES, V. (2024). Análisis del predimensionamiento de tableros óptimos de puentes losa pretensados aligerados y su incidencia en el proyecto estructural.28th International Congress on Project Management and Engineering, AEIPRO, 3-4 de julio, Jaén (Spain)
El proyecto estructural suele basarse en la experiencia del proyectista. En ocasiones, dicha experiencia se plasma en fórmulas de predimensionamiento que, si bien ofrecen buenos resultados, en ocasiones arrastran ineficiencias cuando se comparan con técnicas actuales de optimización que tengan en cuenta las dimensiones económicas y ambientales. En este artículo se comparan reglas de dimensionamiento previo de estructuras basadas en la experiencia con técnicas de optimización. Se aplica al caso del proyecto de tableros de puentes tipo losa pretensados aligerados. El resultado de la investigación resalta la importancia de aplicar métodos basados en la optimización heurística y en metamodelos para actualizar la experiencia de los proyectistas y proponer nuevas fórmulas de predimensionamiento más ajustadas a la optimización económica y ambiental. Además, en el trabajo se ofrecen nomogramas de predimensionamiento, con el mínimo número de datos posible, que pueden ser de utilidad al proyectista en sus diseños previos.
Quisiera felicitar públicamente a nuestro estudiante de doctorado Mehrdad Hadizadeb-Bazaz por su Premio al mejor trabajo en la modalidad de póster otorgado por la Escuela de Doctorado de la Universitat Politècnica de València, dentro del IX Encuentro de Estudiantes de Doctorado. Tengo el honor y el placer de dirigir su tesis doctoral junto con el profesor Ignacio J. Navarro. El trabajo se enmarca dentro del proyecto de investigación HYDELIFE que dirijo como investigador principal. Es el segundo año consecutivo que Mehrdad consigue este premio.
Hoy en día, debido a los elevados costes de construcción, reparación y mantenimiento de grandes estructuras como los puentes, así como la creciente atención al ciclo de vida sostenible en todas las etapas, desde el diseño hasta el final de su vida útil, es crucial emplear diversos métodos para identificar daños y evaluar su eficacia en diferentes estructuras y condiciones. Esto no solo puede aumentar la vida útil de las estructuras y reducir los costes, sino también minimizar el impacto ambiental y social.
En este estudio, se examina la precisión de diversos métodos de detección de daños, tanto dinámicos como no destructivos, para identificar la magnitud, ubicación y momento en que se produce el daño en la estructura a lo largo de su vida útil. Se evalúa la precisión y posibles variaciones de cada uno de los métodos de detección de daños en distintos entornos, especialmente en ambientes costeros y ambientes agresivos. Además, se realiza una evaluación del desempeño y comparación de diferentes métodos de detección de daños no destructivos, teniendo en cuenta casos de sostenibilidad de diseño y evaluación del ciclo de vida, incluyendo aspectos económicos, ambientales e impactos sociales.
Os dejo el póster completo, para que lo podáis leer.
Figura 2. Encofrado perdido de hormigón entre vigas prefabricadas de puente.
El empleo del hormigón como encofrado se utiliza en distintos casos de forma eficiente. En el caso de puentes de vigas, se utiliza en prelosas o losas, ya sean armadas o pretensadas, integrándose a la sección resistente de la pieza de hormigón mediante una conexión adecuada. Estos elementos sirven, cuando se hormigona, como encofrados perdidos de hormigón entre las vigas prefabricadas de un puente (Figura 1). Los encofrados perdidos pueden ser de distintos materiales, pero este artículo se centra en los fabricados en hormigón.
La placa de encofrado perdido es un componente construido con hormigón pretensado esencial para la conformación de los tableros de vigas. Por un lado, actúan como elementos autoportantes que sirven como encofrado del tablero durante la fase de hormigonado “in situ”, eliminando la necesidad de emplear otros sistemas de encofrado de la estructura. Por otro lado, colaboran en las cargas del puente en servicio. Normalmente, son de sección maciza, aunque también se han llegado a fabricar losas alveoladas.
Estos elementos se ubican entre las alas superiores de las vigas, proporcionando un soporte para la instalación de la armadura de la losa in situ, lo que facilita el vertido de hormigón y actúa como encofrado. De este modo, el elemento queda completamente integrado dentro del hormigón de la losa. Estas prelosas están compuestas por una losa de hormigón con un espesor variable entre 6 y 20 cm, junto con celosías o nervios de acero dispuestos a lo largo de toda su longitud, ya sea de sección constante o variable.
Se pueden dar varios tipos:
Losas de encofrado perdido entre vigas
Esta técnica es comúnmente utilizada para encofrar los espacios entre vigas doble T o vigas artesa, así como los vanos internos en las vigas artesa (Figura 1). Sin embargo, no permiten la creación de voladizos en el exterior de las vigas laterales. Normalmente, tienen un espesor de 6 a 7 cm, aunque en casos excepcionales puede reducirse a 5 cm, o bien emplear otros materiales, como chapas grecadas, que son comunes en tableros de vigas adosadas en T invertida.
Prelosas o semilosas entre vigas o con vuelos exteriores
Presentan espesores de hasta 8 cm, tal y como se muestra en la Figura 2. Sin embargo, valores más altos no resultan económicos y generan acciones en las vigas difíciles de compensar, especialmente al actuar sobre la sección de la viga sola. Además, dificultan la colocación de armaduras in situ, especialmente para el anclaje de los pretiles de borde. Para contrarrestar estas dificultades, se emplean disposiciones de armadura en forma de celosía plana (una barra superior y una inferior) o de sección triangular (una barra superior y dos inferiores), hormigonando luego el espesor restante de la losa. En caso necesario, se incorporan conectores de armadura entre ambos hormigones. Este sistema se ha utilizado en tableros con grandes vuelos exteriores y amplias separaciones entre vigas para las losas de tablero pretensadas transversalmente, aunque no es una solución común. Algunos fabricantes ofrecen una variante compleja de prelosas con formas especiales, como nervios rigidizadores o quebradas, que pueden alcanzar anchuras del orden de 15 m. Esta solución es frecuente en estructuras mixtas, con vigas metálicas (Figura 3), o en ampliaciones de puentes existentes, donde en lugar de una viga artesa prefabricada se utiliza un zuncho de apoyo y anclaje en la estructura existente.
Figura 2. Losas de hormigón pretensado como encofrado colaborante entre vigas de puente. http://www.paolini.com.ar/montaje-vigas-preslosas-del-puente/
Figura 3. Losas de hormigón pretensado como encofrado colaborante entre vigas de puente mixto. http://www.paolini.com.ar/montaje-vigas-preslosas-del-puente/
Losas de espesor completo
Son frecuentes en proyectos de ampliación de trazados, como carreteras a media ladera y estructuras existentes, donde los equipos de construcción pueden circular sobre las losas ya instaladas, agilizando considerablemente el progreso de la obra (Figura 4). Por lo general, estas losas cubren toda la anchura del tablero y se utilizan en tableros que descansan sobre dos vigas en doble T o una monoviga. Se unen entre sí mediante juntas transversales in situ y a las vigas mediante ventanas también hormigonadas in situ, lo que permite que los conectores de las vigas se coloquen en áreas localizadas en lugar de distribuirse por toda la viga sin interrupciones. En el caso de que no cubran toda la anchura del tablero, requieren juntas longitudinales, las cuales son más complicadas de realizar, ya que afectan la armadura transversal del tablero, que es más importante y densa que la armadura longitudinal.
Figura 4. Losa de espesor completo. Fuente: https://www.prenava.com/prelosas-semilosas-losas-vigas-y-jabalcones-prefabricados-para-tableros-de-puente/
A continuación os dejo un vídeo de montaje de prelosas y vigas.
Referencias:
AFECI (2021). Guía sobre encofrados y cimbras. 3ª edición, Asociación de fabricantes de encofrados y cimbras, 76 pp.
Los días 10 a 12 de junio de 2025 se celebró en Edimburgo (Reino Unido) uno de los congresos más importantes sobre optimización de estructuras: “12th International Conference on High Performance and Optimum Design of Structures and Materials, HPSM/OPTI 2025“. He participado en dicho congreso tanto en su Comité Científico como Invited Speaker.
Metodología empleada
