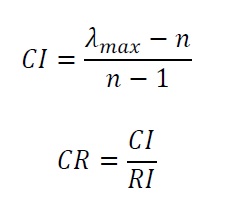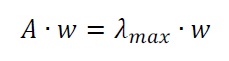El dilema del guepardo y el halcón
El dilema del guepardo y el halcón
En nuestra búsqueda de la excelencia, tendemos a caer en la especialización extrema. Admiramos al guepardo, cuya fisonomía está diseñada para ser el proyectil terrestre definitivo; nos asombra el halcón peregrino, capaz de desafiar la gravedad y alcanzar velocidades de vértigo; y respetamos al pez espada, que se desplaza por el océano con una hidrodinámica inigualable. Cada uno es el «mejor» en su ámbito. Sin embargo, en el tablero de la supervivencia y la estrategia, la excelencia en un solo campo no garantiza el éxito global.
El problema radica en que la realidad rara vez es unidimensional. El dilema del guepardo y el halcón nos muestra que ser el número uno en una categoría puede dejarnos vulnerables cuando el entorno nos exige operar en medios distintos. La «mejor» decisión no surge de la búsqueda ciega de la perfección en un solo criterio, sino de un ejercicio sofisticado de equilibrio.
La paradoja del pato: la versatilidad frente a la especialización.
Desde la perspectiva de la ciencia de las decisiones, el pato es el ganador inesperado de esta contienda evolutiva. Aunque no corre tan rápido como un guepardo, no vuela con la potencia de un halcón ni nada con la destreza de un pez espada, el pato puede realizar las tres acciones con eficacia. En un modelo de decisión multicriterio, el pato representa una «solución de compromiso»: aquella que maximiza la utilidad global en diversos escenarios.
Técnicamente, decidir no es simplemente elegir. Es un proceso de optimización que requiere rigor conceptual.
«Decisión: elegir la mejor opción posible. Hay que definir qué significa mejor y qué significa posible».
El pato triunfa porque cumple con lo «posible» (su conjunto de alternativas factibles es más amplio) y redefine lo «mejor» desde un enfoque sistémico. Mientras que el guepardo es una solución óptima para un conjunto finito de restricciones terrestres, el pato es la respuesta robusta ante un mundo de variables múltiples.
Comparar manzanas con naranjas: el arte de la normalización.
El mayor obstáculo estratégico al evaluar opciones es la disparidad de unidades. ¿Cómo se sopesa el beneficio de la velocidad frente al coste del riesgo o el precio de un activo? Aquí es donde entra en juego la normalización, una técnica matemática que permite unificar escalas y convertir los datos xij en valores adimensionales mij comparables entre sí.
Para un estratega, la normalización no es solo un ajuste de escala, sino un cambio de lógica. Debemos distinguir entre los criterios de beneficio (donde más es mejor) y los de coste (donde menos es mejor).
Sin normalización vectorial o lineal, nuestras decisiones diarias fallan, ya que nuestras escalas mentales están descalibradas y otorgamos un peso desproporcionado a lo que es fácil de medir, ignorando lo que realmente importa.
Lógica difusa: traduciendo la ambigüedad en números reales.
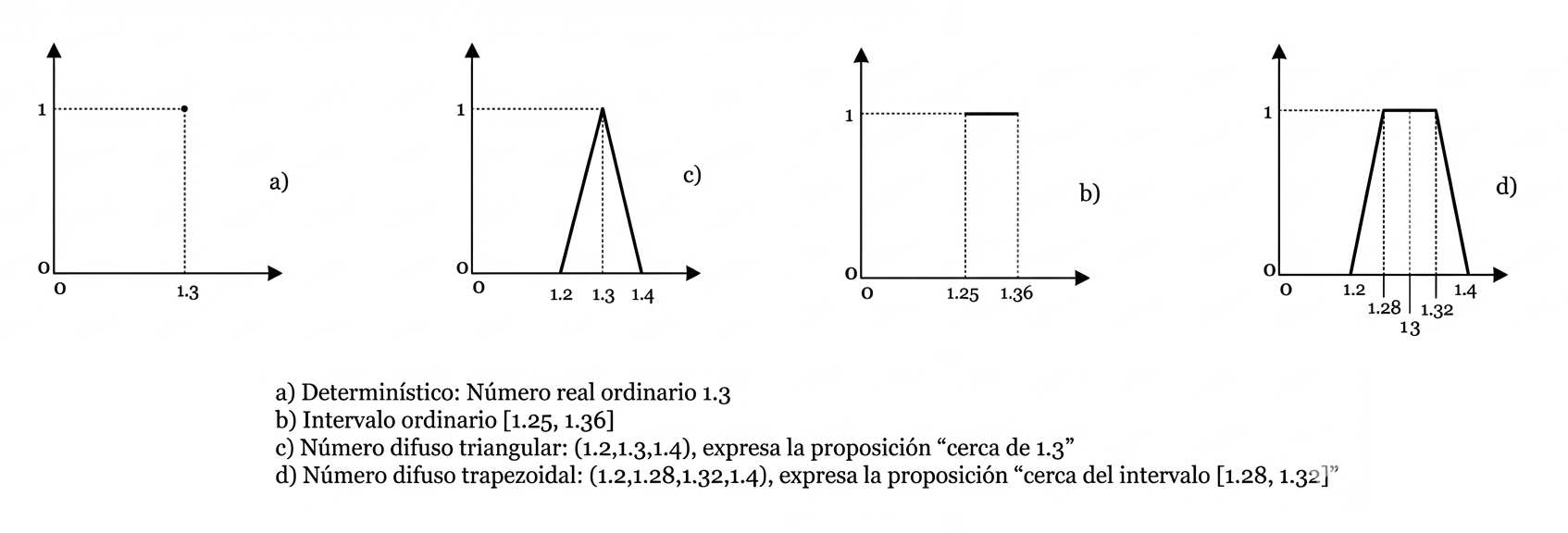
En la estrategia real, los datos rara vez son determinísticos. El lenguaje humano es vago: decimos que una oportunidad es «muy buena» o «normal». La ciencia de la decisión estructura esta incertidumbre mediante la lógica difusa, que transforma los juicios lingüísticos en números triangulares difusos (NTD).
Un NTD se define por tres valores (L, M, U):
- L (más bajo): el límite inferior o el escenario más pesimista.
- M (moda): el valor más probable o el núcleo del juicio.
- U (más alto): el límite superior o el escenario más optimista.
Por ejemplo, la expresión «muy bueno» podría representarse como (0,6; 0,7; 0,8). Esta tríada no es arbitraria, sino que representa el «margen de error» y la vaguedad intrínseca de la percepción humana. Al utilizar estos intervalos, pasamos de una falsa precisión a una objetividad robusta que acepta y cuantifica la duda.
El axioma de Zeleny: la búsqueda del «punto ideal».
¿Cómo identificar la mejor opción en un mar de alternativas? El axioma de Zeleny postula que la solución preferida es la que minimiza la distancia al «punto ideal». Imaginemos un animal hipotético que corriera como el guepardo, volara como el halcón y nadara como el pez espada: ese sería nuestro punto ideal, una utopía técnica.
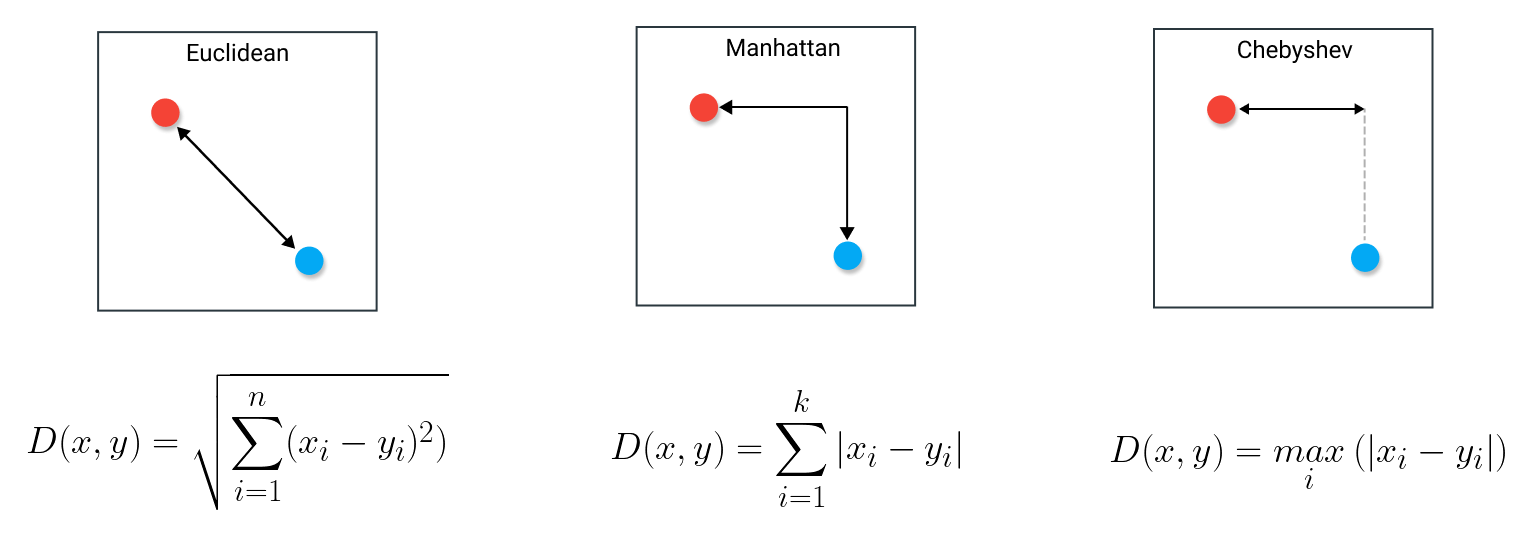
Para medir cuán cerca estamos de ese ideal, utilizamos funciones de distancia Lp, cuya interpretación cambia nuestra postura estratégica.
- La distancia de Manhattan (L₁) es una métrica compensatoria. Suma todas las diferencias, lo que permite que una gran fortaleza en un área compense una debilidad en otra.
- La distancia euclidiana (L₂) es la distancia física más directa en un espacio multidimensional y es la medida estándar de proximidad.
- La distancia de Chebyshev (L∞) es la medida más conservadora. Se enfoca exclusivamente en la mayor diferencia posible, buscando minimizar el «máximo dolor». Es la estrategia de quien no puede permitirse un solo fallo crítico.
El pato no es perfecto, pero su distancia euclidiana al ideal es menor que la de los especialistas cuando el entorno exige versatilidad.
El filtro de la consistencia: no te contradigas.
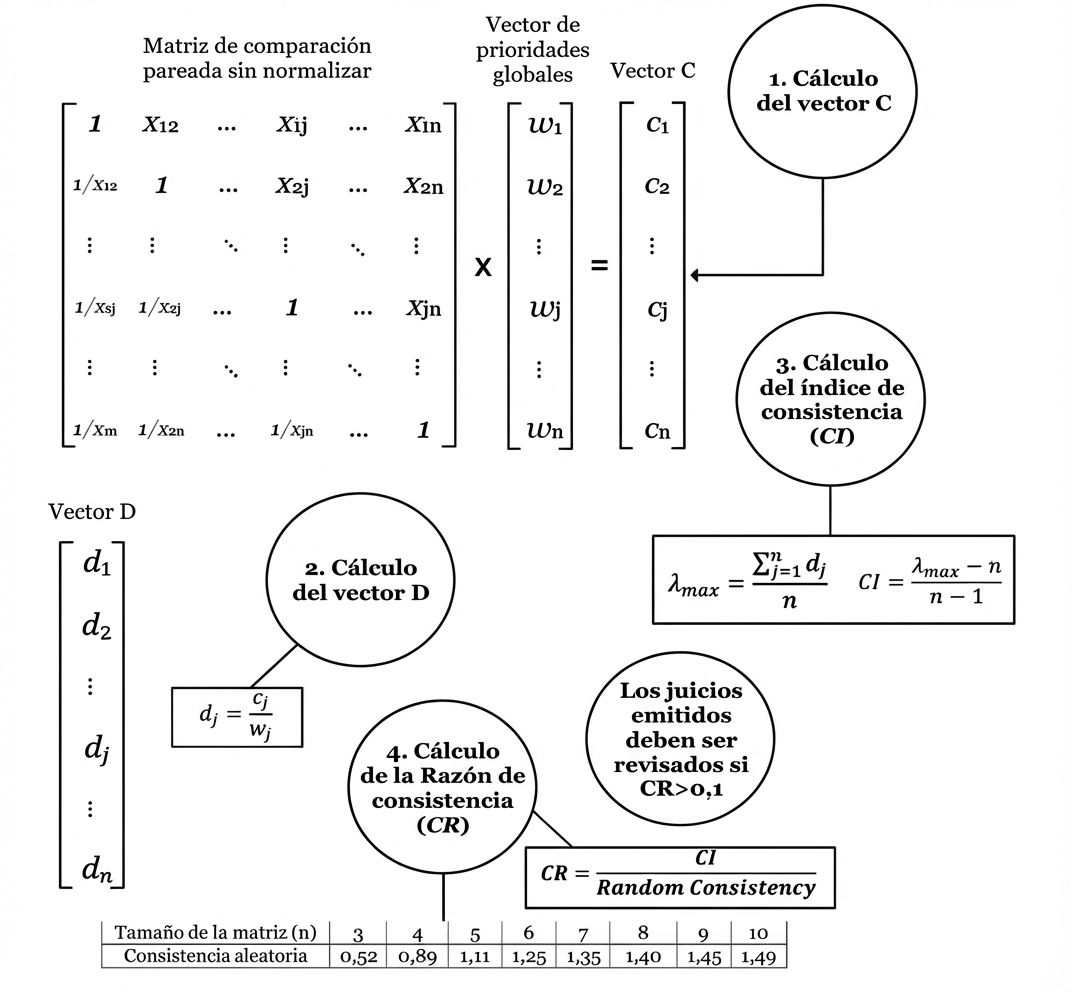
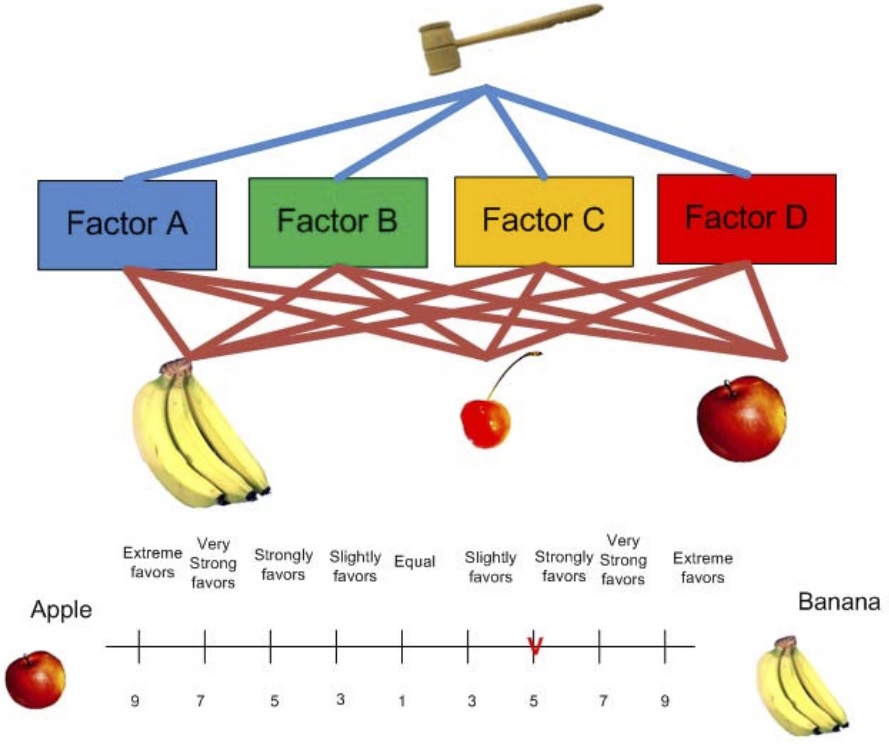
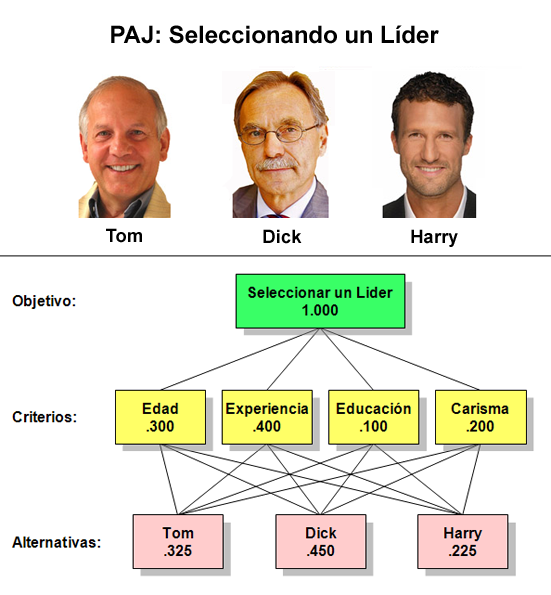
Incluso con las mejores herramientas, la calidad de una decisión depende de la lógica del decisor. El Proceso de Jerarquía Analítica (AHP) nos obliga a ser coherentes mediante matrices de comparación pareada que deben respetar tres propiedades fundamentales.
- Reciprocidad: si la opción A es tres veces mejor que la B, entonces la B debe ser, obligatoriamente, una tercera parte tan buena como la A.
- Homogeneidad: los elementos comparados deben pertenecer al mismo orden de magnitud para que la escala tenga sentido.
- Consistencia: si prefieres A sobre B y B sobre C, sería una contradicción lógica preferir C sobre A.
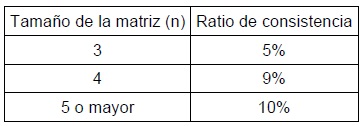
El AHP calcula una razón de consistencia (CR). Si este ratio es elevado, el «autovector» (o vector de prioridades) de la decisión se distorsiona y el juicio pierde validez.
«Los juicios emitidos deben ser revisados si la razón de consistencia es mayor que 0,1».
En la alta estrategia, el objetivo es minimizar este valor para garantizar que nuestras prioridades sean lógicamente sólidas y no fruto de un sesgo momentáneo.
Conclusión: Hacia una estrategia de vida «multicriterio».
La ciencia de la decisión nos enseña que el éxito no es una carrera de cien metros lisos, sino un triatlón constante. Para diseñar vidas y negocios más equilibrados, debemos evolucionar de la optimización simple a la estrategia multicriterio.
- Sintetizar la versatilidad: hay que dejar de buscar la especialización extrema y empezar a valorar las «soluciones de compromiso» que ofrecen solidez.
- Normalizar con rigor: antes de comparar, ajuste sus escalas. No ignore el coste por deslumbrarse con el beneficio.
- Gestionar la incertidumbre: utilice la lógica difusa para aceptar que sus juicios tienen márgenes de error (L, M, U).
- Medir la distancia al ideal: defina su punto ideal, pero tenga en cuenta si opera bajo una lógica de compensación (L₁) o de mitigación de riesgos (L∞).
- Exigirse consistencia: si sus prioridades se contradicen, su estrategia colapsará. Mantenga su CR < 0,1.
Al final del día, el pato sobrevive porque es consistente en su mediocridad brillante a través de múltiples medios. ¿Qué criterio fundamental está sacrificando hoy por obsesionarse con una sola métrica de éxito?
En esta conversación puedes escuchar las ideas más interesantes sobre la toma de decisiones.
Una buena síntesis de las ideas sobre este tema la puedes encontrar en el siguiente vídeo.
Aquí dejo un documento de síntesis que espero os resulte útil.
Optimizing_Multicriteria_Decisions

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.