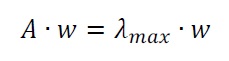 En varios artículos de este blog hemos descrito distintos aspectos del Proceso Analítico Jerárquico (Analytic Hierarchy Process, AHP). Se trata de una técnica de decisión Multicriterio propuesta por T.L. Saaty que combina aspectos tangibles e intangibles para obtener, en una escala de razón, las prioridades asociadas con las alternativas del problema. No obstante, AHP presenta limitaciones que debemos conocer antes de utilizar este método.
En varios artículos de este blog hemos descrito distintos aspectos del Proceso Analítico Jerárquico (Analytic Hierarchy Process, AHP). Se trata de una técnica de decisión Multicriterio propuesta por T.L. Saaty que combina aspectos tangibles e intangibles para obtener, en una escala de razón, las prioridades asociadas con las alternativas del problema. No obstante, AHP presenta limitaciones que debemos conocer antes de utilizar este método.
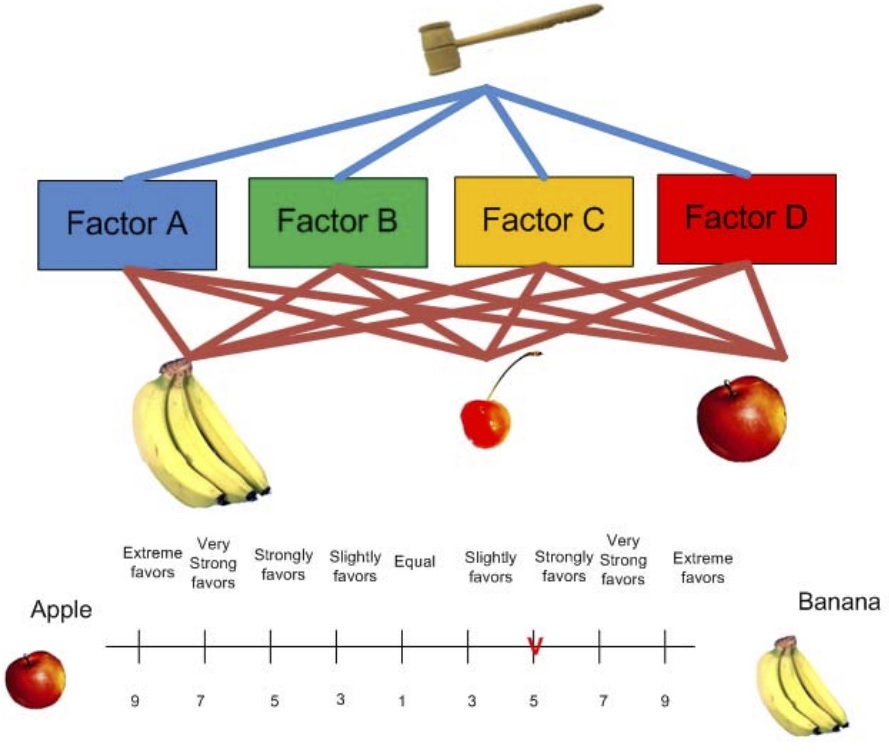
Pues bien, una de las ventajas de AHP es que permite medir la consistencia del decisor al emitir sus juicios. Este aspecto es muy relevante, puesto que si decimos que A>B y que B>C, no podemos decir que A<C. Este aspecto es de gran interés cuando consultamos a expertos en una materia para comprobar que la información que nos facilita es correcta. Si la consistencia es aceptable, se puede continuar con el proceso de decisión. Pero si no lo es, entonces el que toma las decisiones debe replantearse sus juicios sobre las comparaciones pareadas antes de continuar con el análisis.
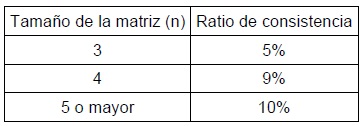
Saaty sugiere para el método AHP convencional (en el que se utiliza el método del autovector principal para obtener las prioridades), que la inconsistencia sea capturada mediante un único valor denominado índice de consistencia (Consistency Index, CI) donde λmax es el máximo autovalor y n es la dimensión de la matriz de decisión. Un índice de consistencia igual a cero significa que la consistencia es completa. Como esta medida depende del orden de la matriz (n), Saaty propone la utilización de la Razón de Consistencia (CR) que se obtiene dividiendo CI por su valor esperado RI, calculado a partir de un gran número de matrices recíprocas positivas de orden n generadas aleatoriamente (Tabla 1). Por tanto, una vez la matriz es consistente siempre y cuando CR no supere los valores indicados en la Tabla 2. Si en una matriz se supera el CR máximo, hay que revisar las ponderaciones.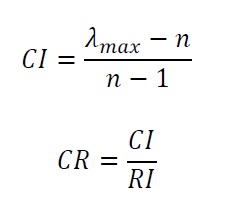
Donde RI es el índice aleatorio, que indica la consistencia de una matriz aleatoria (Tabla 1):

Una vez verificada la consistencia, se obtienen los pesos, que representan la importancia relativa de cada criterio o las prioridades de las diferentes alternativas respecto a un determinado criterio. Para ello, el AHP original utiliza el método del autovector principal por la derecha, basado en el teorema de Perron-Frobenius, donde hay que resolver la siguiente ecuación:
donde A representa la matriz de comparación, w el autovector o vector de preferencia, y λmax el autovalor.
En la práctica, el vector de los pesos w=(w1, w2,…, wn) se obtiene (método de las potencias) elevando la matriz de juicios a una potencia suficientemente grande, sumando por filas y normalizando estos valores mediante la división de la suma de cada fila por la suma total. El proceso concluye cuando la diferencia entre dos potencias consecutivas sea pequeña.
Sin embargo, este vector de los pesos de cada alternativa también se pueden calcular por el método de la media geométrica por filas (Crawford y Williams, 1985). En este caso, el peso de cada prioridad se calcula como la media geométrica por filas normalizado a la suma de las medias geométricas de todas las filas. Este método se está utilizando ampliamente en los últimos años por sus propiedades matemáticas y sociológicas. Los resultados de este método, comparados con el cálculo del autovector, son parecidos, aunque su cálculo es más sencillo.
De todas formas, os dejo un vídeo del profesor Aznar donde se explica con cierto detalle cómo calcular la consistencia y el autovector. Espero que os sea de utilidad.
Referencias:
AZNAR, J.; GUIJARRO, F. (2012). Nuevos métodos de valoración: modelos multicriterio. Editorial Universitat Politècnica de València.
CRAWFORD, G.; WILLIAMS, C. (1985). A note on the analysis of subjective judgement matrices. Journal of Mathematical Psychology, 29:387-405.
SAATY, T.L. (1980). The Analytic Hierarchy Process: Planning, Priority Setting, Resource Allocation, McGraw-Hill.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.