Polimedia – Página 2 – El blog de Víctor Yepes

Clasificación de las cimbras autolanzables

Figura 1. Clasificación de las autocimbras

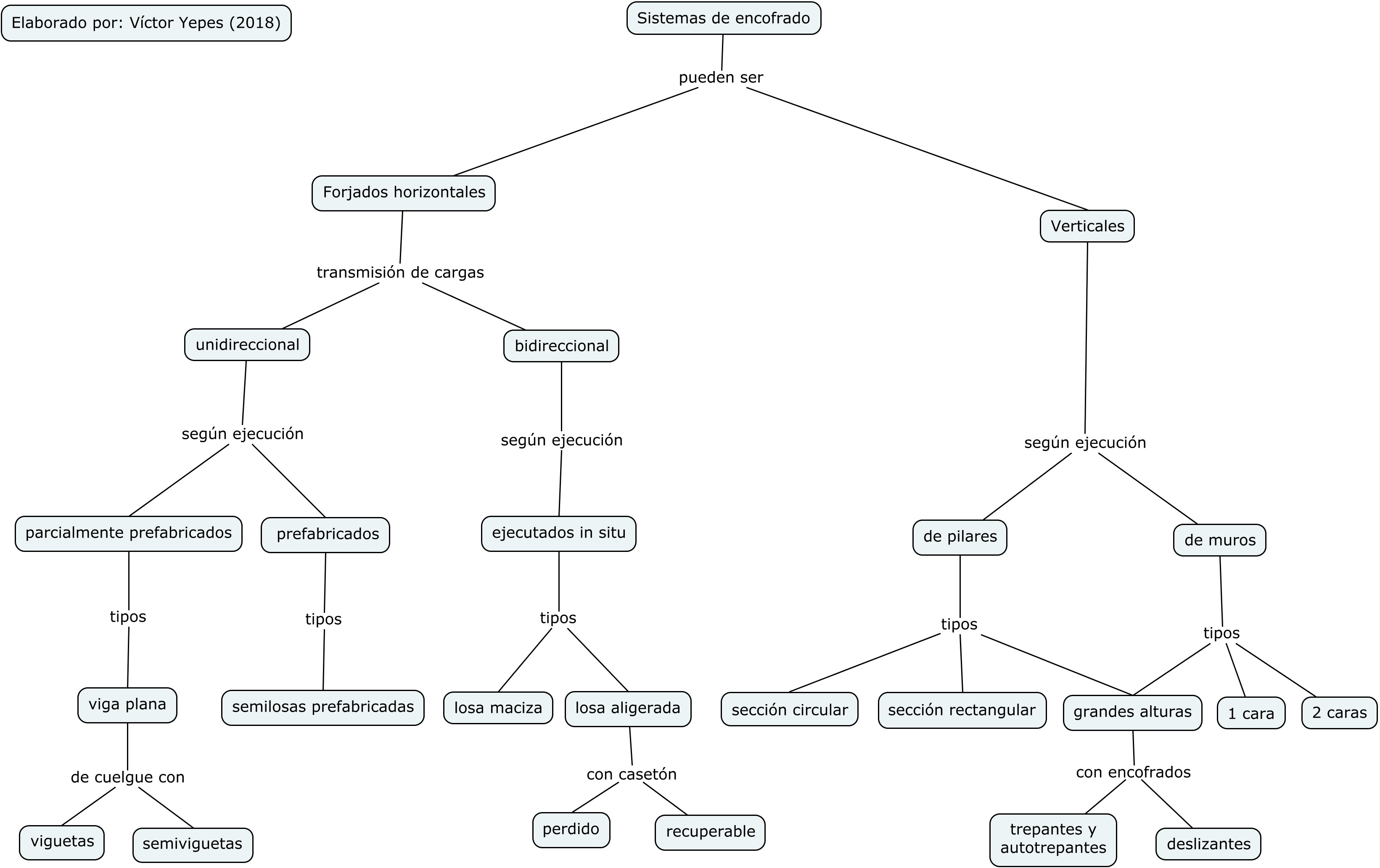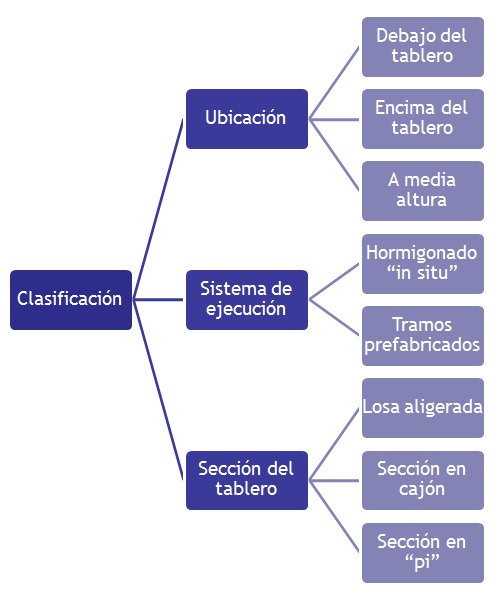
En una entrada anterior se definieron las cimbras autolanzables. Aquí vamos a clasificar las cimbras atendiendo a diversos criterios como son su ubicación, su sistema de ejecución y la sección del tablero (Figura 1). Se trata, por tanto, de diferenciar las distintas tipologías de autocimbras en función de esta clasificación.

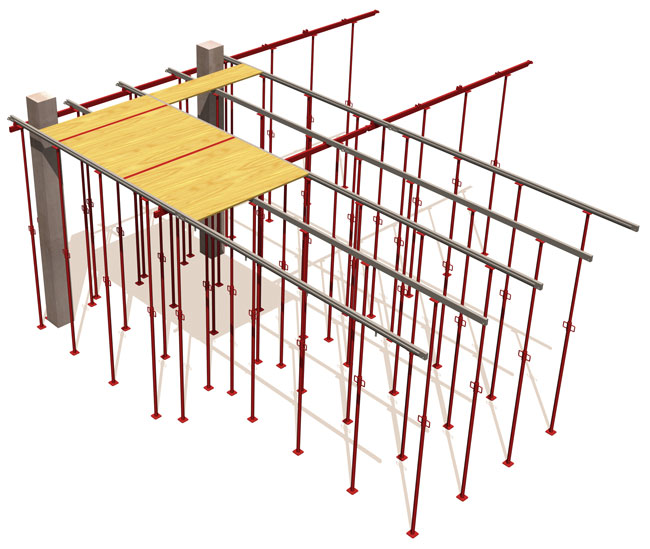
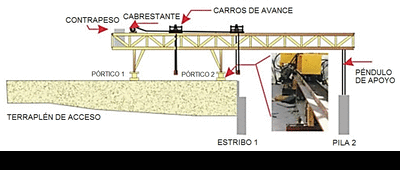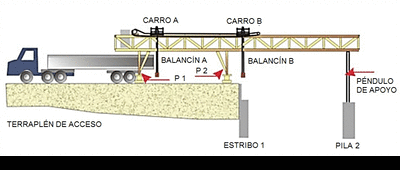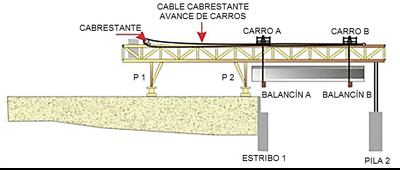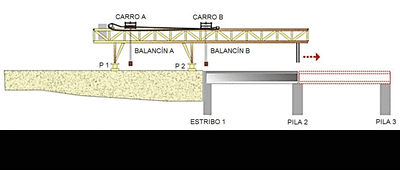
Si atendemos a la ubicación de la autocimbra, ésta se puede clasificar en cimbras autolanzables sobre tablero, bajo tablero o a media altura. En las autocimbras sobre tablero, las vigas longitudinales se colocan por encima del tablero y de ellas cuelgan elementos que soportan las vigas donde se apoya el encofrado (Figura 2). Las autocimbras bajo tablero son las más habituales; aquí las vigas longitudinales principales se sitúan debajo del tablero a construir (Figura 3). Una variante de la cimbra bajo tablero es la situada a media altura; en este caso, las vigas longitudinales se colocan debajo de las alas y próximas a ellas (Figura 4). En este caso el fondo del tablero se encuentra por debajo o a la misma altura de las vigas.

Figura 2. Cimbra autolanzable sobre tablero

Figura 3. Cimbra autolanzable bajo tablero

Figura 4. Cimbra autolanzable a media altura. www.mecanotubo.es

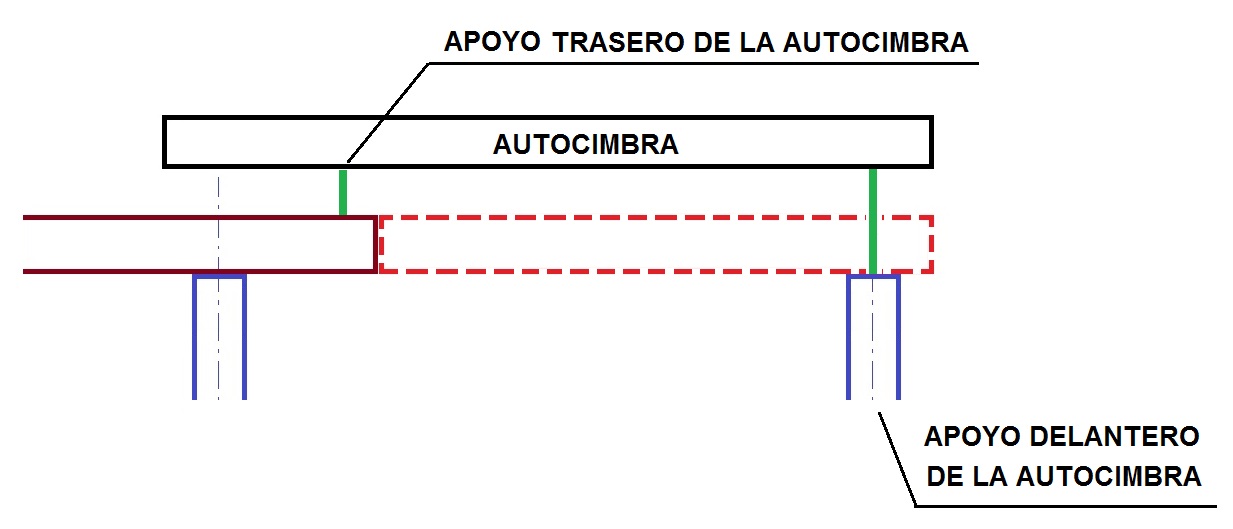
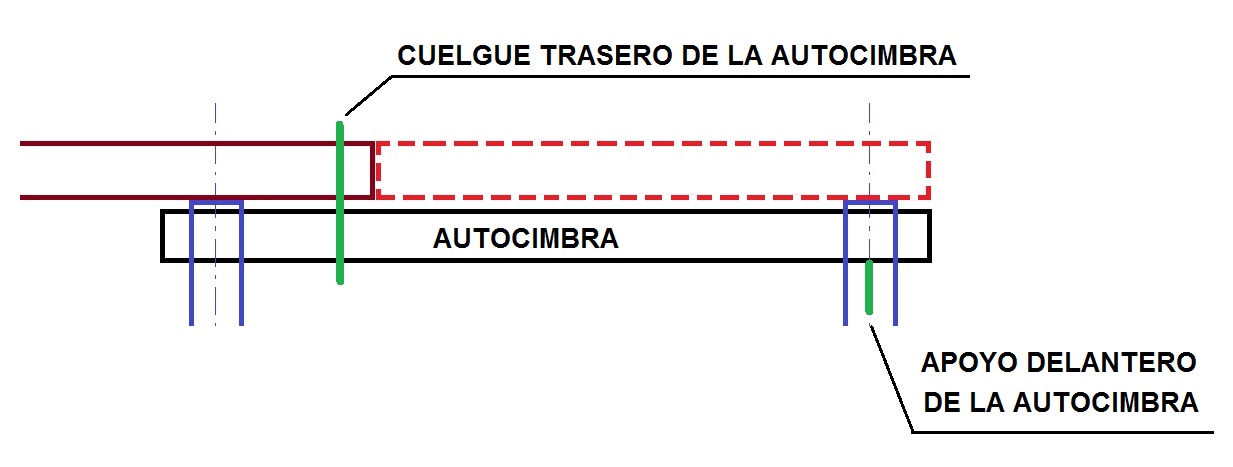
Atendiendo al sistema de ejecución, la cimbra autolanzable propiamente dicha sería la que sirve para hormigonar el tablero “in situ”; es decir, primero se coloca la ferralla y luego se hormigona sobre el encofrado. Sin embargo, también se podrían incluir en esta clasificación aquellas cimbras autolanzables que sirven para colocar tramos prefabricados, bien dovelas o vanos completos. En este caso estaríamos hablando más de un lanzador de vigas o de dovelas que una autocimbra propiamente dicha.

Por último, si atendemos a la sección del tablero, las autocimbras sirven para construir tableros de losa aligerada, cuando las luces de vano están comprendidas entre los 30 y 40 m. El aligeramiento suele ser de poliestireno expandido. Otra opción son las secciones tipo Pi o multinervadas; en este caso no existe encofrado interior, la sección resulta muy ligera, se usa para luces máximas de 35 m. Como inconveniente se puede decir que precisa de grandes cantos para soportar los momentos negativos. La sección en cajón es la opción empleada tanto en cimbras por encima como por debajo del tablero, en luces entre 40 y 80 m. En este caso el encofrado interior complica el desencofrado y el rendimiento.

A continuación os dejo un Polimedia donde se explica con mayor detalle estos aspectos de la clasificación de las autocimbras.

Referencias:

MARTÍ, J.V.; YEPES, V.; GONZÁLEZ, F. (2004). Temas de procedimientos de construcción. Cimbras, andamios y encofrados. Editorial de la Universidad Politécnica de Valencia. Ref. 2004.441.

SEOPAN (2015). Manual de cimbras autolanzables. Tornapunta Ediciones, Madrid, 359 pp.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Definición de cimbra autolanzable

Viaductos en la nueva autovía de Mascara (Argelia). Imagen: A. Azorín

Una cimbra autolanzable es aquel medio auxiliar empleado para el hormigonado de tableros de puentes o viaductos vano a vano de hormigón postesado. También reciben el nombre de autocimbra, cimbra de avance o cimbra MSS (Movable Scaffolding System, en inglés). Son estructuras auxiliares capaces de trasladarse a lo largo del puente por sus propios medios, por lo que se trata realmente de una cimbra-máquina, con los problemas asociados de cálculo por su movilidad. La cimbra de avance se caracteriza por su capacidad de trasladarse de una posición a la siguiente por sus propios medios, lo cual disminuye el uso de grúas. Ello le permite salvar obstáculos o alturas importantes, así como evitar las posibles obstrucciones en vías de tránsito.

En este post os defino brevemente esta cimbra, pero en sucesivos posts seguiré dando detalles y explicando con mayor profundidad los tipos existentes, elementos, parámetros, etc.

La autocimbra es una estructura en celosía o cajones metálicos longitudinales que soportan el encofrado. Esta estructura es capaz de alcanzar la distancia existente entre las pilas del puente. Si el vano es inferior a 40 m, suelen emplearse vigas de longitud el doble del tramo, no usándose cimbras tipo regla de cálculo. Durante el hormigonado, la estructura se apoya en la pila delantera y en el tramo del tablero ya construido.

El uso habitual de esta cimbra es en tableros de puentes de hormigón postesado, preferentemente con vanos de luces iguales y con canto constante. Su aplicabilidad se encuentra entre luces de 30 y 70 m, aunque la cimbra autolanzable más grande del mundo alcanza vanos de 90 m. Para que os hagáis una idea, la Dirección General de Ferrocarriles, del Ministerio de Fomento, recomienda, con carácter general, usar la autocimbra por encima de 40 m de luz. Sin embargo, también recomienda utilizar la autocimbra en la construcción de tableros hiperestáticos de hormigón que cumplan alguna de las siguientes condiciones: (a) número de vanos entre 3 y 5, (b) cuando la longitud total del puente sea menor a 300 m, pero con 6 vanos o más, (c) cuando la longitud total del puente supere los 300 m, con 6 vanos o más y la altura del tablero respecto al suelo sea de 15 m o menos. En las referencias he dejado dichas recomendaciones completas.

El M1-90-S es la más grande cimbra autolanzable del mundo (vanos de 90 m). http://www.berd.eu/es/produtos/movable-scaffolding-system/

Con carácter general, se puede decir que la autocimbra es rentable cuando el puente tiene más de 7-8 vanos, más de 500 m de luz y se usa al menos cuatro veces. Para secciones de losa aligerada, las luces habituales suelen estar entre 30 y 40 m, mientras que para sección en cajón, se encuentran entre 40 y 70 m. También son rentables en el caso de construir puentes con doble tablero y existe facilidad de trasladar la autocimbra de uno al otro. También es favorable el caso de tener que construir diferentes viaductos de la misma obra si el traslado es factible.

Por otra parte, el procedimiento constructivo suponen esfuerzos que deben considerarse en el cálculo de la estructura. Se coloca la junta de construcción entre fases a una distancia entre L/4 y L/5 de la pila para reducir los flectores sobre el tablero. Además, a unos 2 m de la junta es donde se apoya la autocimbra sobre el tablero hormigonado. Las esbelteces normales del tablero oscilan entre 1/18 y 1/20.

La autocimbra transmite esfuerzos a la fase anterior durante el hormigonado. Se trata de una acción transitoria, no siendo raro que supere las 1000 t durante el hormigonado. Esta acción es como si la ley de flectores de peso propio al construir con autocimbra se desplazara hacia arriba. Sin embargo, al final del proceso constructivo los esfuerzos debidos a peso propio y al pretensado se redistribuyen, de forma que la ley de flectores se aproximará a la que tendría si se hubiese cimbrado el puente de forma convencional. Todo ello significa que las situaciones pésimas de comprobación serán en la sección del tablero en pilas a corto plazo y en la sección de centro de vano a largo plazo.

Todo lo que os he descrito en el artículo os lo cuento en el siguiente Polimedia, que espero os guste. En otras entradas os contaré más detalles de las autocimbras como su clasificación, elementos o parámetros para seleccionarlas.

También os dejo una animación en la que se puede ver el funcionamiento de la autocimbra.

Referencias:

MARTÍ, J.V.; YEPES, V.; GONZÁLEZ, F. (2004). Temas de procedimientos de construcción. Cimbras, andamios y encofrados. Editorial de la Universidad Politécnica de Valencia. Ref. 2004.441.

SEOPAN (2015). Manual de cimbras autolanzables. Tornapunta Ediciones, Madrid, 359 pp.

MINISTERIO DE FOMENTO (2009). Recomendaciones de la Subdirección General Adjunta de Planes y Proyectos para el proyecto de sistemas constructivos en puentes ferroviarios de hormigón.

Descargar (PDF, 105KB)

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Clasificación de los sistemas de encofrado

Figura 1. Encofrados verticales. By Farina Destil (Farina Destil) [Public domain], via Wikimedia Commons

Se pueden clasificar los encofrados de muy distintas formas: atendiendo al material con el que están elaborados, al sistema de transmisión de cargas, al sistema de ejecución, etc. Sin embargo, se suelen agrupar en función de la posición del elemento que se va a encofrar: sistemas horizontales y sistemas verticales. Ejemplo del primer tipo son los forjados utilizados en edificación; en cuanto a los segundos, podrían ser aquellos utilizados en pilares o muros.

En cuanto a los materiales, si bien hasta hace pocas fechas era habitual el uso de la madera, nuevos materiales como el aluminio (con este material hay que tener precauciones, ver artículo 68.3 de la EHE-08) o el plástico han permitido estandarizar e industrializar más los procedimientos constructivos. Esta industrialización ha permitido reducir los tiempos de montaje y desmontaje, y con ello el periodo de ejecución de estas tareas. En una entrada anterior ya se realizó una introducción sobre lo que son y para qué sirven los encofrados.

Por tanto, como podemos ver, existen una serie de factores a tener en cuenta a la hora de elegir el mejor encofrado. Al aspecto económico habría que añadir otros que influyen directamente en él como es el tiempo de desencofrado, el coste de los elementos auxiliares, el coste de la mano de obra necesaria, la colocación y desencofrado, los equipos necesarios, el número de usos que se le de a los materiales y el coste del acabado de las superficies de hormigón.

A continuación he elaborado un mapa conceptual (Figura 2) para clarificar la clasificación de los sistemas de encofrado. Como podéis ver, además de la posición del elemento a encofrar, se ha considerado la transmisión de cargas y la ejecución del elemento para establecer un esquema que simplifique la comprensión de los sistemas.

Figura 2. Mapa conceptual de los sistemas de encofrado. Elaboración: V. Yepes

Los encofrados horizontales, normalmente empleados en forjados de edificación o losas de puentes, presentan tres grupos de elementos constituyentes (Figura 3):

Una superficie encofrante, que da la textura y que permite la transmisión de las cargas
Una estructura horizontal formada por vigas, sopandas o correas, que traslada las cargas de la superficie encofrante a la estructura vertical
Una estructura vertical, formada por puntales, que transmite las cargas a los forjados inferiores o al terreno.

Figura 3. Encofrado de forjado. Fuente: https://www.grupomaq.es/encofrado-de-forjado/

Los sistemas de encofrado vertical, típico en la ejecución de pilares y muros. Según el modo de transmisión de los esfuerzos, se clasifican a su vez en encofrados “a una cara” y encofrados “a dos caras”. Los encofrados a una cara son aquellos en los que, o bien las dos caras encofrantes se unen por tierantes, o no existe una de las caras. En este caso las presiones del hormigón fresco se absorben por estructuras externas al encofrado. En el caso del encofrado a dos caras, las presiones del hormigón se absorben por tirantes internos que atan las dos caras encofrantes. Presentan agrupaciones de elementos (Figura 4):

El sistema encofrante, que da textura y soporta la presión del hormigón fresco
La estructura de soporte, constituida por un marco exterior y unas costillas interiores de refuerzo

Figura 4. Encofrado para muros con vigas. Fuente: https://www.peri.es/productos/encofrados/encofrados-para-muros/vario-gt-24-girder-wall-formwork.html#&gid=1&pid=1

En el caso de encofrados verticales de grandes alturas, se pueden utilizar los encofrados trepantes o autotrepantes y los deslizantes. De ellos ya se ha hablado en otros posts anteriores.

Por último, os dejo un pequeño vídeo explicativo donde se resumen los aspectos más significativos de las tipologías de los encofrados.

Referencia:

MARTÍ, J.V.; YEPES, V.; GONZÁLEZ, F. (2004). Temas de procedimientos de construcción. Cimbras, andamios y encofrados. Editorial de la Universidad Politécnica de Valencia. Ref. 2004.441.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

¿Existen “playas inteligentes” en España? Hacia la playa 4.0

Mucho se está hablando sobre el concepto de “playa inteligente” o “smart beach”. Sobre este tema ya impartí una conferencia en el XVIII Foro Internacional de Turismo de Benidorm, celebrado en octubre del 2016. La respuesta es un no rotundo. Sin embargo, parece que algo se está avanzando en este sentido. Hay quien bautiza este concepto como playa 4.0, pero mucho me temo que es una vuelta de tuerca más en el ámbito del marketing para vender más de lo mismo.

Sobre este mismo tema me han invitado a impartir una conferencia magistral en el III Congreso Internacional de Calidad Ambiental en Playas Turísticas, organizado por la Universidad de la Guajira en Colombia, del que también formo parte del Comité Científico Internacional. Dicho congreso se celebra entre el 21 y el 23 de marzo de 2018. Debido a problemas de agenda, se me invitó a impartir la charla por teleconferencia. Para evitar problemas técnicos, he grabado dicha comunicación y os la paso para que tengáis acceso a dicha información. Espero que os sea de interés.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Construcción de puentes mediante autocimbra bajo tablero

La cimbra autolanzable bajo tablero constituye, hoy en día, el proceso constructivo de autocimbra más habitual. Entre sus ventajas se encuentra la facilidad a la hora de variar el peralte o adaptarse a acuerdos verticales y curvas en planta; además, se libera la parte superior, lo que permite la introducción de ferralla prefabricada y el resto de materiales. Alguno de sus inconvenientes pasan por necesitar cierta altura libre mínima (7-12 m) bajo cabeza de pilas y que son más deformables que las cimbras autolanzables sobre tablero.

Os dejo a continuación un pequeño vídeo explicativo de este tipo de procedimiento constructivo. Espero que os sea de interés.

En el siguiente vídeo de Mecanotubo se puede ver, con todo detalle, una animación en 3D que describe con claridad el procedimiento.

A continuación podemos ver un vídeo realizado por voxelestudios del proceso constructivo del tablero de los viaductos de Contreras, que con autocimbras se ejecutaron tramos de luces de 66 m.

Referencias:

MARTÍ, J.V.; YEPES, V.; GONZÁLEZ, F. (2004). Temas de procedimientos de construcción. Cimbras, andamios y encofrados. Editorial de la Universidad Politécnica de Valencia. Ref. 2004.441.

SEOPAN (2015). Manual de cimbras autolanzables. Tornapunta Ediciones, Madrid, 359 pp.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Construcción de puentes mediante cimbra autolanzable sobre tablero

A.T. AVE NORTE-NOROESTE: NUDO VENTA BAÑOS 01. http://www.ar2v.com

Las cimbras autolanzables, también llamadas autocimbras o cimbras de avance, se utilizan para el hormigonado de tableros de puentes o viaductos vano a vano. Son capaces de trasladarse a lo largo del puente por sus propios medios (“cimbras-máquina”). En el caso de las cimbras autolanzables sobre tablero, se solucionan algunos problemas como los gálibos estrictos o la posibilidad de utilizar la cimbra como carril de rodadura de un pórtico grúa que lleve los materiales y medios auxiliares. Sin embargo es una estructura más pesada y compleja, de mayor coste y dificultad de montaje y maniobra, por lo que no es tan habitual su uso como en el caso de autocimbras bajo tablero.

A continuación os dejo un Polimedia explicativo sobre este medio auxiliar, que espero que os sea de interés.

Os dejo un vídeo sobre una cimbra autolanzable de una luz de 90 m.

Referencias:

SEOPAN (2015). Manual de cimbras autolanzables. Tornapunta Ediciones, Madrid, 359 pp.

Construcción de puentes mediante lanzador de vigas

Cuando no es posible el uso de grúas, se puede recurrir a los lanzadores de vigas, vigas de lanzamiento o cimbras autolanzables. Se trata de un procedimiento excepcional debido a su compleja puesta en obra y a su baja productividad. Se emplean si el ritmo de llegada de las vigas a obra es pequeño, por ejemplo un par de vigas al día. Las vigas de lanzamiento requieren personal especializado en su manejo y montaje debido a que los movimientos son complejos y los esfuerzos generados pueden comprometer la estabilidad del conjunto. Estos problemas se complican cuando la rasante vertical del puente presenta acuerdos de radios menores a 12000 m, en cuyo caso la viga se apoya en tres puntos, con sus consiguientes esfuerzos hiperestáticos.

Lanzador de vanos completos. http://www.weiku.com

Las vigas de lanzamiento cubren luces entre 35 y 75 m, con pesos entre 600 kN y 4500 kN y pendientes máximas para el lanzamiento del 5%. Constan de dos vigas reticuladas unidas en sus extremidades sobre las que rueda el tren de los cabrestantes, compuesto por dos carros para elevar la viga a lanzar y un tercero para el desplazamiento longitudinal de la viga y el armazón. Las vigas prefabricadas se transportan desde el acopio al lanzador mediante carros elefante. Téngase en cuenta que los carros pueden moverse a velocidades de 5 km/h mientras que el lanzador solo alcanza los 3 m/minuto.

Os paso a continuación una pequeña presentación que he preparado para explicar este procedimiento constructivo de puentes. También os paso algún vídeo más al respecto que espero os resulten interesantes.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Optimización heurística mediante aceptación por umbrales

En algunos posts anteriores hemos comentado lo que es un modelo matemático de optimización, qué son las metaheurísticas, o cómo poder optimizar las estructuras de hormigón. A continuación os presentamos un Polimedia donde se explica brevemente cómo podemos optimizar siguiendo la técnica de optimización heurística mediante aceptación por umbrales. Podréis comprobar cómo se trata de un caso similar a la famosa técnica de la cristalización simulada. Espero que os sea útil.

Podéis consultar, a modo de ejemplo, algunos artículos científicos que hemos escrito a ese respecto en las siguientes publicaciones:

CARBONELL, A.; GONZÁLEZ-VIDOSA, F.; YEPES, V. (2011). Heuristic optimization of reinforced concrete road vault underpasses. Advances in Engineering Software, 42(4): 151-159. ISSN: 0965-9978. (link)
MARTÍNEZ, F.J.; GONZÁLEZ-VIDOSA, F.; HOSPITALER, A.; YEPES, V. (2010). Heuristic Optimization of RC Bridge Piers with Rectangular Hollow Sections. Computers & Structures, 88: 375-386. ISSN: 0045-7949. (link)
YEPES, V.; MEDINA, J.R. (2006). Economic Heuristic Optimization for Heterogeneous Fleet VRPHESTW. Journal of Transportation Engineering, ASCE, 132(4): 303-311. (link)

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

¿Qué es la optimización por cristalización simulada?

La cristalización simulada (también llamado recocido simulado) “Simulated Annealing, SA” constituye una de las estrategias a las que se recurre en la resolución de los problemas de optimización combinatoria. Kirkpatrick, Gelatt y Vecchi la propusieron por primera vez en 1983 y Cerny en 1985 de forma independiente. Estos autores se inspiraron en los trabajos sobre Mecánica Estadística de Metrópolis et al. (1953). La metaheurística despliega una estructura que se inserta cómodamente en la programación, mostrando además una considerable habilidad para escapar de los óptimos locales. Fue una técnica que experimentó un auge considerable en la década de los 80 para resolver los modelos matemáticos de optimización.

La energía de un sistema termodinámico se compara con la función de coste evaluada para una solución admisible de un problema de optimización combinatoria. En ambos casos se trata de evolucionar de un estado a otro de menor energía o coste. El acceso de un estado metaestable a otro se alcanza introduciendo “ruido” con un parámetro de control al que se denomina temperatura. Su reducción adecuada permite, con una elevada probabilidad, que un sistema termodinámico adquiera un mínimo global de energía. Conceptualmente es un algoritmo de búsqueda por entornos, que selecciona candidatos de forma aleatoria. La alternativa se aprueba si perfecciona la solución actual (D menor o igual que cero); en caso contrario, será aceptada con una probabilidad (e^(-^D/T) si D>0, donde T es el parámetro temperatura) decreciente con el aumento de la diferencia entre los costes de la solución candidata y la actual. El proceso se repite cuando la propuesta no es admitida. La selección aleatoria de soluciones degradadas permite eludir los mínimos locales. La cristalización simulada se codifica fácilmente, incluso en problemas complejos y con funciones objetivo arbitrarias. Además, con independencia de la solución inicial, el algoritmo converge estadísticamente a la solución óptima (Lundy y Mees, 1986). En cualquier caso, SA proporciona generalmente soluciones valiosas, aunque no informa si ha llegado al óptimo absoluto. Por contra, al ser un procedimiento general, en ocasiones no resulta competitivo, aunque sí comparable, ante otros específicos que aprovechan información adicional del problema. El algoritmo es lento, especialmente si la función objetivo es costosa en su tiempo de computación. Además, la cristalización simulada pierde terreno frente a otros métodos más simples y rápidos como el descenso local cuando el espacio de las soluciones es poco abrupto o escasean los mínimos locales.

Os dejo un vídeo explicativo:

Referencias

CERNY, V. (1985). Thermodynamical approach to the traveling salesman problem: an efficient simulated algorithm. Journal of Optimization Theory and Applications, 45: 41-51.

KIRKPATRICHK, S.; GELATT, C.D.; VECCHI, M.P. (1983). Optimization by simulated annealing. Science, 220(4598): 671-680.

LUNDY, M.; MEES, A. (1986). Convergence of an Annealing Algorithm. Mathematical programming, 34:111-124.

METROPOLIS, N.; ROSENBLUTH, A.W.; ROSENBLUTH, M.N.; TELLER, A.H.; TELER, E. (1953). Equation of State Calculation by Fast Computing Machines. Journal of Chemical Physics, 21:1087-1092.

GONZÁLEZ-VIDOSA-VIDOSA, F.; YEPES, V.; ALCALÁ, J.; CARRERA, M.; PEREA, C.; PAYÁ-ZAFORTEZA, I. (2008) Optimization of Reinforced Concrete Structures by Simulated Annealing. TAN, C.M. (ed): Simulated Annealing. I-Tech Education and Publishing, Vienna, pp. 307-320. (link)

¿Es fácil optimizar estructuras de hormigón?

Es más, ¿es posible que un ordenador sea capaz de diseñar de forma automática estructuras óptimas sin darle ninguna pista o información previa? Estoy convencido que a la vuelta de un par de años, todos los programas comerciales tendrán paquetes de optimización estructural que permitirán reducciones de coste en torno al 5-15% respecto a los programas actuales. Ya os adelanto que esta nueva tecnología va a traer consigo nuevas patologías en las estructuras de hormigón, que con la optimización se parecen más a las estructuras metálicas. Con el tiempo habrá que introducir capítulos o restricciones en las futuras versiones de la EHE o de los Eurocódigos. En este post vamos a continuar comentando aspectos relacionados con la modelización matemática, la optimización combinatoria, las metaheurísticas y los algoritmos.

Toda esta aventura la empezamos en el año 2002, con el primer curso de doctorado sobre optimización heurística en la ingeniería civil, que luego hemos ido ampliando y mejorando en el actual Máster Oficial en Ingeniería del Hormigón. Ya tenemos varias tesis doctorales y artículos científicos al respecto para aquellos de vosotros curiosos o interesados en el tema. Para aquellos que queráis ver algunas aplicaciones concretas, os recomiendo el siguiente capítulo de libro que escribimos sobre la optimización de distintas estructuras con un algoritmo tan simple como la cristalización simulada. Para aquellos otros que tengáis más curiosidad, os dejo algunas publicaciones de nuestro grupo de investigación en el apartado de referencias.

Os paso, para abrir boca, una forma sencilla de optimizar a través de este Polimedia. Espero que os guste.

Referencias:

MOLINA-MORENO, F.; MARTÍ, J.V.; YEPES, V. (2017). Carbon embodied optimization for buttressed earth-retaining walls: implications for low-carbon conceptual designs. Journal of Cleaner Production, 164:872-884. https://authors.elsevier.com/a/1VLOP3QCo9NDzg
GARCÍA-SEGURA, T.; YEPES, V.; FRANGOPOL, D.M.; YANG, D.Y. (2017). Lifetime Reliability-Based Optimization of Post-Tensioned Box-Girder Bridges. Engineering Structures, 145:381-391. DOI:10.1016/j.engstruct.2017.05.013 OPEN ACCESS
GARCÍA-SEGURA, T.; YEPES, V.; FRANGOPOL, D.M. (2017). Multi-Objective Design of Post-Tensioned Concrete Road Bridges Using Artificial Neural Networks. Structural and Multidisciplinary Optimization, 56(1):139-150. doi: 10.1007/s00158-017-1653-0
YEPES, V.; MARTÍ, J.V.; GARCÍA-SEGURA, T.; GONZÁLEZ-VIDOSA, F. (2017). Heuristics in optimal detailed design of precast road bridges. Archives of Civil and Mechanical Engineering, 17(4):738-749. DOI: 10.1016/j.acme.2017.02.006
MOLINA-MORENO, F.; GARCÍA-SEGURA; MARTÍ, J.V.; YEPES, V. (2017). Optimization of Buttressed Earth-Retaining Walls using Hybrid Harmony Search Algorithms. Engineering Structures, 134:205-216. DOI: 10.1016/j.engstruct.2016.12.042
GARCÍA-SEGURA, T.; YEPES, V. (2016). Multiobjective optimization of post-tensioned concrete box-girder road bridges considering cost, CO2 emissions, and safety. Engineering Structures, 125:325-336. DOI: 10.1016/j.engstruct.2016.07.012.
MARTÍ, J.V.; GARCÍA-SEGURA, T.; YEPES, V. (2016). Structural design of precast-prestressed concrete U-beam road bridges based on embodied energy. Journal of Cleaner Production, 120:231-240. DOI: 10.1016/j.jclepro.2016.02.024
GARCÍA-SEGURA, T.; YEPES, V.; ALCALÁ, J.; PÉREZ-LÓPEZ, E. (2015). Hybrid harmony search for sustainable design of post-tensioned concrete box-girder pedestrian bridges. Engineering Structures, 92:112-122. DOI: 10.1016/j.engstruct.2015.03.015 (link)
LUZ, A.; YEPES, V.; GONZÁLEZ-VIDOSA, F.; MARTÍ, J.V. (2015). Diseño de estribos abiertos en puentes de carretera obtenidos mediante optimización híbrida de escalada estocástica. Informes de la Construcción, 67(540), e114. DOI: 10.3989/ic.14.089
MARTÍ, J.V.; YEPES, V.; GONZÁLEZ-VIDOSA, F. (2015). Memetic algorithm approach to designing of precast-prestressed concrete road bridges with steel fiber-reinforcement. Journal of Structural Engineering ASCE, 141(2): 04014114. DOI:10.1061/(ASCE)ST.1943-541X.0001058 (descargar versión autor)
YEPES, V.; GARCÍA-SEGURA, T.; MORENO-JIMÉNEZ, J.M. (2015). A cognitive approach for the multi-objective optimization of RC structural problems. Archives of Civil and Mechanical Engineering, 15(4):1024-1036. doi:10.1016/j.acme.2015.05.001
YEPES, V.; MARTÍ, J.V.; GARCÍA-SEGURA, T. (2015). Cost and CO2 emission optimization of precast-prestressed concrete U-beam road bridges by a hybrid glowworm swarm algorithm. Automation in Construction, 49:123-134. DOI: 10.1016/j.autcon.2014.10.013 (link)
GARCÍA-SEGURA, T.; YEPES, V.; MARTÍ, J.V.; ALCALÁ, J. (2014). Optimization of concrete I-beams using a new hybrid glowworm swarm algorithm. Latin American Journal of Solids and Structures, 11(7):1190 – 1205. ISSN: 1679-7817. (link)
MARTÍ, J.V.; YEPES, V.; GONZÁLEZ-VIDOSA, F.; LUZ, A. (2013). Diseño automático de tableros óptimos de puentes de carretera de vigas artesa prefabricadas mediante algoritmos meméticos híbridos. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, DOI: http://dx.doi.org/10.1016/j.rimni.2013.04.010.
TORRES-MACHÍ, C.; YEPES, V.; ALCALA, J.; PELLICER, E. (2013). Optimization of high-performance concrete structures by variable neighborhood search. International Journal of Civil Engineering, 11(2):90-99 . ISSN: 1735-0522. (link)
MARTÍNEZ-MARTÍN, F.; GONZÁLEZ-VIDOSA, F.; HOSPITALER, A.; YEPES, V. (2013). A parametric study of optimum tall piers for railway bridge viaducts. Structural Engineering and Mechanics, 45(6): 723-740. (link)
MARTINEZ-MARTIN, F.J.; GONZALEZ-VIDOSA, F.; HOSPITALER, A.; YEPES, V. (2012). Multi-objective optimization design of bridge piers with hybrid heuristic algorithms. Journal of Zhejiang University-SCIENCE A (Applied Physics & Engineering, 13(6):420-432. DOI: 10.1631/jzus.A1100304. ISSN 1673-565X (Print); ISSN 1862-1775 (Online). (link)
MARTÍ, J.V.; GONZÁLEZ-VIDOSA, F.; YEPES, V.; ALCALÁ, J. (2013). Design of prestressed concrete precast road bridges with hybrid simulated annealing. Engineering Structures, 48:342-352. DOI:10.1016/j.engstruct.2012.09.014. ISSN: 0141-0296.(link)
YEPES, V.; GONZÁLEZ-VIDOSA, F.; ALCALÁ, J.; VILLALBA, P. (2012). CO₂-Optimization Design of Reinforced Concrete Retaining Walls based on a VNS-Threshold Acceptance Strategy. Journal of Computing in Civil Engineering ASCE, 26 (3):378-386. DOI: 10.1061/(ASCE)CP.1943-5487.0000140. ISNN: 0887-3801. (link)
CARBONELL, A.; YEPES, V.; GONZÁLEZ-VIDOSA, F. (2011). Búsqueda exhaustiva por entornos aplicada al diseño económico de bóvedas de hormigón armado. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, 27(3):227-235. (link) [Global best local search applied to the economic design of reinforced concrete vauls]
CARBONELL, A.; GONZÁLEZ-VIDOSA, F.; YEPES, V. (2011). Heuristic optimization of reinforced concrete road vault underpasses. Advances in Engineering Software, 42(4): 151-159. ISSN: 0965-9978. (link)
MARTÍNEZ, F.J.; GONZÁLEZ-VIDOSA, F.; HOSPITALER, A. (2011). Estudio paramétrico de pilas para viaductos de carretera. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, 27(3):236-250. (link)
MARTÍNEZ, F.J.; GONZÁLEZ-VIDOSA, F.; HOSPITALER, A.; ALCALÁ, J. (2011). Design of tall bridge piers by ant colony optimization. Engineering Structures, 33:2320-2329.
PEREA, C.; YEPES, V.; ALCALÁ, J.; HOSPITALER, A.; GONZÁLEZ-VIDOSA, F. (2010). A parametric study of optimum road frame bridges by threshold acceptance. Indian Journal of Engineering & Materials Sciences, 17(6):427-437. ISSN: 0971-4588. (link)
PAYÁ-ZAFORTEZA, I.; YEPES, V.; GONZÁLEZ-VIDOSA, F.; HOSPITALER, A. (2010). On the Weibull cost estimation of building frames designed by simulated annealing. Meccanica, 45(5): 693-704. DOI 10.1007/s11012-010-9285-0. ISSN: 0025-6455. (link)
MARTÍ, J.V.; GONZÁLEZ-VIDOSA, F. (2010). Design of prestressed concrete precast pedestrian bridges by heuristic optimization. Advances in Engineering Software, 41(7-8): 916-922. http://dx.doi.org/10.1016/j.advengsoft.2010.05.003
MARTÍNEZ, F.J.; GONZÁLEZ-VIDOSA, F.; HOSPITALER, A.; YEPES, V. (2010). Heuristic Optimization of RC Bridge Piers with Rectangular Hollow Sections. Computers & Structures, 88: 375-386. ISSN: 0045-7949. (link)
PAYÁ, I.; YEPES, V.; HOSPITALER, A.; GONZÁLEZ-VIDOSA, F. (2009). CO₂-Efficient Design of Reinforced Concrete Building Frames. Engineering Structures, 31: 1501-1508. ISSN: 0141-0296. (link)
YEPES, V.; ALCALÁ, J.; PEREA, C.; GONZÁLEZ-VIDOSA, F. (2008). A Parametric Study of Optimum Earth Retaining Walls by Simulated Annealing. Engineering Structures, 30(3): 821-830. ISSN: 0141-0296. (link)
PEREA, C.; ALCALÁ, J.; YEPES, V.; GONZÁLEZ-VIDOSA, F.; HOSPITALER, A. (2008). Design of Reinforced Concrete Bridge Frames by Heuristic Optimization. Advances in Engineering Software, 39(8): 676-688. ISSN: 0965-9978. (link)
PAYÁ, I.; YEPES, V.; GONZÁLEZ-VIDOSA, F.; HOSPITALER, A. (2008). Multiobjective Optimization of Reinforced Concrete Building Frames by Simulated Annealing. Computer-Aided Civil and Infrastructure Engineering, 23(8): 596-610. ISSN: 1093-9687. (link)
PAYÁ, I.; YEPES, V.; CLEMENTE, J.J.; GONZÁLEZ-VIDOSA, F. (2006). Optimización heurística de pórticos de edificación de hormigón armado. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, 22(3): 241-259. [Heuristic optimization of reinforced concrete building frames]. (link)