Etiqueta: simulated annealing

Optimización heurística mediante recocido simulado (simulated annealing)

El recocido simulado (simulated annealing, SA) es una técnica metaheurística estocástica potente diseñada para abordar problemas de optimización global en espacios de búsqueda grandes y complejos. Inspirado en el proceso de recocido de la metalurgia, el algoritmo explora ampliamente el espacio de soluciones a «temperaturas» elevadas y se centra gradualmente en las regiones más prometedoras a medida que la temperatura desciende. Su característica distintiva es la capacidad de aceptar soluciones peores con una probabilidad que disminuye con el tiempo, lo que le permite escapar de mínimos locales y evitar la convergencia prematura.

Este método es particularmente eficaz para problemas NP-hard, como el problema del viajante, la planificación de tareas y el diseño de circuitos, en los que los algoritmos exactos resultan inviables desde el punto de vista computacional. Aunque el SA no garantiza la obtención del óptimo global, produce soluciones de alta calidad en tiempos de cálculo prácticos de forma consistente. El éxito del algoritmo depende en gran medida del ajuste preciso de sus parámetros, como la temperatura inicial, el esquema de enfriamiento y la longitud de las iteraciones en cada nivel de temperatura. Su robustez y versatilidad lo han consolidado como una herramienta fundamental en campos tan diversos como la ingeniería estructural, la química molecular, el procesamiento de imágenes y la asignación de recursos.

Principios fundamentales y origen

El recocido simulado (SA), también conocido como templado simulado, recristalización simulada o enfriamiento simulado, es una técnica metaheurística que adapta un proceso físico al ámbito de la optimización.

  • Definición: El SA es un método estocástico de optimización global. Su estrategia se basa en la analogía con el recocido metalúrgico, proceso en el que un material se calienta y luego se enfría de forma controlada para alcanzar una estructura cristalina estable y de baja energía.
  • Mecanismo central: El algoritmo mejora las soluciones de forma iterativa. Acepta incondicionalmente las soluciones candidatas que son mejores que la actual y, con una probabilidad decreciente, también acepta movimientos que la empeoran. Esta aceptación controlada de transiciones «cuesta arriba» es clave para evitar quedar atrapado en óptimos locales y para permitir un cambio gradual de la exploración a la explotación del espacio de soluciones.
  • Origen: El SA fue desarrollado de forma independiente por Kirkpatrick, Gelatt y Vecchi (1983) y por Černý (1985). Su base teórica se encuentra en el algoritmo de Metropolis (1953), que se aplicó originalmente a la simulación de sistemas termodinámicos.

Mecanismo de funcionamiento y analogía termodinámica.

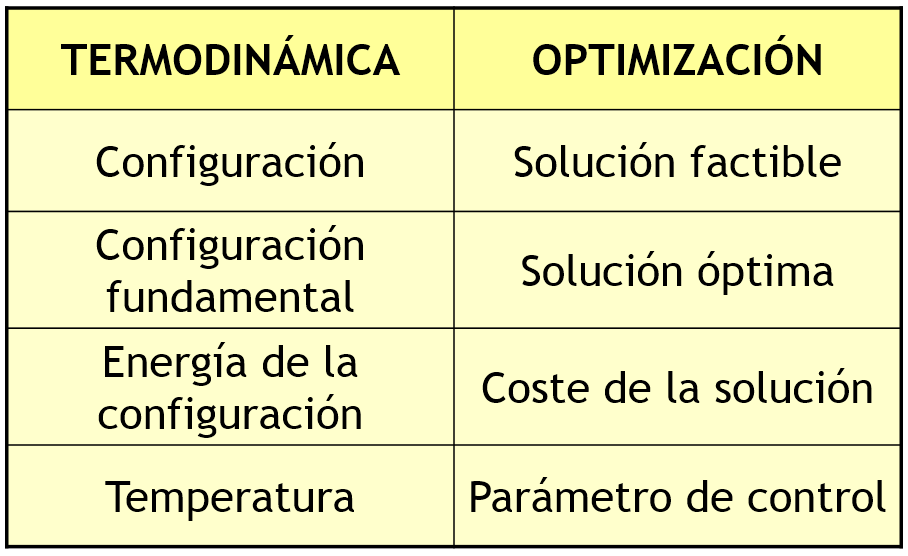
El SA establece un paralelismo directo entre la optimización y la termodinámica estadística, donde los conceptos se relacionan de la siguiente manera:

  • Función objetivo: corresponde a la energía de un sistema físico. El objetivo es minimizar dicha energía.
  • Solución óptima: representa una estructura cristalina de baja energía, que es un estado estable del sistema.
  • Temperatura (T): Es el parámetro que regula el comportamiento estocástico. A altas temperaturas, el sistema es más volátil y explora más; a bajas, se estabiliza.

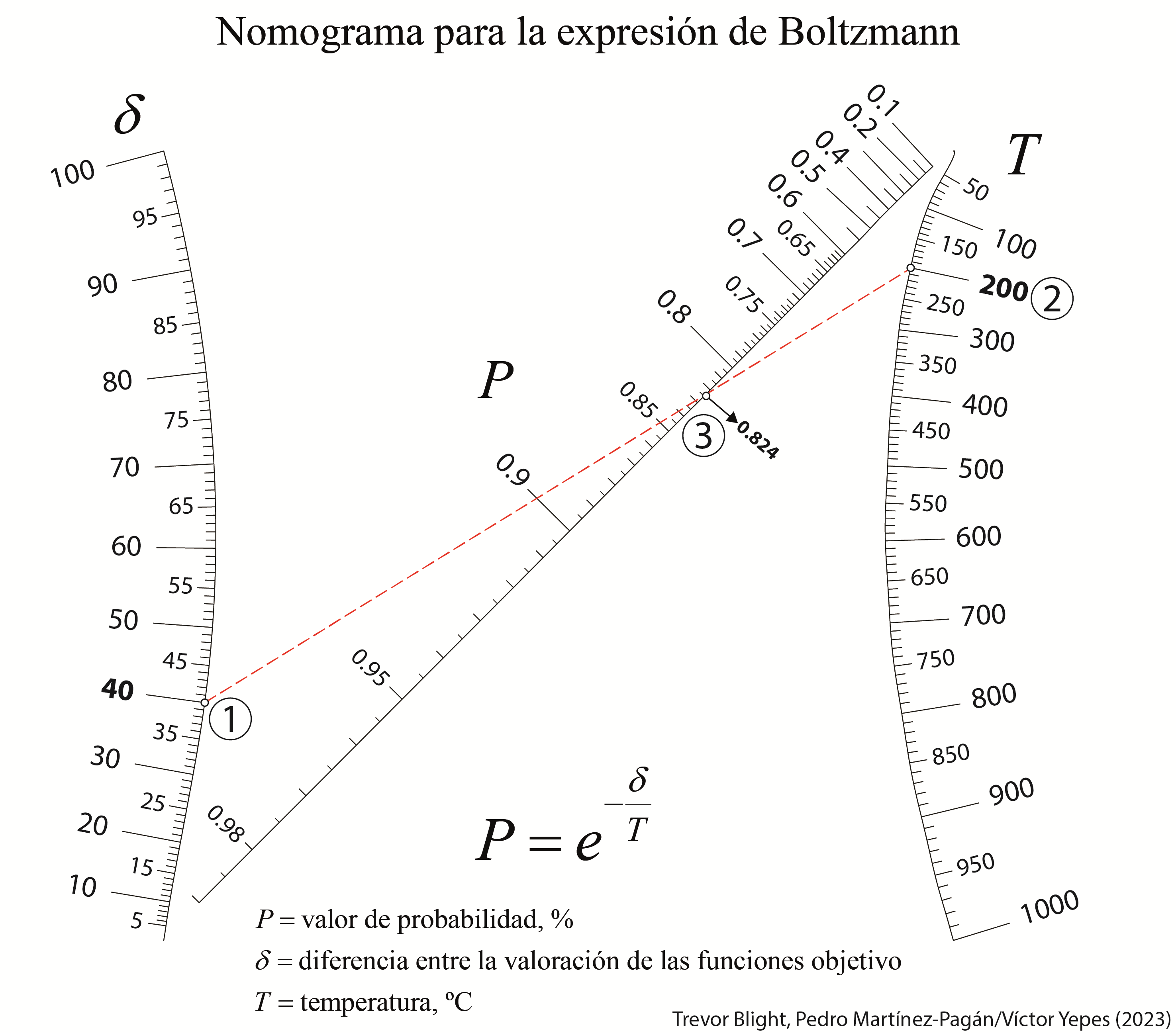
El proceso de optimización se rige por el factor de Boltzmann, exp(-ΔE/T), donde ΔE es el cambio en la energía (valor de la función objetivo) de la nueva configuración y T es la temperatura actual.

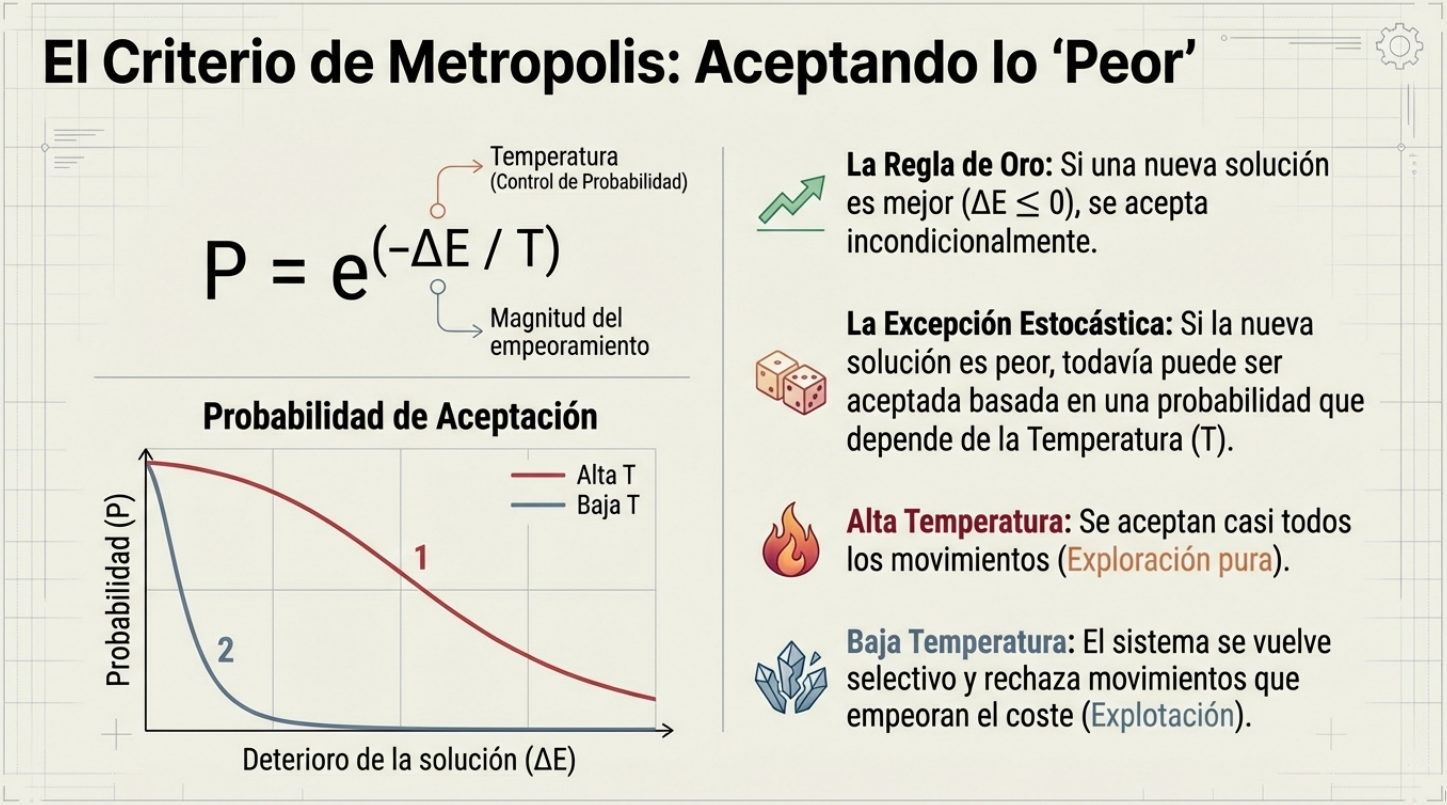
El criterio de aceptación de una nueva solución s' a partir de una solución actual s sigue la regla de Metropolis:

  1. Si el cambio de energía ΔE = f(s') - f(s) es menor o igual a cero (ΔE ≤ 0), la nueva solución es mejor o igual, por lo que se acepta siempre.
  2. Si el cambio de energía es positivo (ΔE > 0), la nueva solución es peor. Se acepta con una probabilidad P = exp(-ΔE/T).

Esta probabilidad es alta a temperaturas elevadas, lo que fomenta la diversificación y la exploración global. A medida que T se acerca a cero, la probabilidad de aceptar malos movimientos disminuye drásticamente, haciendo que el algoritmo sea más selectivo y se comporte de manera “codiciosa” (greedy), intensificando la búsqueda en regiones prometedoras.

Componentes clave del algoritmo

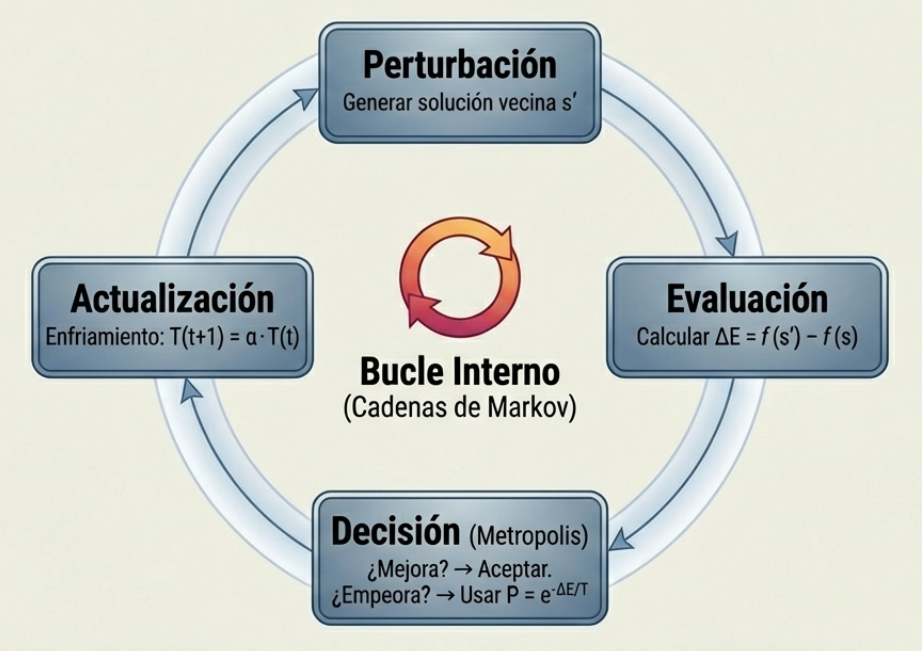
El rendimiento del SA depende de la calibración precisa de su «esquema de enfriamiento». Sus componentes matemáticos y de procedimiento clave son los siguientes:

Componente Descripción
Temperatura inicial (T₀) Se elige un valor lo suficientemente alto como para asegurar una alta probabilidad de aceptación inicial, lo que permite una exploración amplia del espacio de soluciones. El método de Medina (2001) sugiere ajustarla para que la tasa de aceptación de soluciones de mayor coste se sitúe entre el 20% y el 40%.
Esquema de enfriamiento Define cómo disminuye la temperatura. El más común es el esquema geométrico: T(t+1) = α * Tt, donde α es un coeficiente de reducción típicamente en el rango de [0.8, 0.99]. Una refrigeración rápida corre el riesgo de atrapar la solución en estados metaestables, mientras que una lenta mejora la fiabilidad a un mayor coste computacional.
Longitud de la cadena de Markov Es el número de iteraciones que se ejecutan en cada nivel de temperatura. Debe ser lo suficientemente largo como para que el sistema alcance un estado de equilibrio a esa temperatura antes de seguir enfriando.
Criterio de parada Determina cuándo finaliza el algoritmo. Las condiciones comunes incluyen que la temperatura caiga por debajo de un umbral predefinido (p. ej., el 1% de la temperatura inicial) o que las mejoras en la solución se estabilicen.

Variantes y mejoras

Con el fin de mejorar la eficiencia y la adaptabilidad del SA, se han desarrollado diversas variantes y modificaciones.

  • Estrategia “Best-So-Far”: Mantiene en memoria la mejor solución encontrada hasta el momento, independientemente del estado actual de la búsqueda.
  • Esquemas de recalentamiento: Cuando el sistema se estanca en un óptimo local, la temperatura se incrementa temporalmente para promover una nueva fase de exploración (Dowsland, 1993).
  • Hibridación: Se integra el SA con otros métodos, como algoritmos genéticos, branch-and-bound o programación entera, para aprovechar sus fortalezas complementarias.
  • Implementaciones paralelas: Distribuyen los ensayos entre múltiples procesadores para mejorar la escalabilidad y la velocidad de convergencia.
  • Evaluaciones aproximadas de ΔE: Se utilizan en problemas de alta dimensionalidad para acelerar el cálculo.

Threshold Accepting (TA)

Una variante notable es el Threshold Accepting (TA), introducido por Dueck y Scheuer en 1990. Este método sustituye la regla de aceptación probabilística por una regla determinista: se acepta una solución subóptima si su empeoramiento es inferior a un umbral predefinido.

  • Se acepta una solución subóptima si su empeoramiento (degradación) es inferior a un umbral predefinido.
    Este umbral disminuye gradualmente durante la búsqueda, de forma análoga al esquema de enfriamiento del SA.

Estudios empíricos han demostrado que el TA puede tener un rendimiento comparable o incluso superior al del SA en problemas de planificación, programación y asignación de recursos (Lin et al., 1995).

Dominios de aplicación y ejemplos notables

El SA ha demostrado ser una herramienta versátil y fiable, especialmente para problemas NP-hard para los que no existen solucionadores específicos.

Dominio Aplicación específica y referencia
Enrutamiento Resolución del Problema del Viajante de Comercio (TSP) y sus variantes con restricciones de tiempo (Kirkpatrick et al., 1983).
Planificación Solución de problemas de job-shop scheduling mediante un equilibrio entre diversificación e intensificación (van Laarhoven et al., 1992).
Asignación de recursos Manejo de la complejidad del Problema de Asignación Cuadrática (QAP) en el diseño de instalaciones (Connolly, 1990).
Procesamiento de imágenes Métodos de relajación estocástica para resolver problemas de segmentación y restauración de imágenes (Geman y Geman, 1984).
Química molecular Herramienta estándar para la cristalografía macromolecular y el refinamiento conformacional (Brünger, 1992).
Ingeniería estructural – Diseño de puentes de hormigón pretensado (Martí et al., 2013).

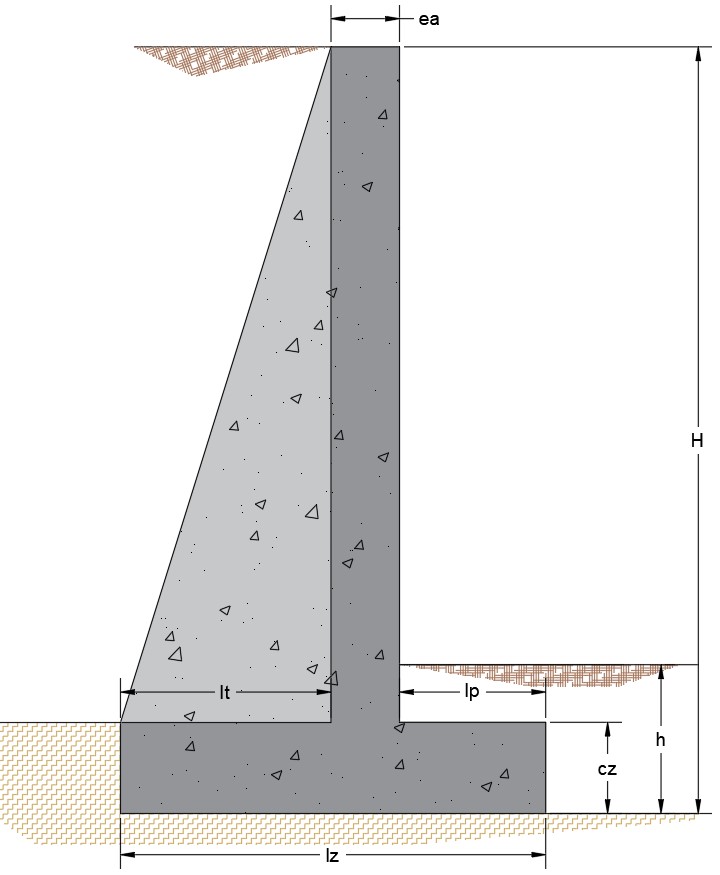
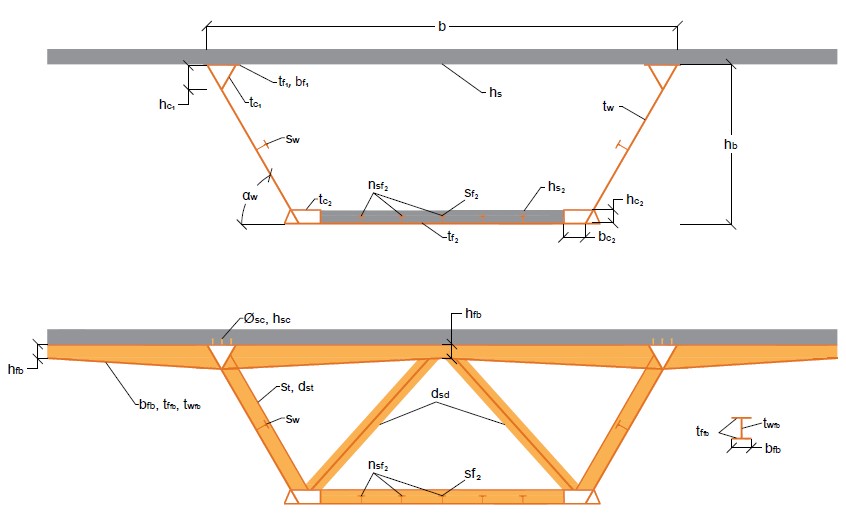
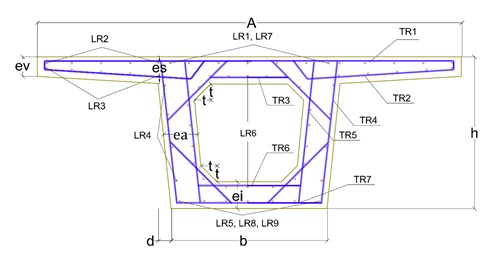
– Optimización paramétrica de muros de contención (Yepes et al., 2008).

– Optimización del tamaño y la disposición de las estructuras de acero (Bresolin et al., 2022).

– Minimización de costes e impacto ambiental (CO₂) en el hormigón armado (Santoro y Kripka, 2020; Medeiros y Kripka, 2014).

– Diseño de estructuras marinas bajo incertidumbre (Toğan, 2012).

Factores críticos para el rendimiento.

El éxito en la aplicación del SA depende en gran medida de la formulación del problema:

  1. Representación del espacio de configuración: La forma en que se define matemáticamente el espacio de soluciones es fundamental.
  2. Definición de movimientos: Es esencial elegir un conjunto adecuado de «movimientos» o ajustes que permitan pasar de una solución a otra vecina. Las representaciones efectivas aseguran que las transiciones entre mínimos locales impliquen pequeñas diferencias de coste, lo que reduce las «barreras de energía».
  3. Función objetivo: Una función objetivo bien elegida puede modificar la distribución de los mínimos locales hacia valores de menor coste promedio, lo que aumenta la probabilidad de encontrar soluciones mejores.
  4. Manejo de restricciones: En los problemas con restricciones, la búsqueda puede limitarse a regiones factibles o pueden permitirse soluciones infactibles penalizándolas en la función objetivo. Este último enfoque puede simplificar la estructura de vecindad y suavizar la topología del paisaje de búsqueda, lo que mejora la convergencia.

Os dejo un vídeo que grabé hace unos años para explicar esta metaheurística. Espero que os sea de interés.

Referencias:

Bresolin, J. M., Pravia, Z. M., & Kripka, M. (2022). Discrete sizing and layout optimization of steel truss-framed structures with Simulated Annealing Algorithm. Steel and Composite Structures, 44(5), 603–617. https://doi.org/10.12989/scs.2022.44.5.603

Brünger, A. T. (1992). X-PLOR Version 3.1: A system for X-ray crystallography and NMR. Yale University Press.

Černý, V. (1985). Thermodynamical approach to the travelling salesman problem: An efficient simulation algorithm. Journal of Optimization Theory and Applications, 45(1), 41–51. https://doi.org/10.1007/BF00940812

Connolly, D. T. (1990). An improved annealing scheme for the QAP. European Journal of Operational Research, 46(1), 93–100. https://doi.org/10.1016/0377-2217(90)90301-Q

Dowsland, K. A. (1993). Simulated annealing. In C. R. Reeves (Ed.), Modern heuristic techniques for combinatorial problems (pp. 20–69). Wiley.

Dueck, G., & Scheuer, T. (1990). Threshold accepting: A general purpose optimization algorithm appearing superior to simulated annealing. Journal of Computational Physics, 90(1), 161–175. https://doi.org/10.1016/0021-9991(90)90201-B

Geman, S., & Geman, D. (1984). Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images. IEEE Transactions on Pattern Analysis and Machine Intelligence, 6(6), 721–741. https://doi.org/10.1109/TPAMI.1984.4767596

Kirkpatrick, S., Gelatt, C. D., & Vecchi, M. P. (1983). Optimization by simulated annealing. Science, 220(4598), 671–680. https://doi.org/10.1126/science.220.4598.671

Lin, C. K. Y., Haley, K. B., & Sparks, C. (1995). A comparative study of threshold accepting and simulated annealing algorithms in three scheduling problems. European Journal of Operational Research, 83(2), 330–346. https://doi.org/10.1016/0377-2217(95)00011-E

Martí, J. V., González-Vidosa, F., Yepes, V., & Alcalá, J. (2013). Design of prestressed concrete precast road bridges with hybrid simulated annealing. Engineering Structures, 48, 342–352. https://doi.org/10.1016/j.engstruct.2012.09.014

Medeiros, F., & Kripka, M. (2014). Optimization of reinforced concrete columns according to cost and CO₂ emissions. Engineering Structures, 59, 185–194. https://doi.org/10.1016/j.engstruct.2013.10.045

Medina, J. R. (2001). Estimation of incident and reflected waves using simulated annealing. Journal of Waterway, Port, Coastal and Ocean Engineering, 127(4), 213–221. https://doi.org/10.1061/(ASCE)0733-950X(2001)127:4(213)

Metropolis, N., Rosenbluth, A. W., Rosenbluth, M. N., Teller, A. H., & Teller, E. (1953). Equation of state calculations by fast computing machines. The Journal of Chemical Physics, 21(6), 1087–1092. https://doi.org/10.1063/1.1699114

Santoro, J. F., & Kripka, M. (2020). Minimizing environmental impact in the design of reinforced concrete elements using simulated annealing. Computers and Concrete, 25(2), 111–118. https://doi.org/10.12989/cac.2020.25.2.111

Toğan, V. (2012). Optimization of monopod offshore tower under uncertainties with gradient-based and gradient-free optimization algorithms. Advances in Structural Engineering, 15(12), 2021–2032. https://doi.org/10.1260/1369-4332.15.12.2021

van Laarhoven, P. J. M., & Aarts, E. H. L. (1987). Simulated annealing: Theory and applications (Mathematics and Its Applications, Vol. 37). Springer. https://doi.org/10.1007/978-94-015-7744-1

van Laarhoven, P. J. M., Aarts, E. H. L., & Lenstra, J. K. (1992). Job shop scheduling by simulated annealing. Operations Research, 40(1), 113–125. https://doi.org/10.1287/opre.40.1.113

Yepes, V., Alcalá, J., Perea, C., & González-Vidosa, F. (2008). A parametric study of optimum earth retaining walls by simulated annealing. Engineering Structures, 30(3), 821–830. https://doi.org/10.1016/j.engstruct.2007.05.023

Yepes, V. (2026). Heuristic Optimization Using Simulated Annealing. In: Kulkarni, A.J., Mezura-Montes, E., Bonakdari, H. (eds) Encyclopedia of Engineering Optimization and Heuristics. Springer, Singapore. https://doi.org/10.1007/978-981-96-8165-5_48-1

Licencia de Creative Commons
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Analogía física y conceptos fundamentales de la metaheurística «Simulated Annealing»

Figura 1. Proceso de recocido del acero. https://www.win-therm.com.my/what-is-annealing-heat-treatment-process-annealing/

En un artículo anterior describimos la metaheurística conocida como “Recocido simulado” o “Cristalización simulada”, que en inglés se conoce como “Simulated Annealing”. Para los que no estéis familiarizados con la optimización, os dejo en este enlace una descripción de lo que son las metaheurísticas.

En la década de 1980, Kirkpatrick et al. (1983), mientras trabajaban en el diseño de circuitos electrónicos, y de manera independiente, Cerny (1985), investigando el problema del TSP (Traveling Salesman Problem), consideraron la aplicación del algoritmo de Metrópolis en algunos de los desafíos de optimización combinatoria que surgen en este tipo de diseño. Para lograrlo, creyeron que era posible establecer una analogía entre los parámetros presentes en la simulación termodinámica y aquellos que se encuentran en los métodos de optimización local. En la Figura 2 se puede ver dicha analogía.

Figura 2. Analogía entre la termodinámica y la optimización (Díaz et al., 1996)

Como se puede observar, en el ámbito de la optimización, el concepto físico de temperatura no tiene un significado literal, sino que debe ser considerado como un parámetro, T, que necesita ser ajustado. De esta manera, podemos encontrar similitudes entre los procesos que tienen lugar cuando las moléculas de una sustancia se distribuyen en diferentes niveles energéticos en busca de un equilibrio a una temperatura específica y los procesos de minimización en la optimización local (o, en el caso de maximización, de manera similar).

En el primer caso, con una temperatura fija, la distribución de las partículas sigue la distribución de Boltzmann. Por lo tanto, cuando una molécula se desplaza, su movimiento será aceptado en la simulación si esto resulta en una disminución de la energía, o con una probabilidad proporcional al factor de Boltzmann si no es así. En el contexto de la optimización, al fijar el parámetro T, introducimos una perturbación y aceptamos directamente la nueva solución si su costo disminuye, o bien con una probabilidad proporcional al “factor de Boltzmann” en caso contrario.

La clave del recocido simulado es su estrategia heurística de búsqueda local. La elección del nuevo elemento del entorno, N(s), se hace de manera aleatoria, lo que puede llevar a quedar atrapado en óptimos locales. Para evitar esto, el recocido simulado permite, con una probabilidad decreciente a medida que nos acercamos a la solución óptima, el movimiento hacia soluciones peores. Al analizar el factor de Boltzmann en función de la temperatura, observamos que a medida que esta disminuye, la probabilidad de aceptar una solución peor disminuye rápidamente.

Figura 3. Valor del factor de Boltzmann en función de la temperatura y de δ (Díaz et al., 1996)

En consecuencia, la estrategia a seguir en el recocido simulado implica comenzar con una temperatura alta. Esto permite la posibilidad de aceptar soluciones peores en las primeras etapas, cuando estamos a gran distancia del óptimo global. A medida que se avanza hacia el óptimo global, se reducirá gradualmente la temperatura, disminuyendo así la probabilidad de aceptar soluciones peores. El nombre de este algoritmo proviene del proceso metalúrgico de “recocido” utilizado, por ejemplo, para eliminar las tensiones internas en el acero laminado en frío. En este proceso, el material se somete a un calentamiento rápido y luego se enfría de manera lenta y controlada durante horas.

A continuación os dejo un nomograma, elaborado junto con los profesores Trevor Blight y Pedro Martínez Pagán, para calcular la probabilidad en función de la temperatura y de δ. Aquí también resulta sencillo comprobar cómo varía dicha probabilidad en función de los valores anteriores.

 

Os dejo también un vídeo explicativo:

Referencias

CERNY, V. (1985). Thermodynamical approach to the traveling salesman problem: an efficient simulated algorithm. Journal of Optimization Theory and Applications, 45: 41-51.

DÍAZ, A. et al. (1996). Optimización heurística y redes neuronales en dirección de operaciones e ingeniería. Editorial Paraninfo, Madrid, 235 pp.

KIRKPATRICHK, S.; GELATT, C.D.; VECCHI, M.P. (1983). Optimization by simulated annealing. Science, 220(4598): 671-680.

LUNDY, M.; MEES, A. (1986). Convergence of an Annealing Algorithm. Mathematical programming, 34:111-124.

METROPOLIS, N.; ROSENBLUTH, A.W.; ROSENBLUTH, M.N.; TELLER, A.H.; TELER, E. (1953). Equation of State Calculation by Fast Computing Machines. Journal of Chemical Physics, 21:1087-1092.

GONZÁLEZ-VIDOSA-VIDOSA, F.; YEPES, V.; ALCALÁ, J.; CARRERA, M.; PEREA, C.; PAYÁ-ZAFORTEZA, I. (2008) Optimization of Reinforced Concrete Structures by Simulated Annealing. TAN, C.M. (ed): Simulated Annealing. I-Tech Education and Publishing, Vienna, pp. 307-320. (link)

Licencia de Creative Commons
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Optimización heurística de un nuevo tipo de cercha pretensada

Acaban de publicarnos un artículo en Materials, revista indexada en el primer cuartil del JCR. En este caso se ha optimizado, mediante un algoritmo de optimización heurística, un nuevo tipo de cercha metálica pretensada. El trabajo se enmarca dentro del proyecto de investigación HYDELIFE que dirijo como investigador principal en la Universitat Politècnica de València. En este caso, se trata de una colaboración entre nuestro grupo de investigación e investigadores de Georgia.

Este artículo presenta nuevos enfoques para el cálculo, el diseño y la optimización de cerchas pretensadas con un elemento de unión. Los sistemas estructurales con grandes luces, como cerchas, vigas, pórticos, etc., están sometidos a un riesgo considerable de pérdida de capacidad de carga debido a los diferentes tipos de cargas utilizadas. Algunos métodos de diseño tradicionales definen los valores del pretensado en el elemento de unión y las fuerzas internas en los elementos de la celosía para evitar esta pérdida de capacidad de carga. Sin embargo, la precisión y los límites de la determinación de las fuerzas no son necesariamente conocidos. Los autores proponen un nuevo tipo de celosía pretensada y algunos nuevos enfoques en el proceso de diseño y cálculo para resolver estos inconvenientes. Los principales objetivos del estudio fueron diseñar una innovadora y nueva forma geométrica de celosía arqueada pretensada, que permite el desarrollo de una fuerza de pretensado de alto valor, para optimizar una nueva celosía para reducir el peso propio, aumentando la capacidad de carga en comparación con sus análogos. Durante el estudio se empleó el recocido simulado. Un nuevo avance en la optimización de la celosía arqueada pretensada sugerido por los autores reduce el peso propio y mejora la capacidad de carga de la celosía entre un 8 y un 17%, dependiendo de la luz.

Abstract:

This paper represents new approaches for calculating, designing, and optimizing prestressed arched trusses with a tie member. Structural systems with long spans, such as trusses, beams, frames, etc., are subjected to a considerable/substantial risk of losing load-carrying capacity because of the different types of loads used. Some traditional design methods define the values of prestressing force in the tie member and internal forces in the truss elements to avoid this load capacity loss. However, the accuracy and limits of the determination of the forces are not necessarily known. The authors offer a new type of prestressed arched truss and some new approaches in the design and calculation process to solve these disadvantages. The study’s main objectives were to design an innovative and new geometric form of prestressed arched truss, which allows the development of high-value prestressing force, to optimize a new truss for reducing self-weight, increasing load-carrying capacity compared to its analogs. The force, stiffness matrix, and simulated annealing methods were used during the study. A new advance to the optimization of prestressed arched truss suggested by the authors reduces the self-weight and improves the load capacity of the truss by 8–17%, depending on the span.

Keywords:

Prestressed truss; stiffness matrix method; tensile element; compressed element; optimization; simulated annealing.

Reference:

PARTSKHALADZE, G.; ALCALÁ, J.; MEDZMARIASHVILI, E.; CHAVLESHVILI, G.; SURGULADZE, B., I.; YEPES, V. (2022). Heuristic Optimization of a New Type Prestressed Arched Truss. Materials, 15(22): 8144. DOI:10.3390/ma15228144

Pincha aquí para descargar

 

 

Diseño de experimentos para la calibración de la heurística de optimización de muros de contrafuertes

Variables geométricas del muro de contrafuertes

En la actualidad, los técnicos se enfrentan al desafío de encontrar soluciones estructurales más eficientes cumpliendo con todas las restricciones de seguridad y funcionalidad. Como ayuda a este reto, surgen las técnicas de optimización heurísticas. El algoritmo aplicado en este artículo es el Recocido Simulado o Simulated Annealing (SA). La estructura sobre la que se emplea esta metodología es un muro de contrafuertes de hormigón armado de 11 metros de altura. La eficiencia del algoritmo depende de la elección de los parámetros más adecuados que lo definen. Para ello, se realiza un diseño de experimentos factorial fraccionado que permite, a través de un análisis estadístico, detectar aquellos parámetros de la heurística que más afectan al resultado de la solución obtenida.

Referencia:

MARTÍ, J.V.; MARTÍNEZ-MUÑOZ, D.; YEPES, V. (2022). Diseño de experimentos para la calibración de la heurística de optimización de muros de contrafuertes. VIII Congreso de la Asociación Española de Ingeniería Estructural ACHE. Santander, 2022, 10 pp.

Pincha aquí para descargar

Optimización de tableros de puentes mixtos con metaheurística de trayectoria

Variables de la sección transversal del puente mixto

La optimización de puentes es un problema complejo debido al gran número de variables que intervienen. En este trabajo se ha realizado la optimización de un puente mixto en cajón considerando el coste como función objetivo. Para ello se ha aplicado el Recocido Simulado (SA) como ejemplo de algoritmo basado en la búsqueda de soluciones mediante trayectorias para la optimización de la estructura. Se observa que la adición de celdas a las secciones transversales del puente mejora no sólo el comportamiento de la sección sino también los resultados de la optimización. Finalmente, se observa que el diseño propuesto de doble acción compuesta materializando losas en el ala inferior sobre apoyos, permite eliminar los rigidizadores longitudinales continuos. Este método automatiza el proceso de optimización de un diseño inicial de un puente de material compuesto, que tradicionalmente se ha basado en la propia experiencia del técnico, permitiendo alcanzar resultados de forma más eficiente.

Referencia:

MARTÍNEZ-MUÑOZ, D.; SÁNCHEZ-GARRIDO, A.J.; MARTÍ, J.V.; YEPES, V. (2021). Composite bridge deck optimization with trajectory-based algorithms. 6th International Conference on Mechanical Models in Structural Engineering, CMMoST 2021, 1-3 December, Valladolid, Spain, pp. 174-187. ISNB: 978-84-09-39323-7

Pincha aquí para descargar

 

Optimización heurística de pórticos de paso de carretera de hormigón armado

A continuación recojo uno de los primeros trabajos que hizo nuestro grupo de investigación en el año 2005 sobre optimización heurística de estructuras de hormigón. Se trata de la optimización mediante varias heurísticas (máximo gradiente, aceptación por umbrales y recocido simulado) de un pórtico de paso de carretera de hormigón armado. En este caso se consideraron 28 variables para definir una solución de pórtico. Este artículo se publicó en la revista Hormigón y Acero. Espero que os sea de interés.

 

Referencia:

CARRERA, J.M.; ALCALÁ, J.; YEPES, V.; GONZÁLEZ-VIDOSA, F. (2005). Optimización heurística de pórticos de paso de carretera de hormigón armado. Hormigón y Acero, 236: 85-95.

Pincha aquí para descargar

Optimización de pasarelas peatonales de sección en cajón y hormigón de alta resistencia

Acaban de publicarnos un artículo en la revista International Journal of Computational Methods and Experimental Measurements un artículo en el que optimizamos pasarelas peatonales de sección en cajón y hormigón de alta resistencia. Se trata de una publicación en abierto, por lo que os dejamos a continuación el artículo completo para su lectura y descarga.

ABSTRACT:

This paper deals with the economic optimization of high-performance post-tensioned concrete box-girder pedestrian bridges. To this end, a program analyzes and evaluates the structural restrictions following Spanish codes for structural concrete and bridge design loads. This problem includes 33 discrete design variables that define the geometry, the concrete, the reinforcing steel bars and the post-tensioned steel. Various acceptance criteria are proposed to modify a variant of the simulated annealing algorithm with a neighborhood move based on the mutation operator from the genetic algorithms (SAMO). An objective methodology based on the extreme value theory is used to determine the number of experimental tests required to provide a solution with user-defined accuracy as compared to a global optimum solution. Results indicate that the local optima found by SAMO2 fits a three parameter Weibull distribution and improves the cost results for this structural problem. The minimum value obtained by SAMO2 differed just 0.34% compared to the theoretical minimum value so that, from the structural engineering perspective, the divergence was small enough to be accepted. High strength concrete performance was further studied in a concrete strength parametric study to acquire more evidence-based knowledge on its implications for economic efficiency. Finally, the study showed that high-strength concrete decreases the cost by 4.5% and the amount of concrete by 26%.

KEYWORDS:

Box-girder bridge, extreme value theory, high-strength concrete, post-tensioned concrete, simulated annealing, Structural optimization

REFERENCE:

YEPES, V.; PÉREZ-LÓPEZ, E.; GARCÍA-SEGURA, T.; ALCALÁ, J. (2019). Optimization of high-performance concrete post-tensioned box-girder pedestrian bridges. International Journal of Computational Methods and Experimental Measurements, 7(2):118-129. DOI: 10.2495/CMEM-V7-N2-118-129

Pincha aquí para descargar

 

 

Optimización de estructuras de hormigón mediante Simulated Annealing

Logo OptimizacionA continuación os dejo un capítulo de un libro de Simulated Annealing, escrito en abierto para su libre difusión, donde explicamos varias aplicaciones del algoritmo de Cristalización Simulada aplicada a estructuras de hormigón armado. En particular: muros ménsula, pórticos de carreteras, marcos de carreteras y pórticos de edificación. Su referencia es:

GONZÁLEZ-VIDOSA-VIDOSA, F.; YEPES, V.; ALCALÁ, J.; CARRERA, M.; PEREA, C.; PAYÁ-ZAFORTEZA, I. (2008) Optimization of Reinforced Concrete Structures by Simulated Annealing. TAN, C.M. (ed): Simulated Annealing. I-Tech Education and Publishing, Vienna, pp. 307-320. (link)

Pincha aquí para descargar

¿Qué es la optimización por cristalización simulada?

La cristalización simulada (también llamado recocido simulado) “Simulated Annealing, SA” constituye una de las estrategias a las que se recurre en la resolución de los problemas de optimización combinatoria. Kirkpatrick, Gelatt y Vecchi la propusieron por primera vez en 1983, y Cerny la propuso de forma independiente en 1985. Estos autores se inspiraron en los trabajos de Metrópolis et al. (1953) sobre Mecánica Estadística. La metaheurística despliega una estructura que se inserta cómodamente en la programación y, además, muestra una considerable habilidad para escapar de los óptimos locales. Fue una técnica que experimentó un auge considerable en la década de los 80 para resolver problemas de optimización mediante modelos matemáticos.

La energía de un sistema termodinámico se compara con la función de coste evaluada para una solución admisible de un problema de optimización combinatoria. En ambos casos se trata de evolucionar de un estado a otro de menor energía o coste. El acceso de un estado metaestable a otro se alcanza introduciendo “ruido” mediante un parámetro de control, denominado temperatura. Su reducción adecuada permite, con una probabilidad elevada, que un sistema termodinámico adquiera un mínimo global de energía. Conceptualmente, es un algoritmo de búsqueda por entornos que selecciona candidatos de forma aleatoria. La alternativa se aprueba si perfecciona la solución actual (D ≤ 0); en caso contrario, será aceptada con una probabilidad e^(-D/T), donde T es el parámetro de temperatura, si D > 0. El proceso se repite cuando la propuesta no es admitida. La selección aleatoria de soluciones degradadas permite eludir los mínimos locales. La cristalización simulada se codifica fácilmente, incluso en problemas complejos y con funciones objetivo arbitrarias. Además, independientemente de la solución inicial, el algoritmo converge estadísticamente a la solución óptima (Lundy y Mees, 1986). En cualquier caso, SA suele ofrecer soluciones valiosas, aunque no informa si ha alcanzado el óptimo absoluto. Por contra, al ser un procedimiento general, en ocasiones no resulta competitivo, aunque sí comparable, frente a otros específicos que aprovechan información adicional del problema. El algoritmo es lento, especialmente si la función objetivo es costosa en términos de tiempo de computación. Además, la cristalización simulada pierde terreno frente a otros métodos más simples y rápidos, como el descenso local, cuando el espacio de las soluciones es poco abrupto o escasean los mínimos locales.

Os dejo un vídeo explicativo:

Referencias

CERNY, V. (1985). Thermodynamical approach to the traveling salesman problem: an efficient simulated algorithm. Journal of Optimization Theory and Applications, 45: 41-51.

KIRKPATRICHK, S.; GELATT, C.D.; VECCHI, M.P. (1983). Optimization by simulated annealing. Science, 220(4598): 671-680.

LUNDY, M.; MEES, A. (1986). Convergence of an Annealing Algorithm. Mathematical programming, 34:111-124.

METROPOLIS, N.; ROSENBLUTH, A.W.; ROSENBLUTH, M.N.; TELLER, A.H.; TELER, E. (1953). Equation of State Calculation by Fast Computing Machines. Journal of Chemical Physics, 21:1087-1092.

GONZÁLEZ-VIDOSA-VIDOSA, F.; YEPES, V.; ALCALÁ, J.; CARRERA, M.; PEREA, C.; PAYÁ-ZAFORTEZA, I. (2008) Optimization of Reinforced Concrete Structures by Simulated Annealing. TAN, C.M. (ed): Simulated Annealing. I-Tech Education and Publishing, Vienna, pp. 307-320. (link)

Diseño heurístico de puentes de hormigón pretensado como ejemplo de docencia de posgrado

Este artículo describe la impartición de un curso de posgrado en el diseño automatizado y optimización económica de estructuras de hormigón. El contenido forma parte de un Máster en Ingeniería de Hormigón que comenzó en octubre de 2007. El curso aplica los algoritmos heurísticos al diseño práctico de estructuras reales de hormigón, tales como muros, pórticos y marcos de pasos inferiores de carreteras, pórticos de edificación, bóvedas, pilas, estribos y tableros de puentes. Se presentan como casos prácticos dos tableros de puente de hormigón pretensado usados en la obra pública de construcción de carreteras. En primer lugar, se aplica SA a un tablero de un puente peatonal de viga artesa de hormigón prefabricado. El  segundo ejemplo aplica TA a un tablero de losa continua de hormigón postesado. Los casos estudiados indican que la optimización heurística es una buena opción para diseñar   estructuras de hormigón pretensado reduciendo los costes.

Pincha aquí para descargar