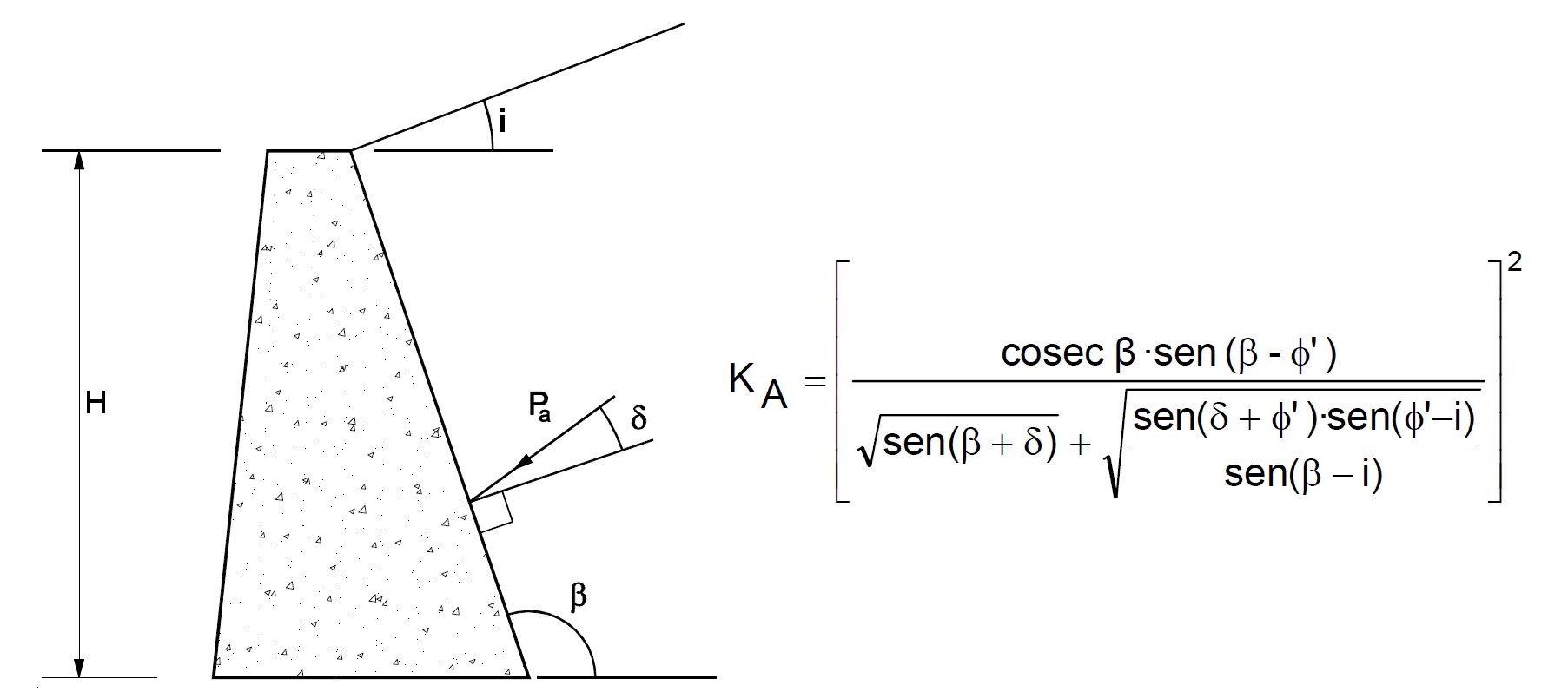
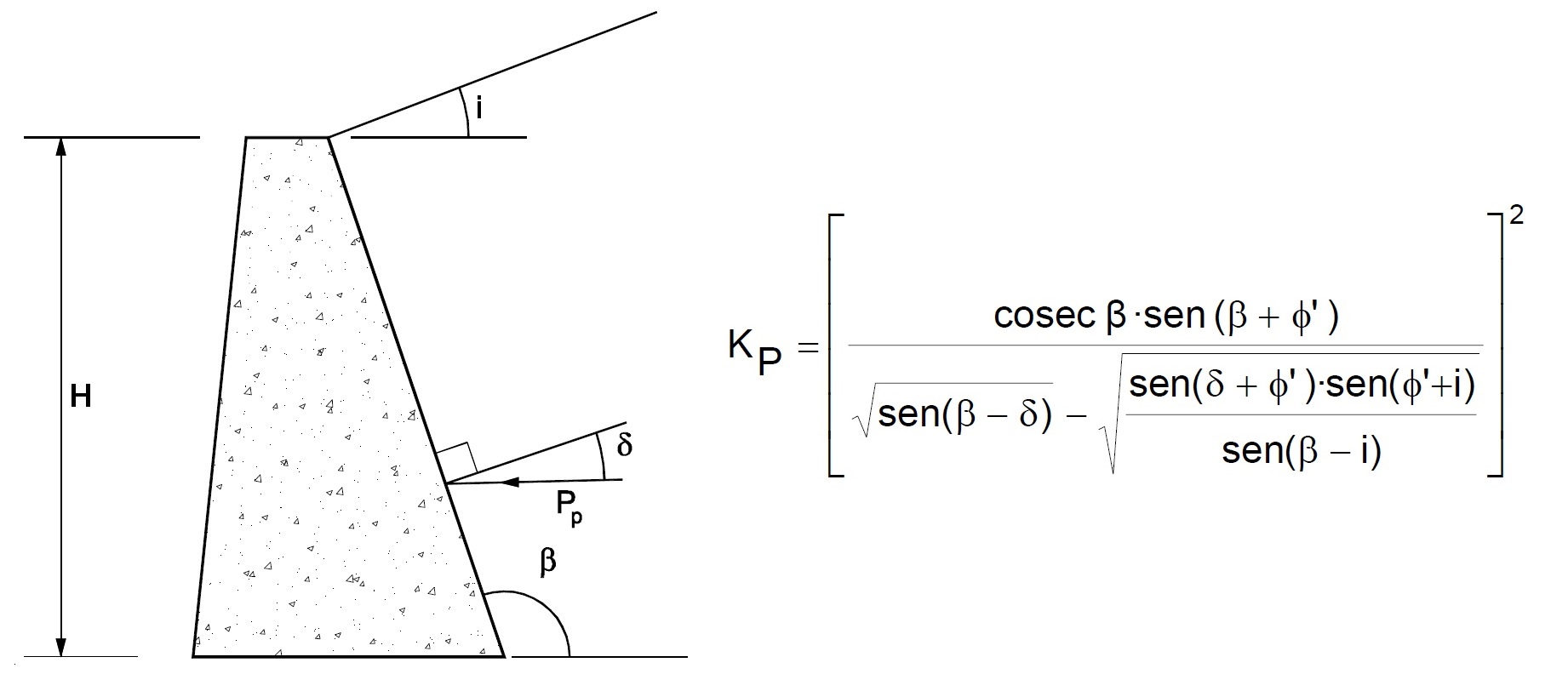
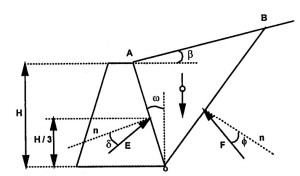
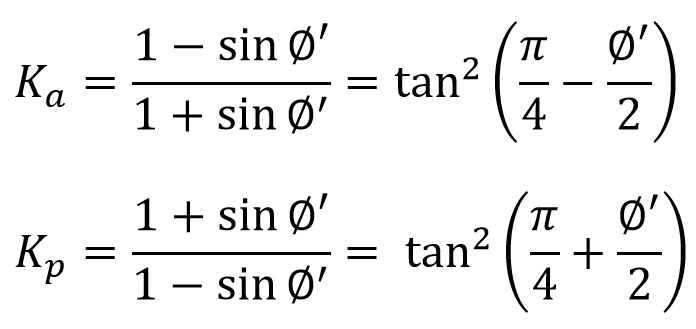muros – El blog de Víctor Yepes

Encofrados de muros

Figura 1. Disposición en obra de un encofrado vertical de muro. Imagen: V. Yepes

Los encofrados de muros se componen por paneles recuperables de encofrado, cuya superficie encofrante generalmente es de madera, y en algunos casos, metálicos. Estos paneles se soportan por bastidores de acero o vigas de madera o acero interconectadas, exigiéndose en muchos casos acabados vistos. Además de los modelos tradicionales, existe la posibilidad de utilizar módulos prefabricados con dimensiones predeterminadas por el fabricante o encofrados a medida.

Así pues, los encofrados de muros se pueden clasificar en tres grandes grupos:

Los construidos en la misma obra a base de un entablado de contrachapado o de tablas, costillas y carreras.
Los prefabricados y montados en obra, consistentes en entablados de contrachapado o de tablas que se unen a elementos de madera.
Los paneles de encofrado prefabricados y patentados, que emplean paramentos de contrachapados unidos y protegidos.

Cuando se trata de muros a dos caras, ya sean circulares o rectos, los esfuerzos del hormigonado a través del panel se transmiten a tirantes internos que atan las dos caras encofrantes. En el caso de muros a una cara, se precisa el respaldo de estructuras metálicas para transferir la carga del encofrado a una cimentación previamente preparada con anclajes perdidos. Estos encofrados verticales presentan agrupaciones de elementos:

El sistema encofrante, que da textura y soporta la presión del hormigón fresco
La estructura de soporte, constituida por un marco exterior y unas costillas interiores de refuerzo

Los encofrados tipo marco operan estructuralmente como un emparrillado plano, apoyándose en los anclajes. En la fase inicial, el encofrado recibe las cargas generadas durante el hormigonado y las distribuye hacia los perfiles que conforman el marco. A su vez, este marco transfiere las cargas desde el forro a los anclajes, especialmente en el caso de los encofrados de doble cara. Los anclajes trabajan principalmente en tracción para sostener el marco.

En los encofrados de una sola cara, los elementos tipo marco transfieren estas cargas hacia una estructura de soporte. En un encofrado de vigas, el forro recibe la presión del hormigón fresco y la distribuye a las vigas, asumiendo la forma de una carga distribuida. Cada viga desempeña la función de una viga continua, con tantos puntos de apoyo como correas tenga el componente. A su vez, cada correa funciona como una viga continua con tantos puntos de apoyo como anclajes estén posicionados sobre él, en el caso de muros encofrados a dos caras, o como estructuras de soporte en el caso de muros encofrados a una cara. Los anclajes soportan las correas, resistiendo todas las cargas transmitidas a través de ellos en forma de tracción.

Figura 2. Encofrado para muros con vigas. Fuente: https://www.peri.es/productos/encofrados/encofrados-para-muros/vario-gt-24-girder-wall-formwork.html#&gid=1&pid=1

Los anclajes se componen de barras de acero de alto límite elástico con rosca autolimpiante. Estos elementos se denominan espadas o espadines. El diámetro más común es Ø15 mm para situaciones habituales. Solo en situaciones de elevadas presiones de hormigón fresco se recurre a diámetros mayores, como Ø20 mm. Las propiedades de las barras de anclaje comerciales están reguladas por la norma DIN 18.216, que establece los coeficientes de seguridad para el cálculo de estas barras (γ_F = 2 para las acciones). Según lo establecido en dicha norma, el valor característico de la tracción máxima admisible es de 90 kN para barras de Ø15 mm y de 150 kN para barras de Ø20 mm.

La transmisión de la carga desde el elemento encofrante hacia la barra, en forma de tracción, se logra a través de una placa de reparto y una tuerca. En muchos casos, los fabricantes integran estos dos componentes en una única pieza.

La barra atraviesa el elemento que será hormigonado, y el conjunto se mantiene en equilibrio debido a que la presión de hormigonado y, por consiguiente, la tracción ejercida sobre la barra, es igual en ambas caras. Para recuperar la barra de anclaje después de que el hormigón ha fraguado, se coloca dentro de un tubo pasamuro que cuenta con conos en ambos extremos, generalmente fabricados en PVC. Suelen tener un diámetro de 22 y 26 mm.

En la actualidad, los elevados costos de mano de obra en la construcción demandan sistemas de encofrado cada vez más simples y eficientes. La mayoría de las empresas optan por sistemas prefabricados de encofrado de uso universal. Estos sistemas permiten la modulación de paneles con pocas piezas diferentes, abordando de manera sencilla, segura y económica las necesidades específicas de la obra. Además, el diseño de los paneles planos facilita un almacenamiento y transporte óptimos.

La resistencia y versatilidad en los paneles modulares hacen de este sistema un producto capaz de abordar con sus elementos estándar la mayoría de situaciones que surgen tanto en edificación como en obra civil. Ya sea para muros de hormigón rectos, circulares, irregulares o para las intersecciones entre estos. Este sistema también permite definir la textura del hormigón al posibilitar la colocación de elementos fácilmente adheribles al panel. De esta manera, se logran texturas de acabado y estética exigidas para el hormigón visto.

En este vídeo vemos el encofrado de un muro a una cara.

Aquí os dejo algunos vídeos más al respecto.

Referencias:

AFECI (2021). Guía sobre encofrados y cimbras. 3ª edición, Asociación de fabricantes de encofrados y cimbras, 76 pp.

YEPES, V. (2024). Estructuras auxiliares en la construcción: Andamios, apeos, entibaciones, encofrados y cimbras. Colección Manual de Referencia, serie Ingeniería Civil. Editorial Universitat Politècnica de València, 408 pp. Ref. 477. ISBN: 978-84-1396-238-2

Cursos:

Curso de estructuras auxiliares en la construcción: andamios, apeos, entibaciones, encofrados y cimbras.

Curso de fabricación y puesta en obra del hormigón.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Nuestra aportación a la 6ª Conferencia Internacional sobre Modelos Mecánicos en Ingeniería Estructural CMMoST 2021

Como suele ser habitual, nuestro grupo de investigación suele presentar algunos de sus trabajos en la Conferencia Internacional sobre Modelos Mecánicos en Ingeniería Estructural. Estamos ya en la sexta edición, la CMMoST 2021, que se va a desarrollar del 1 al 3 de diciembre de 2021 en Valladolid (España). Se trata de un congreso bianual que, como bien indica su blog de presentación, es una excelente oportunidad para presentar a nivel internacional vuestros proyectos y compartir experiencias en el campo de los modelos mecánicos en la ingeniería estructural. CMMoST 2021 va dirigido tanto a investigadores como a profesionales dedicados al desarrollo y aplicación de modelos mecánicos en la ingeniería estructural. De este modo, ingenieros, arquitectos y otros expertos y profesionales relacionados con los modelos estructurales tienen cabida en este congreso internacional.

En esta ocasión, nos presentamos con dos comunicaciones que son parte de la investigación realizada en sendas tesis doctorales en marcha. A continuación os paso el resumen de los dos trabajos. Más adelante os pasaré las comunicaciones completas.

MARTÍNEZ-MUÑOZ, D.; SÁNCHEZ-GARRIDO, A.J.; MARTÍ, J.V.; YEPES, V. (2021). Composite bridge deck optimization with trajectory-based algorithms. 6th International Conference on Mechanical Models in Structural Engineering, CMMoST 2021, 1-3 December, Valladolid, Spain.

ABSTRACT

Bridge optimization can be difficult due to the large number of variables involved in the problem. In this work, the optimization of a steel‐concrete composite box girder bridge has been performed considering cost as objective function. To achieve this objective, Simulated Annealing (SA) has been applied as an example of trajectory‐based algorithm for the optimization of the structure. It is observed that the addition of cells to the bridge cross sections improves not only the section behavior but also the optimization results. Finally, it is observed that the proposed double composite‐action design materializing slabs on the bottom flange on supports, allows eliminating the continuous longitudinal stiffeners. This method automatize the optimization process of an initial design of a composite bridge, which has traditionally been based on the technician’s own experience, allowing to reach results in a more efficient way.

Keywords: Optimization, Structures, Composite bridges, Metaheuristics, Trajectory‐based algorithms.

SÁNCHEZ-GARRIDO, A.J.; MARTÍNEZ-MUÑOZ, D.; NAVARRO, I.J.; YEPES, V. (2021). Neutrosophic logic applied to the multi-criteria evaluation of sustainable alternatives for earth-retaining walls. 6th International Conference on Mechanical Models in Structural Engineering, CMMoST 2021, 1-3 December, Valladolid, Spain.

ABSTRACT

The sustainable design of infrastructures is one of the key aspects for the achievement of the Sustainable Development Goals, given the recognized magnitude of both the economic and environmental impacts of the construction sector. Multi-criteria decision methodologies allow addressing the sustainable design of infrastructures, simultaneously considering the impact of a design on the different dimensions of sustainability. This article proposes the use of neutrosophic logic to solve one of the main problems associated with decision making: the subjectivity of the experts involved. Through the neutrosophic approach of the AHP multi-criteria methodology and the use of the VIKOR technique, the economic and environmental impacts associated with four earth retaining wall designs are analyzed. In the present assessment, the most sustainable response over its life cycle has been found to be the gabion wall.

Keywords: Sustainability, Retaining walls, Neutrosophic logic, AHP, Multi-criteria decision making.

Optimización de muros de contrafuertes mediante algoritmo híbrido de enjambre de partículas y clustering

Acaban de publicarnos un artículo en la revista Mathematics, revista indexada en el primer cuartil del JCR. En este artículo se presenta un algoritmo híbrido de enjambre de partículas y clustering para optimizar el coste y las emisiones de CO $_{2}$ de un muro de contrafuertes. El trabajo se enmarca dentro del proyecto de investigación DIMALIFE que dirijo como investigador principal en la Universitat Politècnica de València.

El diseño de los muros de contrafuertes es un problema de optimización combinatoria de interés debido a las aplicaciones prácticas relativas al ahorro de costos que implica el diseño y la optimización en la cantidad de emisiones de CO $_{2}$ generadas en su construcción. Por otro lado, este problema presenta importantes retos en cuanto a complejidad computacional, pues involucra 32 variables de diseño, por lo que tenemos en el orden de 10^20 combinaciones posibles. En este artículo proponemos un algoritmo híbrido en el que se integra el método de optimización del enjambre de partículas que resuelve los problemas de optimización en espacios continuos con la técnica de clustering db-scan. Este algoritmo optimiza dos funciones objetivo: las emisiones de carbono y el costo económico de los muros de hormigón armado. Para evaluar la contribución del operador del db-scan en el proceso de optimización, se diseñó un operador aleatorio. Se comparan las mejores soluciones, los promedios y los rangos intercuartílicos de las distribuciones obtenidas. A continuación se comparó el algoritmo db-scan con una versión híbrida que utiliza k-means como método de discretización y con una implementación discreta del algoritmo de búsqueda de armonía. Los resultados indican que el operador db-scan mejora significativamente la calidad de las soluciones y que la metaheurística propuesta muestra resultados competitivos con respecto al algoritmo de búsqueda de armonía.

Abstract:

The design of reinforced earth retaining walls is a combinatorial optimization problem of interest due to practical applications regarding the cost savings involved in the design and the optimization in the amount of CO $_{2}$ emissions generated in its construction. On the other hand, this problem presents important challenges in computational complexity since it involves 32 design variables; therefore we have in the order of $10^{20}$ possible combinations. In this article, we propose a hybrid algorithm in which the particle swarm optimization method is integrated that solves optimization problems in continuous spaces with the db-scan clustering technique, with the aim of addressing the combinatorial problem of the design of reinforced earth retaining walls. This algorithm optimizes two objective functions: the carbon emissions embedded and the economic cost of reinforced concrete walls. To assess the contribution of the db-scan operator in the optimization process, a random operator was designed. The best solutions, the averages, and the interquartile ranges of the obtained distributions are compared. The db-scan algorithm was then compared with a hybrid version that uses k-means as the discretization method and with a discrete implementation of the harmony search algorithm. The results indicate that the db-scan operator significantly improves the quality of the solutions and that the proposed metaheuristic shows competitive results with respect to the harmony search algorithm.

Keywords:

CO2 emission; earth-retaining walls; optimization; db-scan; particle swarm optimization

Reference:

GARCÍA, J.; MARTÍ, J.V.; YEPES, V. (2020). The buttressed walls problem: An application of a hybrid clustering particle swarm optimization algorithm. Mathematics, 8(6):862. https://doi.org/10.3390/math8060862

Descargar (PDF, 847KB)

Empuje de tierras, ¿mejor Coulomb o Rankine?

Figura 1. Coulomb y Rankine, autores de dos de los modelos clásicos de empuje de tierras.

El empuje de tierras sobre estructuras de contención ha sido un problema clásico en Geotecnia, pero que es complejo, pues existen numerosas incertidumbres asociadas al comportamiento de los distintos tipos de terreno. Tanto la dificultad en la determinación de las características mecánicas d

el terreno real como la complejidad en las hipótesis de cálculo han llevado a la utilización de simplificaciones útiles en una gran mayoría de casos. Las dos teorías clásicas en la estimación de los empujes del terreno se deben al francés Charles-Agustin de Coulomb (1736-1806) y al escocés William John Macquorn Rankine (1820-1872). Ambos métodos se sustentan en hipótesis diferentes y los resultados que proporcionan no coinciden, salvo en algún caso muy particular.

En cualquier libro de Geotecnia se puede comprobar cómo integrando las ecuaciones diferenciales de las condiciones de equilibrio interno de un elemento diferencial de un terreno horizontal, homogéneo, isótropo y con un comportamiento elástico, la tensión horizontal depende de la vertical. En el caso de que el terreno estuviera confinado lateralmente, con deformación lateral nula, la ley de Hooke proporciona una solución al problema, siendo la relación entre la tensión horizontal y la vertical constante. En cualquier caso, la condición de utilizar una ley de esfuerzo-deformación conveniente constituye el mayor obstáculo para obtener una solución exacta al problema.

Las presiones que soporta un muro o una pantalla reciben el nombre de empujes, que en el caso más general, será la suma del empuje hidrostático más el empuje efectivo ejercido por las partículas del terreno. Se define el coeficiente de empuje como la relación entre la tensión efectiva horizontal y la vertical, y en el caso de que no exista deformación lateral, se denomina coeficiente de empuje al reposo, K₀. De esta forma se podría calcular el empuje sobre un muro que no se deformara lo más mínimo. Sería el caso de un muro de sótano en edificación. Pero los muros no son infinitamente rígidos, se deforman, y dependiendo de si la deformación lateral es negativa (el terreno “se descomprime”) o positiva (el terreno “se comprime”), tendríamos los denominados empujes activos K_a, o pasivos K_p, (K_a<K₀<K_p). Para movilizar el empuje pasivo son necesarios movimientos del muro contra el terreno muy superiores a los necesarios para llegar a una situación de empuje activo. Cuando el empuje pasivo es favorable, debido a la imprecisión en la determinación de su valor real, por seguridad suele despreciarse su efecto o bien se aplica un coeficiente reductor (por ejemplo, de 1,5). Dejamos al lector investigar sobre este asunto en la literatura habitual.

Figura 2. Relación entre empuje del terreno y los movimientos necesarios para su desarrollo (Código Técnico de Edificación)

Lo que nos interesa en esta entrada es conocer las diferencias entre el método de Coulomb y el de Rankine e intentar interpretar cuándo sería mejor utilizar uno u otro método. Las fórmulas se pueden deducir de cualquier libro o manual de geotecnia. En ambos casos se puede generalizar la formulación al caso de terrenos cohesivos, presencia de nivel freático, cargas uniformes sobre el trasdós e inclinación del relleno tras el muro. Siendo σ’_v es la tensión efectiva vertical y c‘ la cohesión efectiva del terreno o relleno del trasdós, el empuje activo P_ase define como la resultante de los empujes unitarios σ’_a que puede determinarse mediante la siguiente fórmula:

y de forma análoga, el empuje pasivo P_p se define como la resultante de los empujes unitarios σ’_p que puede determinarse mediante:

La cohesión es un aspecto favorable para disminuir el empuje del terreno, pero si al final no se acaba desarrollando, nos deja del lado de la inseguridad; por tanto, como a veces es difícil estimar su efecto de forma adecuada, es habitual despreciarla para quedar del lado de la seguridad. Por tanto, se aconseja ser muy cuidadoso a la hora de considerar la cohesión.

Coulomb propuso un modelo para estimar los empujes del terreno planteando el equilibrio de una masa de terreno en forma de cuña al deformarse o moverse el muro. La rotura se produce a lo largo de dos planos, el formado por el interface suelo-muro y el plano de deslizamiento en el terreno. La cuña, formada por los dos planos, se comporta como un bloque rígido. De todas las cuñas posibles, una es la que produce el empuje activo máximo, y ese es el problema resuelto por este ingeniero francés en 1776. El método supone que las superficies de deslizamiento son planas, pero esta hipótesis es muy discutible en el caso del empuje pasivo. El problema queda resuelto para un muro cualquiera, con un trasdós que no necesita ser vertical, y un terreno con una determinada inclinación y con unas cargas sobre su superficie. Se supone conocido el peso específico del terreno, el ángulo de rozamiento interno y el ángulo de rozamiento muro-suelo. Es actualmente el método más empleado para el diseño de muros por métodos de equilibrio límite. Hoy día se emplea con gran efectividad en el cálculo de muros de gravedad, lo que permite considerables ahorros de material. Las fórmulas que siguen indican los coeficientes de empuje activo y pasivo, con las figuras que definen cada uno de los ángulos correspondientes:

El método de Rankine (1857) es más elegante desde el punto de vista matemático, explicando el empuje en términos de rotura por cortante del terreno. Se obtienen los empujes partiendo de un semiespacio infinito que se encuentra en “estado de Rankine“, es decir, un estado de equilibrio plástico y en donde el muro no produce ninguna perturbación. Se supone que el terreno es homogéneo e isótropo y en estado de equilibrio plástico, es decir, se acepta que toda la masa en el trasdós del muro está en situación de rotura y, por tanto, en cualquier punto el estado tensional pertenece a un círculo de Morh que es tangente a la línea de rotura de este suelo; además, como hipótesis adicional, no hay variación de tensiones en los puntos de cualquier plano paralelo a la superficie del semiespacio. Este modelo puede resultar un tanto conservador, pues solo considera el ángulo de rozamiento interno del terreno, olvidando el efecto favorable del rozamiento entre el muro y el terreno. Este método tiene muchas aplicaciones prácticas, por ejemplo, en muros ménsula, donde la suposición de Rankine no supone grandes desventajas y simplifica enormemente los cálculos. El cálculo de empujes sobre un muro con el modelo de Rankine se reduce a obtener las presiones efectivas a la profundidad correspondientes y aplicar las fórmulas correspondientes. De esta forma es muy sencillo calcular terrenos estratificados y considerar la existencia de una carga uniforme en coronación. Además, el método permite estimar si existen grietas de tracción y su profundidad en un terreno que sea cohesivo. Los coeficientes de empuje activo y pasivo para un terreno que forma un ángulo i con la horizontal teniendo en cuenta que la resultante forma un ángulo i con la horizontal, son los siguientes:

Aplicando el teorema de los estados correspondientes de Caquot, se puede generalizar la teoría de Rankine a suelos cohesivos: “Si a un suelo con cohesión que está en situación límite de rotura, simultáneamente le quitamos la cohesión y sumamos a todas las tensiones un término (c’ · cotg Φ’), el suelo sigue estando en la misma situación límite de rotura” (y se le aplican las hipótesis de los suelos sin cohesión).

Figura 3. Círculo de Mohr considerando suelos cohesivos

De las fórmulas deducidas para el empuje activo y pasivo, las fórmulas en ambos modelos coinciden únicamente en el caso de un trasdós vertical del muro, no hay rozamiento suelo-estructura y la superficie del terreno es horizontal. En este caso, los coeficientes de empuje activo y pasivo son los siguientes:

Resumiendo los aspectos básicos expuestos anteriormente, podríamos decir lo siguiente:

En caso de terrenos estratificados, la inclinación del plano de deslizamiento depende de cada terreno, con lo que el problema puede ser indeterminado si utilizamos el modelo de Coulomb. En este caso, Rankine es de más fácil formulación, que suele ser recomendable en el caso de muros ménsula.
El método de Coulomb no tiene en cuenta la presencia de grietas de tracción, por lo que con terrenos cohesivos el cálculo de la profundidad de estas grietas se debe hacer con Rankine.
Si no existe cohesión en el terreno ni adherencia entre muro y terreno, con la teoría de Coulomb se puede determinar que la resultante del empuje activo está situada, desde la base del muro, a un tercio de la altura del muro. Si no es así, entonces el método no proporciona directamente la posición del empuje.
El método de Rankine es difícil de aplicar con geometrías mínimamente complejas (trasdós quebrado, superficies del terreno en el trasdós no planas, cargar arbitrarias sobre éste último) y no es mucho más preciso que el método de Coulomb para estos casos.
El método de Coulomb no estima bien el empuje pasivo, pues la superficie real de rotura no es plana (se asemeja a una espiral logarítmica) y la distribución de empujes difiere bastante de la triangular, proporcionando valores sobredimensionados (del lado de la inseguridad). El método de Rankine es más conservador para el cálculo de empujes pasivos.
El método de Rankine no considera el rozamiento entre el muro y el terreno, lo cual es conservador. Es un aspecto importante en muros de gravedad, cuyos empujes activos se prefieren calcular con Coulomb.
En el método de Coulomb permite la consideración de sobrecargas en el trasdós de cualquier tipo (constante, puntual, triangular, etc.) siempre que sean indefinidas en el sentido longitudinal del muro, pues basta introducirlas en las ecuaciones de equilibrio. Con Rankine es sencillo si se trata de una sobrecarga constante.

REFERENCIAS:

GARCÍA VALCARCE, A. (dir.) (2003). Manual de edificación: mecánica de los terrenos y cimientos. CIE Inversiones Editoriales Dossat-2000 S.L. Madrid, 716 pp.
GONZÁLEZ CABALLERO, M. (2001). El terreno. Edicions UPC, Barcelona, 309 pp.
IZQUIERDO, F.A. (2001). Cuestiones de geotecnia y cimientos. Editorial Universidad Politécnica de Valencia, 227 pp.
LAMBE, T.W.; WHITMAN, R.V. (1996). Mecánica de suelos. Limusa, México, D.F., 582 pp.
MINISTERIO DE FOMENTO (2002). Guía de Cimentaciones. Dirección General de Carreteras.
MINISTERIO DE LA VIVIENDA (2006). Código Técnico de la Edificación
YEPES, V. (2020). Procedimientos de construcción de cimentaciones y estructuras de contención. Colección Manual de Referencia, 2ª edición. Editorial Universitat Politècnica de València, 480 pp. Ref. 328. ISBN: 978-84-9048-903-1.
YEPES, V. (2023). Maquinaria y procedimientos de construcción. Problemas resueltos. Colección Académica. Editorial Universitat Politècnica de València, 562 pp. Ref. 376. ISBN 978-84-1396-174-3

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Curso en línea de “Procedimientos de Construcción de cimentaciones y estructuras de contención en obra civil y edificación”

La Universitat Politècnica de València, en colaboración con la empresa Ingeoexpert, ha elaborado un Curso online sobre “Procedimientos de Construcción de cimentaciones y estructuras de contención en obra civil y edificación”. El curso, totalmente en línea, se desarrollará en 6 semanas, con un contenido de 50 horas de dedicación del estudiante. Empieza el 9 de septiembre de 2019 y termina el 21 de octubre de 2019. Hay plazas limitadas.

Toda la información la puedes encontrar en esta página: https://ingeoexpert.com/cursos/curso-de-procedimientos-de-construccion-de-cimentaciones-y-estructuras-de-contencion-en-obra-civil-y-edificacion/?v=04c19fa1e772

Os paso un vídeo explicativo y os doy algo de información tras el vídeo.

Este es un curso básico de construcción, cimentaciones y estructuras de contención en obras civiles y de edificación. Se trata de un curso que no requiere conocimientos previos especiales y está diseñado para que sea útil a un amplio abanico de profesionales con o sin experiencia, estudiantes de cualquier rama de la construcción, ya sea universitaria o de formación profesional. Además, el aprendizaje se ha escalonado de modo que el estudiante puede profundizar en aquellos aspectos que más les sea de interés mediante documentación complementaria y enlaces de internet a vídeos, catálogos, etc.

En este curso aprenderás las distintas tipologías y aplicabilidad de los cimientos y las estructuras de contención utilizados en obras de ingeniería civil y de edificación. El curso índice especialmente en la comprensión de los procedimientos constructivos y la maquinaria específica necesaria para la ejecución de los distintos tipos de cimentación (zapatas, losas de cimentación, pilotes, micropilotes, cajones, etc.) así como los distintos tipos de estructuras de contención (muros pantalla, pantallas de pilotes y micropilotes, tablestacas, entibaciones, muros, etc.). Es un curso de espectro amplio que incide especialmente en el conocimiento de la maquinaria y procesos constructivos, y por tanto, resulta de especial interés desarrollar el pensamiento crítico del estudiante en relación con la selección de las mejores soluciones constructivas para un problema determinado. El curso trata llenar el hueco que deja la bibliografía habitual donde los aspectos de proyecto, geotecnia, estructuras de hormigón, etc., oscurecen los aspectos puramente constructivos. Además, está diseñado para que el estudiante pueda ampliar por sí mismo la profundidad de los conocimientos adquiridos en función de su experiencia previa o sus objetivos personales o de empresa.

El contenido del curso está organizado en 20 unidades didácticas, que constituyen cada una de ellas una secuencia de aprendizaje completa. La dedicación aproximada para cada unidad se estima en 2-3 horas, en función del interés del estudiante para ampliar los temas con el material adicional. Además, al finalizar cada unidad didáctica, el estudiante afronta una batería de preguntas cuyo objetivo fundamental es afianzar los conceptos básicos y provocar la duda o el interés por aspectos determinados del tema abordado. Al final se han diseñado cuatro unidades didácticas adicionales cuyo objetivo fundamental consiste en afianzar los conocimientos adquiridos a través del desarrollo de casos prácticos, donde lo importante es desarrollar el espíritu crítico y la argumentación a la hora de decidir la conveniencia de un procedimiento constructivo. Por último, al finalizar el curso se realiza una batería de preguntas tipo test cuyo objetivo es conocer el aprovechamiento del curso, además de servir como herramienta de aprendizaje.

El curso está programado para una dedicación de 50 horas de dedicación por parte del estudiante. Se pretende un ritmo moderado, con una dedicación semanal de 6 a 10 horas, dependiendo de la profundidad de aprendizaje requerida por el estudiante, con una duración total de 6 semanas de aprendizaje.

Objetivos

Al finalizar el curso, los objetivos de aprendizaje básicos son los siguientes:

Comprender la utilidad y las limitaciones de las cimentaciones y estructuras de contenciónempleadas en la construcción de obras civiles y de edificación
Evaluar y seleccionar el mejor tipo de cimentación y estructura de contención necesario para una construcción en unas condiciones determinadas, considerando la economía, la seguridad y los aspectos medioambientales

Programa

– Unidad 1. Concepto y clasificación de cimentaciones
– Unidad 2. Cimentaciones superficiales. Parte 1
– Unidad 3. Cimentaciones superficiales. Parte 2
– Unidad 4. Cimentaciones por pozos y cajones
– Unidad 5. Conceptos fundamentales y clasificación de pilotes
– Unidad 6. Pilotes de desplazamiento prefabricados
– Unidad 7. Pilotes de desplazamiento hormigonados “in situ”
– Unidad 8. Pilotes perforados hormigonados “in situ”. Parte 1
– Unidad 9. Pilotes perforados hormigonados “in situ”. Parte 2
– Unidad 10. Equipos para la perforación de pilotes
– Unidad 11. Estructuras de contención de tierras. Muros
– Unidad 12. Pantallas de hormigón
– Unidad 13. Estabilidad de las excavaciones. Entibaciones.
– Unidad 14. Tablestacas y anclajes
– Unidad 15. Hinca de pilotes y tablestacas
– Unidad 16. Descabezado de pilotes y muros pantalla
– Unidad 17. Caso práctico 1
– Unidad 18. Caso práctico 2
– Unidad 19. Caso práctico 3 d
– Unidad 20. Cuestionario final del curso

Profesorado

Víctor Yepes Piqueras

Ingeniero de Caminos, Canales y Puertos (1982-1988). Número 1 de promoción (Sobresaliente Matrícula de Honor). Especialista Universitario en Gestión y Control de la Calidad (2000). Doctor Ingeniero de Caminos, Canales y Puertos, Sobresaliente “cum laude”. Catedrático de Universidad en el área de ingeniería de la construcción en la Universitat Politècnica de València y profesor, entre otras, de las asignaturas de Procedimientos de Construcción en los grados de ingeniería civil y de obras públicas. Su experiencia profesional se ha desarrollado fundamentalmente en Dragados y Construcciones S.A. (1989-1992) como jefe de obra y en la Generalitat Valenciana como Director de Área de Infraestructuras e I+D+i (1992-2008). Ha sido Director Académico del Máster Universitario en Ingeniería del Hormigón (2008-2017), obteniendo durante su dirección la acreditación EUR-ACE para el título. Profesor Visitante en la Pontificia Universidad Católica de Chile. Investigador Principal en 5 proyectos de investigación competitivos. Ha publicado más de un centenar de artículos en revistas indexadas en el JCR. Autor de 8 libros, 22 apuntes docentes y más de 250 comunicaciones a congresos. Ha dirigido 14 tesis doctorales, con 4 más en marcha. Sus líneas de investigación actuales son las siguientes: (1) optimización sostenible multiobjetivo y análisis del ciclo de vida de estructuras de hormigón, (2) toma de decisiones y evaluación multicriterio de la sostenibilidad social de las infraestructuras y (3) innovación y competitividad de empresas constructoras en sus procesos. Tiene experiencia contrastada en cursos a distancia, destacando el curso MOOC denominado “Introducción a los encofrados y las cimbras en obra civil y edificación”, curso que ya ha tenido cuatro ediciones con más de 17000 estudiantes inscritos.

Referencia:

YEPES, V. (2020). Procedimientos de construcción de cimentaciones y estructuras de contención. Colección Manual de Referencia, 2ª edición. Editorial Universitat Politècnica de València, 480 pp. Ref. 328. ISBN: 978-84-9048-903-1.

Muro de fábrica

Figura 1. Muro de mampostería. Fuente: http://www.generadordeprecios.info/

Los muros de fábrica están constituidos por piedras naturales, ladrillos o bloques de hormigón, que se construyen de forma manual.

Se denominan muros de sillería aquellos formados por piedras labradas finamente, de forma que las piedras se sostienen mutuamente por yuxtaposición, asentándose sobre otras mediante mortero.

Los muros de mampostería están formados por piedras sin labrar o labradas toscamente, que se colocan en dos paramentos, realizándose posteriormente su relleno (Figuras 1 y 2). La forma en la que se disponen las piezas se denomina aparejo. Los mampuestos pueden unirse mediante una argamasa o mortero o bien sin ella, en los llamados muros secos.

Figura 2. Arquitectura popular. Muro de mampostería de granito, La Torre (Ávila). Fuente: https://commons.wikimedia.org/wiki/File:Mamposter%C3%ADa_1.JPG

Os dejo a continuación un vídeo corto sobre cómo se construye un muro de piedra.

Aquí os dejo cómo se hace un muro de piedra en Los Pedroches. Destaca este oficio que se pierde en el tiempo.

Hay intentos de industrialización de este tipo de muros, pero no acaban de generalizarse. Os dejo un artículo al respecto, pero en este caso, restringido a la técnica del tapial.

Descargar (PDF, 2.44MB)

Referencias:

VON MAG, A.; RAUCH, M. (2011). Paredes de tapial y su industrialización (encofrados y sistemas de compactación). Informes de la Construcción, 63:523, 35-40.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Muros de gaviones flexibles

Gaviones flexibles. Fuente: http://gavionesflexibles.com/

Los muros de gaviones propiamente dichos consisten en un recipiente de forma prismática rectangular, relleno de material granular de distintos tamaños, de enrejado metálico de malla hexagonal, que puede ser de triple torsión o electrosoldada dependiendo de las características de la obra.

Sin embargo, se pueden fabricar muros flexibles utilizando la misma idea pero con otros materiales. Son los llamados muros de gaviones flexibles. Consisten en unas celdas realizadas con materiales geosintéticos, que permiten su relleno con tierras u otros materiales como mezclas de grava-cemento, de tierras con cal, etc. Se obtiene de esta forma un muro de tierra sostenida, que funciona por gravedad. Además, constituyen barreras de contención muy flexibles que pueden resultar de gran interés en actuaciones de emergencia como ante desbordamiento de ríos. También pueden ser de gran interés como complemento de obras civiles o ambientales.

Os dejo unos vídeos de la empresa Contflexdique gaviones flexibles donde se puede ver cómo se monta un muro flexible de estas características. Espero que os gusten:

Referencia:

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Muros de gaviones

Los gaviones consisten en un recipiente de forma prismática rectangular, relleno de material granular de distintos tamaños, de enrejado metálico de malla hexagonal, que puede ser de triple torsión o electrosoldada dependiendo de las características de la obra. Estas estructuras, con forma cilíndrica, se utilizaron por primera vez en 1893 por la empresa Maccaferri para el cerramiento de la rotura de un embalse en el río Reno, en la ciudad de Bolonia.

Son muros que presentan una elevada resistencia, puesto que al ser totalmente permeables alivian las tensiones que se acumulan en el trasdós de los muros tradicionales. Asimismo debido a su gran flexibilidad, soportan movimientos y asientos diferenciales sin pérdida de eficiencia. Además, son muros que se construyen de forma sencilla y económica. Sin embargo, hay que tener presente que las mallas de acero galvanizado se corroen en ambientes ácidos, por lo que la falta de control de calidad en los amarres de la malla pueden provocar problemas.

Sin embargo, tal y como podemos ver en la siguiente fotografía del blog de Pablo Nieto, resulta imprescindible evitar el lavado del terreno sobre el que asienta para evitar descalzarlos. Para ello se debería proteger el intradós con un geotextil.

Actividad propuesta:

Tras el visionado de los vídeos que podéis ver a continuación, estaréis en condiciones de responder de forma razonada a las siguientes preguntas:

¿Cómo se ejecuta un muro de gaviones? Describe y secuencia las fases constructivas.
¿Necesitan mechinales los muros de gaviones?
¿Cómo se hace la excavación necesaria para realizar el muro de gavión?
¿Se pueden utilizar los muros de gaviones en terrenos blandos e inestables, que presenten asentamientos apreciables? Justifica la respuesta.
¿Qué diferencias existen entre los diques de gaviones y los de mampostería cuando se utilizan como obras de diques de retención en la cuenca de un barranco?

Referencia:

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Laboratorio virtual: empuje de tierras sobre un muro según Coulomb

El ingeniero militar francés Charles-Augustin de Coulomb (1776) fue el primero en estudiar el problema de las presiones laterales del terreno y estructuras de retención. Este autor introduce una simplificación importante para calcular el empuje: se limitó a usar la teoría de equilibrio que considera que una cuña de terreno en rotura imitada por el trasdós y por un plano que pasa por el pie del muro como un cuerpo en movimiento para determinar la presión lateral limitante. La presión limitante horizontal en fallo en extensión o compresión se determinan a partir de K_a y K_p respectivamente. Se supone que la superficie de deslizamiento es plana, el drenaje del muro funciona bien y que no hay presiones intersticiales en el terreno. Aunque con simplificaciones, esta teoría permite calcular problemas en los cuales el paramento no es vertical y la superficie de relleno tiene cualquier forma.

$K_a = frac{ cos ^2 left( phi - theta right)}{cos ^2 theta cos left( delta + theta right) left( 1 + sqrt{ frac{ sin left( delta + phi right) sin left( phi - beta right)}{cos left( delta + theta right) cos left( beta - theta right)}} right) ^2}$

$K_p = frac{ cos ^2 left( phi + theta right)}{cos ^2 theta cos left( delta - theta right) left( 1 - sqrt{ frac{ sin left( delta + phi right) sin left( phi + beta right)}{cos left( delta - theta right) cos left( beta - theta right)}} right) ^2}$

Para que se pueda estudiar de forma cualitativa el efecto del empuje, se aporta un Laboratorio Virtual. El objetivo de este objeto de aprendizaje consiste en entender cómo varía el empuje activo horizontal sobre un muro aplicando la teoría de Coulomb. Éste coeficiente varía en función del ángulo de rozamiento interno del terreno, del ángulo de rozamiento de terreno y muro, y de la inclinación del muro. Supondremos un relleno horizontal sobre el muro.

Enlace al laboratorio virtual: https://laboratoriosvirtuales.upv.es/eslabon/EmpujeHorizontal/

Referencias:

Coulomb C.A., (1776). Essai sur une application des regles des maximis et minimis a quelques problemes de statique relatifs a l’architecture. Memoires de l’Academie Royale pres Divers Savants, Vol. 7

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

¿Cómo predimensionar un muro sin calculadora?

Fuerzas actuantes sobre muro de contención

Los muros de contención de tierras constituyen una de las estructuras más frecuentes en la construcción de obras civiles y de edificación, siendo habitual la tipología de muros ménsula de hormigón armado. El proyecto de estos elementos de contención constituye un problema de interacción entre el suelo y la estructura cuya finalidad consiste en retener un material de forma suficientemente segura y económica.

Los muros se proyectan basándose en la validación de un diseño inicial que se modifica sucesivamente hasta cumplir con todas las exigencias. En primer lugar, se adopta una geometría previa empleando reglas de predimensionamiento sancionadas por la práctica o referencias de casos similares. Sobre este diseño tentativo se analiza el cumplimiento de determinados requisitos de seguridad (estabilidad y resistencia) y durabilidad. Si la estructura no cumple estos requerimientos, o si lo hace de forma muy holgada, se modifica el esquema inicial y se repite el proceso.

Diseño estructural por el método de prueba y error

Todo ello conforma un panorama de procedimientos artesanales de diseño alejados de una metodología objetiva en la elección de las dimensiones y los materiales. Tales métodos conducen a proyectos seguros estructuralmente, pero cuya economía queda muy ligada a la experiencia previa del ingeniero. Con todo, una estructura no sólo debe cumplir las condiciones de seguridad, calidad y funcionalidad, sino que además debe construirse al menor coste posible.

Algunos trabajos sobre optimización han tratado de resolver el diseño automatizado de estos problemas y buscar soluciones óptimas desde el punto de vista económico y medioambiental. Para aquellos que quieran profundizar en el tema, podéis consultar las referencias.

Pero, para los que queráis predimensionar rápidamente, os paso una serie de reglas prácticas que creo son de interés y que permiten realizar presupuestos y encajes rápidos para este tipo de estructuras, siempre dentro de rangos habituales o normales (entre 4 y 10 m). Llamamos altura total la distancia entre la parte inferior de la zapata y la parte superior del alzado.

“La zapata de un muro tendrá una longitud igual a las dos terceras partes de su altura total. El canto de la zapata y el espesor del alzado serán la décima parte de la altura total. La longitud del talón será la quinta parte de la altura total más 1 metro”.

“El volumen de hormigón necesario será la sexta parte del cuadrado de la altura total, repartido en proporción 3 a 2 entre el alzado y la zapata. Además, se precisan en torno a 60 kg de acero por cada metro cúbico de hormigón”.

Para los que queráis ser más precisos, os dejo una pequeña calculadora gráfica que permite obtener dicho predimensionamiento. Basta que apretéis al botón “DIBUJAR”. Esta página se encuentra en https://laboratoriosvirtuales.upv.es/eslabon/Ejercicio?do=PredimensionamientoMuros

Referencia:

YEPES, V.; ALCALÁ, J.; PEREA, C.; GONZÁLEZ-VIDOSA, F. (2008). A Parametric Study of Optimum Earth Retaining Walls by Simulated Annealing. Engineering Structures, 30(3): 821-830. ISSN: 0141-0296.

YEPES, V.; GONZÁLEZ-VIDOSA, F.; ALCALÁ, J.; VILLALBA, P. (2012). CO₂-Optimization Design of Reinforced Concrete Retaining Walls based on a VNS-Threshold Acceptance Strategy. Journal of Computing in Civil Engineering ASCE, 26 (3):378-386. DOI: 10.1061/(ASCE)CP.1943-5487.0000140.