Acaban de publicarnos un artículo en la revista Structure and Infrastructure Engineering (revista indexada en el JCR) sobre la aplicación de la lógica neutrosófica (una generalización de la lógica difusa y la lógica intuicionista) al diseño y mantenimiento de puentes en ambiente marino. El trabajo se enmarca dentro del proyecto de investigación DIMALIFE que dirijo como investigador principal en la Universitat Politècnica de València.
Acaban de publicarnos un artículo en la revista Structure and Infrastructure Engineering (revista indexada en el JCR) sobre la aplicación de la lógica neutrosófica (una generalización de la lógica difusa y la lógica intuicionista) al diseño y mantenimiento de puentes en ambiente marino. El trabajo se enmarca dentro del proyecto de investigación DIMALIFE que dirijo como investigador principal en la Universitat Politècnica de València.
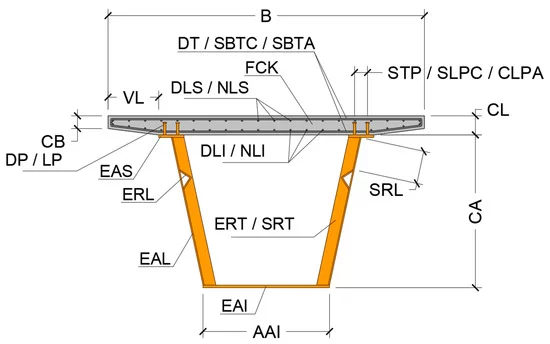
La metodología propuesta utiliza la lógica neutrosófica para obtener los pesos en un Proceso Analítico Jerárquico (AHP) que considerar la subjetividad de los expertos en el proceso de toma de decisión. Se ha aplicado al diseño sostenible de puentes y su mantenimiento considerando simultáneamente las tres dimensiones de la sostenibilidad.
El artículo se puede descargar gratuitamente en el siguiente enlace:
https://www.tandfonline.com/eprint/2KZDAHNK4BPJKPSY4XSF/full?target=10.1080/15732479.2019.1676791
ABSTRACT:
Essential infrastructures such as bridges are designed to provide a long-lasting and intergenerational functionality. In those cases, sustainability becomes of paramount importance when the infrastructure is exposed to aggressive environments, which can jeopardise their durability and lead to significant maintenance demands. The assessment of sustainability is however often complex and uncertain. The present study assesses the sustainability performance of 16 alternative designs of a concrete bridge deck in a coastal environment on the basis of a neutrosophic group analytic hierarchy process (AHP). The use of neutrosophic logic in the field of multi-criteria decision-making, as a generalisation of the widely used fuzzy logic, allows for a proper capture of the vagueness and uncertainties of the judgements emitted by the decision-makers. TOPSIS technique is then used to aggregate the different sustainability criteria. From the results, it is derived that only the simultaneous consideration of the economic, environmental and social life cycle impacts of a design shall lead to adequate sustainable designs. Choices made based on the optimality of a design in only some of the sustainability pillars will lead to erroneous conclusions. The use of concrete with silica fume has resulted in a sustainability performance of 46.3% better than conventional concrete designs.