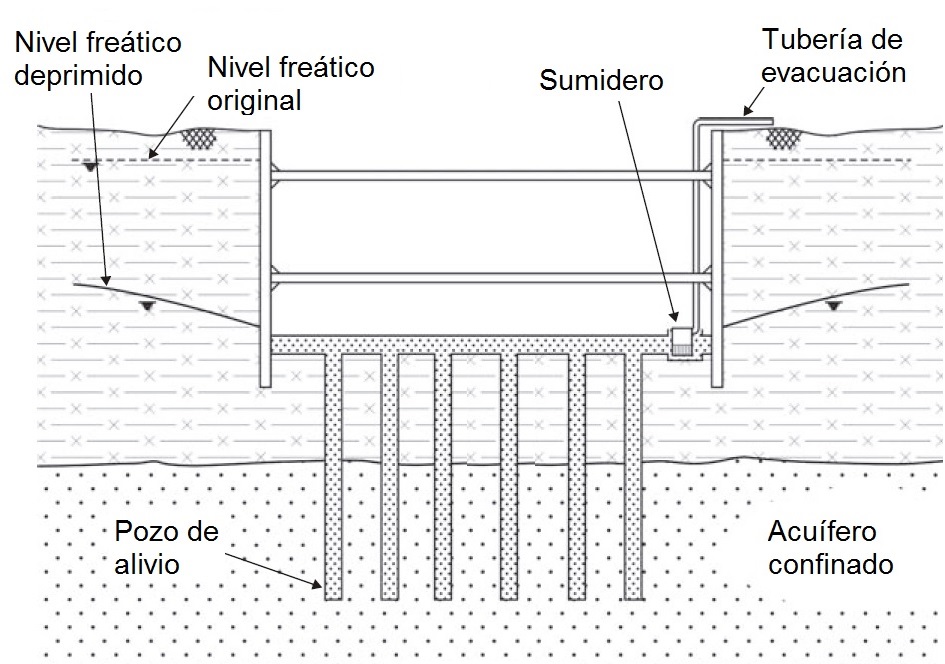
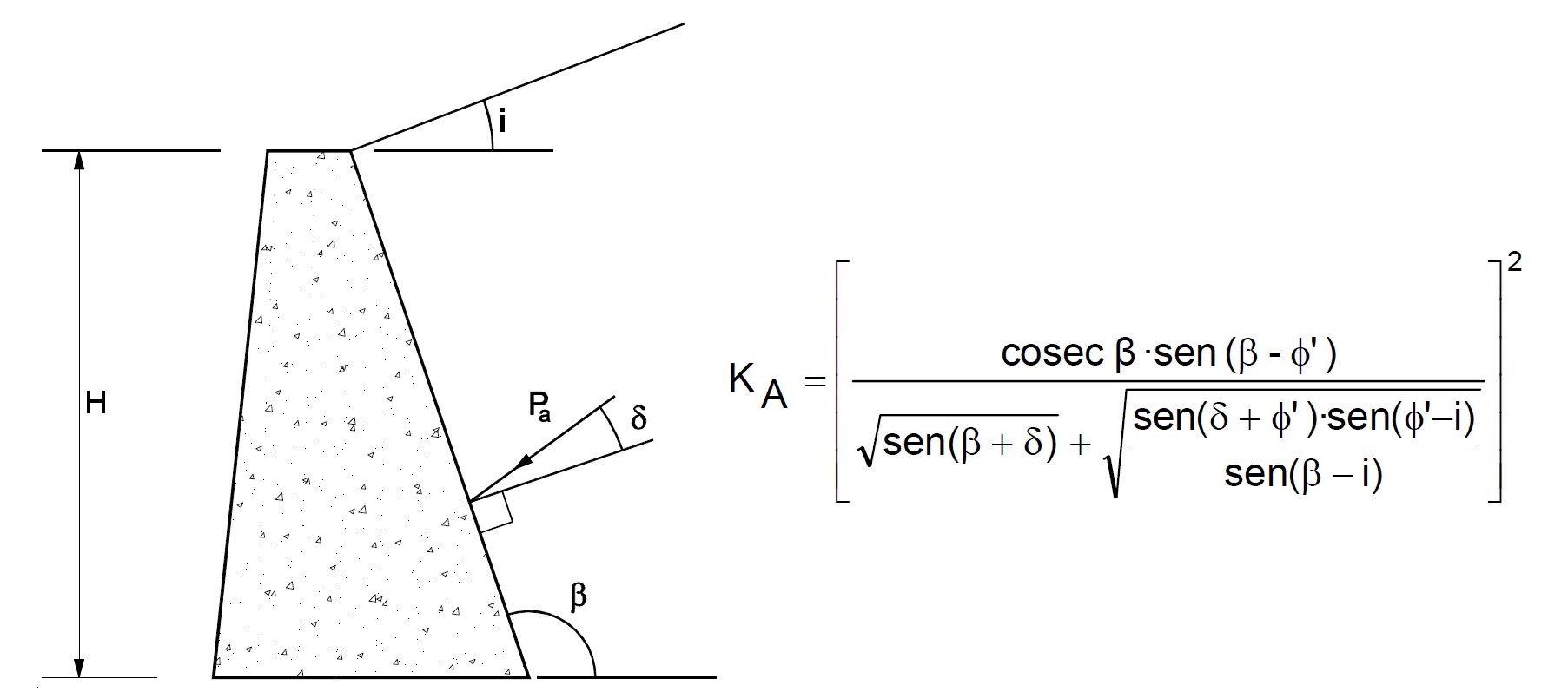
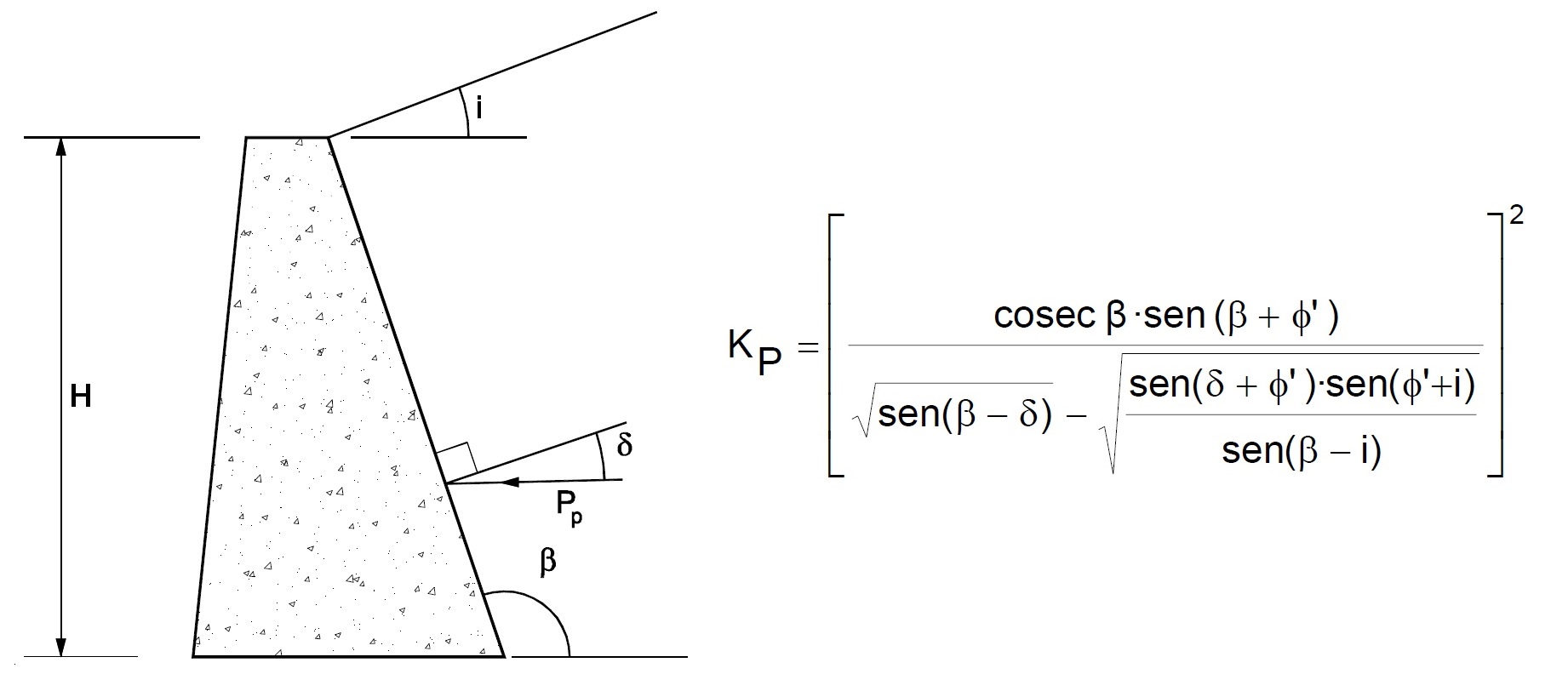
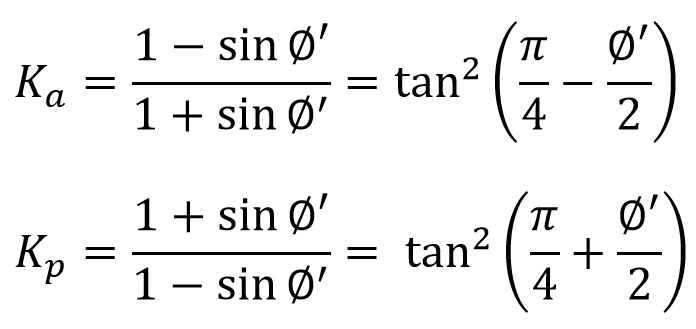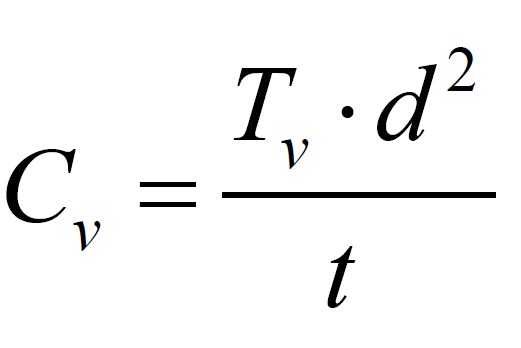geotecnia – Página 2 – El blog de Víctor Yepes

Prólogo y reflexiones sobre la docencia de la asignatura de Procedimientos de Construcción

Estoy en este momento revisando la última prueba de imprenta de un Manual de Referencia (revisado por el sistema doble ciego) de la Universitat Politècnica de València, del cual soy autor. Se trata de un libro de 422 páginas, 259 ilustraciones y 325 preguntas de autoevaluación que se denomina “Procedimientos de construcción para la compactación y mejora del terreno”. Su referencia es el número 428 y os pasaré el enlace para que lo podáis conseguir en cuanto se publique.

Sin embargo, no me he podido resistir a adelantar el prólogo que he escrito a este libro y que, además de presentarlo, sirve como reflexión a la docencia de la asignatura “Procedimientos de Construcción” que actualmente se imparte en los grados de ingeniería civil y de ingeniería de obras públicas de la Escuela Técnica Superior de Ingeniería de Caminos, Canales y Puertos de Valencia.

Prólogo

La docencia de una asignatura como “Procedimientos de Construcción” resulta complicada debido a que se debe enseñar al futuro ingeniero civil cómo hacer las obras. Eso incluye no solo las fases constructivas, sino también aspectos de gran relevancia como es el conocimiento de la maquinaria y los medios auxiliares, la seguridad y salud, el impacto ambiental de las obras y, sobre todo, el conocimiento básico necesario en geotecnia, resistencia de materiales, mecánica, cálculo de estructuras, gestión de empresas, planificación de obras y economía. Todo ello para acertar en la selección del mejor proceso constructivo para una obra determinada. Y todo este conocimiento debe abordarse con una experiencia nula o muy pequeña del alumnado en relación con la realidad física de las obras.

La pregunta es inmediata: ¿Cómo podemos llevar la obra al estudiante en un aula? Resulta evidente la necesidad de que los futuros profesionales pisen las obras lo máximo posible y realicen prácticas en empresa. Pero esta experiencia no es suficiente para adquirir las competencias y conocimientos necesarios.

El problema crece cuando este tipo de asignaturas de construcción se imparten en los primeros cursos de los grados. En los planes antiguos, “Procedimientos Generales de Construcción y Organización de Obras” se impartía en los últimos cursos, incluso en paralelo con la asignatura de Proyectos. Ello permitía al estudiante aplicar todos los conocimientos adquiridos con anterioridad y hacía que la asignatura se pudiese entender con mayor profundidad.

Pero el problema sigue siendo el mismo. Me acuerdo que esta asignatura la estudié en cuarto curso de la titulación de ingeniero de caminos, canales y puertos, cuando el plan se desarrollaba en seis cursos. En aquella época, hablo del año 1986, D. Hermelando Corbí Abad, profesor de la asignatura, utilizaba todos los medios disponibles en su momento como el proyector de opacos, fotografías que nos pasábamos de mano en mano o catálogos de máquinas o de empresas para que nos imagináramos cómo se podría hacer una obra. Y, sobre todo, pizarra, mucha pizarra. Tomábamos apuntes en clase y teníamos fotocopias mecanografiadas por el profesor que nos servían a modo de texto. Todo se complementaba con abundantes visitas a obras y excursiones organizadas que nos abrían los ojos, el compañerismo y la ilusión por esta apasionante profesión.

Cuando en el año 1994 empecé a impartir por primera vez la asignatura, tuve que recurrir a todo tipo de estrategias disponibles en aquel momento. Era entonces profesor asociado, más joven, pero con años ya de experiencia en el sector público y privado. Usábamos vídeos en VHS, transparencias que nos permitían ahorrar mucha pizarra, fotografías y catálogos. Se completaba con las visitas a obra. Pero el problema de acercar la realidad al estudiante seguía siendo complicado. Además, las técnicas constructivas, y sobre todo las máquinas y los elementos auxiliares, cambiaban de forma acelerada. Todo demasiado rápido para los medios de los que disponíamos.

Sin embargo, la aparición de los ordenadores, el PowerPoint y, sobre todo, internet, revolucionó todo con el cambio de milenio. Nada volvió a ser como antes. La información y las novedades se acumularon en mi ordenador. Cientos de fotografías, vídeos y documentación se perdía entre las carpetas de mi disco duro. Había que poner orden.

El descubrimiento de las ventajas que tenía disponer de una bitácora digital fue algo que revolucionó mi forma de impartir las clases de esta asignatura. En efecto, el 5 de marzo de 2012 empecé el que iba a ser un blog personal para organizar la información que tenía dispersa en mi ordenador. Fue una auténtica revolución. Podía ordenar por entradas información dispersa sobre temas de construcción, incluyendo fotografías, vídeos y enlaces a otros documentos. Nada volvería a ser lo mismo. Los estudiantes disponían de una herramienta con la que tener toda la información, no solo de clase, sino que esta la podían ampliar hasta donde quisieran buceando en internet. Así nació el “Blog de Víctor Yepes” https://victoryepes.blogs.upv.es/, que hoy tiene casi 1 500 artículos y más de 5 000 visitas diarias. Además, con la potencia de las redes sociales, toda la información se multiplicaba de forma exponencial.

El paso siguiente era el lógico y normal. Se trataba de depurar y mejorar la información para hacer un libro. Así surgieron una serie de textos docentes que, bajo el nombre de Manual de Referencia, edita la Universitat Politècnica de València. Además, este libro en particular, sirve de base para un curso en línea, gratuito y masivo que, bajo el mismo nombre, se imparte desde este mismo año en la plataforma edX, donde colabora nuestra universidad. En el enlace https://www.edx.org/course/introduccion-procedimientos-construccion-obra-civil se puede acceder al curso en cualquier momento, con la posibilidad de obtener un certificado oficial de dicho curso.

En cuanto a la estructura de este libro, realmente tiene dos grandes partes, una dedicada a la compactación mecánica de los suelos y, la segunda, que se centra en las técnicas de mejora del terreno. Si bien es cierto que la compactación mecánica no deja de ser una técnica de mejora del terreno, por su importancia y generalidad en las obras, se ha tratado como una parte diferenciada. También podréis encontrar un buen número de referencias y una cantidad nada desdeñable de preguntas tipo test con sus respuestas para averiguar si habéis comprendido bien lo explicado en el texto. Al final podréis localizar un índice temático que, de buen seguro, servirá para encontrar información de forma rápida.

La necesidad de un libro como este surge para rellenar un hueco editorial importante. Si bien se pueden encontrar cientos de libros de gran calidad en materias tales como la geotecnia y la mecánica de suelos, la resistencia de materiales y cálculo de estructuras, la hidráulica, etc., son pocos los que se dedican a desgranar los procedimientos constructivos, la maquinaria y los medios auxiliares necesarios para ello.

El reto fue bastante importante. Se trató de estructurar información muy dispersa, técnicas clásicas con otras de rabiosa actualidad, maquinaria que, año tras año, deja a los modelos anteriores obsoletos. Y, afortunadamente, es posible que, en unos años, parte de las técnicas contenidas en este volumen queden como recuerdos del pasado, dando paso a la robotización, la inteligencia artificial, los gemelos digitales y otras muchas técnicas emergentes que van a desdibujar la forma que tenemos de entender las obras.

Por último, y aunque se ha realizado un esfuerzo minucioso por revisar el manuscrito, es posible que pueda existir alguna errata típica de una obra que se edita por vez primera. Asumo la responsabilidad de cualquier error y, en la medida de lo posible, trataré de subsanar y mejorar los aspectos o sugerencias que me hagáis llegar.

Este libro, a partir de ahora, deja de ser mío y pasa a ser vuestro. Espero que sirva para todos los estudiantes y profesionales que quieran introducirse al maravilloso mundo de las obras, y en particular, a aquellos que tienen que luchar, día a día con el terreno donde se van a asentar.

Valencia, a 21 de julio de 2021

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Drenaje en excavaciones sobre acuíferos confinados: pozos de alivio

Figura 1. https://www.groundwatereng.com/dewatering-techniques/relief-wells

Los pozos de alivio, también conocidos como pozos de descarga de presión o pozos de purga, (pressure relief wells) se utilizan para reducir la presión intersticial en acuíferos confinados o en condiciones de suelo estratificado. Es típico de un estrato de baja permeabilidad (como una arcilla o roca de baja permeabilidad sin fisuras) situado sobre un acuífero confinado, lo cual puede provocar que el fondo de la excavación se vuelva inestable. Se trata del fenómeno conocido como “levantamiento de fondo” o “taponazo”, donde el peso del terreno no es capaz de equilibrar al empuje del agua.

Estos pozos se perforan normalmente antes de que la excavación hay alcanzado nivel piezométrico del acuífero. A medida que la excavación continúa, los pozos comenzarán a desbordarse, aliviando las presiones intersticiales asegurando su estabilidad. El agua que fluye de los pozos de descarga se bombea desde un sumidero. Se puede utilizar una capa granular de drenaje y una red de desagües para dirigir el agua a los sumideros y evitar que se estanque en la excavación y ablande el fondo. Es habitual que los pozos de descarga se perforen en cuadrícula dentro del recinto excavado, con una separación que dependerá del caudal previsto, pero que normalmente no es mayor a 5-10 m.

Los pozos de alivio también se clasifican como “pozos pasivos“, pues no necesitan un bombeo directo, más allá de las bombas de achique en los sumideros. Suelen presentar diámetros relativamente grandes (100 a 450 mm), que suelen rellenarse con material granular e incluso con tubo perforado. El material granular, normalmente una grava gruesa uniforme redondeada de tamaño nominal entre 10-20 mm, se introduce mediante una tubería tremie o incluso desde el propio nivel del suelo si esta grava tiene una clasificación muy uniforme, para evitar la segregación por tamaños. Son, por tanto, pozos simples de coste relativamente bajo de perforación, instalación y mantenimiento.

Los pozos de alivio son muy adecuados en recintos tablestacados o limitados por muros pantalla. Otras veces son drenajes permanentes en estructuras situadas sobre acuíferos confinados, como pudiera ser una estación subterránea de metro. En el caso de instalaciones permanentes, los pozos de descarga se instalan con rejillas y tuberías para permitir su limpieza.

Por último, cabe destacar que los pozos de alivio no pueden utilizarse donde la altura artesiana del agua en las capas permeables inferiores sea tal que el flujo en el interior de los pozos erosione el suelo inmediatamente debajo de ellos y a su alrededor.

Figura 3. Sistema de pozos de alivio (Cashman y Preene, 2012)

Os dejo un vídeo explicativo que os he grabado explicando este tipo de pozos.

REFERENCIAS:

CASHMAN, P.M.; PREENE, M. (2012). Groundwater Lowering in Construction: A Practical Guide to Dewatering, 2nd edition. CRC Press, Boca Raton, 645 pp.
POWERS, J.P. (1992). Construction dewatering: New methods and applications. Ed. Wiley et al., New York.
PREENE, M.; ROBERTS, T.O.L.; POWRIE, W. (2004). Groundwater Control – Design and Practice, 2nd Edition. Construction Industry Research and Information Association, CIRIA Report C750, London.
TOMLINSON, M.J. (1982). Diseño y construcción de cimientos. URMO, S.A. de Ediciones, Bilbao, 825 pp.
YEPES, V. (2020). Procedimientos de construcción de cimentaciones y estructuras de contención. Colección Manual de Referencia, 2ª edición. Editorial Universitat Politècnica de València, 480 pp. Ref. 328. ISBN: 978-84-9048-903-1.

Cursos:

Curso de procedimientos de contención y control del agua subterránea en obras de Ingeniería Civil y Edificación

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Necrológica: Han fallecido los profesores José Luis Ripoll García y Manuel Romana Ruiz

José Luis Ripoll (izquierda) y Manuel Romana (derecha)

La Escuela Técnica Superior de Ingeniería de Caminos, Canales y Puertos de Valencia ha perdido a dos de sus grandes catedráticos de geotecnia con un solo día de diferencia. Se trata de D. José Luis Ripoll García y D. Manuel Romana Ruiz. Tuve la suerte de tenerlos como profesores en las asignaturas de Geotecnia y Cimientos y de Cimentaciones Especiales. Estos días están siendo muy difíciles y dolorosos y como consecuencia, se nos están yendo los mejores. Voy a hacer una muy breve reseña de ambos, que seguro se quedará muy corta. Un abrazo muy fuerte y mis condolencias a familiares y amigos.

José Luis Ripoll García es Dr. Ingeniero de Caminos, Canales y Puertos, Catedrático Universidad Politécnica de Valencia, M. Sc. Ing. del terreno U. K., ex director general y consejero de Cubiertas y Mzov SA, Presidente de honor de Fundación Vodafone España, Vicepresidente de honor de la Corte de Arbitraje del Colegio de ICCP, Piloto de Aviación General. Medalla al Mérito en el Trabajo, en su categoría de Plata. Cruz de Oro de la Orden Civil de la Solidaridad Social. Miembro de la Academia Europea de Ciencias y Artes.

Manuel Romana Ruiz es Ingeniero de Caminos (1961) por la Escuela Técnica Superior de Ingenieros de Caminos, Canales y Puertos de Madrid y Doctor Ingeniero de Caminos (1971) por la Universidad Politécnica de Madrid. Durante sus estudios trabaja como becario de investigación en el Departamento de Materiales del Instituto Eduardo Torroja. En 1978 asume la Cátedra de Geotecnia y Cimientos, y desde 1980 es Catedrático de Ingeniería del Terreno en la Escuela Técnica Superior de Ingenieros de Caminos, Canales y Puertos de la Universidad Politécnica de Valencia, donde imparte docencia en las asignaturas de Geotecnia y Cimientos 2, Túneles y Obras Subterráneas, Mecánica de Rocas y Geotecnia aplicada a las Obras Hidráulicas. Su carrera profesional comienza en Dragados y Construcciones, a pie de obra (1961-1968) y continúa en INTECSA (1969-1986), donde desarrolla el Departamento de Geotecnia y Obras Subterráneas. En 1987 funda INGEOTEC, empresa consultora especializada en el proyecto de túneles y los estudios geotécnicos, y en 1999 STMR (Servicios Técnicos de Mecánica de Rocas). Ha sido Presidente de ambas empresas. Ha sido miembro de las Juntas Directivas de la Sociedad Española de Mecánica del Suelo (SEMSIG), Sociedad Española de Mecánica de las Rocas (SEMR) y de la Asociación Española de los Túneles (AETOS). Ha sido vicepresidente del Comité Español de Túneles de Carretera de ATC-PIARC y representante español en el Comité Internacional de Explotación de Túneles de PIARC, del que también fue Secretario de idioma español. Ha realizado numerosos proyectos de túneles de carretera, ferroviarios, de metro e hidráulicos actualmente en servicio (más de 500 km). Así mismo, ha sido autor de numerosas comunicaciones y textos sobre su especialidad.

Aquí dejo una entrevista que hicieron a D. Manuel con motivo del 50 aniversario de la Sociedad Española de Mecánica de Rocas.

Empuje de tierras, ¿mejor Coulomb o Rankine?

Figura 1. Coulomb y Rankine, autores de dos de los modelos clásicos de empuje de tierras.

El empuje de tierras sobre estructuras de contención ha sido un problema clásico en Geotecnia, pero que es complejo, pues existen numerosas incertidumbres asociadas al comportamiento de los distintos tipos de terreno. Tanto la dificultad en la determinación de las características mecánicas d

el terreno real como la complejidad en las hipótesis de cálculo han llevado a la utilización de simplificaciones útiles en una gran mayoría de casos. Las dos teorías clásicas en la estimación de los empujes del terreno se deben al francés Charles-Agustin de Coulomb (1736-1806) y al escocés William John Macquorn Rankine (1820-1872). Ambos métodos se sustentan en hipótesis diferentes y los resultados que proporcionan no coinciden, salvo en algún caso muy particular.

En cualquier libro de Geotecnia se puede comprobar cómo integrando las ecuaciones diferenciales de las condiciones de equilibrio interno de un elemento diferencial de un terreno horizontal, homogéneo, isótropo y con un comportamiento elástico, la tensión horizontal depende de la vertical. En el caso de que el terreno estuviera confinado lateralmente, con deformación lateral nula, la ley de Hooke proporciona una solución al problema, siendo la relación entre la tensión horizontal y la vertical constante. En cualquier caso, la condición de utilizar una ley de esfuerzo-deformación conveniente constituye el mayor obstáculo para obtener una solución exacta al problema.

Las presiones que soporta un muro o una pantalla reciben el nombre de empujes, que en el caso más general, será la suma del empuje hidrostático más el empuje efectivo ejercido por las partículas del terreno. Se define el coeficiente de empuje como la relación entre la tensión efectiva horizontal y la vertical, y en el caso de que no exista deformación lateral, se denomina coeficiente de empuje al reposo, K₀. De esta forma se podría calcular el empuje sobre un muro que no se deformara lo más mínimo. Sería el caso de un muro de sótano en edificación. Pero los muros no son infinitamente rígidos, se deforman, y dependiendo de si la deformación lateral es negativa (el terreno “se descomprime”) o positiva (el terreno “se comprime”), tendríamos los denominados empujes activos K_a, o pasivos K_p, (K_a<K₀<K_p). Para movilizar el empuje pasivo son necesarios movimientos del muro contra el terreno muy superiores a los necesarios para llegar a una situación de empuje activo. Cuando el empuje pasivo es favorable, debido a la imprecisión en la determinación de su valor real, por seguridad suele despreciarse su efecto o bien se aplica un coeficiente reductor (por ejemplo, de 1,5). Dejamos al lector investigar sobre este asunto en la literatura habitual.

Figura 2. Relación entre empuje del terreno y los movimientos necesarios para su desarrollo (Código Técnico de Edificación)

Lo que nos interesa en esta entrada es conocer las diferencias entre el método de Coulomb y el de Rankine e intentar interpretar cuándo sería mejor utilizar uno u otro método. Las fórmulas se pueden deducir de cualquier libro o manual de geotecnia. En ambos casos se puede generalizar la formulación al caso de terrenos cohesivos, presencia de nivel freático, cargas uniformes sobre el trasdós e inclinación del relleno tras el muro. Siendo σ’_v es la tensión efectiva vertical y c‘ la cohesión efectiva del terreno o relleno del trasdós, el empuje activo P_ase define como la resultante de los empujes unitarios σ’_a que puede determinarse mediante la siguiente fórmula:

y de forma análoga, el empuje pasivo P_p se define como la resultante de los empujes unitarios σ’_p que puede determinarse mediante:

La cohesión es un aspecto favorable para disminuir el empuje del terreno, pero si al final no se acaba desarrollando, nos deja del lado de la inseguridad; por tanto, como a veces es difícil estimar su efecto de forma adecuada, es habitual despreciarla para quedar del lado de la seguridad. Por tanto, se aconseja ser muy cuidadoso a la hora de considerar la cohesión.

Coulomb propuso un modelo para estimar los empujes del terreno planteando el equilibrio de una masa de terreno en forma de cuña al deformarse o moverse el muro. La rotura se produce a lo largo de dos planos, el formado por el interface suelo-muro y el plano de deslizamiento en el terreno. La cuña, formada por los dos planos, se comporta como un bloque rígido. De todas las cuñas posibles, una es la que produce el empuje activo máximo, y ese es el problema resuelto por este ingeniero francés en 1776. El método supone que las superficies de deslizamiento son planas, pero esta hipótesis es muy discutible en el caso del empuje pasivo. El problema queda resuelto para un muro cualquiera, con un trasdós que no necesita ser vertical, y un terreno con una determinada inclinación y con unas cargas sobre su superficie. Se supone conocido el peso específico del terreno, el ángulo de rozamiento interno y el ángulo de rozamiento muro-suelo. Es actualmente el método más empleado para el diseño de muros por métodos de equilibrio límite. Hoy día se emplea con gran efectividad en el cálculo de muros de gravedad, lo que permite considerables ahorros de material. Las fórmulas que siguen indican los coeficientes de empuje activo y pasivo, con las figuras que definen cada uno de los ángulos correspondientes:

El método de Rankine (1857) es más elegante desde el punto de vista matemático, explicando el empuje en términos de rotura por cortante del terreno. Se obtienen los empujes partiendo de un semiespacio infinito que se encuentra en “estado de Rankine“, es decir, un estado de equilibrio plástico y en donde el muro no produce ninguna perturbación. Se supone que el terreno es homogéneo e isótropo y en estado de equilibrio plástico, es decir, se acepta que toda la masa en el trasdós del muro está en situación de rotura y, por tanto, en cualquier punto el estado tensional pertenece a un círculo de Morh que es tangente a la línea de rotura de este suelo; además, como hipótesis adicional, no hay variación de tensiones en los puntos de cualquier plano paralelo a la superficie del semiespacio. Este modelo puede resultar un tanto conservador, pues solo considera el ángulo de rozamiento interno del terreno, olvidando el efecto favorable del rozamiento entre el muro y el terreno. Este método tiene muchas aplicaciones prácticas, por ejemplo, en muros ménsula, donde la suposición de Rankine no supone grandes desventajas y simplifica enormemente los cálculos. El cálculo de empujes sobre un muro con el modelo de Rankine se reduce a obtener las presiones efectivas a la profundidad correspondientes y aplicar las fórmulas correspondientes. De esta forma es muy sencillo calcular terrenos estratificados y considerar la existencia de una carga uniforme en coronación. Además, el método permite estimar si existen grietas de tracción y su profundidad en un terreno que sea cohesivo. Los coeficientes de empuje activo y pasivo para un terreno que forma un ángulo i con la horizontal teniendo en cuenta que la resultante forma un ángulo i con la horizontal, son los siguientes:

Aplicando el teorema de los estados correspondientes de Caquot, se puede generalizar la teoría de Rankine a suelos cohesivos: “Si a un suelo con cohesión que está en situación límite de rotura, simultáneamente le quitamos la cohesión y sumamos a todas las tensiones un término (c’ · cotg Φ’), el suelo sigue estando en la misma situación límite de rotura” (y se le aplican las hipótesis de los suelos sin cohesión).

Figura 3. Círculo de Mohr considerando suelos cohesivos

De las fórmulas deducidas para el empuje activo y pasivo, las fórmulas en ambos modelos coinciden únicamente en el caso de un trasdós vertical del muro, no hay rozamiento suelo-estructura y la superficie del terreno es horizontal. En este caso, los coeficientes de empuje activo y pasivo son los siguientes:

Resumiendo los aspectos básicos expuestos anteriormente, podríamos decir lo siguiente:

En caso de terrenos estratificados, la inclinación del plano de deslizamiento depende de cada terreno, con lo que el problema puede ser indeterminado si utilizamos el modelo de Coulomb. En este caso, Rankine es de más fácil formulación, que suele ser recomendable en el caso de muros ménsula.
El método de Coulomb no tiene en cuenta la presencia de grietas de tracción, por lo que con terrenos cohesivos el cálculo de la profundidad de estas grietas se debe hacer con Rankine.
Si no existe cohesión en el terreno ni adherencia entre muro y terreno, con la teoría de Coulomb se puede determinar que la resultante del empuje activo está situada, desde la base del muro, a un tercio de la altura del muro. Si no es así, entonces el método no proporciona directamente la posición del empuje.
El método de Rankine es difícil de aplicar con geometrías mínimamente complejas (trasdós quebrado, superficies del terreno en el trasdós no planas, cargar arbitrarias sobre éste último) y no es mucho más preciso que el método de Coulomb para estos casos.
El método de Coulomb no estima bien el empuje pasivo, pues la superficie real de rotura no es plana (se asemeja a una espiral logarítmica) y la distribución de empujes difiere bastante de la triangular, proporcionando valores sobredimensionados (del lado de la inseguridad). El método de Rankine es más conservador para el cálculo de empujes pasivos.
El método de Rankine no considera el rozamiento entre el muro y el terreno, lo cual es conservador. Es un aspecto importante en muros de gravedad, cuyos empujes activos se prefieren calcular con Coulomb.
En el método de Coulomb permite la consideración de sobrecargas en el trasdós de cualquier tipo (constante, puntual, triangular, etc.) siempre que sean indefinidas en el sentido longitudinal del muro, pues basta introducirlas en las ecuaciones de equilibrio. Con Rankine es sencillo si se trata de una sobrecarga constante.

REFERENCIAS:

GARCÍA VALCARCE, A. (dir.) (2003). Manual de edificación: mecánica de los terrenos y cimientos. CIE Inversiones Editoriales Dossat-2000 S.L. Madrid, 716 pp.
GONZÁLEZ CABALLERO, M. (2001). El terreno. Edicions UPC, Barcelona, 309 pp.
IZQUIERDO, F.A. (2001). Cuestiones de geotecnia y cimientos. Editorial Universidad Politécnica de Valencia, 227 pp.
LAMBE, T.W.; WHITMAN, R.V. (1996). Mecánica de suelos. Limusa, México, D.F., 582 pp.
MINISTERIO DE FOMENTO (2002). Guía de Cimentaciones. Dirección General de Carreteras.
MINISTERIO DE LA VIVIENDA (2006). Código Técnico de la Edificación
YEPES, V. (2020). Procedimientos de construcción de cimentaciones y estructuras de contención. Colección Manual de Referencia, 2ª edición. Editorial Universitat Politècnica de València, 480 pp. Ref. 328. ISBN: 978-84-9048-903-1.
YEPES, V. (2023). Maquinaria y procedimientos de construcción. Problemas resueltos. Colección Académica. Editorial Universitat Politècnica de València, 562 pp. Ref. 376. ISBN 978-84-1396-174-3

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Paradoja de Zenón en la parsimonia del asiento de los suelos saturados

Figura 1. Inclinación de la torre de Pisa

Una de las paradojas que planteó el filósofo Zenón de Elea es que si para ir a un lugar recorres primero la mitad de la distancia, luego la mitad de la distancia que te queda por recorrer, y así hasta el infinito, nunca llegarás a tu destino, aunque estés toda la vida andando. Esta paradoja se solucionó matemáticamente en el siglo XIX al aceptar que la suma de 1/2 + 1/4 + … suman 1. Pues bien, un terreno saturado al que sometemos a una carga va a asentar de forma indefinida, pero no superará un valor tope determinado. Veamos esto con mayor detalle.

En un artículo anterior vimos hablamos del Principio de Terzaghi, por el cual un terreno se deforma solo cuando existe un cambio en sus tensiones efectivas. Cuando se carga un terreno saturado, éste tiene la costumbre provocar asientos que se incrementan con el tiempo, siempre que sea posible el drenaje. Esto plantea la pregunta de si los asientos crecerán de forma indefinida con el tiempo. Afortunadamente, el asiento tiende asintóticamente a una magnitud última a la cual se llegará, eso sí, en tiempo infinito.

Pero empecemos por el principio. En presencia de un sólido homogéneo, isótropo y linealmente elástico, la teoría de la elasticidad nos permite conocer perfectamente la deformación que tendrá ante un incremento de cargas. Para ello basta conocer el módulo de elasticidad E y el coeficiente de Poisson ν. Es más, si estamos ante este tipo de terreno y conocemos las ecuaciones de Hooke en términos efectivos (es decir, conocemos E‘ y γ’, obtenidos en suelo drenado, a largo plazo), entonces tenemos herramientas para averiguar la deformación del terreno, tal y como vimos en el artículo que donde hablábamos de los asientos de cargas rectangulares en el semiespacio de Boussinesq. Este método sería válido para cargas de servicio o de trabajo, alejadas de la carga de rotura (factor de seguridad del orden de 3), que probablemente generen asientos elásticos. El método elástico será tanto más aceptable cuanto más se asemeje el comportamiento del suelo al del sólido lineal-elástico, como es el caso de los suelos granulares o las arcillas fuertemente sobreconsolidadas, bajo presiones normales de cimentación.

Sin embargo, no vamos a tener tanta suerte. El comportamiento del suelo es más complejo. De hecho, la deformación ocurrirá, tal y como se ha comentado anteriormente, cuando las presiones efectivas empiecen a cambiar. Y eso tendrá lugar si se permiten disipar las presiones intersticiales del terreno. Por tanto, las deformaciones van a depender, entre otros factores, de la permeabilidad. Terrenos altamente permeables, como gravas o arenas, van a deformar rápidamente, puesto que el agua drenará con mucha facilidad. Pero terrenos más impermeables como las arcillas, el proceso se dilatará en el tiempo. Es el fenómeno conocido como consolidación.

Por tanto, ante un terreno saturado, tenemos tres tipos de consolidación. La consolidación inicial la provoca un aumento de la presión total, que provoca un cambio de volumen debido a efectos como la disolución de las burbujas de aire, el cierre de fisuras o la reordenación de las partículas, entre otras posibles causas. La consolidación primaria, es provocada por el aumento de la presión efectiva como consecuencia de la disipación de las sobrepresiones intersticiales. Por último, la consolidación secundaria se produce a tensión efectiva constante, es decir, una vez disipada la sobrepresión intersticial y se debe a factores como la fluencia por desplazamientos y reorientaciones de partículas, o bien a la descomposición de la materia orgánica del suelo, entre otras posibles causas.

Figura 2. Curva de consolidación de un suelo saturado.

Para determinar tanto la magnitud de la deformación de un suelo al aumentar la tensión efectiva a la que está sometido (curva edométrica), como la velocidad a la que ocurre el asiento de consolidación (curva de consolidación), se utiliza el ensayo edométrico. De este ensayo y sus características hablaremos en otros artículos.

Pero aquí lo que queremos es ver cómo evolucionan los asiento con el tiempo durante el proceso de consolidación. En un proceso unidimensional, la ecuación que gobierna dicho proceso es la siguiente:

donde C_v es el denominado coeficiente de consolidación vertical, que depende del nivel de tensiones existente y cuyas unidades son [L²]/[T]. Este coeficiente en una arcilla puede deducirse de un ensayo edométrico de una muestra inalterada. Su valor tipo oscila entre 0,4 x 10^-4 y 3 x 10^-3cm²/s, y los valores deducidos in situ oscilan entre 0,7 x 10^-4 y 250cm²/s (González Caballero, 2001).

Si definimos como grado de consolidación U la relación entre el asiento experimentado en un instante por el suelo respecto al asiento total, podemos utilizar U como variable auxiliar adimensional para resolver la ecuación diferencial anterior.

Si llamamos factor de tiempo a T_v, éste se encuentra relacionado con U. La solución simplificada de la ecuación diferencial, suponiendo que el incremento de presión total es uniforme o lineal en el caso del doble drenaje, nos lleva a dos ecuaciones sencillas, que son las siguientes:

Estas expresiones las hemos dibujado en la Figura 3, donde se relaciona U con T_v. Se puede observar que para el grado de consolidación del 100%, el factor de tiempo se hace infinito. No obstante, se puede considerar que un factor de tiempo T_v = 2 corresponde prácticamente al final de la consolidación primaria.

Figura 3. Factor de tiempo en función del grado de consolidación

Además, el coeficiente de consolidación vertical C_v está relacionado con el factor de tiempo T_v, con la distancia libre de drenaje d y con el tiempo t a través de la siguiente expresión:

Por tanto, se puede saber el tiempo que tardará en asentar un suelo saturado para alcanzar un grado de consolidación determinado conociendo la distancia libre de drenaje y el coeficiente de consolidación vertical. Los cálculos pueden realizarse rápidamente utilizando la gráfica de la Figura 4. Se ha dibujado el eje vertical en escala logarítmica. Cada función indica una longitud libre de drenaje distinta.

Figura 4. Relación entre el producto del coeficiente de consolidación y el tiempo con el grado de consolidación y la distancia libre de drenaje.

Vamos a hacer un cálculo aproximado utilizando la Figura 4. Si suponemos una arcilla con un coeficiente de consolidación C_v = 1,0 m²/año, en el periodo de 1 año, con una longitud de drenaje de 1 m, se habrá superado más del 90% del asiento previsto, pero si la longitud de drenaje es de 2 m, no llegaremos al 60% del asiento.

Se deja al lector curioso la demostración de que si la longitud de drenaje la dividimos por n, entonces el tiempo que se tardará en alcanzar el mismo grado de consolidación se divide por n² . Así, por ejemplo, una capa de arcillas dispuesta entre dos capas de material granular tardará en alcanzar un mismo asiento en la cuarta parte del tiempo que si dicha capa estuviese dispuesta entre una capa granular y otra impermeable.

Referencias:

DAS, B. (2005). Fundamental of Geotechnical Engineering – 2nd ed, Technomic Publishing Co.
GONZÁLEZ CABALLERO, M. (2001). El terreno. Edicions UPC, 309 pp.
GONZÁLEZ DE VALLEJO, L.I. et al. (2004). Ingeniería Geológica. Pearson, Prentice Hall, Madrid.
IZQUIERDO, F.A. (2001). Cuestiones de geotecnia y cimientos. Editorial Universidad Politécnica de Valencia, 227 pp.
YEPES, V. (2020). Procedimientos de construcción de cimentaciones y estructuras de contención. Colección Manual de Referencia, 2ª edición. Editorial Universitat Politècnica de València, 480 pp. Ref. 328. ISBN: 978-84-9048-903-1.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Asientos de cargas rectangulares en el semiespacio de Boussinesq

Joseph Valentin Boussinesq. https://es.wikipedia.org/wiki/Joseph_Boussinesq

El matemático francés Joseph Valentin Boussinesq (1842-1929) desarrolló en 1885 una expresión matemática para obtener el incremento de esfuerzo en una masa semi-infinita de suelo debido a la aplicación de una carga puntual en su superficie. Dicha expresión se puede integrar para obtener soluciones para áreas cargadas. Para ello se supone que dicho semi-espacio es infinitamente grande, siendo un medio homogéneo, elástico lineal e isótropo.

Sabiendo que el terreno dista de ser un semiespacio de Boussinesq, se puede aplicar la Teoría de la Elasticidad para estimar los asientos producidos por una carga rectangular como pudiera ser la de una losa de cimentación o la de una zapata. Estos asientos pueden producirse instantáneamente o bien con el paso del tiempo, los llamados asientos de consolidación. El modelo elástico proporciona soluciones para una gran variedad de problemas, y si bien el comportamiento del terreno no es generalmente elástico, hoy día se dispone de una amplia experiencia respecto al uso y limitaciones.

Una de las grandes ventajas que presenta la hipótesis de que el terreno es elástico lineal es la validez del principio de superposición, cuyo enunciado dice que “si se tienen dos estados de tensiones y deformaciones correspondientes, al estado tensional suma le corresponde el estado de deformaciones suma“.

Para el cálculo de las deformaciones con la teoría elástica es necesario conocer el módulo de elasticidad o módulo de Young, E, así como el coeficiente de Poisson, γ. Sin embargo, según el Principio de Terzaghi, “las deformaciones en suelos se deben a la variación de las tensiones efectivas“, por lo que las ecuaciones de Hooke deben escribirse en términos efectivos. Es decir, se deben utilizar E‘ y γ‘, obtenidos en condiciones drenadas del suelo, es decir, a largo plazo. Este método sería válido para cargas de servicio o de trabajo, alejadas de la carga de rotura (factor de seguridad del orden de 3), que probablemente generen asientos elásticos. El método elástico será tanto más aceptable cuanto más se asemeje el comportamiento del suelo al del sólido lineal-elástico, como es el caso de los suelos granulares o las arcillas fuertemente sobreconsolidadas, bajo presiones normales de cimentación.

En las Tablas D.23 y D.24 del Código Técnico de Edificación se recogen valores orientativos de los módulos de elasticidad E‘ y del coeficiente de Poisson γ‘. En algunos casos no es posible trabajar con tensiones efectivas, por lo que en Geotecnia se hace en totales, utilizando unos parámetros elásticos en totales o aparentes.

Como un suelo saturado responde a corto plazo sin variar su volumen, ello supone un coeficiente de Poisson de 0,5 trabajando en tensiones totales. En ese caso se utiliza un módulo de elasticidad E_udenominado “módulo de elasticidad sin drenaje“. Este módulo es de difícil determinación, aunque se suele considerar E_u = 500·C_u,pero con errores del orden del 50%. Skempton recomienda adoptar como E_u el módulo secante correspondiente a una tensión aplicada igual al 65% de la tensión de rotura (coeficiente de seguridad F=3 en cimentaciones superficiales). Como los esfuerzos cortantes son iguales en tensiones totales o en efectivas, los módulos de rigidez G coincidirán, lo cual permite deducir E_u conocidos E‘ y γ‘ con la siguiente expresión:

Llegado a este punto, ¿cómo calculamos las deformaciones verticales al aplicar una carga sobre el terreno? Llamaremos “asientos” a dicha deformación vertical, distinguiéndose los “asientos instantáneos” los que ocurren a corto plazo, es decir, en condiciones sin drenaje. A ellos habría que sumar los asientos a largo plazo, en condiciones de drenaje, que son los “asientos de consolidación“. Por tanto, los asientos totales se calcularán con E‘ y γ‘ (condiciones drenadas, a largo plazo) y los asientos instantáneos con E_u y con γ = 0,5. La diferencia serán los asientos diferidos (semejantes a los de consolidación). Veamos ahora los cálculos.

Para cargas flexibles con forma circular, cuadrada o rectangular, el asiento bajo el centro de las mismas se obtiene con la siguiente expresión:

En la que B es el lado menor del área cargada y I_Ses un coeficiente de influencia que vale I_S=1 en cargas circulares y I_S=1,122 en cargas cuadradas. Para cargas rectangulares se puede obtener el asiento en una esquina con la fórmula anterior pero adoptando un coeficiente de influencia que viene dado por esta expresión, donde n=L/B:

El Cuadro 1 y la Figura 1 nos dan valores para este coeficiente de influencia.

Cuadro. Valores del coeficiente de influencia en función de L/B

Figura 1. Coeficiente de influencia en función de L/B

Aplicando el principio de superposición que permite la teoría elástica, el lector puede comprobar de forma sencilla que el asiento en el centro es el doble que en una de sus esquinas (Figura 2).

Figura 2. Principio de superposición para calcular el asiento en el centro de una carga rectangular por suma de cuatro asientos de cargas rectangulares en su esquina

Por último, en el caso de una carga rígida, como sería el caso de muchas zapatas, se considera que el asiento es uniforme e igual, aproximadamente, a 0,8 veces el asiento que se obtendría en el centro si fuese una zapata flexible. Es fácil comprobar que dicho asiento valdría.

Como recordatorio, habría que decir que la carga que se aplica en superficie en las fórmulas anteriores se debería cambiar por la carga o tensión neta en el caso de que la carga se aplique tras una excavación previa. Es decir, la carga a utilizar en las fórmulas es la diferencia entre la tensión aplicada en superficie y la existente en el terreno a la profundidad del plano de cimentación. Dicho de otra forma, hay que quitar de la carga total aplicada la correspondiente al peso del terreno excavado.

Se deja al lector inquieto calcular el asiento en el centro de una zapata rectangular de 2,50 m x 5,00 m que se cimenta sobre unas arcillas con un peso específico saturado de 22 kN/m³, con un módulo de elasticidad efectivo de 92,00 MPa y un coeficiente de Poisson efectivo de 0,5. La zapata se apoya a 2,00 m de profundidad y el peso propio que se le transmite es de 100 kN/m².

Referencias:

DAS, B. (2005). Fundamental of Geotechnical Engineering – 2nd ed, Technomic Publishing Co.
GONZÁLEZ CABALLERO, M. (2001). El terreno. Edicions UPC, 309 pp.
GONZÁLEZ DE VALLEJO, L.I. et al. (2004). Ingeniería Geológica. Pearson, Prentice Hall, Madrid.
IZQUIERDO, F.A. (2001). Cuestiones de geotecnia y cimientos. Editorial Universidad Politécnica de Valencia, 227 pp.
YEPES, V. (2020). Procedimientos de construcción de cimentaciones y estructuras de contención. Colección Manual de Referencia, 2ª edición. Editorial Universitat Politècnica de València, 480 pp. Ref. 328. ISBN: 978-84-9048-903-1.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

El efecto Renard, o por qué un suelo parece que entra en ebullición: Sifonamiento

Figura 1. Arenas movedizas. https://churbuck.com/category/clamming/page/2/

Cuando existe un flujo ascendente de agua en un terreno, la corriente circula en sentido contrario al peso del terreno. Este empuje puede ser tan algo que supere al peso del terreno, con lo cual tenemos la impresión que el terreno se ha licuado y se comporta como un líquido en ebullición. Este efecto, muy estudiado en cualquier libro de geotecnia, tiene lugar cuando las tensiones efectivas se anulan. Se produce el fenómeno del sifonamiento o licuación, también llamado “efecto Renard”. En este caso, una arena, por ejemplo, pierde su consistencia y parece que entre en ebullición. Esto se debe a que un suelo sin cohesión pierde completamente su resistencia al corte y pasa a comportarse como un fluido.

Resulta sencillo demostrar que este fenómeno ocurre cuando se alcanza un gradiente crítico, cuyo valor es el cociente entre el peso específico sumergido del suelo y el peso específico del agua. Este valor se aproxima en muchos casos a la unidad. Cualquier objeto que se sitúe sobre un terreno con licuación que tenga un peso específico superior al del la mezcla fluida de terreno y agua, se hundirá; esto es especialmente importante si tenemos maquinaria dentro de la excavación o existen cimentación que se apoye en esa zona. Se trata del conocido fenómeno de las arenas movedizas.

Este problema es importante cuando tenemos que excavar bajo nivel freático una profundidad “h” (ver Figura 2). Una forma de solucionar evitar el sifonamiento consiste en utilizar tablestacas o ataguías que tengan una longitud de empotramiento “x” suficiente. En este caso, la línea de filtración más corta del agua tiene una longitud igual a h+2x.

Figura 2. Longitud de empotramiento para evitar el sifonamiento

Supongamos que nos dan como datos el peso específico de las partículas sólidas de un suelo “γ_s ” y su porosidad “n“. El peso específico del agua es “γ_w“. Vamos a considerar un coeficiente de seguridad “η“. Como el gradiente es h/(h+2x), se puede comparar con el gradiente crítico dividido por su coeficiente de seguridad. De este modo, es fácil demostrar que la longitud de empotramiento es:

En la Figura 3 se representa la evolución del empotramiento en función de la profundidad de la excavación bajo nivel freático y de la porosidad del suelo. Se ha supuesto γ_s = 2,65 t/m³ y un coeficiente de seguridad η = 3. Es fácil comprobar la relación lineal entre el empotramiento y la altura del nivel freático sobre la excavación. Además, cuanto más poros presenta el terreno, más empotramiento es necesario.

Figura 3. Profundidad de empotramiento de una tablestaca para evitar el sifonamiento

Respecto al coeficiente de seguridad frente al sifonamiento, el Código Técnico de la Edificación (CTE), en su Documento Básico SE-C Cimientos, se indica que, en el caso de las pantallas, el coeficiente de seguridad será η = 2.

Nota muy importante: una cosa es la profundidad mínima de empotramiento para evitar el sifonamiento y otra bien diferente es calcular el empotramiento necesario de una tablestaca para soportar los esfuerzos de empuje a los que está sometido. Por tanto, el empotramiento real será el mayor de los dos valores. Se recomienda siempre efectuar con detalle los cálculos geotécnicos y estructurales necesarios. Y sobre todo, utilizar el sentido común.

Referencias:

DAS, B. (2005). Fundamental of Geotechnical Engineering – 2nd ed, Technomic Publishing Co.
GONZÁLEZ DE VALLEJO, L.I. et al. (2004). Ingeniería Geológica. Pearson, Prentice Hall, Madrid.
YEPES, V. (2020). Procedimientos de construcción de cimentaciones y estructuras de contención. Colección Manual de Referencia, 2ª edición. Editorial Universitat Politècnica de València, 480 pp. Ref. 328. ISBN: 978-84-9048-903-1.

Cursos:

Curso de Procedimientos de Construcción de cimentaciones y estructuras de contención en obra civil y edificación.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

La magia de las tensiones efectivas en geotecnia

Karl von Terzaghi (1883 – 1963) ://es.wikipedia.org/wiki/Karl_von_Terzaghi

Os presento uno de los conceptos básicos utilizados en geotecnia que, en ocasiones, complica a muchos de mis estudiantes cuando en la asignatura Procedimientos de Construcción explicamos algunos aspectos de la mejora de terrenos (columna de grava, precarga, drenes verticales, etc.). Se trata del concepto de “tensiones efectivas”, que hoy es sencillo, pero que confundió a numerosos ingenieros durante mucho tiempo.

La ley de elasticidad Hooke, donde la aplicación de una fuerza supone una deformación proporcional a la misma, desde luego no era aplicable directamente a muchos problemas que los ingenieros tenían con el terreno. Desde siempre se conoce que el comportamiento mecánico del suelo es algo complejo, pero era sorprendente, por ejemplo, que una carga aplicada sobre un terreno con nivel freático elevado, no se deformase. Y lo más sorprendente, es que, al cabo de cierto tiempo, sin modificar el estado de cargas, el terreno se deformara “por arte de magia”.

Este problema ingenieril traía de cabeza a muchos ingenieros hasta los primeros años del siglo XX. Si se analiza un suelo desde el punto de vista “microscópico”, la transmisión de esfuerzos se realiza mediante cadenas de partículas, unas apoyadas con otras. Lo que es peor, si este suelo es de partículas tan finas como son las arcillas, la fuerza de gravedad pierde importancia frente a las fuerzas fisico-químicas. La solución es entender la mecánica del suelo como si fuera un medio continuo, es decir, desde el punto de vista “macroscópico”. Tal simplificación necesita un marco teórico de partida que fue postulado por uno de los grandes genios y padre de la mecánica de suelos: Karl von Terzaghi (Praga, 2 de octubre de 1883 – Winchester, Massachusetts, 25 de octubre de 1963).

Su aportación genial fue formular un postulado acerca de lo que denominó como “tensiones efectivas“. Como todo postulado que se precie, se trata de una proposición no evidente por sí misma, ni demostrada, pero que se acepta, ya que no existe otro principio al que pueda ser referida. De todos modos, las evidencias empíricas del correcto funcionamiento de este postulado hace que hoy día se admita en el campo de la mecánica de suelos porque permite explicar multitud de problemas geotécnicos. Terzaghi definió el concepto de tensiones efectivas, en 1923, partiendo de resultados experimentales. De forma muy simple, diremos que las tensiones efectivas que actúan en el terreno son el exceso de tensión sobre la presión intersticial del agua presente en él. Y lo más importante de todo ello es que son las tensiones efectivas las que pueden provocar cambios en la deformación del terreno. Pero vamos a reproducir (González de Vallejo et al., 2004) las dos partes fundamentales del enunciado de su postulado, según las propias palabras de Terzaghi:

“Las tensiones en cualquier punto de un plano que atraviesa una masa de suelo pueden ser calculadas a partir de las tensiones principales totales σ₁, σ₂ y σ₃ , que actúan en ese punto. Si los poros del suelo se encuentran rellenos de agua bajo una presión u, las tensiones principales totales se componen de dos partes. Una parte, u, llamada presión neutra o presión intersticial, actúa sobre el agua y sobre las partículas sólidas en todas direcciones y con igual intensidad. Las diferencias σ’₁ = σ₁ – u, σ’₂ = σ₂ – u, σ’₃ = σ₃ – u representan un exceso de presión sobre la presión neutra u, y actúan exclusivamente en la fase sólida del suelo. Estas fracciones de las tensiones principales totales se denominan tensiones efectivas.

Cualquier efecto medible debido a un cambio de tensiones, tal como la compresión, la distorsión o la modificación de la resistencia al corte de un suelo, es debido exclusivamente a cambios en las tensiones efectivas”.

Podemos sacar varias conclusiones directamente de este postulado:

Si en un suelo saturado no hay cambios de volumen ni de distorsión, eso significa que las tensiones efectivas no han cambiado.
Como el agua no es capaz de soportar tensiones tangenciales, las que existan en un suelo saturado la debe absorber el esqueleto sólido del suelo.
Si a un suelo saturado se le permite el drenaje (disipación de la tensión intersticial), entonces este suelo se deforma y se modifica su resistencia a corte. Al fenómeno se denomina consolidación.

Como entretenimiento práctico podéis deducir cómo la tensión efectiva en un punto de un estrato situado bajo nivel freático es igual al producto de la profundidad del punto en el estrato multiplicado por el peso específico sumergido del material de dicho estrato. Asimismo, si existen distintos estratos, es la suma de las alturas de los posibles estratos por sus correspondientes pesos específicos sumergidos.

Referencias:

DAS, B. (2005). Fundamental of Geotechnical Engineering – 2nd ed, Technomic Publishing Co.
GONZÁLEZ DE VALLEJO, L.I. et al. (2004). Ingeniería Geológica. Pearson, Prentice Hall, Madrid.
YEPES, V. (2020). Procedimientos de construcción de cimentaciones y estructuras de contención. Colección Manual de Referencia, 2ª edición. Editorial Universitat Politècnica de València, 480 pp. Ref. 328. ISBN: 978-84-9048-903-1.

Cursos:

Curso de Procedimientos de Construcción de cimentaciones y estructuras de contención en obra civil y edificación.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Normativa peruana sobre suelos y cimentaciones

¿Es bueno aplicar una norma que se utiliza en un país distinto al nuestro? Esta pregunta se repite muchas veces cuando se abren debates, sobre todo en España sobre el uso de los Eurocódigos (véase el caso de la Instrucción de Hormigón Estructural). Es evidente que en cada país se utiliza un tipo de norma que, si bien tiende a unificar aquellas partes comunes asentadas en el ámbito técnico y científico, en numerosas ocasiones se adapta a la idiosincrasia del país y sus circunstancias. Aspectos como el riesgo sísmico o geológico, materiales y procedimientos constructivos más empleados, sistemas de control de calidad en el sector, etc., hacen que se particularicen o resalten determinados aspectos de cada norma. No obstante todo lo anterior, sería un gran avance unificar normas y criterios, aunque en cada país se adoptaran coeficientes de seguridad o parámetros de diseño particulares.

En este caso os presento la Resolución Ministerial nº 406-2018-vivienda por la que se publica la Norma Técnica E.050 sobre “Suelos y Cimentaciones” del Perú. Agradezco el documento a Christian Martín Torres Delgado. Es una de las ventajas de estar conectado a las redes sociales, en este caso LinkedIn, que permiten compartir conocimiento técnico de forma ágil. Espero que el documento os sea de interés.

Descargar (PDF, 2.72MB)

Columnas de gravas

Figura 1. Tratamiento del terreno con columnas de grava en función de la altura del terraplén. Fuente: Carlos Oteo

Las columnas de grava constituyen un método de mejora de terrenos cohesivos blandos mediante la rigidización que produce la introducción de columnas de grava en los orificios creados por el vibrador o equipo de pilotaje convencional, según sea el método de ejecución escogido. Aumenta la capacidad portante del terreno, la estabilidad al deslizamiento en terraplenes, acelera el proceso de consolidación del terreno (constituyen drenes verticales) y provoca una reducción de los asientos en servicio. Se aplica sobre arenas limosas, limos, limos arcillosos, arcillas y rellenos heterogéneos.

En casos en los que además de una preconsolidación es necesario un refuerzo del terreno, como en el caso de terraplenes elevados, que precisan de terrenos portantes de mayor resistencia, la inclusión de columnas de grava permite solucionar el problema.

Las columnas de grava aparecieron como una extensión de las técnicas de vibrocompactación profunda de suelos finos. Puede realizarse mediante un pilotaje convencional o mediante el uso de vibradores especiales (Figura 2). La técnica mediante pilotaje convencional puede ser por sustitución o por desplazamiento. La vibrosustitución o vibrodesplazamiento, se aplica en terrenos cohesivos (contenido de finos > 12%), y supone la sustitución del terreno por un material granular de aportación.

Figura 2. Ejecución de columnas de grava

No obstante, también se puede aplicar la vibración profunda en suelos granulares (contenidos de finos < 12%), normalmente con vibradores específicos de baja frecuencia y usando agua a presión para facilitar el hincado, lo que produce una licuación parcial del terreno y su densificación. Este procedimiento se denomina vibroflotación o vibrocompactación. El terreno no se sustituye, rellenándose el cono de hundimiento alrededor del vibrador con el terreno, no siendo propiamente una columna de grava. Sin embargo, a veces se aporta material granular de mayor calidad transportado a la obra, por ejemplo, árido de machaqueo de 20-40 mm, por lo que se podría hablar en este caso de una columna de grava.

En la Figura 3 se puede observar el ámbito de aplicación de las columnas de grava frente a la vibrocompactación en función del tipo de terreno. En las arenas se comprueba que existe una zona de transición entre ambas técnicas de mejora de terrenos mediante vibración profunda.

Figura 3. Ámbito de aplicación de las técnicas

Como limitación de esta técnica, en suelos blandos originales que tengan baja capacidad portante para soportar la resistencia lateral que le pueden exigir las columnas cargadas, con resistencias a corte sin drenaje c_u≤ 0.015 MPa.

Figura 4. Relaciones asiento-tiempo en terraplenes con diferentes tratamientos. Fuente: Carlos Oteo

Las recomendaciones más importantes para ejecutar una columna de grava serían las siguientes:

Tamaño entre 5 y 40 mm para la grava, con un ángulo de rozamiento interno entre 38º y 40º, sin ser friable (valores menores al 30-35% en el ensayo de los ángeles)
Separación entre columnas de 2 a 10 m, en malla regular
Diámetros entre 40 y 120 cm, dependiendo del terreno
Profundidad que puede llegar a 37 m, aunque lo normal es no pasar de 20 m
El cálculo de las columnas de grava suele hacerse con el método de Priebe (1995), que obtiene los parámetros del suelo equivalentes mejorados. Con este método deben utilizarse valores conservadores, por ejemplo, un grado de rozamiento de 40º, y garantizar una correcta ejecución de las columnas para que, por ejemplo, el ángulo de rozamiento de la columna sea superior al supuesto.

A continuación os dejo un catálogo de Terratest sobre columnas de grava que creo os puede ampliar la información al respecto.

Descargar (PDF, 3.14MB)

Dejo también un artículo de Juan Manuel Fernández Vincent sobre las columnas de grava.

Descargar (PDF, 1MB)

Os paso varios vídeos de esta técnica de mejora de terrenos. Espero que os sean útiles.

Referencias:

MARTÍ, J.V.; GONZÁLEZ, F.; YEPES, V. (2004). Temas de procedimientos de construcción. Mejora de terrenos. Editorial de la Universidad Politécnica de Valencia. Ref. 2004.844.

MONTEJANO, J.C. (2017). Ejecución de columnas de grava como refuerzo de la cimentación de un parque eólico en Nouakchott, Mauritania. Interempresas.net

PRIEBE, H.J. (1995). Design of vibro replacement. Ground Engineering, 28(10):31-37.

YEPES, V. (2020). Procedimientos de construcción de cimentaciones y estructuras de contención. Colección Manual de Referencia, 2ª edición. Editorial Universitat Politècnica de València, 480 pp. Ref. 328. ISBN: 978-84-9048-903-1.

Cursos:

Curso de Procedimientos de Construcción de cimentaciones y estructuras de contención en obra civil y edificación.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.