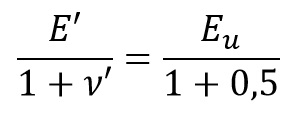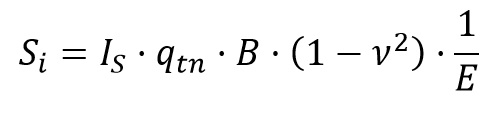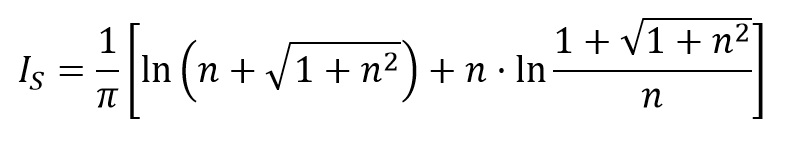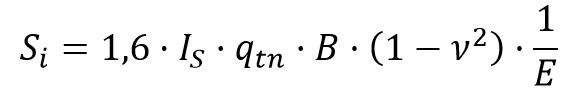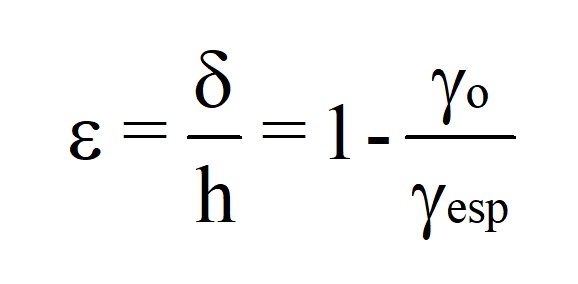El matemático francés Joseph Valentin Boussinesq (1842-1929) desarrolló en 1885 una expresión matemática para obtener el incremento de esfuerzo en una masa semi-infinita de suelo debido a la aplicación de una carga puntual en su superficie. Dicha expresión se puede integrar para obtener soluciones para áreas cargadas. Para ello se supone que dicho semi-espacio es infinitamente grande, siendo un medio homogéneo, elástico lineal e isótropo.
Sabiendo que el terreno dista de ser un semiespacio de Boussinesq, se puede aplicar la Teoría de la Elasticidad para estimar los asientos producidos por una carga rectangular como pudiera ser la de una losa de cimentación o la de una zapata. Estos asientos pueden producirse instantáneamente o bien con el paso del tiempo, los llamados asientos de consolidación. El modelo elástico proporciona soluciones para una gran variedad de problemas, y si bien el comportamiento del terreno no es generalmente elástico, hoy día se dispone de una amplia experiencia respecto al uso y limitaciones.
Una de las grandes ventajas que presenta la hipótesis de que el terreno es elástico lineal es la validez del principio de superposición, cuyo enunciado dice que “si se tienen dos estados de tensiones y deformaciones correspondientes, al estado tensional suma le corresponde el estado de deformaciones suma“.
Para el cálculo de las deformaciones con la teoría elástica es necesario conocer el módulo de elasticidad o módulo de Young, E, así como el coeficiente de Poisson, γ. Sin embargo, según el Principio de Terzaghi, “las deformaciones en suelos se deben a la variación de las tensiones efectivas“, por lo que las ecuaciones de Hooke deben escribirse en términos efectivos. Es decir, se deben utilizar E‘ y γ‘, obtenidos en condiciones drenadas del suelo, es decir, a largo plazo. Este método sería válido para cargas de servicio o de trabajo, alejadas de la carga de rotura (factor de seguridad del orden de 3), que probablemente generen asientos elásticos. El método elástico será tanto más aceptable cuanto más se asemeje el comportamiento del suelo al del sólido lineal-elástico, como es el caso de los suelos granulares o las arcillas fuertemente sobreconsolidadas, bajo presiones normales de cimentación.
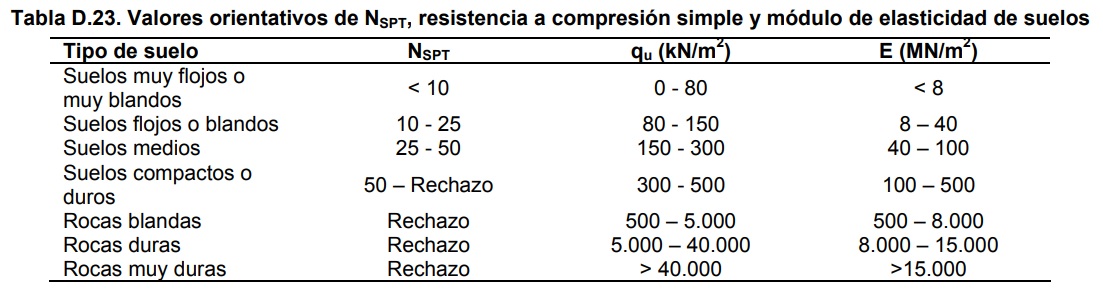
En las Tablas D.23 y D.24 del Código Técnico de Edificación se recogen valores orientativos de los módulos de elasticidad E‘ y del coeficiente de Poisson γ‘. En algunos casos no es posible trabajar con tensiones efectivas, por lo que en Geotecnia se hace en totales, utilizando unos parámetros elásticos en totales o aparentes.
Como un suelo saturado responde a corto plazo sin variar su volumen, ello supone un coeficiente de Poisson de 0,5 trabajando en tensiones totales. En ese caso se utiliza un módulo de elasticidad Eu denominado “módulo de elasticidad sin drenaje“. Este módulo es de difícil determinación, aunque se suele considerar Eu = 500·Cu, pero con errores del orden del 50%. Skempton recomienda adoptar como Eu el módulo secante correspondiente a una tensión aplicada igual al 65% de la tensión de rotura (coeficiente de seguridad F=3 en cimentaciones superficiales). Como los esfuerzos cortantes son iguales en tensiones totales o en efectivas, los módulos de rigidez G coincidirán, lo cual permite deducir Eu conocidos E‘ y γ‘ con la siguiente expresión:
Llegado a este punto, ¿cómo calculamos las deformaciones verticales al aplicar una carga sobre el terreno? Llamaremos “asientos” a dicha deformación vertical, distinguiéndose los “asientos instantáneos” los que ocurren a corto plazo, es decir, en condiciones sin drenaje. A ellos habría que sumar los asientos a largo plazo, en condiciones de drenaje, que son los “asientos de consolidación“. Por tanto, los asientos totales se calcularán con E‘ y γ‘ (condiciones drenadas, a largo plazo) y los asientos instantáneos con Eu y con γ = 0,5. La diferencia serán los asientos diferidos (semejantes a los de consolidación). Veamos ahora los cálculos.
Para cargas flexibles con forma circular, cuadrada o rectangular, el asiento bajo el centro de las mismas se obtiene con la siguiente expresión:
En la que B es el lado menor del área cargada y IS es un coeficiente de influencia que vale IS =1 en cargas circulares y IS =1,122 en cargas cuadradas. Para cargas rectangulares se puede obtener el asiento en una esquina con la fórmula anterior pero adoptando un coeficiente de influencia que viene dado por esta expresión, donde n=L/B:
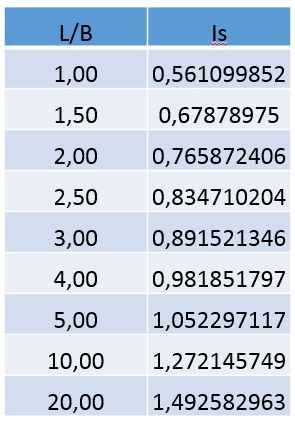
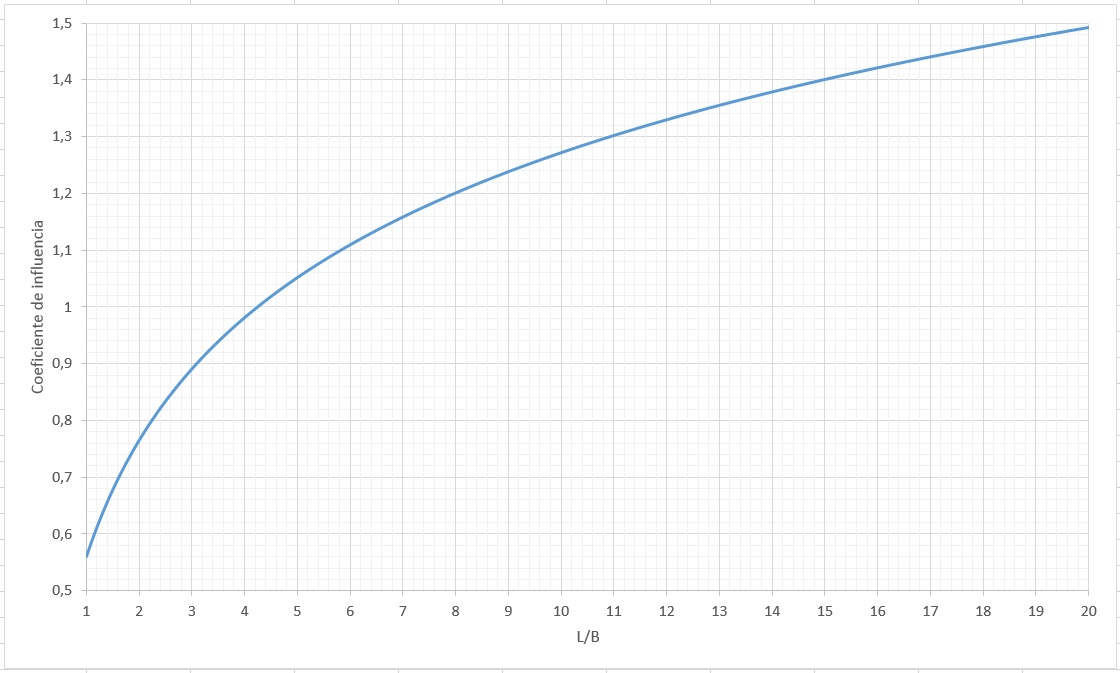
El Cuadro 1 y la Figura 1 nos dan valores para este coeficiente de influencia.
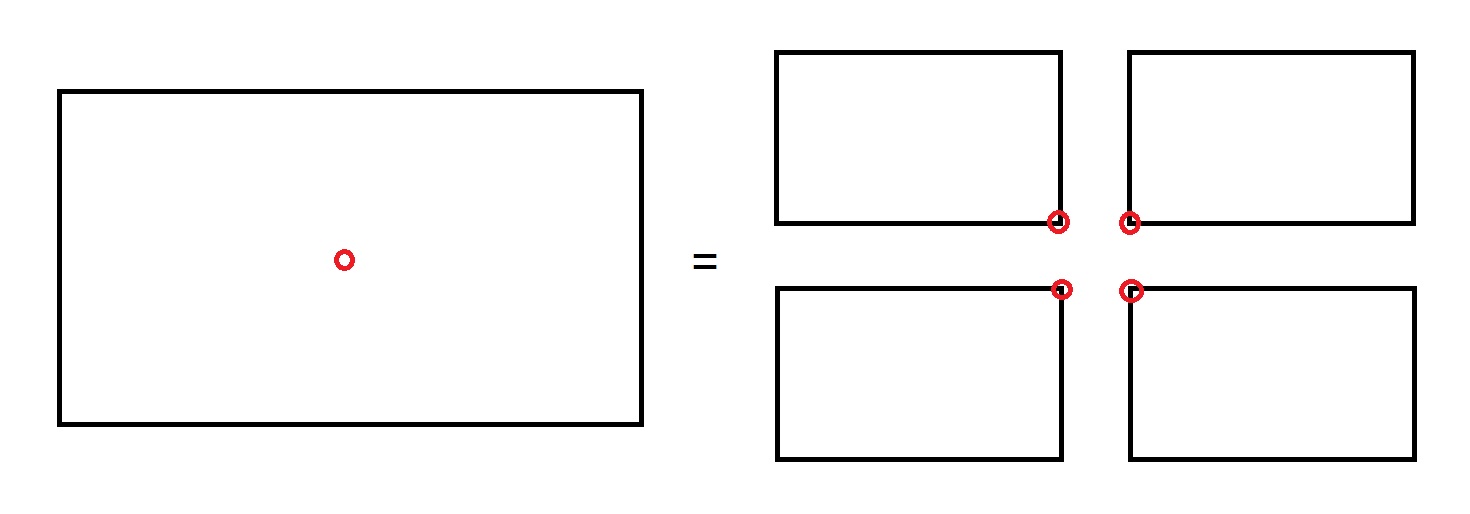
Aplicando el principio de superposición que permite la teoría elástica, el lector puede comprobar de forma sencilla que el asiento en el centro es el doble que en una de sus esquinas (Figura 2).
Por último, en el caso de una carga rígida, como sería el caso de muchas zapatas, se considera que el asiento es uniforme e igual, aproximadamente, a 0,8 veces el asiento que se obtendría en el centro si fuese una zapata flexible. Es fácil comprobar que dicho asiento valdría.
Como recordatorio, habría que decir que la carga que se aplica en superficie en las fórmulas anteriores se debería cambiar por la carga o tensión neta en el caso de que la carga se aplique tras una excavación previa. Es decir, la carga a utilizar en las fórmulas es la diferencia entre la tensión aplicada en superficie y la existente en el terreno a la profundidad del plano de cimentación. Dicho de otra forma, hay que quitar de la carga total aplicada la correspondiente al peso del terreno excavado.
Se deja al lector inquieto calcular el asiento en el centro de una zapata rectangular de 2,50 m x 5,00 m que se cimenta sobre unas arcillas con un peso específico saturado de 22 kN/m3, con un módulo de elasticidad efectivo de 92,00 MPa y un coeficiente de Poisson efectivo de 0,5. La zapata se apoya a 2,00 m de profundidad y el peso propio que se le transmite es de 100 kN/m2.
Referencias:
- DAS, B. (2005). Fundamental of Geotechnical Engineering – 2nd ed, Technomic Publishing Co.
- GONZÁLEZ CABALLERO, M. (2001). El terreno. Edicions UPC, 309 pp.
- GONZÁLEZ DE VALLEJO, L.I. et al. (2004). Ingeniería Geológica. Pearson, Prentice Hall, Madrid.
- IZQUIERDO, F.A. (2001). Cuestiones de geotecnia y cimientos. Editorial Universidad Politécnica de Valencia, 227 pp.
- YEPES, V. (2020). Procedimientos de construcción de cimentaciones y estructuras de contención. Colección Manual de Referencia, 2ª edición. Editorial Universitat Politècnica de València, 480 pp. Ref. 328. ISBN: 978-84-9048-903-1.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.