Recuerdo los quebraderos de cabeza que teníamos en mis primeras obras de carreteras cuando teníamos que aceptar determinadas zahorras por culpa del equivalente de arena. Se trata de un ensayo, muy sencillo en cuanto a su realización, que permite estimar la cantidad de finos presentes en un suelo poco plástico o en un árido fino. Este ensayo lo propuso F.N. Hveem para evaluar cualitativamente, de forma rápida, la cantidad y la actividad de los finos de un suelo. En apretada síntesis, se trata de evaluar la limpieza de un material que llega a una obra para utilizarlo como base granular, relleno drenante o incluso, en el caso de arenas, para su uso en hormigones o en aglomerados. Lo que se busca es un equivalente de arena alto, pues cuanto mayor es este valor, más alta sería la calidad del material.
Para realizar este ensayo debemos acudir a la norma UNE-EN 933-8: “Ensayos para determinar las propiedades de los áridos. Parte 8: Evaluación de los finos. Ensayo del equivalente de arena”. También se puede recurrir a otras normas como la ASTM D2429. Este ensayo se aplica a la fracción arenosa de un suelo. Tras mezclar el suelo seco con un líquido floculante de la arcilla, se agita la mezcla y se deja reposar durante un tiempo para medir la altura que alcanza la parte arcillosa y la que tiene la parte arenosa. Para eso se utiliza una varilla especial. El Equivalente de Arena (EA) sería la relación entre la altura de la arena respecto a la altura de la arcilla multiplicada por 100, tal y como podemos ver en la Figura 1.
En este enlace la Escuela de Ingenieros de Caminos de Madrid tenéis una descripción del ensayo y unos vídeos explicativos que creo os pueden interesar: http://www2.caminos.upm.es/departamentos/ict/lcweb/ensayos_aridos/equivalente_arena.html
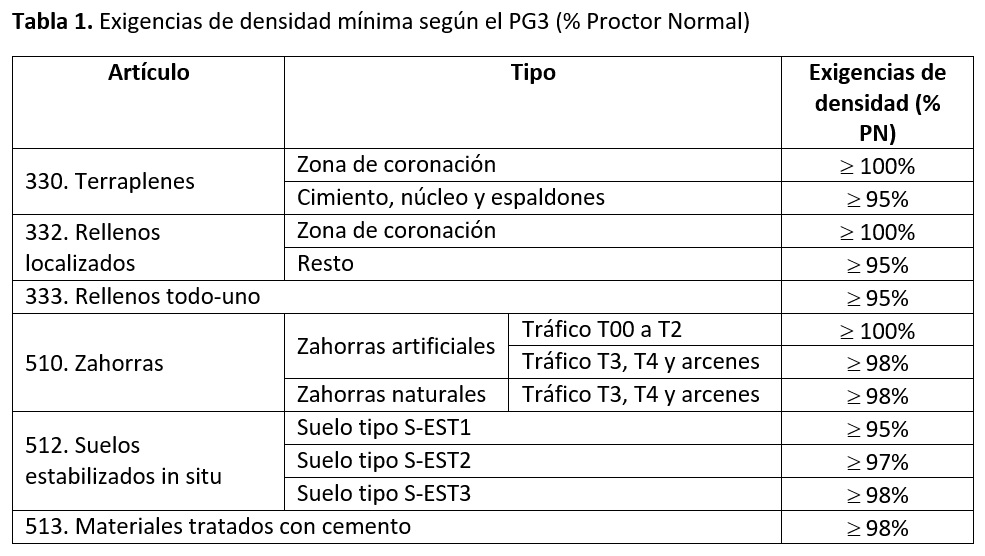
El Equivalente de Arena es un ensayo que puede poner en entredicho la calidad de un material usado en carreteras, tal y como os comenté en el caso de mis primeras obras en el entorno de Valencia. Así, por ejemplo, para una zahorra artificial el PG-3 exige un valor superior a 40 cuando se trata de un tráfico T00 a T1, mismo valor que el usado para el material usado para un gravacemento tipo GC20 o un riego de imprimación o curado. Para las mezclas bituminosas en caliente ya se exige un valor de 55 y en el caso de pavimentos de hormigón en zonas sometidas a heladas, el EA debe superar 80.
En el caso del hormigón estructural, el reciente “Código estructural” de 2021 indica que el EA no será inferior a 70 en el caso de hormigones usados en obras sometidas a la clase de exposición X0 o XC, mientras que será de 75 en el resto de los casos. No obstante, si las arenas proceden del machaqueo de rocas calizas o dolomías (rocas sedimentarias carbonáticas que contienen al menos un 70% de calcita, dolomita o de ambas) que no cumplan con el equivalente de arena, pueden aceptarse como válidas bajo determinadas condiciones usando el ensayo azul de metileno, según la norma UNE-EN 933-9.
Las decisiones que se toman con este ensayo son de gran calado. Podemos rechazar un material que sea el que tengamos a nuestra disposición, siendo inviable económicamente traer otro material alternativo. Por tanto, es procedente revisar la exactitud que tiene el ensayo.
En efecto, este ensayo debe tomarse como un control rápido que sustituya a un ensayo granulométrico, pues los resultados se encuentran muy influenciados por las características del fino presente (por ejemplo, si son limos o arcillas). Incluso si se trata de una arcilla, la composición mineralógica y su reacción al líquido floculante pueden influir en los resultados. No es lo mismo un fino calizo que otro silíceo, o una arcilla muy plástica o expansiva.
Por otra parte, si se realiza la agitación por parte de una persona que no siga escrupulosamente las instrucciones del ensayo, se pueden incrementar los errores. Por lo que se prefiere siempre una agitación mecánica normalizada.
Dicho esto, la recomendación es evidente. Cuando un material va sobrado en cuanto a su Equivalente de Arena, este ensayo rápido supone un control para evitar contaminación o problemas puntuales de calidad. Pero si estamos en una situación límite, lo que hay que hacer es buscar la correlación entre el Equivalente de Arena y el Ensayo Granulométrico para corregir las desviaciones que pudiesen haber. Siempre mandará el Ensayo Granulométrico en caso de duda.
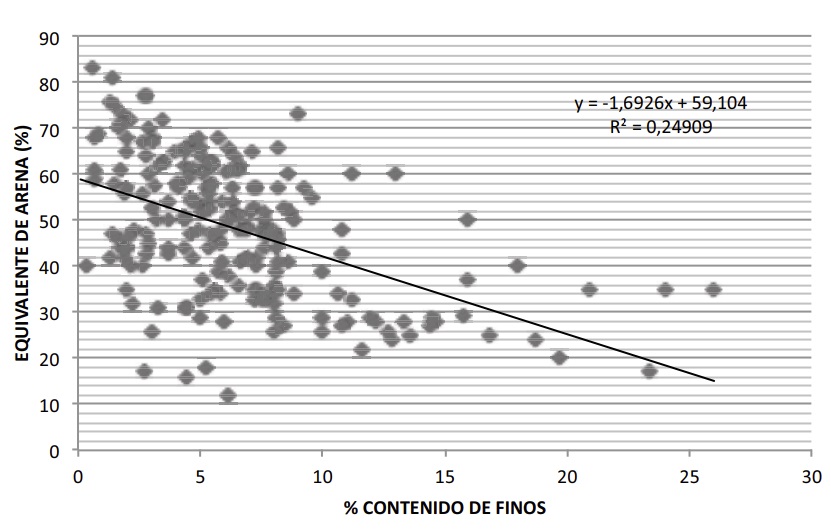
En la Figura 2 se observa que, si bien hay cierta tendencia a que el menor contenido de finos tiende a presentar más altos de equivalente de arena, el coeficiente de determinación de dicha relación es bajo (el modelo explica algo menos del 25% de la variabilidad). No obstante, si el material tiene la misma procedencia, la variabilidad es mucho menor que en el caso de materiales diferentes. Sea como sea, no podemos rechazar directamente un material con un EA bajo sin tomar las precauciones debidas.
Os dejo a continuación un vídeo donde se explica el ensayo del Equivalente de Arena.
Referencias:
ANEFA (2018). Guía española de áridos reciclados procedentes de residuos de construcción y demolición (RCD), 292 pp.
Morilla, I. (2012). Interpretación de los ensayos geotécnicos en suelos. 627 pp., Madrid.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.