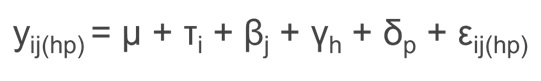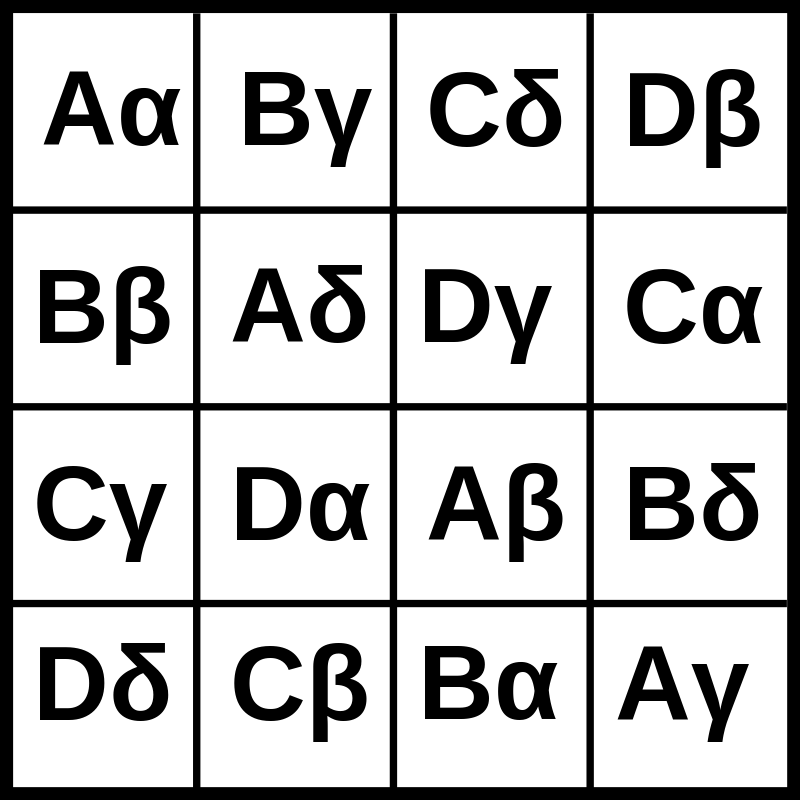
Un cuadrado greco-latino, cuadrado de Euler o cuadrados latinos ortogonales de orden n se denomina, en matemáticas, a la disposición en una cuadrícula cuadrada n×n de los elementos de dos conjuntos S y T, ambos con n elementos, cada celda conteniendo un par ordenado (s, t), siendo s elemento de S y t de T, de forma que cada elemento de S y cada elemento de T aparezca exactamente una vez en cada fila y en cada columna y que no haya dos celdas conteniendo el mismo par ordenado. Si bien los cuadrados grecolatinos eran una curiosidad matemática, a mediados del siglo XX Fisher demostró su utilidad para el control de experimentos estadísticos.
El diseño de experimentos en cuadrado grecolatino constituye una extensión del cuadrado latino. En este caso se eliminan tres fuentes extrañas de variabilidad, es decir, se controlan tres factores de bloques y un factor de tratamiento. Se trata de un diseño basado en una matriz de “n” letras latinas y “n” letras griegas, de forma que cada letra latina aparece solo una vez al lado de cada letra griega. Lo interesante de este diseño es que se permite la investigación de cuatro factores (filas, columnas, letras latinas y letras griegas), cada una con “n” niveles en solo “n2” corridas. Se llama cuadrado grecolatino porque los cuatro factores involucrados se prueban en la misma cantidad de niveles, de aquí que se pueda escribir como un cuadro. En la Figura 1 se presenta el aspecto de los datos del diseño de orden cuatro. El inconveniente de este modelo es que su utilización es muy restrictiva. El análisis de la varianza permite comprobar las hipótesis de igualdad de letras latinas (tratamientos), de las filas, de las columnas y de las letras griegas.
Si a un cuadrado latino p x p se le superpone un segundo cuadrado latino n x n en el que los tratamientos se denotan con letras griegas, entonces los dos cuadrados tienen la propiedad de que cada letra griega aparece una y sólo una vez con cada letra latina. Este diseño permite controlar sistemáticamente tres fuentes de variabilidad extraña. Ello permite la investigación de cuatro factores (filas, columnas, letras latinas y letras griegas), cada una con p niveles en sólo n2 ensayos.
Por tanto, el diseño de experimentos en cuadrado grecolatino se caracteriza por lo siguiente:
- Es un diseño con cuatro factores a n niveles
- Se asume que no hay interacciones entre los factores
- Requiere de n2 observaciones
- Cada nivel de un factor aparece una vez con cada nivel de los otros factores
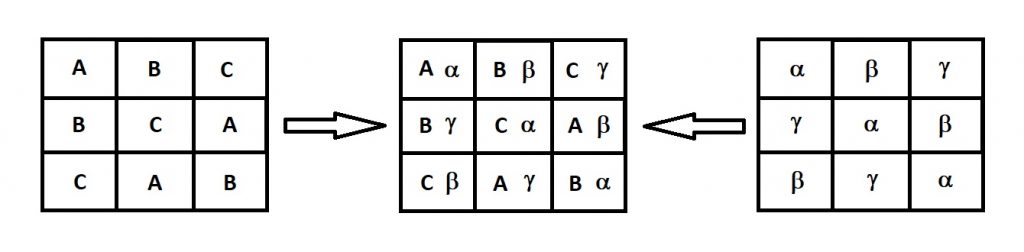
- Se trata de la superposición de dos cuadrados latinos (ver Figura 2)
En un diseño en cuadrado greco-latino la variable respuesta yij(hp) viene descrita por la siguiente ecuación:
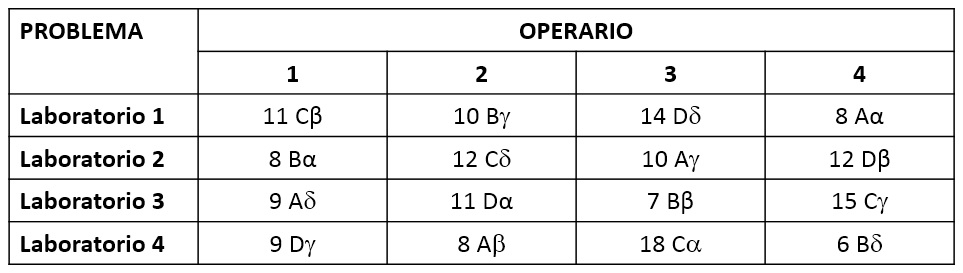
A continuación os presento un caso para aclarar la aplicabilidad de este diseño de experimentos. Se trata de averiguar si la resistencia característica del hormigón a flexocompresión (MPa) varía con cuatro dosificaciones diferentes. Para ello se han preparado amasadas en cuatro amasadoras diferentes, se han utilizado cuatro operarios de amasadora y los ensayos se han realizado en cuatro laboratorios diferentes. Los resultados se encuentran en la tabla que sigue. Se quiere analizar el diseño de experimentos en cuadrado grecolatino realizado.
En el caso que nos ocupa, la variable de respuesta de la resistencia característica del hormigón a flexocompresión (MPa). El factor que se quiere estudiar es la dosificación a cuatro niveles (A, B, C y D). El bloque I es el tipo de amasadora, con cuatro niveles (α, β, γ y δ). El bloque II es el operario de la amasadora, con cuatro niveles (1, 2, 3 y 4). El bloque III es el laboratorio, con cuatro niveles (las filas). Se supone que no hay interacción entre el factor y los bloques entre sí.
Lo que se quiere averiguar es si hay diferencias significativas entre las dosificaciones (el factor a estudiar). De paso, se desea saber si hay diferencias entre los laboratorios, los operarios y las amasadoras (los bloques).
Os paso un pequeño vídeo donde se explica, de forma muy resumida, este caso, tanto para SPSS como para MINITAB.
Os dejo otro vídeo donde también se explica este tipo de diseño de experimentos.
Referencias:
- Gutiérrez, H.; de la Vara, R. (2004). Análisis y Diseño de Experimentos. McGraw Hill, México.
- Vicente, MªL.; Girón, P.; Nieto, C.; Pérez, T. (2005). Diseño de Experimentos. Soluciones con SAS y SPSS. Pearson, Prentice Hall, Madrid.
- Pérez, C. (2013). Diseño de Experimentos. Técnicas y Herramientas. Garceta Grupo Editorial, Madrid.