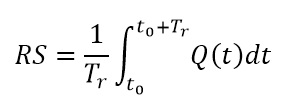La resiliencia es un concepto que viene del mundo de la psicología y representa la capacidad para adaptarse de forma positiva frente a situaciones adversas. Proviene del latín resilio, «volver atrás, volver de un salto, resaltar, rebotar». En el campo de la mecánica, la resiliencia sería la capacidad de un material para recuperar su forma inicial después de haber sido deformado por una fuerza. En la ecología, un sistema es resiliente si puede tolerar una perturbación sin colapsar a un estado completamente distinto, controlado por otro conjunto de procesos. En un entorno tecnológico, este término se relaciona con la capacidad de un sistema de soportar y recuperarse ante desastres y perturbaciones. En este artículo vamos a indagar en el concepto de resiliencia de las infraestructuras.
Así, dentro de los objetivos de desarrollo sostenible de Naciones Unidas (Figura 1), encontramos el Objetivo 9: Construir infraestructuras resilientes, provomer la industrialización sostenible y fomentar la innovación. En efecto, las infraestructuras deben hacer frente al crecimiento de la población, pero también a los crecientes peligros físicos (cinéticos) como el terrorismo, o los asociados al clima extremo y los desastres naturales. La frecuencia y gravedad de estos eventos extremos se prevén crecientes, y, por tanto, es más que previsible un aumento en los costes e impacto humano. Además, debido a la cada vez más informatización y digitalización de las infraestructuras, el riesgo de ataques informáticos a las infraestructuras es más que evidente.
La resiliencia puede asociarse con cuatro atributos: robustez, que es la capacidad para resistir un evento extremo sin que el fracaso en la funcionalidad sea completo; rapidez, que sería la capacidad de recuperarse de forma eficiente y efectiva; la redundancia, que sería la reserva de componentes o de sistemas estructurales sustitutivos; y el ingenio, que sería la eficiencia en la identificación de problemas, priorizando soluciones y movilizando recursos para su solución (Bruneau et al., 2003).
Matemáticamente, se puede evaluar la resiliencia integrando la curva de funcionalidad a lo largo del tiempo (ver Figura 2).
donde Q(t) es la funcionalidad; t0 es el momento en el que ocurre el evento extremo y Tr es el horizonte hasta donde se estudia la funcionalidad.
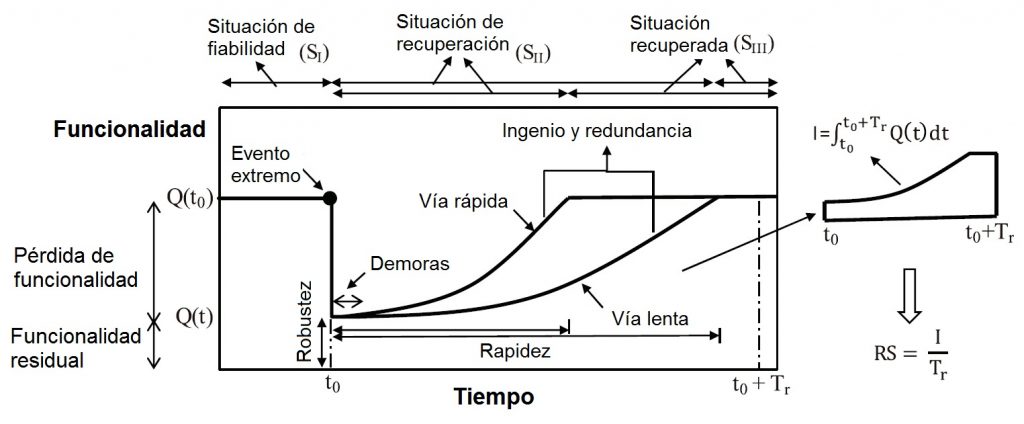
En la Figura 2 se pueden observar los tres estados correspondientes con la funcionalidad. En la situación de fiabilidad, la infraestructura se encuentra con la funcionalidad de referencia, previo al evento extremo. La situación de recuperación comienza tras la ocurrencia del evento extremo, con una pérdida de funcionalidad dependiente de la robustez de la infraestructura, y con una recuperación que depende de los esfuerzos realizados en la reparación, que puede ser rápida o lenta en función del ingenio o la creatividad en las soluciones propuestas, así como de la redundancia de los sistemas previstos. Por último, la situación recuperada es la que ocurre cuando la funcionalidad vuelve a ser la de referencia.
Se comprueba en la Figura 2 cómo una infraestructura pasa de una funcionalidad de referencia a una residual tras el evento extremo. Tras el evento, puede darse una demora en la recuperación de la funcionalidad debido a las tareas de inspección, rediseño, financiación, contratación, permisos, etc.). La recuperación completa de la funcionalidad depende de la forma en la que se han abordado las tareas de reparación. Es fácil verificar que la resiliencia se puede calcular integrando la curva de recuperación de la funcionalidad desde la ocurrencia del evento extremo hasta la completa recuperación, dividiendo dicho valor por el tiempo empleado en dicha recuperación.
Este modelo simplificado permite establecer las pautas para mejorar la resiliencia de una infraestructura:
a) Incrementando la robustez de la infraestructura, es decir, maximizar su funcionalidad residual tras un evento extremo.
b) Acelerando las actividades de recuperación de la funcionalidad de la infraestructura.
En ambos casos, es necesario concebir la infraestructura desde el principio con diseños robustos, con sistemas redundantes y con una previsión de las tareas de reparación necesarias.
Con todo, la capacidad de recuperación comprende cuatro dimensiones interrelacionadas: técnica, organizativa, social y económica (Bruneau et al., 2003). La dimensión técnica de la resiliencia se refiere a la capacidad de los sistemas físicos (incluidos los componentes, sus interconexiones e interacciones, y los sistemas enteros) para funcionar a niveles aceptables o deseables cuando están sujetos a los eventos extremos. La dimensión organizativa de la resiliencia se refiere a la capacidad de las organizaciones que gestionan infraestructuras críticas y tienen la responsabilidad de tomar decisiones y adoptar medidas que contribuyan a lograr la resiliencia descrita anteriormente, es decir, que ayuden a lograr una mayor solidez, redundancia, ingenio y rapidez. La dimensión social de la resiliencia consiste en medidas específicamente diseñadas para disminuir los efectos de los eventos extremos por parte de la población debido a la pérdida de infraestructuras críticas. Análogamente, la dimensión económica de la resiliencia se refiere a la capacidad de reducir tanto las pérdidas directas e indirectas de los eventos extremos.
El problema de estas cuatro dimensiones se pueden sumar de forma homogénea, con interrelaciones entre ellas. El reto consiste en cuantificar y medir la resiliencia en todas sus dimensiones, así como sus interrelaciones. Se trata de un problema de investigación de gran trascendencia y complejidad, que afecta al ciclo de vida de las infraestructuras desde el inicio de la planificación (Salas y Yepes, 2020).
Referencias:
ANWAR, G.A.; DONG, Y.; ZHAI, C. (2020). Performance-based probabilistic framework for seismic risk, resilience, and sustainability assessment of reinforced concrete structures. Advances in Structural Engineering, 23(7):1454-1457.
BRUNEAU, M.; CHANG, S.E.; EGUCHI, R.T. et al. (2003). A framework to quantitatively assess and enhance the seismic resilience of communities. Earthquake Spectra 19(4): 733–752.
SALAS, J.; YEPES, V. (2020). Enhancing sustainability and resilience through multi-level infrastructure planning. International Journal of Environmental Research and Public Health, 17(3): 962. DOI:10.3390/ijerph17030962

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.