estadística archivos - El blog de Víctor Yepes

¿Es real o es solo azar? 5 revelaciones del ANOVA para dominar tus datos

Introducción: El dilema de las medias engañosas.

Imagine que supervisa a tres profesores con métodos pedagógicos diferentes o que analiza la viscosidad de cinco lotes de producción. Al revisar los resultados, observa que las medias no son iguales. Entonces surge la pregunta crítica que separa a un gestor de un estratega: ¿esta diferencia indica una verdadera oportunidad operativa o es simplemente ruido estadístico?

Actuar basándose en el «ruido» genera una ineficiencia operativa masiva: se podría detener una línea de producción sin necesidad o ignorar un fallo sistémico costoso simplemente por falta de rigor. Para resolver este dilema, la estadística nos ofrece la herramienta «detective» definitiva: el ANOVA (Análisis de Varianza), diseñado para determinar si las diferencias entre tres o más grupos son lo suficientemente significativas como para justificar una decisión empresarial.

¿Por qué la prueba t no es suficiente?

Para comparar dos niveles (por ejemplo, hombres frente a mujeres), la prueba t de Student es adecuada. Sin embargo, cuando enfrentamos tres o más grupos, el ANOVA es obligatorio por una razón técnica crucial: la inflación del error alfa.

Si intentáramos comparar múltiples pares usando pruebas t individuales (lote 1 frente a lote 2, lote 2 frente a lote 3 y lote 1 frente a lote 3), el riesgo de error se acumularía. Cada prueba individual tiene una probabilidad del 5 % de detectar una «falsa diferencia» (falso positivo). Al encadenar pruebas, ese riesgo del 5 % crece exponencialmente, lo que nos lleva a conclusiones erróneas. El ANOVA neutraliza este riesgo al analizar todos los grupos simultáneamente bajo una premisa fundamental:

Hipótesis nula (H₀): todas las medias poblacionales son iguales (H₀: μ₁ = μ₂ = ⋯ = μ_k). El punto de partida estratégico consiste en asumir que el factor estudiado no tiene influencia real hasta que la varianza demuestre lo contrario.

La paradoja central: comparar medias al analizar la variabilidad.

El concepto más contraintuitivo del ANOVA es que, para saber si las medias son distintas, no estudiamos las medias, sino la varianza. El análisis descompone la variabilidad total en dos fuentes:

Variación entre grupos (factor): el efecto real del tratamiento o de la variable (por ejemplo, el impacto de un nuevo fertilizante).
Variación dentro de los grupos (error): el ruido aleatorio o las diferencias que no pueden explicarse por el azar.

Un estratega sénior no solo busca diferencias, sino que también cuantifica la variabilidad explicada. Usando la relación (SCE/SCT) × 100, podemos determinar qué porcentaje del «caos» de los datos corresponde a la responsabilidad directa del factor analizado. Si el lote explica, por ejemplo, el 44,95 % de la variación de la viscosidad, se trata de un hallazgo de alto impacto administrativo.

El valor p y la razón F: tu seguro contra la casualidad.

Si el ANOVA es un detective, la razón F es su lupa. Matemáticamente, es la relación entre la media de los cuadrados del factor y la media de los cuadrados del error (MC_Factor/MC_Error). Si la razón F es significativamente mayor que 1, la «señal» del factor es más fuerte que el «ruido» del azar.

Esta potencia se traduce en el valor p, que es nuestra medida de riesgo. Consideremos el caso del gel adhesivo: tras las quejas de los clientes, se analizaron cinco lotes. El lote 3 mostró una media de 26,77, notablemente inferior al estándar de 30. El ANOVA arrojó un valor p de 0,0012, lo que constituye una prueba contundente para que la gerencia intervenga específicamente en ese lote.

Definición del valor p: probabilidad de observar una varianza en las medias muestrales por mero azar. Un valor p inferior a 0,05 indica que el riesgo de que se trate de un espejismo es lo suficientemente bajo como para actuar.

El ANOVA no es una brújula, sino una alarma.

Es un error común creer que el ANOVA señala al «culpable». En realidad, el ANOVA funciona como una alarma: confirma que «no todas las medias son iguales», pero no especifica cuál es la diferente.

Una vez que suena la alarma (p < 0,05), el estratega debe utilizar una «brújula»: las pruebas de comparación múltiple. Herramientas como la prueba de Tukey-Kramer o la HSD de Tukey permiten comparar pares de grupos para identificar exactamente dónde se encuentra la anomalía y realizar una inversión de recursos quirúrgicos de manera eficiente.

Resiliencia estadística: qué hacer cuando las reglas se rompen.

Para que un ANOVA tradicional sea fiable, los datos deben ser normales y presentar homocedasticidad, es decir, igualdad de varianzas. La prueba de Levene es el filtro crítico aquí.

Si el valor p de Levene es mayor que 0,05, las varianzas son iguales y el ANOVA es el camino seguro.
Si Levene es significativo (p < 0,05), las reglas se han roto y el ANOVA estándar pierde validez.

En este escenario de crisis de datos, el investigador recurre a la prueba de Welch. Se trata de una alternativa robusta que permite comparar medias con precisión, incluso cuando las varianzas son desiguales, y que preserva la investigación sin sacrificar el rigor científico.

Conclusión: del dato a la decisión inteligente.

El ANOVA transforma los datos brutos en pruebas de la influencia. Ya sea para validar si un medicamento reduce el tiempo de curación o si un cambio en la composición del hormigón aumenta su resistencia, esta técnica nos permite distinguir entre casualidad y causalidad.

En última instancia, la excelencia en la gestión no consiste en promedios simples, sino en comprender qué parte de los resultados se debe a la variabilidad explicada por las decisiones adoptadas y qué parte es ruido.

Reflexione sobre su operación de hoy: ¿qué variaciones observa en sus procesos que podrían validarse —o descartarse— mediante el rigor del ANOVA?

En esta conversación puedes escuchar algunas de las ideas más importantes sobre ANOVA.

Este vídeo resume bien el tema.

One_Way_ANOVA_Mastery

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

La magia de la síntesis: cómo ordenar el caos de tus datos

Introducción: El dilema del exceso de información.

Imagine que se encuentra frente a una base de datos con cientos de columnas que detallan cada aspecto de su actividad. A primera vista, parece un tesoro, pero en la práctica, tener «demasiada» información a menudo paraliza la toma de decisiones. El ruido de los datos irrelevantes y la redundancia de variables que dicen esencialmente lo mismo ocultan las tendencias estratégicas reales.

Es aquí donde el análisis de componentes principales (PCA) resulta indispensable. Más que una técnica estadística de análisis multivariante, el PCA actúa como un «traductor inteligente» que simplifica la complejidad. Su función es transformar el caos de variables correlacionadas en un conjunto claro de factores que revelan la estructura real de su negocio.

Punto 1: Menos es más (la simplificación inteligente).

La esencia del PCA radica en la reducción de la dimensionalidad. En lugar de intentar procesar 20 variables que fluctúan juntas, esta técnica las sintetiza en un nuevo subconjunto de «factores» independientes.

Simplificar no implica pérdida de información. En el mundo del análisis de datos, simplificar significa ganar claridad. Al eliminar la redundancia, el PCA nos permite centrarnos en las fuerzas subyacentes que realmente marcan la diferencia. Como establece un principio fundamental del análisis multivariante:

«El exceso de variables dificulta el análisis de la información y genera redundancia; el PCA examina la interdependencia para reducir la dimensión a variables no observables».

Punto 2: La regla del 80 %. ¿Cuándo es «suficiente» información?

Para un estratega de datos, el rigor matemático debe equilibrarse con la utilidad práctica. ¿Cuánta información debemos conservar para que el modelo refleje fielmente la realidad? Las fuentes técnicas dictan criterios claros basados en la varianza explicada acumulada:

El mínimo académico: en ciertos contextos, explicar el 60 % de la varianza constituye el umbral básico aceptable.
Propósitos descriptivos: para entender las tendencias generales, suele bastar con alcanzar el 80 %.
Análisis predictivos: si los componentes se integran en modelos de machine learning posteriores, se recomienda capturar al menos el 90 %.
Criterio de Kaiser: establece que, para ser eficientes, solo se deben conservar los componentes con autovalores superiores a 1. Si un componente no explica más variación que una sola variable original, se trata de ruido estratégico y debe descartarse.

Punto 3: descubriendo variables «invisibles».

El PCA puede revelar estructuras que no existen en ninguna columna específica, pero que rigen el sistema. Para descubrir estas estructuras «invisibles», primero debemos decidir matemáticamente dónde termina la señal y dónde empieza el ruido.

Veamos dos ejemplos del mundo real presentes en los materiales de análisis:

Estabilidad financiera: al analizar variables como ingresos, educación, edad, empleo y ahorros, el PCA permite agruparlas en una dimensión principal denominada «estabilidad financiera a largo plazo». Asimismo, las deudas y las tarjetas de crédito pueden consolidarse en un factor denominado «historial crediticio».
Ingeniería de puentes: En un estudio de 61 puentes de losa, variables técnicas como la luz principal y el canto del tablero se fusionan matemáticamente para definir la «proporción geométrica» de la estructura, mientras que la armadura activa y el hormigón definen su «capacidad estructural».

El PCA nos permite dejar de ver filas de números y empezar a ver conceptos abstractos y accionables.

Punto 4: Gráfico de sedimentación. La «luz» en el camino.

Para evitar la subjetividad, el analista confía en el gráfico de sedimentación. Esta herramienta visual ordena los autovalores de mayor a menor y muestra una caída que finalmente se estabiliza.

La clave está en identificar el «punto de inflexión» o el «codo» de la gráfica. Los componentes que se encuentran en la pendiente pronunciada, antes de que la curva se transforme en una línea plana (la zona de sedimentación), son los que contienen la esencia de los datos. Este método garantiza que la reducción se base en la evidencia y no en la intuición.

Punto 5: El «giro» necesario (la potencia de la rotación).

Un resultado inicial de PCA puede ser técnicamente correcto, pero «estratégicamente inútil» si las variables originales tienen pesos similares en varios componentes. Es como mirar una imagen desenfocada.

La solución es la rotación (específicamente, el método Varimax con normalización de Kaiser). Este ajuste matemático redistribuye las cargas para que cada variable original se asocie claramente a un único factor. La rotación no altera la información, sino que «ajusta la lente» para que la interpretación de cada dimensión sea nítida, lo que permite a los interesados comprender exactamente qué significa cada componente.

Punto 6: Rigor técnico y tamaño de la muestra.

El PCA no es un acto de magia, sino que requiere cimientos sólidos. La efectividad de la técnica depende de la presencia de correlaciones significativas (superiores a 0,3) y de contar con una muestra representativa. Desde el punto de vista académico, se exige un mínimo de 5 observaciones por variable, aunque el ratio óptimo es de 10 a 1.

Además, la validez de una carga factorial depende directamente del tamaño de la muestra, como se detalla en la siguiente escala de rigor:

Tamaño de la muestra	Carga factorial mínima requerida
350 observaciones	0,30
200 observaciones	0,40
150 observaciones	0,45
120 observaciones	0,50
100 observaciones	0,55
85 observaciones	0,60
70 observaciones	0,65
60 observaciones	0,70
50 observaciones	0,75

Un paso crítico final es el análisis de las comunalidades. Si una variable tiene una comunalidad inferior a 0,5, significa que el modelo no logra explicar su varianza de manera satisfactoria. En términos estratégicos, esa variable se considera «carente de explicación» y debería eliminarse para no contaminar el análisis.

Conclusión: mirando al futuro de tus datos.

El análisis de componentes principales es una pieza angular de la preparación de datos. Al eliminar el ruido, preparamos el terreno para técnicas avanzadas de aprendizaje automático, como el agrupamiento o la predicción, que funcionan con mayor agilidad sobre datos sintetizados.

En un mercado saturado de información, la ventaja competitiva pertenece a quienes logran destilar el conocimiento. ¿Cómo cambiaría su visión estratégica si pudiera reducir sus 100 indicadores de rendimiento a solo tres dimensiones maestras que realmente explicaran el éxito de su organización?

Este vídeo puede servirles para introducir las ideas más importantes.

En esta conversación puedes escuchar las ideas más interesantes sobre este tema.

El vídeo sintetiza bien lo más importante del análisis de componentes principales.

PCA_Strategic_Clarity

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

El arte de predecir lo invisible: claves para entender la inferencia estadística

¿Cómo podemos determinar la intención de voto de toda una nación o evaluar la eficacia de un nuevo fármaco sin entrevistar a todos los ciudadanos ni tratar a todos los pacientes del planeta? En nuestra vida cotidiana, nos enfrentamos constantemente al reto de tomar decisiones globales basadas en información limitada. Medir el total de elementos suele ser física o económicamente inviable.

Como expertos en comunicación de datos, consideramos la inferencia estadística como el puente intelectual definitivo. Es la disciplina que nos permite pasar de lo que vemos —una pequeña muestra— a la realidad oculta de la población total. En esencia, es la herramienta científica que transforma la observación de unos pocos en el conocimiento preciso de la mayoría.

Población frente a muestra: la ventana hacia la verdad

Para descifrar la realidad, primero debemos distinguir entre los dos protagonistas del análisis: la población y la muestra. La población es el conjunto total que deseamos estudiar y la muestra es un subconjunto extraído de forma aleatoria que nos sirve de ventana para observar la población.

En este proceso, manejamos conceptos que debemos diferenciar con rigor:

Parámetro: Es el número «secreto» que describe la población. En la práctica, su valor es desconocido porque no podemos examinar a cada individuo. Usamos símbolos como la media poblacional (μ), la desviación típica (σ), la varianza (σ²) o el porcentaje o la proporción poblacional (p).
Estadístico: Es el número que calculamos directamente a partir de los datos muestrales. En este ámbito operamos con la media muestral, la desviación típica muestral, la varianza o la proporción muestral.

Dado que no podemos conocer el parámetro real, nos vemos obligados a operar en el mundo de los estadísticos para realizar estimaciones. El objetivo es claro:

«Extraer conclusiones sobre una población a partir de los datos de una muestra».

El intervalo de confianza: ¿qué tan cerca estamos de la realidad?

Dado que trabajar con muestras implica un error aleatorio inevitable, la estadística no ofrece un único número como verdad absoluta. En su lugar, construimos un intervalo de confianza de nivel C.

Conceptualmente, este rango se define mediante una estructura lógica: estimación ± error de la estimación.

No proporcionamos un único valor porque, en la práctica, el parámetro no se conoce. Por ello, el nivel de confianza C no es solo un porcentaje, sino la respuesta a una pregunta vital sobre la fiabilidad de nuestro trabajo: «¿Con qué frecuencia daría una respuesta correcta este método si lo utilizara muchas veces?». Si afirmamos que tenemos un 95 % de confianza, estamos diciendo que, si repitiéramos el muestreo el 95 % de las veces, nuestro intervalo contendría el verdadero valor del parámetro.

Inocente hasta que se demuestre lo contrario: la hipótesis nula (H0)

Como expertos, empleamos el contraste de hipótesis para evaluar si la evidencia de la muestra es suficiente para inferir una condición en toda la población. Este mecanismo examina dos afirmaciones opuestas:

La hipótesis nula (H0) representa el estado «habitual» o lo que cabría esperar si no hubiera cambios. Es una afirmación de «ausencia de efecto» o de «no diferencia». Algunos ejemplos críticos de H₀ son:

El acusado no es culpable (es inocente).
No hay embarazo.
No hay presencia de cáncer.

Para decidir si rechazamos la hipótesis nula, calculamos el p-valor (o significación muestral). A diferencia de lo que se cree popularmente, el p-valor no es un corte arbitrario, sino la probabilidad de obtener nuestros resultados si la hipótesis nula fuera cierta. Comparamos este p-valor con el nivel de significación (α), que es el límite preestablecido. Si p ≤ α, la evidencia es tan fuerte que rechazamos la situación «habitual» en favor de la hipótesis alternativa.

El dilema del error: falsos positivos y falsos negativos

En cualquier prueba estadística, asumimos el riesgo de tomar una decisión equivocada. Estos errores se dividen en dos categorías fundamentales:

Error tipo I (α): el «falso positivo» o riesgo del fabricante. Ocurre cuando rechazamos la hipótesis nula cuando esta es verdadera (por ejemplo, operar a una persona sana o condenar a un inocente).
Error tipo II (β): el «falso negativo». Sucede cuando aceptamos la hipótesis nula cuando es falsa (por ejemplo, declarar inocente a un asesino o no detectar una enfermedad).

Para minimizar estos riesgos, no solo tenemos en cuenta el nivel de significación (típicamente fijado en el 5 %), sino que también buscamos maximizar la potencia de la prueba (1 – β). Esta potencia representa nuestra capacidad para detectar un efecto cuando realmente existe y depende directamente del tamaño de la muestra y del nivel de significación. Decimos que un resultado tiene significación estadística cuando es tan improbable que no puede atribuirse razonablemente al azar (p ≤ α).

Propiedades del buen estimador

Para que nuestras conclusiones sean robustas, los métodos que utilizamos deben poseer cuatro pilares técnicos extraídos de la teoría de la probabilidad:

Sesgo: el estimador debe carecer de desviaciones sistemáticas; su media debe coincidir con el parámetro real.
Eficiencia: buscamos la menor variabilidad posible en los resultados.
Convergencia y consistencia: estas propiedades garantizan la fiabilidad del método a largo plazo.

La lógica matemática que hay detrás de la eficiencia es poderosa: si aumenta el tamaño de la muestra, disminuye la varianza del estimador. Esta es la razón técnica por la que una encuesta con miles de personas es más «eficiente» y nos acerca más a la verdad que una consulta informal: al reducir la varianza, estrechamos el margen de error y ganamos precisión.

Conclusión: una mirada al futuro de las decisiones

La inferencia estadística es la ciencia que se ocupa de gestionar la incertidumbre para alcanzar la precisión. Nos enseña que, si bien es imposible tener certeza absoluta sobre una población masiva, el rigor matemático nos permite actuar con una seguridad asombrosa.

Aceptar que nuestras conclusiones conviven con un nivel de confianza y un riesgo de error no debilita el conocimiento, sino que lo fortalece al hacerlo verificable y científico. La próxima vez que lea el titular de una encuesta electoral o el estudio de un nuevo tratamiento, no se quede en la superficie. Pregúntese: ¿cuál es el margen de error?, ¿es el p-valor realmente significativo? Si posee estas cinco claves, pasará de ser un consumidor pasivo de datos a ser un pensador crítico capaz de ver lo invisible.

En esta conversación puedes escuchar las ideas más interesantes sobre inferencia estadística.

El vídeo resume bien los conceptos más importantes de este tema.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Clasificación y principios fundamentales del diseño experimental

Cuando pensamos en un experimento, solemos imaginar una prueba simple para ver qué opción es “mejor”. Sin embargo, esta visión apenas roza la superficie de una disciplina profunda y estratégica. Existen principios sorprendentes que rigen el diseño experimental y son cruciales no solo para la ciencia, sino también para cualquier toma de decisiones informada. A continuación, se describen brevemente los tipos de experimentos que pueden utilizarse en la investigación científica.

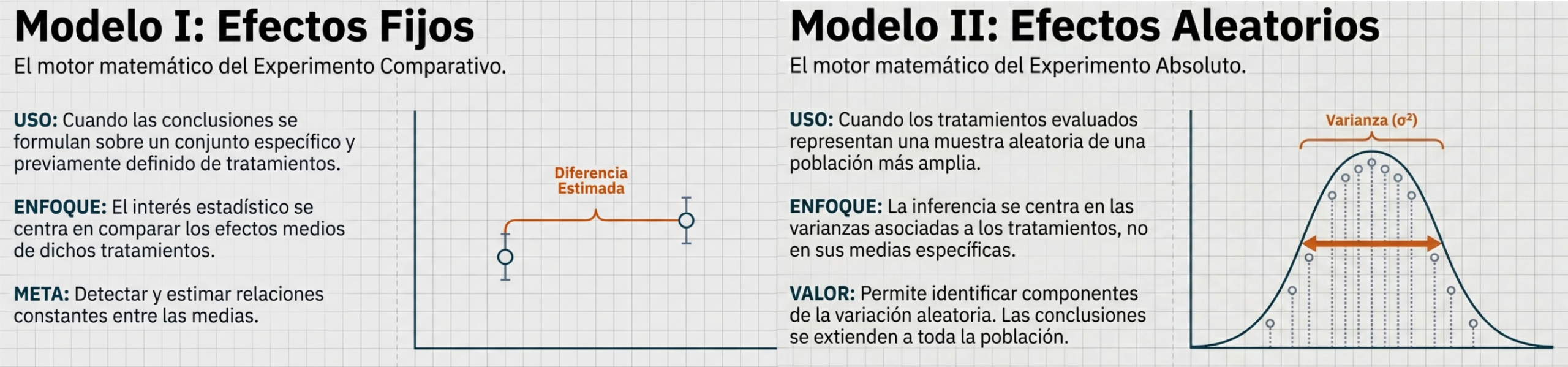
El diseño experimental se clasifica en dos categorías principales, según la propuesta de Anscombe (1947): el experimento absoluto y el experimento comparativo. El experimento absoluto se enfoca en la medición de propiedades físicas constantes para ampliar el conocimiento científico, utilizando un modelo estadístico de efectos aleatorios (Modelo II de Eisenhart), ya que los tratamientos se seleccionan al azar de una población más amplia. Por el contrario, el experimento comparativo está orientado a la toma de decisiones en ciencias aplicadas, con el fin de determinar cuál de varios tratamientos predefinidos es “mejor”. Este enfoque utiliza un modelo de efectos fijos (Modelo I de Eisenhart) y exige una definición precisa del problema para garantizar su validez.

El éxito de un experimento, especialmente el comparativo, depende del cumplimiento de cinco principios fundamentales: simplicidad, nivel de precisión adecuado, ausencia de error sistemático, amplio rango de validez de las conclusiones y una correcta cuantificación de la incertidumbre. La elección del diseño y el modelo estadístico asociado (fijo, aleatorio o mixto) determinan directamente el alcance y la naturaleza de las inferencias que pueden extraerse, vinculando de manera inseparable la planificación experimental con las conclusiones científicas y las decisiones de gestión.

La clasificación propuesta por Anscombe distingue los experimentos en dos grandes tipos según su objetivo fundamental: la adquisición de conocimiento puro o la fundamentación de decisiones prácticas.

Uno de ellos es el llamado experimento absoluto. En este tipo de experimento, el interés principal es medir y conocer las propiedades físicas de una población. Se asume que dichas propiedades permanecen constantes, lo que justifica el uso del término absoluto. El objetivo no es comparar alternativas concretas, sino ampliar el conocimiento científico sobre el fenómeno estudiado.

Los experimentos absolutos suelen centrarse en un solo factor y consideran un número limitado de tratamientos o niveles de ese factor. Estos tratamientos suelen elegirse de forma aleatoria. Por esta razón, si el experimento se repite, no es obligatorio utilizar exactamente los mismos tratamientos en cada ocasión.

Debido a esta forma de selección, los tratamientos se consideran variables aleatorias. En consecuencia, el análisis se basa en un modelo de efectos aleatorios, también conocido como el Modelo II de Eisenhart (1947). Este tipo de modelo permite identificar y estimar los distintos componentes de la variación aleatoria presentes en una población compuesta, lo que constituye un enfoque especialmente útil para muchos problemas de ingeniería.

El experimento comparativo es el segundo tipo de experimento descrito por Anscombe. Este enfoque se utiliza cuando se analizan varios tratamientos y se observa que, aunque los valores absolutos de los resultados pueden fluctuar de forma irregular, las comparaciones relativas entre tratamientos suelen mantenerse estables. En este contexto, es posible concluir que, bajo condiciones similares, algunos tratamientos ofrecen resultados claramente mejores que otros.

Brownlee (1957) sitúa este tipo de experimentos en el ámbito de las ciencias aplicadas, y no es casualidad: la teoría estadística del diseño de experimentos se desarrolló originalmente para responder a las necesidades de este tipo de estudios.

En un experimento comparativo, los tratamientos se evalúan según su efecto promedio sobre una variable de respuesta, con el objetivo principal de determinar cuál es “mejor” según un criterio definido. A diferencia de los experimentos orientados al conocimiento fundamental, aquí el propósito central es apoyar la toma de decisiones prácticas, especialmente las administrativas o de gestión.

Una característica fundamental de los experimentos comparativos es que todos los tratamientos de interés están incluidos explícitamente en el estudio. Por esta razón, el análisis se basa en un modelo de efectos fijos, también conocido como el Modelo I de Eisenhart (1947). Si el experimento se repite, se utilizan exactamente los mismos tratamientos, ya que no se considera una muestra aleatoria. El interés principal radica en detectar y estimar relaciones constantes entre las medias de los tratamientos, lo que conduce naturalmente a la evaluación de hipótesis estadísticas sobre dichas medias.

Para que un experimento comparativo sea válido, debe comenzar con una definición clara y precisa del problema. No basta con plantear de manera general la idea de “comparar tratamientos”. Es imprescindible especificar con detalle los objetivos del estudio y formular con precisión las hipótesis que se probarán. Esta definición inicial determina la población a la que se aplicarán las conclusiones, identifica los factores, los tratamientos y sus niveles, establece las variables de respuesta que se medirán y define qué diferencias entre tratamientos se consideran relevantes. Sin estas especificaciones, no es posible diseñar un experimento adecuado.

Finalmente, una consecuencia natural de los experimentos comparativos es que casi siempre conducen a decisiones concretas. Dado un nivel suficiente de recursos, la hipótesis nula de igualdad entre tratamientos puede rechazarse, lo que obliga a actuar: mantener la situación actual o cambiar a un nuevo tratamiento. Este proceso de decisión consta de dos etapas bien definidas:

Análisis estadístico de los datos, en el que se evalúan las probabilidades asociadas a los resultados y se extraen conclusiones técnicas.
Decisión de gestión en la que, con base en esas conclusiones, se define la acción a realizar.

Esta conexión directa entre el análisis estadístico y la toma de decisiones explica por qué los experimentos comparativos son una herramienta central en la divulgación y la práctica de la ingeniería y de las ciencias aplicadas.

El estadístico cumple un rol clave en el proceso experimental: su responsabilidad es presentar, con la mayor precisión posible, las probabilidades obtenidas en la etapa de análisis, de manera que se reduzca al mínimo la posibilidad de tomar decisiones equivocadas cuando llegue el momento de actuar.

Dado que las decisiones sobre las hipótesis dependen directamente de experimentos cuidadosamente planificados, es esencial que dichos ensayos cumplan con una serie de principios básicos. A continuación se resumen los más importantes, con un enfoque práctico para la ingeniería:

Simplicidad: Tanto la selección de los tratamientos como la organización del experimento deben ser lo más simples posible. Un diseño sencillo facilita el análisis estadístico y la interpretación de los resultados y reduce el riesgo de errores innecesarios.
Nivel de precisión: El experimento debe permitir detectar diferencias entre tratamientos con el grado de precisión que el investigador considere relevante. Para lograrlo, se requiere un diseño experimental adecuado y un número suficiente de repeticiones que garanticen mediciones confiables.
Ausencia de error sistemático: El experimento debe planearse de modo que las unidades experimentales que reciben distintos tratamientos no difieran sistemáticamente entre sí antes de aplicarlos. Este cuidado es fundamental para obtener estimaciones insesgadas del efecto real de cada tratamiento, evitando que factores externos distorsionen los resultados.
Rango de validez de las conclusiones: Las conclusiones del experimento deben ser aplicables a un rango de situaciones lo más amplio posible. Los experimentos replicados y los diseños factoriales ayudan a ampliar este rango de validez, ya que permiten evaluar la consistencia de los resultados bajo diferentes condiciones.
Cuantificación de la incertidumbre: Todo experimento conlleva cierto grado de incertidumbre. Por ello, el diseño debe permitir calcular la probabilidad de que los resultados observados se deban únicamente al azar. Esta cuantificación es esencial para evaluar la solidez de las conclusiones.

Estos principios conducen a una clasificación clásica de los modelos estadísticos, propuesta por Eisenhart (1947), que conecta el diseño del experimento con el tipo de inferencia que se desea realizar:

Modelo de efectos fijos: se utiliza cuando las conclusiones se formulan sobre un conjunto específico y previamente definido de tratamientos. En este caso, el interés estadístico se centra en comparar los efectos medios de dichos tratamientos.
Modelo de efectos aleatorios: se aplica cuando los tratamientos evaluados representan una muestra aleatoria de una población más amplia de tratamientos. Aquí, las conclusiones se extienden más allá de los tratamientos observados y la inferencia se centra en las varianzas asociadas a dichos tratamientos.
Modelo de efectos mixtos: surge cuando el experimento combina tratamientos de efectos fijos y aleatorios en un mismo estudio.

Esta clasificación permite comprender cómo las decisiones sobre el diseño experimental influyen directamente en el tipo de conclusiones que pueden extraerse, un aspecto fundamental tanto en la práctica como en la divulgación de la ingeniería.

En este archivo de audio puedes escuchar una conversación sobre los tipos de experimentos.

En este vídeo se resumen las ideas más importantes sobre este tema.

Referencias:

Anscombe, F. J. (1947). The validity of comparative experiments. Journal of the Royal Statistical Society, 61, 181–211.

Brownlee, K. A. (1957). The principles of experimental design. Industrial Quality Control, 13, 1–9.

Eisenhart, C. (1947). The assumptions underlying the analysis of variance. Biometrics, 3, 1–21.

Melo, O. O., López, L. A., & Melo, S. E. (2007). Diseño de experimentos: métodos y aplicaciones. Universidad Nacional de Colombia. Facultad de Ciencias.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

El impacto del cambio climático en las infraestructuras

DANA OCTUBRE 2024 – Vías del Metro entre Picanya y Paiporta. https://commons.wikimedia.org/

El diseño y la planificación de infraestructuras se han basado históricamente en el análisis de datos climáticos pasados para definir criterios estructurales de seguridad. Sin embargo, la aceleración del cambio climático ha puesto en cuestión la validez de esta metodología y ha obligado a reconsiderar los fundamentos sobre los que se establecen los códigos de construcción y las normativas de diseño. El carácter no estacionario del clima, la creciente magnitud de los eventos meteorológicos extremos y la necesidad de infraestructuras más resilientes han convertido la adaptación al cambio climático en un imperativo técnico y social.

Las estructuras deben garantizar la seguridad de sus ocupantes en condiciones tanto ordinarias como extremas, así como su funcionalidad a lo largo de su ciclo de vida. Es preciso tener en cuenta que la frecuencia y severidad de ciertos fenómenos, como tormentas, inundaciones y variaciones térmicas, ya no pueden preverse con precisión únicamente mediante datos históricos. La integración de modelos de análisis probabilístico y enfoques basados en la fiabilidad estructural representa una vía fundamental para mitigar los riesgos asociados al cambio climático y asegurar la estabilidad y operatividad de infraestructuras críticas en el futuro.

El fin de la estacionariedad climática y sus implicaciones en el diseño estructural

El diseño estructural se ha desarrollado bajo la premisa de que las condiciones climáticas permanecen relativamente estables a lo largo del tiempo, lo que ha permitido definir cargas normativas basadas en registros históricos. No obstante, el cambio climático ha invalidado esta hipótesis al introducir una variabilidad que altera tanto la frecuencia como la intensidad de los fenómenos atmosféricos y compromete la fiabilidad de los métodos de predicción empleados en el ámbito de la ingeniería.

Las estructuras diseñadas bajo códigos convencionales pueden experimentar cargas superiores a las previstas en su diseño original, lo que resulta en un aumento del riesgo estructural y la necesidad de reevaluaciones constantes para garantizar su seguridad. La acumulación de efectos derivados de condiciones climáticas extremas no solo afecta a la estabilidad estructural inmediata, sino que acelera los procesos de deterioro de los materiales y compromete la capacidad de servicio de la infraestructura a largo plazo.

El análisis de la no estacionariedad climática requiere el desarrollo de nuevas herramientas de modelado que permitan proyectar escenarios de carga climática futura con mayor precisión. La variabilidad espacial y temporal de las alteraciones climáticas obliga a establecer criterios de diseño diferenciados según la localización geográfica, la exposición a determinados fenómenos y la importancia funcional de cada infraestructura. En este contexto, la colaboración entre científicos del clima e ingenieros estructurales se erige como un componente esencial para la elaboración de mapas de cargas dinámicos que reflejen las condiciones cambiantes del entorno.

Aumento de cargas climáticas y su impacto en la estabilidad estructural

El cambio climático incide directamente en la magnitud y distribución de las cargas climáticas, lo que supone un desafío significativo para el diseño estructural. El incremento de la temperatura media global y la intensificación de eventos meteorológicos extremos tienen un impacto directo en la resistencia y durabilidad de los materiales de construcción, lo que requiere una revisión exhaustiva de los criterios de diseño para adaptarlos a condiciones más exigentes.

El aumento de la carga de viento, debido a la mayor frecuencia de tormentas severas y huracanes, plantea desafíos particulares para estructuras expuestas a esfuerzos aerodinámicos, tales como rascacielos, puentes y torres de telecomunicaciones. La variabilidad en la dirección y velocidad de los vientos extremos introduce incertidumbre en el diseño convencional, lo que requiere la aplicación de metodologías de análisis probabilístico que permitan anticipar los efectos acumulativos de estas fuerzas sobre los elementos estructurales.

Ciertamente, la carga de nieve y hielo constituye un factor de riesgo cuya evolución en un clima cambiante requiere especial atención. En climas fríos, la combinación de precipitaciones extremas y ciclos de congelación y deshielo genera esfuerzos adicionales sobre cubiertas y soportes, lo que puede ocasionar la fatiga de los materiales y aumentar el riesgo de fallos estructurales. La acumulación de hielo en líneas de transmisión eléctrica y otros elementos de infraestructura crítica puede comprometer su funcionalidad, lo que resalta la necesidad imperante de implementar estrategias de adaptación en el diseño de dichos sistemas.

El aumento del nivel del mar y la intensificación de tormentas costeras representan amenazas crecientes para las infraestructuras situadas en zonas litorales. La erosión del suelo y la intrusión salina pueden afectar la estabilidad de las cimentaciones y las estructuras de contención, mientras que el aumento en la magnitud de las marejadas ciclónicas aumenta el riesgo de colapso en las edificaciones expuestas. Por lo tanto, es esencial adoptar enfoques probabilísticos para estimar las cargas de inundación y considerar criterios de adaptación costera en el diseño estructural, con el fin de mitigar estos efectos y garantizar la seguridad y estabilidad de las infraestructuras en zonas litorales.

Resiliencia estructural y continuidad operativa en escenarios de riesgo creciente

En lo que respecta a la resistencia inmediata de las infraestructuras a eventos climáticos extremos, su capacidad de recuperación y continuidad operativa tras un desastre constituye un aspecto de suma importancia en el contexto del cambio climático. La resiliencia estructural implica no solo garantizar que las edificaciones y redes de transporte soporten cargas excepcionales sin fallar, sino también que puedan volver a estar plenamente operativas en un tiempo razonable tras una interrupción.

La planificación de infraestructuras resilientes requiere un enfoque basado en la funcionalidad tras el desastre, estableciendo criterios de diseño que permitan minimizar los tiempos de inactividad y optimizar los procesos de reparación y reconstrucción. Este enfoque cobra especial relevancia en infraestructuras críticas, tales como hospitales, plantas de tratamiento de agua y redes de energía, cuya operatividad continua resulta esencial para la estabilidad de las comunidades.

El diseño basado en rendimiento (Performance-Based Design, PBD) surge como una herramienta clave para integrar la resiliencia en la ingeniería estructural. A diferencia de los enfoques convencionales basados en requisitos normativos predeterminados, el PBD permite establecer objetivos concretos de rendimiento para cada tipo de estructura, considerando tanto su resistencia ante cargas extremas como su capacidad de recuperación tras eventos disruptivos.

Conclusión: La adaptación de las infraestructuras al cambio climático como una necesidad inaplazable

La evidencia científica sobre el impacto del cambio climático en la infraestructura es concluyente y requiere una revisión exhaustiva de los criterios de diseño estructural. La dependencia exclusiva de datos históricos ya no constituye una estrategia viable en un contexto donde la frecuencia e intensidad de eventos extremos están en constante aumento. Por ello, es necesario implementar análisis probabilísticos, actualizar periódicamente los mapas de cargas climáticas y adoptar estrategias de resiliencia estructural. Estos cambios son fundamentales para garantizar la seguridad y funcionalidad de las infraestructuras en el futuro.

La ingeniería estructural debe evolucionar hacia un enfoque basado en la adaptación y la gestión del riesgo, integrando modelos de predicción climática en el diseño y planificación de nuevas construcciones. La colaboración entre ingenieros, científicos del clima y responsables de políticas públicas será esencial para desarrollar normativas que reflejen la realidad cambiante del entorno y permitan la creación de infraestructuras más seguras y sostenibles.

La adaptación al cambio climático no es únicamente una cuestión técnica, sino una necesidad económica y social que determinará la capacidad de las comunidades para hacer frente a los desafíos del siglo XXI. El diseño estructural del futuro debe asumir este reto con un enfoque proactivo, asegurando que las infraestructuras no solo resistan el clima cambiante, sino que también contribuyan a la estabilidad y el bienestar de la sociedad en su conjunto.

Referencias:

ASCE. (2015). Adapting infrastructure and civil engineering practice to a changing climate. Reston, VA: ASCE.
ASCE. (2018). Climate-resilient infrastructure: Adaptive design and risk management, MOP 140. Reston, VA: ASCE.
ASCE. (2021). Hazard-resilient infrastructures: Analysis and design, MOP 144. Reston, VA: ASCE.
Bruneau, M., Barbato, M., Padgett, J. E., Zaghi, A. E., et al. (2017). State-of-the-art on multihazard design. Journal of Structural Engineering, 143(10), 03117002.
Cooke, R. M. (2015). Messaging climate change uncertainty. Nature Climate Change, 5(1), 8–10.
Ellingwood, B. R., van de Lindt, J. W., & McAllister, T. (2020). Community resilience: A new challenge to the practice of structural engineering. Structural Magazine, 27(11), 28–30.
Ellingwood, B. R., Bocchini, P., Lounis, Z., Ghosn, M., Liu, M., Yang, D., Capacci, L., Diniz, S., Lin, N., Tsiatas, G., Biondini, F., de Lindt, J., Frangopol, D.M., Akiyama, M., Li, Y., Barbato, M., Hong, H., McAllister, T., Tsampras, G. & Vahedifard, F. (2024). Impact of Climate Change on Infrastructure Performance. In Effects of Climate Change on Life-Cycle Performance of Structures and Infrastructure Systems: Safety, Reliability, and Risk (pp. 115-206). Reston, VA: American Society of Civil Engineers.
Eisenhauer, E., Henson, S., Matsler, A., Maxwell, K., Reilly, I., Shacklette, M., Julius, S., Kiessling, B., Fry, M., Nee, R., Bryant, J., Finley, J., & Kieber, B. (2024). Centering equity in community resilience planning: Lessons from case studies. Natural Hazards Forum, Washington, D.C.
IPCC (1997). The regional impacts of climate change: an assessment of vulnerability. IPCC, Geneva.
McAllister, T., Walker, R., & Baker, A. (2022). Assessment of resilience in codes, standards, regulations, and best practices for buildings and infrastructure systems. NIST Technical Note 2209. National Institute of Standards and Technology. https://doi.org/10.6028/NIST.TN.2209
O’Neill, B., van Aalst, M., Zaiton Ibrahim, Z., Berrang Ford, L., Bhadwal, S., Buhaug, H., Diaz, D., Frieler, K., Garschagen, M., Magnan, A., Midgley, G., Mirzabaev, A., Thomas, A., & Warren, R. (2022). Key risks across sectors and regions. In H.-O. Pörtner, D. C. Roberts, M. Tignor, E. S. Poloczanska, K. Mintenbeck, A. Alegría, M. Craig, S. Langsdorf, S. Löschke, V. Möller, A. Okem, & B. Rama (Eds.), Climate change 2022: Impacts, adaptation and vulnerability. Contribution of Working Group II to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change (pp. 2411–2538). Cambridge University Press. https://doi.org/10.1017/9781009325844.025
Poland, C. D. (2009). The resilient city: Defining what San Francisco needs from its seismic mitigation policies. San Francisco Planning and Urban Research Association Report. Earthquake Engineering Research Institute.
Vogel, J., Carney, K. M., Smith, J. B., Herrick, C., et al. (2016). Climate adaptation: The state of practice in US communities. The Kresge Foundation and Abt Associates.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Introducción a los Modelos de Ecuaciones Estructurales (SEM)

Simbología y nomenclatura de los modelos PLS (Aldas, 2018)

Los modelos de ecuaciones estructurales (SEM, por sus siglas en inglés) son una técnica estadística multivariante utilizada para analizar y estimar relaciones causales, combinando datos estadísticos con suposiciones cualitativas sobre la causalidad. Esta metodología es especialmente valiosa en las ciencias sociales, la psicología, el marketing y otras disciplinas en las que las relaciones entre variables no son lineales y pueden involucrar tanto variables observables como latentes. Gracias a los SEM, los investigadores no solo pueden comprobar teorías existentes, sino también desarrollar nuevas hipótesis y modelos que reflejen la realidad de los fenómenos estudiados.

Los modelos de ecuaciones estructurales (MES) combinan el análisis factorial y la regresión lineal para evaluar la correspondencia entre los datos observados y el modelo hipotetizado, que se representa mediante un diagrama de senderos. Los MES proporcionan los valores asociados a cada relación del modelo y un estadístico que mide el ajuste de los datos y valida el modelo.

Una de sus principales fortalezas es la capacidad de construir variables latentes, es decir, variables no observables directamente, sino estimadas a partir de otras que covarían entre sí. Esto permite tener en cuenta explícitamente la fiabilidad del modelo. Además, el análisis factorial, el análisis de caminos y la regresión lineal son casos particulares dentro del enfoque de los MES.

Fundamentos teóricos

Variables latentes y observables:

Variables latentes: son constructos teóricos que no pueden medirse directamente. Por ejemplo, la «satisfacción del cliente» o «lealtad a la marca» son variables latentes que se infieren a partir de las respuestas a encuestas o del comportamiento observable.
Variables observables: son los indicadores que se utilizan para medir las variables latentes. Por ejemplo, en el caso de la satisfacción del cliente, las respuestas a preguntas específicas en una encuesta (como «¿Qué tan satisfecho está con nuestro servicio?»), son variables observables.

Modelo estructural vs. modelo de medida:

Modelo estructural: describe las relaciones causales entre las variables latentes. Este modelo permite a los investigadores establecer hipótesis sobre cómo una variable puede influir en otra.
Modelo de medida: establece cómo se relacionan las variables observables con las variables latentes. Es fundamental validar este modelo para garantizar que los indicadores reflejan realmente el constructo que se pretende medir.

Ejemplo de un modelo de medida y un modelo estructural

Tipos de modelos

Existen dos enfoques principales en SEM:

Análisis de estructuras de covarianza (CB-SEM):

Este enfoque se basa en la matriz de varianza-covarianza y es adecuado para contrastar teorías y probar hipótesis. CB-SEM es una técnica paramétrica que requiere que se cumplan ciertos supuestos estadísticos, como la normalidad multivariada y la independencia de las observaciones.
Aplicaciones: Ideal para estudios confirmatorios donde se busca validar teorías existentes. Se utiliza comúnmente en investigaciones que requieren un alto nivel de rigor estadístico.

Mínimos cuadrados parciales (PLS-SEM):

Este enfoque es más flexible y no requiere los mismos supuestos rigurosos que CB-SEM. PLS-SEM se centra en maximizar la varianza explicada de las variables latentes dependientes a partir de las variables latentes independientes.
Ventajas: Funciona bien con muestras pequeñas y permite la inclusión de constructos formativos, lo que amplía su aplicabilidad en contextos donde los constructos son complejos y multidimensionales.
Aplicaciones: Es especialmente útil en estudios exploratorios y en situaciones donde se busca hacer predicciones, como en el análisis de comportamiento del consumidor.

Metodología de PLS-SEM

La metodología de PLS-SEM se puede resumir en varias etapas clave:

Inicialización: Se obtiene una primera aproximación a los valores de las variables latentes a partir de sus indicadores. Este paso es crucial para establecer un punto de partida en el proceso de estimación.
Estimación de coeficientes de regresión: Se estiman los pesos o coeficientes de regresión de las variables latentes. Este proceso implica calcular las relaciones entre las variables latentes y sus indicadores, así como entre las variables latentes mismas.
Optimización: Se busca maximizar el coeficiente de determinación (R²) de los factores latentes mediante un proceso iterativo. Este proceso de optimización es fundamental para mejorar la precisión de las estimaciones y asegurar que el modelo se ajuste adecuadamente a los datos.
Evaluación de la validez y fiabilidad: Se analizan los constructos para asegurar que miden correctamente lo que se pretende medir. Esto incluye:
—Fiabilidad individual: Evaluación de la consistencia interna de cada indicador utilizando el alfa de Cronbach.
—Validez convergente: Medida a través de la varianza extraída (AVE), que debe ser superior a 0,5 para indicar que los indicadores reflejan el mismo constructo.
—Validez discriminante: Comparación de las correlaciones entre constructos para asegurar que cada constructo es significativamente diferente de los demás. Esto se puede evaluar utilizando el criterio de Fornell-Larcker, que establece que la raíz cuadrada del AVE de cada constructo debe ser mayor que las correlaciones entre constructos.

Ventajas y desventajas de PLS-SEM

Ventajas:

Flexibilidad: PLS-SEM no requiere normalidad multivariada, lo que lo hace más accesible para investigadores en ciencias sociales que trabajan con datos no normales.
Muestras pequeñas: Funciona bien con muestras pequeñas, lo que es ventajoso en estudios exploratorios donde la recolección de datos puede ser limitada.
Constructos formativos: Permite la inclusión de constructos formativos, lo que amplía su aplicabilidad en contextos donde los constructos son complejos y multidimensionales.

Desventajas:

Falta de indicadores de ajuste global: PLS-SEM no proporciona indicadores de ajuste global del modelo, lo que puede limitar la comparación entre modelos y la evaluación de su calidad.
Restricciones en la estructura del modelo: Cada variable latente debe estar conectada a otra mediante una relación estructural, lo que puede ser restrictivo en algunos contextos.
Estimaciones no óptimas: La estimación de parámetros no es óptima en términos de sesgo y consistencia a menos que se utilice el algoritmo PLS consistente, lo que puede afectar la validez de los resultados.

Presentación de resultados

Al presentar los resultados de un análisis SEM, se recomienda estructurarlos en tablas que resuman la fiabilidad y validez del instrumento de medida, así como los análisis de validez discriminante y las hipótesis contrastadas. Así se facilita la comprensión y la interpretación de los resultados por parte de otros investigadores y lectores. La presentación clara y concisa de los resultados es esencial para garantizar la reproducibilidad y la transparencia de la investigación.

Tablas recomendadas:

Tabla de fiabilidad y validez: Resumen de los índices de fiabilidad (alfa de Cronbach, fiabilidad compuesta) y validez (AVE).
Tabla de validez discriminante: Comparación de las correlaciones entre constructos y sus AVE.
Tabla de resultados estructurales: Coeficientes de regresión, R² y significancia de las relaciones estructurales.

Conclusión

Los modelos de ecuaciones estructurales son una herramienta muy valiosa en la investigación social y del comportamiento, ya que permiten a los investigadores modelar y analizar relaciones complejas entre variables. La elección entre CB-SEM y PLS-SEM dependerá de los objetivos de la investigación, la naturaleza de los datos y las hipótesis planteadas. Con una correcta aplicación y validación, SEM puede proporcionar información significativa y fiable en diversas áreas de estudio, contribuyendo al avance del conocimiento en múltiples disciplinas. Para cualquier investigador que busque explorar las complejidades de las relaciones entre variables en su campo de estudio, es esencial comprender profundamente esta metodología y aplicarla correctamente.

Referencias:

Aldás, J. (2018). Modelización estructural mediante Partial Least Squares-PLSPM. Apuntes del seminario de modelización estructural.

Bagozzi, R. P., & Yi, Y. (1988). On the evaluation of structural equation models. Journal of the Academy of Marketing Science, 16(1), 74–94.

Fornell, C., & Bookstein, F. L. (1982). Two structural equation models: LISREL and PLS applied to consumer exit-voice theory. Journal of Marketing Research, 19(4), 440–452.

Hair, J. F., Hult, G. T. M., Ringle, C. M., & Sarstedt, M. (2014). A primer on partial least square structural equation modeling (PLS-SEM). California, United States: Sage.

López, S., & Yepes, V. (2024). Visualizing the future of knowledge sharing in SMEs in the construction industry: A VOS-viewer analysis of emerging trends and best practices. Advances in Civil Engineering, 2024, 6657677.

Yepes, V., & López, S. (2023). The knowledge sharing capability in innovative behavior: A SEM approach from graduate students’ insights. International Journal of Environmental Research and Public Health, 20(2), 1284.

Os dejo a continuación un artículo explicativo al respecto. Espero que os sea de interés.
Pincha aquí para descargar

También os pueden ser útiles algunos vídeos al respecto.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Escalas Likert: una herramienta fundamental en la ingeniería de encuestas

https://delighted.com/es/blog/likert-scale

Las escalas Likert son un estándar en la investigación social, educativa y empresarial gracias a su simplicidad y eficacia para medir percepciones y actitudes. En ingeniería, son fundamentales para recopilar datos en estudios de usabilidad, en la gestión de proyectos y en el análisis de riesgos, entre otros.

Este artículo amplía el debate sobre las escalas Likert, abordando su diseño, implementación, análisis y aplicaciones prácticas en diversos campos de la ingeniería.

¿Qué son las escalas Likert?

De University of Michigan. News and Information Services. Photographs – Bentley Historical Library, CC BY 4.0, https://commons.wikimedia.org/w/index.php?curid=76306573

Desarrolladas por Rensis Likert en 1932, estas escalas son un método para medir actitudes mediante una serie de afirmaciones ante las que el encuestado expresa su nivel de acuerdo o desacuerdo. Generalmente, tienen entre 5 y 7 puntos, aunque en ciertas situaciones se utilizan versiones más específicas. Su unidimensionalidad y simplicidad las hacen ideales para capturar datos subjetivos de forma sistemática.

Las principales características son la unidimensionalidad, ya que los ítems deben medir un único constructo (satisfacción, percepción o actitud), la versatilidad, que permite evaluar dimensiones como la frecuencia, la importancia y la probabilidad en diversos contextos, y la comparabilidad, debido a que la estandarización de las respuestas facilita la comparación entre grupos y estudios a lo largo del tiempo.

Los componentes de una escala Likert incluyen afirmaciones o ítems, que son declaraciones sobre las que el encuestado expresa su nivel de acuerdo o desacuerdo; opciones de respuesta, que representan un rango de valores como «Totalmente en desacuerdo», «Neutral» y «Totalmente de acuerdo»; y la puntuación, en la que las respuestas se codifican numéricamente para facilitar el análisis estadístico.

El diseño de un cuestionario con escala Likert

El diseño de un cuestionario bien estructurado es fundamental para garantizar la calidad de los datos recopilados. Esto incluye desde la redacción de las preguntas hasta la elección del tipo de respuesta.

Redacción de ítems: La calidad de un cuestionario depende de la claridad y precisión de sus elementos, por lo que se recomienda evitar ambigüedades, expresar una sola idea por ítem, utilizar afirmaciones neutrales para minimizar sesgos emocionales y adaptar el lenguaje al contexto, teniendo en cuenta el nivel de comprensión del grupo objetivo. Por ejemplo, la pregunta «Estoy satisfecho con la calidad y el precio del servicio» debería descomponerse en dos preguntas distintas. Formulaciones como «¿Está de acuerdo con que los políticos son corruptos?» introducen sesgos emocionales.
Opciones de respuesta: Para diseñar opciones de respuesta efectivas, es relevante que sean claras, equidistantes y exhaustivas. El número de categorías debe tenerse en cuenta; cinco es el estándar, mientras que escalas de siete puntos ofrecen mayor precisión y escalas con menos de tres puntos limitan la variabilidad. Además, elegir entre escalas pares o impares influye en los resultados: las pares eliminan el punto medio neutro, lo que obliga a los encuestados a posicionarse en uno de los dos extremos.
Organización y estructura: La organización y estructura de un cuestionario deben seguir un flujo lógico, aplicando la técnica del embudo, que consiste en comenzar con preguntas generales y poco sensibles, avanzar hacia ítems más específicos y personales y agrupar por temas para mantener la coherencia y reducir la fatiga cognitiva.
Realización de pretests: Es esencial para evaluar la comprensión, la fluidez y la relevancia del cuestionario, lo que permite identificar y corregir errores antes de su implementación final.

De Nicholas Smithvectorization: Trabajo propio – Trabajo propio, based on File:Example Likert Scale.jpg, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=18615046

Análisis de datos obtenidos con escalas Likert

La fortaleza de las escalas Likert radica en su capacidad para adaptarse a diversos métodos analíticos. Los datos obtenidos pueden proporcionar información valiosa, ya sea en análisis descriptivos o en modelos avanzados.

1. Análisis descriptivo

Tendencia central: La media y la mediana resumen la tendencia general de las respuestas.
Dispersión: Indicadores como el rango o la desviación estándar ayudan a comprender la variabilidad de las respuestas.
Visualización: Gráficos de barras, histogramas y diagramas de cajas facilitan la interpretación rápida.

2. Relación entre variables

El análisis bivariado permite explorar cómo se relacionan diferentes variables dentro de la escala Likert:

Correlación de Pearson: evalúa la relación lineal entre dos variables continuas.
Tablas de contingencia: adecuadas para analizar categorías derivadas de respuestas de Likert.

3. Análisis factorial exploratorio (AFE)

Este enfoque permite identificar dimensiones latentes que subyacen en los ítems:

Validación estructural: Determina si los ítems agrupan un único constructo o múltiples dimensiones.
Técnicas de reducción: PCA (Análisis de Componentes Principales) y AFE ayudan a simplificar la interpretación.

4. Evaluación de la fiabilidad

La consistencia interna de una escala se mide comúnmente mediante el alfa de Cronbach. Valores superiores a 0,7 suelen considerarse aceptables.

Ventajas y limitaciones

Entre sus ventajas destacan su accesibilidad, ya que son fáciles de implementar y de entender, su flexibilidad, al adaptarse a diversas áreas de investigación, y su simplicidad analítica, que permite análisis tanto básicos como avanzados. Sin embargo, presentan limitaciones: la deseabilidad social, donde las respuestas pueden estar influenciadas por lo que es socialmente aceptable; la ambigüedad en las opciones medias, ya que categorías como «Neutral» pueden interpretarse de manera diferente; y la unidimensionalidad no garantizada, por lo que es necesario validar su estructura interna mediante análisis factorial.

Aplicaciones en ingeniería

Las escalas Likert tienen amplias aplicaciones en ingeniería, por ejemplo, en estudios de satisfacción para evaluar la percepción de los usuarios sobre productos o servicios, en gestión de riesgos para analizar actitudes hacia posibles escenarios de riesgo en proyectos y en usabilidad de software para medir la experiencia del usuario en el diseño y la funcionalidad de las interfaces. En la evaluación de proyectos, sirven para recopilar información sobre aspectos como el cumplimiento de plazos, la calidad del producto y la eficiencia del equipo.

Conclusión

Las escalas de Likert son una herramienta esencial para medir percepciones, actitudes y comportamientos. Su versatilidad y facilidad de implementación las convierten en una opción popular en investigaciones de ingeniería y de ciencias sociales. El diseño riguroso del cuestionario y el análisis adecuado de los datos garantizan resultados fiables que pueden orientar la toma de decisiones, mejorando procesos y productos en diversos ámbitos de la ingeniería.

A continuación, os dejo una presentación que hice en Santiago de Chile sobre el análisis de cuestionarios basados en escalas de Likert. Espero que sea de vuestro interés.

Pincha aquí para descargar

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Población y muestra, parámetros y estadísticos

Figura 1. Población y muestra. https://proyectodescartes.org/iCartesiLibri/

En cualquier investigación estadística, se recopila información de un conjunto de elementos específicos. Una población se define como un conjunto completo de posibles individuos, especímenes, objetos o medidas de interés que se someten a un estudio para ampliar nuestro conocimiento sobre ellos. En el caso de poblaciones finitas y de tamaño reducido, es factible medir a todos los individuos para obtener un conocimiento preciso de sus características, también conocidas como parámetros. Por ejemplo, se podría analizar la proporción de productos defectuosos o calcular la media de alguna variable relacionada con los productos.

Por otro lado, cuando la población es infinita o muy numerosa, resulta impracticable o costoso medir a todos los individuos. En tales circunstancias, es necesario extraer una muestra representativa de la población y, basándonos en las características observadas en dicha muestra (conocidas como estadísticos), podemos realizar inferencias sobre los parámetros que describen a la población en su totalidad. De manera figurativa, podríamos comparar una muestra, que se supone representativa de una población, con lo que una maqueta representa respecto al edificio que retrata. La calidad de la muestra, al igual que la de la maqueta, dependerá del grado de representatividad que pueda ofrecer.

En términos generales, la inferencia estadística es el proceso de utilizar estadísticos de una muestra para hacer deducciones acerca de la distribución de probabilidad de una población. Si estas deducciones se efectúan sobre parámetros poblacionales, este proceso se denomina inferencia estadística paramétrica. Si las deducciones se hacen sobre la distribución de probabilidad completa, sin hacer referencia a parámetros específicos, se le llama inferencia estadística no paramétrica.

Dentro del ámbito industrial, las poblaciones de interés abarcan una amplia gama de elementos, que incluyen materiales, productos terminados, partes o componentes, así como procesos, entre otros. En muchas ocasiones, estas poblaciones se caracterizan por ser infinitas o de gran magnitud. Por ejemplo, en la elaboración del hormigón en una planta, resulta inviable, o al menos poco práctico, medir la resistencia a la compresión simple de cada una de las muestras que podrían obtenerse en una amasada. Incluso en situaciones donde la producción no sea masiva, es recomendable pensar en el proceso como si fuera una población infinita o de gran escala, dado que la producción puede continuar sin interrupciones, es decir, no existe un último artículo mientras la empresa siga en funcionamiento. Un ejemplo sería la fabricación de bloques de hormigón en una empresa de prefabricados. En tales circunstancias, los procesos se evalúan mediante muestras de productos extraídas en algún punto específico del proceso.

Un punto crucial a considerar es la obtención de muestras que sean verdaderamente representativas, es decir, que capturen de manera adecuada los aspectos clave que se desean analizar en la población. Para lograr esta representatividad, resulta esencial diseñar un proceso de muestreo aleatorio de manera apropiada. En este tipo de muestreo, se evita cualquier tipo de sesgo que pudiera favorecer la inclusión de elementos particulares, asegurando que todos los elementos de la población tengan las mismas oportunidades de formar parte de la muestra.

Existen varias técnicas de muestreo aleatorio, como el muestreo simple, el muestreo estratificado, el muestreo sistemático y el muestreo por conglomerados. Cada una de estas metodologías se adapta a los objetivos específicos del estudio, así como a las circunstancias y características particulares de la población, garantizando de esta manera que las muestras obtenidas sean verdaderamente representativas.

No obstante, en la práctica, la hipótesis de un muestreo aleatorio suele quedar lejos de cumplirse al lidiar con datos del mundo real. Un ejemplo ilustrativo son los registros de la temperatura diaria. En estos registros, los días calurosos tienden a agruparse, lo que significa que los valores elevados tienden a seguir a otros valores elevados. A este fenómeno se le denomina autocorrelación, y por ende, estos datos no pueden considerarse como el resultado de extracciones aleatorias. La validez de la hipótesis de muestreo aleatorio desempeña un papel fundamental tanto en el análisis como en el diseño de experimentos científicos o en el ámbito del control de la calidad.

La importancia de la aleatoriedad se destaca de manera clara en situaciones cotidianas. Por ejemplo, al seleccionar una muestra de ladrillos de un palet, si optamos por los que se encuentran en la parte superior, podríamos introducir un sesgo en nuestros resultados. Es lamentable que en muchos trabajos estadísticos, la hipótesis de muestreo aleatorio se trate como si fuera una característica inherente de los datos naturales. En realidad, cuando trabajamos con datos reales, la aleatoriedad no es una propiedad en la que podamos confiar de manera absoluta. Sin embargo, con las precauciones adecuadas en el diseño experimental o en la toma de muestras de un control estadístico de la calidad, esta suposición puede seguir siendo relevante y útil.

Os dejo a continuación un vídeo explicativo, que espero os sea de interés.

[media]dff702a0-f6a7-11ea-9fbd-f90680954ff3:640:360[/media]

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

¿Qué hacemos con los valores atípicos (outliers)?

Figura 1. Valor atípico en el diagrama de caja y bigotes

Un valor atípico (outlier, en inglés) es una observación que numéricamente es muy distinta al resto de elementos de una muestra. Estos datos nos pueden causar problemas en la interpretación de lo que ocurre en un proceso o en una población. Por ejemplo, en el cálculo de la resistencia media a compresión simple de unas probetas de hormigón, la mayoría se encuentran entre 25 y 30 MPa. ¿Qué ocurriría si, de repente, medimos una probeta con una resistencia de 60 MPa? La mediana de los datos puede ser 27 MPa, pero la resistencia media podría llegar a 45 MPa. En este caso, la mediana refleja mejor el valor central de la muestra que la media.

La pregunta que nos podemos plantear es inmediata. ¿Qué hacemos con esos valores atípicos? La opción de ignorarlos a veces no es la mejor de las soluciones posibles si pretendemos conocer qué ha pasado con estos valores. Lo bien cierto es que distorsionan los resultados del análisis, por lo que hay que identificarlos y tratarlos de forma adecuada. A veces se excluyen si son resultado de un error, pero otras veces son datos potencialmente interesantes en la detección de anomalías.

Los valores atípicos pueden deberse a errores en la recolección de datos válidos que muestran un comportamiento diferente, pero reflejan la aleatoriedad de la variable en estudio. Es decir, valores que pueden haber aparecido como parte del proceso, aunque parezcan extraños. Si los valores atípicos son parte del proceso, deben conservarse. En cambio, si ocurren por algún tipo de error (medida, codificación…), lo adecuado es su eliminación. En la Tabla 1 se recogen algunas de las causas comunes de los valores atípicos y sus acciones posibles.

Tabla 1. Causas comunes de los valores atípicos. Fuente: Soporte de Minitab(R) 18.

Causa	Acciones posibles
Error de entrada de datos	Corregir el error y volver a analizar los datos.
Problema del proceso	Investigar el proceso para determinar la causa del valor atípico.
Factor faltante	Determinar si no se consideró un factor que afecta el proceso.
Probabilidad aleatoria	Investigar el proceso y el valor atípico para determinar si este se produjo en virtud de las probabilidades; realice el análisis con y sin el valor atípico para ver su impacto en los resultados.

Los valores atípicos a veces son subjetivos y existen numerosos métodos para clasificarlos. La detección de valores atípicos se puede realizar a nivel univariante usando gráficos sencillos como histogramas o diagramas de caja y bigotes. A nivel bivariante se pueden localizar mediante análisis de diagrama de dispersión o análisis de los residuos. En el ámbito multivariante se pueden descubrir los valores atípicos mediante un análisis de la matriz de residuos.

El método más habitual por su sencillez y resultados es el test de Tukey, que toma como referencia la diferencia entre el primer cuartil (Q1) y el tercer cuartil (Q3), o rango intercuartílico. En un diagrama de caja se considera un valor atípico el que se encuentra 1,5 veces esa distancia de uno de esos cuartiles (atípico leve) o a 3 veces esa distancia (atípico extremo). Se trata de un método paramétrico que supone que la población es normal (Figura 2). No obstante, también existen métodos no paramétricos cuando la muestra no supere la prueba de normalidad correspondiente.

Figura 2. Detección paramétrica de valores atípicos, basado en la curva de distribución normal. Wikipedia

Os dejo algún vídeo donde se explica cómo detectar los valores atípicos.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

¿Cuántas respuestas son necesarias en una encuesta? Pues depende.

A veces me toca dirigir algún trabajo de investigación de mis estudiantes que trata de conocer la opinión sobre algún aspecto concreto. Normalmente se trata de temas relacionados con el sector de la construcción, aunque también suelo investigar si ha tenido éxito algún tipo de innovación educativa en mis clases. Para ello suelo aconsejar el uso de cuestionarios basados en escalas Likert, pues de esta forma facilito el análisis estadístico multivariante de los resultados.

El problema siempre es el mismo: ¿Profesor, tengo suficientes encuestas o tengo que enviar más encuestas? Y la respuesta siempre es la misma: depende del objeto de la encuesta. Vamos a analizar esto por partes.

Si se trata de describir los resultados obtenidos de un grupo de estudio, la muestra representa a la totalidad de la población, y por tanto no es necesario alcanzar un número de respuestas mínimo. Por ejemplo, si en una asociación de empresarios de la construcción el número de socios es de 30 y todos responden el cuestionario, es evidente que los resultados del estudio representan de forma exacta lo que opinan los 30 socios.

Sin embargo, lo habitual es encontrarse con un número de respuestas que forman una muestra de una población. Aquí se trata de saber si podemos extrapolar los resultados a la población que representa la muestra. Para ello nos debemos hacer dos preguntas: ¿Es la muestra representativa? ¿Cuál es el margen de error que cometemos?

Las técnicas de muestreo permiten extraer muestras representativas. Estos muestreos pueden ser probabilísticos o no probabilísticos. Entre los primeros podemos resaltar el muestreo aleatorio sistemático, el estratificado o el muestreo por conglomerados. Entre los no probabilísticos, el muestreo por cuotas, por bola de nieve o el muestreo subjetivo por decisión razonada. Remito a los interesados a bibliografía específica, pues se escapa al objetivo de este artículo.

Aquí vamos a comentar brevemente lo relativo al error muestral. El error muestral se corresponde con el margen de error que estamos dispuestos a aceptar. Por ejemplo, si decimos que el 15% de la población está de acuerdo con algo y el error muestral es del 4%, realmente dicha opinión se encuentra entre el 11% y el 19% para un nivel de confianza determinado. Por eso, lo primero, será definir el nivel de confianza o riesgo de primera especie «z», que sería el riesgo que aceptamos de equivocarnos al presentar nuestros resultados. El nivel de confianza habitual es 1 – α = 95% o α = 5%. Se utiliza como «z», que es un valor de la distribución normal asociado a una determinada probabilidad de ocurrencia. Así, z=1,96 si 1 – α = 95%, z=2,00 si 1 – α = 95,5% y z=2,57 si 1 – α = 99%.

Otro factor a tener en cuenta es la variabilidad de las respuestas estimada en la población. Si sabemos que todos los sujetos piensan lo mismo, nos bastará preguntar a uno solo o a muy pocos. Pero si sabemos que habrá una gran diversidad de respuestas, hará falta una mayor número de sujetos en la muestra. Como lo normal es desconocer la variabilidad de las respuestas en la población, elegimos la mayor varianza posible p=q=50% (sería que el 50% respondiera que «sí» y el otro 50% lo contrario).

Las fórmulas que nos dan el error muestral, por tanto, dependen de los factores anteriores y también de conocer si la población es finita o infinita (más de 30.000 individuos ya se considera como infinita). En la figura se indican ambas fórmulas.

Fórmulas del error muestral, en función de si la población es finita o infinita

Si jugamos un poco con estas fórmulas, veremos que para un nivel de confianza del 95%, serían necesarias 96 respuestas en una población infinita y 95 respuestas en una población de un tamaño de 10.000 (casi coinciden) para un error muestral del 10%. Pero si queremos bajar el error al 5%, se eleva el número de respuestas a 384 en el caso de la población infinita y a 370 en el caso de una población finita de 10.000. Como vemos, se dispara el número de respuestas necesarias para reducir el error.

Por tanto, mi respuesta a mis estudiantes suele ser siempre la misma: vamos a intentar llegar a 100 respuestas para empezar a tener un error razonable.

En apretada síntesis, os quiero dar las siguientes consideraciones sobre el muestreo:

No solo es necesario que el tamaño de la muestra sea suficiente, sino también que la muestra sea representativa de la población que tratamos de describir
Una muestra de gran tamaño no garantiza que el margen de error sea pequeño, pues puede estar sesgada hacia segmentos de la población representados en exceso o poco representados
Si la población a estudiar es demasiado grande es recomendable segmentarla en estratos y valorar en cuáles de ellos pueden obtenerse muestras representativas, facilitando así una interpretación de los resultados más precisa
En general, el margen de error en cada estrato suele ser superior al margen de error de toda la muestra en conjunto. Es recomendable ser consciente de esta diferencia de precisión en la interpretación de resultados

Pues ahora una reflexión final: ¿Qué error tienen las encuestas que contestan los alumnos en relación con la calidad del profesor? ¿Es razonable tomar decisiones respecto a la continuidad o no de un profesor teniendo en cuenta estas encuestas? Tenéis las claves releyendo el artículo.

Aquí tenéis un vídeo sobre las técnicas de muestreo.

Os dejo a continuación un pequeño vídeo sobre el error de muestreo.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.