diseño de experimentos archivos - El blog de Víctor Yepes

Unidades experimentales y muestrales en el diseño de experimentos

La unidad experimental (UE) es el elemento central en el diseño y el análisis de experimentos comparativos. Se define como la entidad a la que se le puede asignar un tratamiento de forma independiente y sobre la cual se realizan las mediciones. La identificación correcta de la UE es fundamental, ya que la estimación de la variabilidad natural, conocida como error experimental, depende exclusivamente de la comparación entre unidades experimentales idénticas que reciben el mismo tratamiento.

Una unidad experimental puede contener múltiples unidades muestrales, subelementos que reciben obligatoriamente el mismo tratamiento que la UE a la que pertenecen. Por esta razón, la variabilidad entre estas unidades muestrales internas no resulta útil para estimar el efecto del tratamiento. Un diseño experimental sólido se basa en la capacidad de distinguir los efectos reales de los tratamientos del «ruido» natural del sistema, una distinción que solo es posible mediante la correcta cuantificación de la variabilidad entre las unidades experimentales completas.

Definiciones fundamentales

El marco de un experimento se define a través de sus componentes básicos, en los que la unidad experimental y la unidad muestral desempeñan funciones distintas, aunque interconectadas.

1. La unidad experimental (UE)

La unidad experimental es el pilar de cualquier ensayo comparativo. Su definición formal es la siguiente:

«El elemento sobre el que se realizan las mediciones y al que se puede asignar un tratamiento de forma independiente».

El conjunto de todas las unidades experimentales disponibles para un estudio se denomina material experimental. La definición de una UE es flexible y se adapta a los objetivos de la investigación.

Ejemplos prácticos:

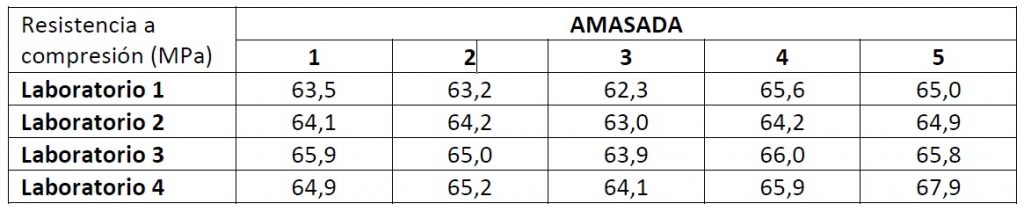
Ensayo de resistencia del hormigón: la unidad experimental puede ser un bloque o un cilindro de hormigón elaborado con una mezcla específica. Las unidades muestrales serían las probetas o las muestras extraídas del mismo bloque para realizar ensayos de compresión o de flexión.
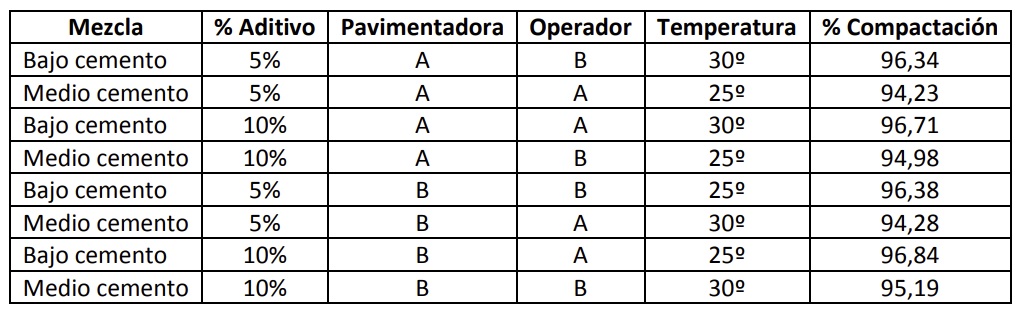
Prueba de rendimiento de pavimentos: la unidad experimental puede ser un tramo de vía construido con un diseño o material específico (por ejemplo, un segmento de 50 metros). Las unidades muestrales serían los puntos de medición dentro del tramo, por ejemplo, las deflexiones o la rugosidad.
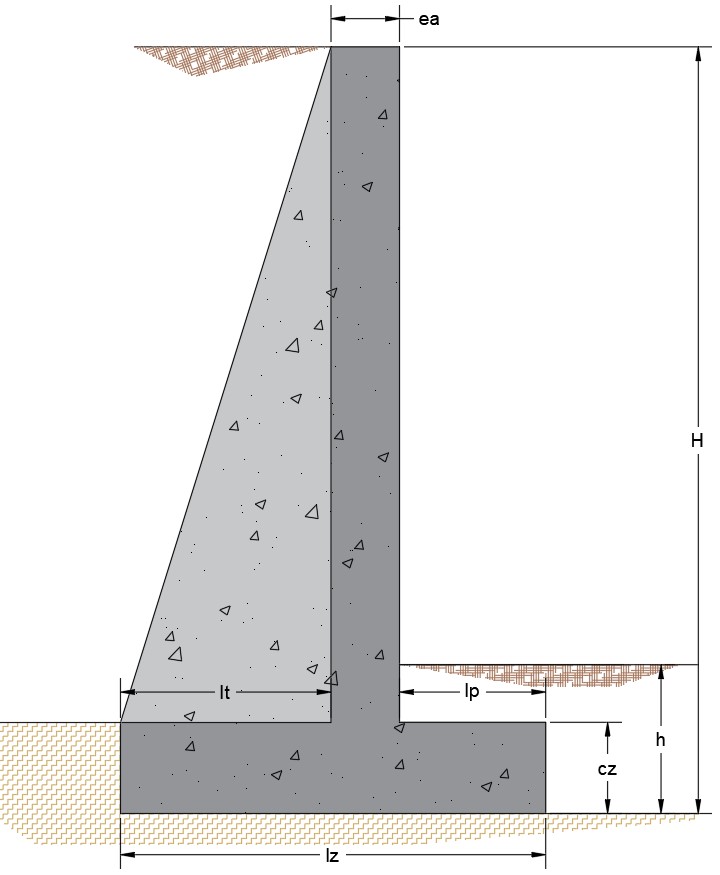
Ensayo de estructuras a escala en laboratorio: la unidad experimental puede ser una viga o una columna, construida según un diseño específico. Las unidades muestrales serían los puntos de medición (deformaciones, desplazamientos o tensiones) registrados por sensores a lo largo de la estructura.

El criterio esencial para definir una UE es que sea capaz de recibir diferentes tratamientos de manera independiente de las demás unidades.

2. La unidad muestral.

Dentro de una unidad experimental pueden existir subelementos en los que se aplican las condiciones experimentales. A estos se les conoce como unidades muestrales.

La regla fundamental que las rige es que todas las unidades muestrales de una misma unidad experimental deben recibir el mismo tratamiento. Como consecuencia directa, la asignación del tratamiento a estas subunidades no es independiente entre sí, lo que tiene implicaciones críticas para el análisis estadístico.

El papel de la estimación en la variabilidad.

La distinción entre unidades experimentales y muestrales es crucial para inferir correctamente los efectos de un tratamiento, ya que incide directamente en la medición de la variabilidad del sistema.

a. El error experimental

Para evaluar si un tratamiento tiene un efecto real, es necesario conocer la variabilidad natural del material experimental. Esta variabilidad inherente se conoce como error experimental. Es la base contra la que se comparan las diferencias observadas entre los tratamientos.

b. Metodología de estimación

La estimación correcta del error experimental solo se logra a partir de las diferencias observadas entre unidades experimentales que, en principio, son idénticas y han recibido el mismo tratamiento.

Fuente de estimación válida: la variación entre unidades experimentales es la única que permite estimar correctamente el error experimental.
Fuente de estimación no válida: la variación entre las unidades muestrales dentro de una misma unidad experimental es, por lo general, muy pequeña y no proporciona información útil para estimar el efecto del tratamiento ni el error experimental.

La observación clave es que «solo la unidad experimental completa permite estimar correctamente el error experimental».

Tipología de variables en un experimento.

Los datos recopilados en un experimento se organizan en dos categorías principales de variables:

Tipo de variable	Descripción
Variables de respuesta	Son las mediciones obtenidas de las unidades experimentales. Sus valores reflejan tanto los efectos de los tratamientos como la variabilidad natural del sistema.
Variables explicativas (factores)	Son las variables que se manipulan o controlan porque se cree que influyen en las variables de respuesta. Incluyen los factores de clasificación, que definen los niveles o categorías sobre los cuales se realizan las inferencias estadísticas.

Conclusión: el fundamento de un diseño sólido.

La estructura de un diseño experimental robusto se basa en comparar unidades experimentales similares. Este enfoque permite a los investigadores distinguir de manera fiable el efecto real de los tratamientos aplicados del «ruido» o de la variabilidad natural inherente al sistema experimental. Por tanto, la identificación precisa y la gestión adecuada de la unidad experimental no son meros detalles técnicos, sino requisitos indispensables para que las conclusiones científicas derivadas del experimento sean válidas y fiables.

En este documento tenéis un resumen de las ideas más importantes.

Pincha aquí para descargar

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Clasificación y principios fundamentales del diseño experimental

Cuando pensamos en un experimento, solemos imaginar una prueba simple para ver qué opción es “mejor”. Sin embargo, esta visión apenas roza la superficie de una disciplina profunda y estratégica. Existen principios sorprendentes que rigen el diseño experimental y son cruciales no solo para la ciencia, sino también para cualquier toma de decisiones informada. A continuación, se describen brevemente los tipos de experimentos que pueden utilizarse en la investigación científica.

El diseño experimental se clasifica en dos categorías principales, según la propuesta de Anscombe (1947): el experimento absoluto y el experimento comparativo. El experimento absoluto se enfoca en la medición de propiedades físicas constantes para ampliar el conocimiento científico, utilizando un modelo estadístico de efectos aleatorios (Modelo II de Eisenhart), ya que los tratamientos se seleccionan al azar de una población más amplia. Por el contrario, el experimento comparativo está orientado a la toma de decisiones en ciencias aplicadas, con el fin de determinar cuál de varios tratamientos predefinidos es “mejor”. Este enfoque utiliza un modelo de efectos fijos (Modelo I de Eisenhart) y exige una definición precisa del problema para garantizar su validez.

El éxito de un experimento, especialmente el comparativo, depende del cumplimiento de cinco principios fundamentales: simplicidad, nivel de precisión adecuado, ausencia de error sistemático, amplio rango de validez de las conclusiones y una correcta cuantificación de la incertidumbre. La elección del diseño y el modelo estadístico asociado (fijo, aleatorio o mixto) determinan directamente el alcance y la naturaleza de las inferencias que pueden extraerse, vinculando de manera inseparable la planificación experimental con las conclusiones científicas y las decisiones de gestión.

La clasificación propuesta por Anscombe distingue los experimentos en dos grandes tipos según su objetivo fundamental: la adquisición de conocimiento puro o la fundamentación de decisiones prácticas.

Uno de ellos es el llamado experimento absoluto. En este tipo de experimento, el interés principal es medir y conocer las propiedades físicas de una población. Se asume que dichas propiedades permanecen constantes, lo que justifica el uso del término absoluto. El objetivo no es comparar alternativas concretas, sino ampliar el conocimiento científico sobre el fenómeno estudiado.

Los experimentos absolutos suelen centrarse en un solo factor y consideran un número limitado de tratamientos o niveles de ese factor. Estos tratamientos suelen elegirse de forma aleatoria. Por esta razón, si el experimento se repite, no es obligatorio utilizar exactamente los mismos tratamientos en cada ocasión.

Debido a esta forma de selección, los tratamientos se consideran variables aleatorias. En consecuencia, el análisis se basa en un modelo de efectos aleatorios, también conocido como el Modelo II de Eisenhart (1947). Este tipo de modelo permite identificar y estimar los distintos componentes de la variación aleatoria presentes en una población compuesta, lo que constituye un enfoque especialmente útil para muchos problemas de ingeniería.

El experimento comparativo es el segundo tipo de experimento descrito por Anscombe. Este enfoque se utiliza cuando se analizan varios tratamientos y se observa que, aunque los valores absolutos de los resultados pueden fluctuar de forma irregular, las comparaciones relativas entre tratamientos suelen mantenerse estables. En este contexto, es posible concluir que, bajo condiciones similares, algunos tratamientos ofrecen resultados claramente mejores que otros.

Brownlee (1957) sitúa este tipo de experimentos en el ámbito de las ciencias aplicadas, y no es casualidad: la teoría estadística del diseño de experimentos se desarrolló originalmente para responder a las necesidades de este tipo de estudios.

En un experimento comparativo, los tratamientos se evalúan según su efecto promedio sobre una variable de respuesta, con el objetivo principal de determinar cuál es “mejor” según un criterio definido. A diferencia de los experimentos orientados al conocimiento fundamental, aquí el propósito central es apoyar la toma de decisiones prácticas, especialmente las administrativas o de gestión.

Una característica fundamental de los experimentos comparativos es que todos los tratamientos de interés están incluidos explícitamente en el estudio. Por esta razón, el análisis se basa en un modelo de efectos fijos, también conocido como el Modelo I de Eisenhart (1947). Si el experimento se repite, se utilizan exactamente los mismos tratamientos, ya que no se considera una muestra aleatoria. El interés principal radica en detectar y estimar relaciones constantes entre las medias de los tratamientos, lo que conduce naturalmente a la evaluación de hipótesis estadísticas sobre dichas medias.

Para que un experimento comparativo sea válido, debe comenzar con una definición clara y precisa del problema. No basta con plantear de manera general la idea de “comparar tratamientos”. Es imprescindible especificar con detalle los objetivos del estudio y formular con precisión las hipótesis que se probarán. Esta definición inicial determina la población a la que se aplicarán las conclusiones, identifica los factores, los tratamientos y sus niveles, establece las variables de respuesta que se medirán y define qué diferencias entre tratamientos se consideran relevantes. Sin estas especificaciones, no es posible diseñar un experimento adecuado.

Finalmente, una consecuencia natural de los experimentos comparativos es que casi siempre conducen a decisiones concretas. Dado un nivel suficiente de recursos, la hipótesis nula de igualdad entre tratamientos puede rechazarse, lo que obliga a actuar: mantener la situación actual o cambiar a un nuevo tratamiento. Este proceso de decisión consta de dos etapas bien definidas:

Análisis estadístico de los datos, en el que se evalúan las probabilidades asociadas a los resultados y se extraen conclusiones técnicas.
Decisión de gestión en la que, con base en esas conclusiones, se define la acción a realizar.

Esta conexión directa entre el análisis estadístico y la toma de decisiones explica por qué los experimentos comparativos son una herramienta central en la divulgación y la práctica de la ingeniería y de las ciencias aplicadas.

El estadístico cumple un rol clave en el proceso experimental: su responsabilidad es presentar, con la mayor precisión posible, las probabilidades obtenidas en la etapa de análisis, de manera que se reduzca al mínimo la posibilidad de tomar decisiones equivocadas cuando llegue el momento de actuar.

Dado que las decisiones sobre las hipótesis dependen directamente de experimentos cuidadosamente planificados, es esencial que dichos ensayos cumplan con una serie de principios básicos. A continuación se resumen los más importantes, con un enfoque práctico para la ingeniería:

Simplicidad: Tanto la selección de los tratamientos como la organización del experimento deben ser lo más simples posible. Un diseño sencillo facilita el análisis estadístico y la interpretación de los resultados y reduce el riesgo de errores innecesarios.
Nivel de precisión: El experimento debe permitir detectar diferencias entre tratamientos con el grado de precisión que el investigador considere relevante. Para lograrlo, se requiere un diseño experimental adecuado y un número suficiente de repeticiones que garanticen mediciones confiables.
Ausencia de error sistemático: El experimento debe planearse de modo que las unidades experimentales que reciben distintos tratamientos no difieran sistemáticamente entre sí antes de aplicarlos. Este cuidado es fundamental para obtener estimaciones insesgadas del efecto real de cada tratamiento, evitando que factores externos distorsionen los resultados.
Rango de validez de las conclusiones: Las conclusiones del experimento deben ser aplicables a un rango de situaciones lo más amplio posible. Los experimentos replicados y los diseños factoriales ayudan a ampliar este rango de validez, ya que permiten evaluar la consistencia de los resultados bajo diferentes condiciones.
Cuantificación de la incertidumbre: Todo experimento conlleva cierto grado de incertidumbre. Por ello, el diseño debe permitir calcular la probabilidad de que los resultados observados se deban únicamente al azar. Esta cuantificación es esencial para evaluar la solidez de las conclusiones.

Estos principios conducen a una clasificación clásica de los modelos estadísticos, propuesta por Eisenhart (1947), que conecta el diseño del experimento con el tipo de inferencia que se desea realizar:

Modelo de efectos fijos: se utiliza cuando las conclusiones se formulan sobre un conjunto específico y previamente definido de tratamientos. En este caso, el interés estadístico se centra en comparar los efectos medios de dichos tratamientos.
Modelo de efectos aleatorios: se aplica cuando los tratamientos evaluados representan una muestra aleatoria de una población más amplia de tratamientos. Aquí, las conclusiones se extienden más allá de los tratamientos observados y la inferencia se centra en las varianzas asociadas a dichos tratamientos.
Modelo de efectos mixtos: surge cuando el experimento combina tratamientos de efectos fijos y aleatorios en un mismo estudio.

Esta clasificación permite comprender cómo las decisiones sobre el diseño experimental influyen directamente en el tipo de conclusiones que pueden extraerse, un aspecto fundamental tanto en la práctica como en la divulgación de la ingeniería.

En este archivo de audio puedes escuchar una conversación sobre los tipos de experimentos.

En este vídeo se resumen las ideas más importantes sobre este tema.

Referencias:

Anscombe, F. J. (1947). The validity of comparative experiments. Journal of the Royal Statistical Society, 61, 181–211.

Brownlee, K. A. (1957). The principles of experimental design. Industrial Quality Control, 13, 1–9.

Eisenhart, C. (1947). The assumptions underlying the analysis of variance. Biometrics, 3, 1–21.

Melo, O. O., López, L. A., & Melo, S. E. (2007). Diseño de experimentos: métodos y aplicaciones. Universidad Nacional de Colombia. Facultad de Ciencias.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Diseño de experimentos para la calibración de la heurística de optimización de muros de contrafuertes

Variables geométricas del muro de contrafuertes

En la actualidad, los técnicos se enfrentan al desafío de encontrar soluciones estructurales más eficientes cumpliendo con todas las restricciones de seguridad y funcionalidad. Como ayuda a este reto, surgen las técnicas de optimización heurísticas. El algoritmo aplicado en este artículo es el Recocido Simulado o Simulated Annealing (SA). La estructura sobre la que se emplea esta metodología es un muro de contrafuertes de hormigón armado de 11 metros de altura. La eficiencia del algoritmo depende de la elección de los parámetros más adecuados que lo definen. Para ello, se realiza un diseño de experimentos factorial fraccionado que permite, a través de un análisis estadístico, detectar aquellos parámetros de la heurística que más afectan al resultado de la solución obtenida.

Referencia:

MARTÍ, J.V.; MARTÍNEZ-MUÑOZ, D.; YEPES, V. (2022). Diseño de experimentos para la calibración de la heurística de optimización de muros de contrafuertes. VIII Congreso de la Asociación Española de Ingeniería Estructural ACHE. Santander, 2022, 10 pp.

Pincha aquí para descargar

Cuando una «campaña experimental» se convierte en un desperdicio de tiempo y dinero

https://www.laensa.com/probetas-hormigon/

Reconozco abiertamente que me recorre cierto escalofrío cuando escucho por algún sitio que se está desarrollando una «campaña experimental«, a menudo en laboratorios donde, por desgracia, cada ensayo cuesta muchísimo tiempo y dinero. Me viene a la mente una campaña militar a gran escala donde, para conseguir un objetivo, se sacrifica lo que sea necesario. Cuando igual una pequeña fuerza de operaciones especiales sería suficiente.

Lo digo porque no es la primera vez que me encuentro con algún estudiante de máster o doctorado que quiere iniciar ensayos para cubrir, literalmente, las variaciones posibles en ciertos rangos, de un número de factores que influyen en un problema determinado. Y tampoco me es ajeno el típico estudiante que acude a mi despacho a pedirme consejo porque no sabe qué hacer con las montañas de datos generados, no siendo capaz de interpretar con herramientas estadísticas rigurosas.

Pero este problema no solo ocurre en determinados ámbitos científicos, sino que es habitual en empresas, procesos industriales y laboratorios de todo tipo. Cuento esto porque encuentro de vez en cuando a un doctorando que ha dedicado, por ejemplo, más de cinco años en recoger datos que luego, a la postre, se acumulan en hojas de cálculo y son difíciles de interpretar porque no se sabía exactamente cuál era la pregunta de investigación que se quería resolver.

También es muy típico encontrar en las empresas a técnicos expertos en un proceso determinado «con mucha experiencia», que realmente lo que ha hecho es aprender con los años, y sobre todo, de sufrir en sus carnes muchos errores. Este tipo de experiencia, basada en el error, no es la más barata, ni mucho menos.

Afortunadamente, cada vez son menos los que se enfrascan directamente a ensayar todas las combinaciones posibles en los valores de ciertas variables. Para eso disponemos de una rama del conocimiento denominada diseño de experimentos que permite no solo ahorrar recursos (tiempo, espacio de laboratorio, dinero, etc.), sino también es capaz de sacar muchísima más información de los datos cuando se dedica algo de tiempo a hacer un buen diseño experimental. No digo con esto que existan campañas experimentales bien diseñadas, sino que aún perviven prácticas que, por puro desconocimiento, son utilizadas aún en demasiadas ocasiones.

Veamos un ejemplo sencillo que nos permite aclarar las ideas. Imaginemos un proceso que solo depende de 4 factores. Si de cada factor queremos analizar 5 niveles, una «campaña experimental» exhaustiva nos obligaría a tomar 5^4 = 625 observaciones. Este número tan elevado puede ser inviable. ¿Cómo podemos reducir el número de observaciones? Se podría reducir el número de factores o el número de niveles a estudiar .

Un buen diseño de experimentos puede reducir muchísimo el número de observaciones necesarias ofreciendo, a su vez, información muy valiosa. Por ejemplo, un diseño factorial a dos niveles, ya sea completo o fraccionado, sería suficiente en la mayoría de los casos para estudiar los efectos, las interacciones entre los factores, etc. Invito al lector a revisar en este mismo blog algunos artículos que he escrito al respecto:

¿Qué es el diseño de experimentos?

Definiciones básicas del diseño de experimentos

Incluso, en el caso de que no exista una interacción entre los factores, por ejemplo un diseño en cuadrado grecolatino, para cuatro factores y cuatro niveles, podríamos obtener información valiosa con 16 observaciones en vez de las 256 que serían las necesarias para cubrir todas las combinaciones posibles. En este blog podéis encontrar muchos ejemplos resueltos buscando «diseño de experimentos» en la columna de la izquierda, donde aparece el buscador.

Resumiendo, estoy a favor de las «campañas experimentales», pero siempre que se basen en un diseño de experimentos previo. Pero mi consejo es que antes de hacer nada, tengamos muy clara la pregunta de investigación que queremos resolver. De hecho, la ciencia experimental trata de llegar a conclusiones generales con datos procedentes de casos particulares, y para eso necesitamos la estadística.

Parafraseando la frase que, según la tradición, estaba grabada a la entrada de la Academia de Platón, yo pondría el siguiente letrero a la puerta de cualquier laboratorio: «NO ENTRE NADIE QUE NO SEPA ESTADÍSTICA».

Os dejo una conferencia del profesor Xabier Barber de la Universidad Miguel Hernández que os aclarará muchas cosas. Espero que os guste.

Referencias:

Box, G.E.; Hunter, J.S.; Hunter, W.G. (2008). Estadística para investigadores. Diseño, innovación y descubrimiento. Segunda Edición, Ed. Reverté, Barcelona.
Gutiérrez, H.; de la Vara, R. (2003). Análisis y diseño de experimentos. McGraw-Hill, México.
Vicente, M.L.; Girón, P.; Nieto, C.; Pérez, T. (2005). Diseño de experimentos. Soluciones con SAS y SPSS. Pearson Educación, Madrid.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Diseño de experimentos por bloques aleatorizados. Aplicación al control de calidad del hormigón

Laboratorio de materiales de ICITECH. https://icitech.blogs.upv.es/index.php/home/laboratorio-de-materiales/

En la asignatura de “Modelos predictivos y de optimización de estructuras de hormigón”, del Máster en Ingeniería del Hormigón, se desarrollan laboratorios informáticos. En este caso, os traigo un ejemplo de aplicación de un diseño de experimentos. En este caso, un diseño de experimentos por bloques aleatorizados resuelto con SPSS y MINITAB.

Se pretende comparar la resistencia a compresión simple a 28 días obtenidos por cuatro laboratorios diferentes. Para ello se realizan cinco amasadas diferentes y se obtienen las resistencias medias para cada amasada por cada uno de los laboratorios. Los resultados se encuentran en la tabla que sigue.

Os paso la resolución de este laboratorio informático. Espero que os sea de interés.

Pincha aquí para descargar

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Hormigón compactado con una pavimentadora. Ejemplo de un diseño factorial fraccionado resuelto con MINITAB

https://www.360enconcreto.com/blog/detalle/innovacion-y-tendencias/pavimentos-de-concreto-compactados-con-rodillo

En la asignatura de «Modelos predictivos y de optimización de estructuras de hormigón», del Máster en Ingeniería del Hormigón, se desarrollan laboratorios informáticos. En este caso, os traigo un ejemplo de aplicación de un diseño de experimentos. En este caso, un diseño factorial fraccionado resuelto con MINITAB.

Se quiere determinar la mejor forma de elaborar hormigón compactado con una pavimentadora. La variable de respuesta es el porcentaje de compactación, medido con un densímetro nuclear. Tras una tormenta de ideas con expertos, se ha realizado un diseño de experimentos con 5 factores: el porcentaje de aditivo, la pavimentadora (A antigua, B moderna), el operador de la pavimentadora (A con poca experiencia, y B con mucha), el tipo de mezcla de hormigón y la temperatura del hormigón. Se ha tenido que realizar un diseño fraccionado puesto que el presupuesto limita el número de experimentos a un máximo de 12. Se pide que se analicen los resultados, que fueron los de la tabla siguiente:

Los datos de este caso provienen de la siguiente publicación: Arias, C.; Adanaqué, I.; Buestán, M. Optimización del proceso de elaboración de hormigón compactado con pavimentadora. Escuela Superior Politécnica del Litoral, Ecuador. http://www.dspace.espol.edu.ec/handle/123456789/4754

Os paso la resolución de este laboratorio informático. Espero que os sea de interés.

Pincha aquí para descargar

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Aplicación de la metodología de la superficie de respuesta en un curso de postgrado de optimización

Este trabajo describe la introducción de la metodología de superficie de respuesta en un curso de postgrado. Este caso se realiza en la asignatura de «Modelos predictivos y de optimización de estructuras de hormigón«. Esta asignatura se enmarca en el Plan de Estudios del Máster Universitario en Ingeniería del Hormigón. Los estudiantes aprenden aquí conceptos como la optimización de estructuras mediante algoritmos heurísticos, la toma de decisiones multicriterio, técnicas de diseño de experimentos y metamodelos como la superficie de respuesta para obtener resultados óptimos. En este caso de estudio, el objetivo es obtener una solución óptima de un muro de hormigón armado, utilizando las emisiones de CO2 como función objetivo para reducir su impacto. Para aplicar esta metodología, los estudiantes aprovechan programas comerciales. Por un lado, para realizar el análisis estadístico que permita obtener la superficie de respuesta se utiliza Minitab. Por otro lado, los estudiantes comprueban la resistencia de la estructura utilizando el software de cálculo estructural Cype. Como resultado de esta metodología se consigue que los estudiantes alcancen un mejor nivel en competencias transversales, como el diseño y el proyecto, el pensamiento crítico, el análisis y la resolución de problemas o el uso de software específico. En este trabajo se presentan futuros estudios de investigación relacionados con el uso de técnicas de optimización de estructuras por parte de los estudiantes aplicando otras técnicas de optimización diferentes.

Referencia:

YEPES, V.; MARTÍNEZ-MUÑOZ, D.; MARTÍ, J.V. (2021). Application of the response surface methodology in a postgraduate optimization course. 15th annual International Technology, Education and Development Conference (INTED 2021), 8th-9th March, 2021, pp. 869-878, Valencia, Spain. ISBN: 978-84-09-27666-0

Pincha aquí para descargar

Diseño de experimentos en cuadrado grecolatino. Ejemplo aplicado al hormigón

Figura 1. Cuadrado grecolatino de orden cuatro. Wikipedia

Un cuadrado greco-latino, cuadrado de Euler o cuadrados latinos ortogonales de orden n se denomina, en matemáticas, a la disposición en una cuadrícula cuadrada n×n de los elementos de dos conjuntos S y T, ambos con n elementos, cada celda conteniendo un par ordenado (s, t), siendo s elemento de S y t de T, de forma que cada elemento de S y cada elemento de T aparezca exactamente una vez en cada fila y en cada columna y que no haya dos celdas conteniendo el mismo par ordenado. Si bien los cuadrados grecolatinos eran una curiosidad matemática, a mediados del siglo XX Fisher demostró su utilidad para el control de experimentos estadísticos.

El diseño de experimentos en cuadrado grecolatino constituye una extensión del cuadrado latino. En este caso se eliminan tres fuentes extrañas de variabilidad, es decir, se controlan tres factores de bloques y un factor de tratamiento. Se trata de un diseño basado en una matriz de «n» letras latinas y «n» letras griegas, de forma que cada letra latina aparece solo una vez al lado de cada letra griega. Lo interesante de este diseño es que se permite la investigación de cuatro factores (filas, columnas, letras latinas y letras griegas), cada una con «n» niveles en solo «n²» corridas. Se llama cuadrado grecolatino porque los cuatro factores involucrados se prueban en la misma cantidad de niveles, de aquí que se pueda escribir como un cuadro. En la Figura 1 se presenta el aspecto de los datos del diseño de orden cuatro. El inconveniente de este modelo es que su utilización es muy restrictiva. El análisis de la varianza permite comprobar las hipótesis de igualdad de letras latinas (tratamientos), de las filas, de las columnas y de las letras griegas.

Si a un cuadrado latino p x p se le superpone un segundo cuadrado latino n x n en el que los tratamientos se denotan con letras griegas, entonces los dos cuadrados tienen la propiedad de que cada letra griega aparece una y sólo una vez con cada letra latina. Este diseño permite controlar sistemáticamente tres fuentes de variabilidad extraña. Ello permite la investigación de cuatro factores (filas, columnas, letras latinas y letras griegas), cada una con p niveles en sólo n² ensayos.

Por tanto, el diseño de experimentos en cuadrado grecolatino se caracteriza por lo siguiente:

Es un diseño con cuatro factores a n niveles
Se asume que no hay interacciones entre los factores
Requiere de n² observaciones
Cada nivel de un factor aparece una vez con cada nivel de los otros factores
Se trata de la superposición de dos cuadrados latinos (ver Figura 2)

Figura 2. Superposición de dos cuadrados latinos

En un diseño en cuadrado greco-latino la variable respuesta y_ij(hp) viene descrita por la siguiente ecuación:

A continuación os presento un caso para aclarar la aplicabilidad de este diseño de experimentos. Se trata de averiguar si la resistencia característica del hormigón a flexocompresión (MPa) varía con cuatro dosificaciones diferentes. Para ello se han preparado amasadas en cuatro amasadoras diferentes, se han utilizado cuatro operarios de amasadora y los ensayos se han realizado en cuatro laboratorios diferentes. Los resultados se encuentran en la tabla que sigue. Se quiere analizar el diseño de experimentos en cuadrado grecolatino realizado.

En el caso que nos ocupa, la variable de respuesta de la resistencia característica del hormigón a flexocompresión (MPa). El factor que se quiere estudiar es la dosificación a cuatro niveles (A, B, C y D). El bloque I es el tipo de amasadora, con cuatro niveles (α, β, γ y δ). El bloque II es el operario de la amasadora, con cuatro niveles (1, 2, 3 y 4). El bloque III es el laboratorio, con cuatro niveles (las filas). Se supone que no hay interacción entre el factor y los bloques entre sí.

Lo que se quiere averiguar es si hay diferencias significativas entre las dosificaciones (el factor a estudiar). De paso, se desea saber si hay diferencias entre los laboratorios, los operarios y las amasadoras (los bloques).

Os paso un pequeño vídeo donde se explica, de forma muy resumida, este caso, tanto para SPSS como para MINITAB.

Os dejo otro vídeo donde también se explica este tipo de diseño de experimentos.

Referencias:

Gutiérrez, H.; de la Vara, R. (2004). Análisis y Diseño de Experimentos. McGraw Hill, México.
Vicente, MªL.; Girón, P.; Nieto, C.; Pérez, T. (2005). Diseño de Experimentos. Soluciones con SAS y SPSS. Pearson, Prentice Hall, Madrid.
Pérez, C. (2013). Diseño de Experimentos. Técnicas y Herramientas. Garceta Grupo Editorial, Madrid.

Diseño de experimentos factorial completo aplicado al proyecto de muros de contención

En el congreso CMMoST 2019 (5th International Conference on Mechanical Models in Structural Engineering), celebrado en Alicante del 23 al 25 de octubre de 2019, tuvimos la ocasión de presentar varias comunicaciones. A continuación os paso una denominada “Diseño de experimentos factorial completo aplicado al proyecto de muros de contención“.

En este caso, se trataba aplicar una técnica estadística procedente del diseño de experimentos, el diseño factorial completo, para determinar las variables significativas y las interacciones entre las variables cuando se trata de calcular una estructura. En este caso, se trata de analizar las emisiones de CO2 en la construcción de un muro de contención de tierras. Esta metodología es muy interesante para los estudiantes de máster. Ya hemos publicado algún artículo sobre el mismo tema aplicado a puentes pretensados. Os dejo el artículo en abierto.

Referencia:

MARTÍNEZ-MUÑOZ, D.; YEPES, V.; MARTÍ, J.V. (2019). Diseño de experimentos factorial completo aplicado al proyecto de muros de contención. 5th International Conference on Mechanical Models in Structural Engineering, CMMoST 2019, 23-25 oct 2019, Alicante, Spain, pp. 201-213. ISBN: 978–84–17924–58–4

Pincha aquí para descargar

Optimización de muros de hormigón mediante la metodología de la superficie de respuesta

En el congreso CMMoST 2019 (5th International Conference on Mechanical Models in Structural Engineering), celebrado en Alicante del 23 al 25 de octubre de 2019, tuvimos la ocasión de presentar varias comunicaciones. A continuación os paso una denominada «Optimización de muros de hormigón mediante la metodología de la superficie de respuesta«.

En este caso, se trataba aplicar una técnica estadística procedente del diseño de experimentos, la metodología de la superficie de respuesta, a un cálculo estructural, en este caso, un muro. La optimización de procesos mediante la superficie de respuesta es habitual en el campo de la experimentación. La idea es considerar que el cálculo de una estructura se puede considerar también un experimento, donde los datos de entrada son las variables y parámetros que definen dicha estructura y el resultado final es el coste. En este caso, se trata de minimizar el coste. Esta metodología es muy interesante para los estudiantes de máster. Ya hemos publicado algún artículo sobre el mismo tema aplicado a puentes pretensados. Os dejo el artículo en abierto. En este caso se han optimizado las emisiones de CO2.

Referencia:

YEPES, V.; MARTÍNEZ-MUÑOZ, D.; MARTÍ, J.V. (2019). Optimización de muros de hormigón mediante la metodología de la superficie de respuesta. 5th International Conference on Mechanical Models in Structural Engineering, CMMoST 2019, 23-25 oct 2019, Alicante, Spain, pp. 603-615. ISBN: 978–84–17924–58–4

Pincha aquí para descargar