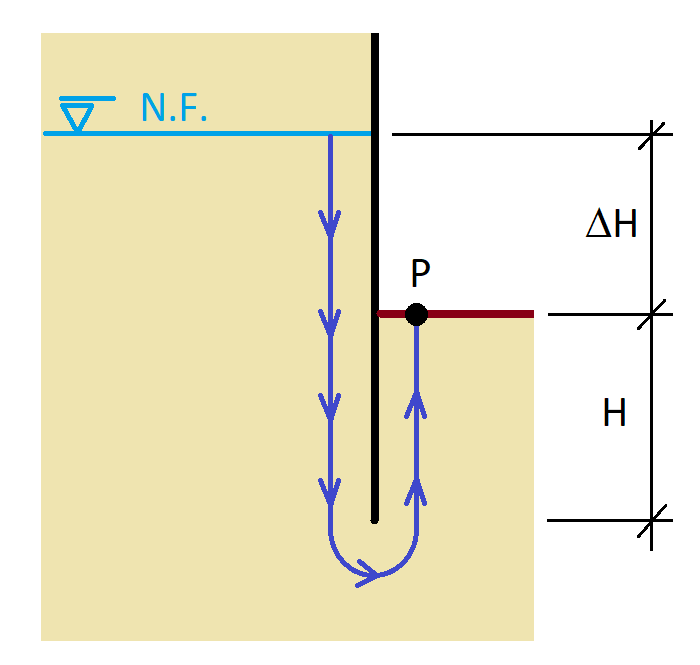
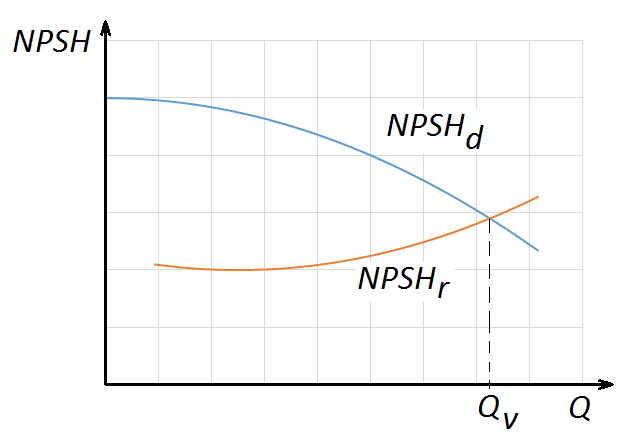
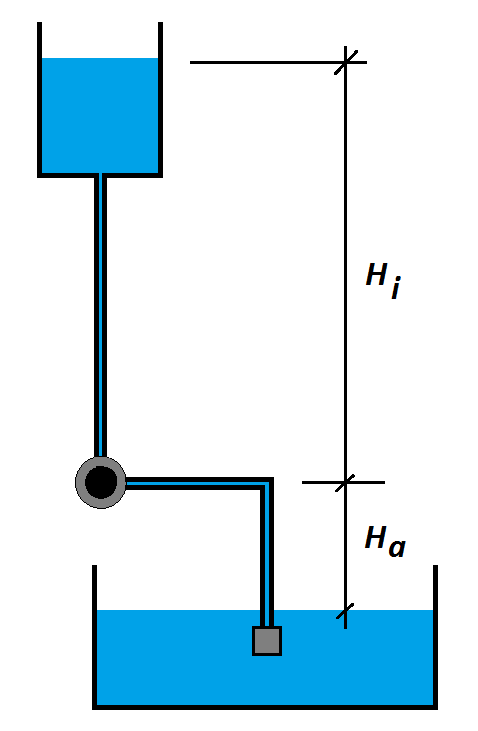
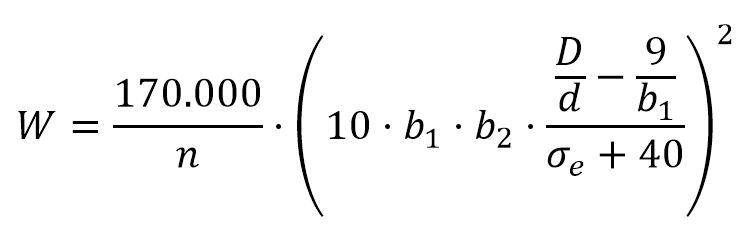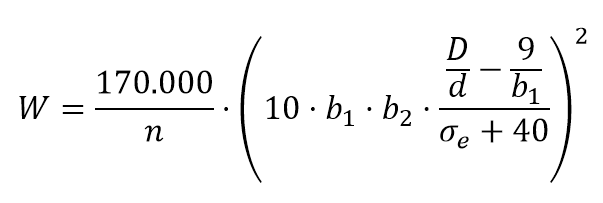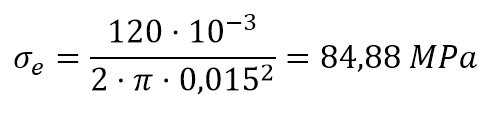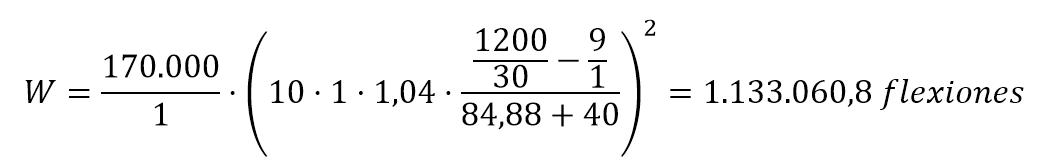 Cuando se trata de seleccionar una bomba adecuada para impulsar un fluido, no solo debemos conocer la altura de impulsión y el caudal que queremos elevar, sino que se debe evitar el fenómeno de la cavitación. Para ello, uno de los conceptos básicos es conocer la altura neta positiva de aspiración NPSH requerida de la bomba en cada condición de capacidad de operación y carga total, que deberá ser menor a la disponible. De este tema ya hemos hablado en algún artículo anterior.
Cuando se trata de seleccionar una bomba adecuada para impulsar un fluido, no solo debemos conocer la altura de impulsión y el caudal que queremos elevar, sino que se debe evitar el fenómeno de la cavitación. Para ello, uno de los conceptos básicos es conocer la altura neta positiva de aspiración NPSH requerida de la bomba en cada condición de capacidad de operación y carga total, que deberá ser menor a la disponible. De este tema ya hemos hablado en algún artículo anterior.
Para aclarar un poco más estos conceptos, os dejo un vídeo explicativo y un problema resuelto para el caso de una instalación en aspiración. En este problema, se ha optado por calcular las pérdidas por fricción usando las tablas aportadas por una casa comercial.
Este es uno de los casos estudiados en el “Curso de procedimientos de contención y control del agua subterránea en obras de Ingeniería Civil y Edificación”. Espero que os sea de interés.
Referencias:
- DÍAZ DEL RÍO, M. (2007). Maquinaria de construcción. 2ª edición. McGraw-Hill/Interamericana de España, S.A., 944 pp.
- IDEA (2012). Guía técnica de selección de equipos de transporte de fluidos. Asociación Técnica Española de Climatización y Refrigeración, Madrid, 108 pp.
- ŁUSZCZEWSKI, A. (1999). Redes industriales de tubería. Bombas para agua, ventiladores y compresores. Diseño y construcción. Reverté Ediciones. México. 302 pp.
- YEPES, V. (2020). Procedimientos de construcción de cimentaciones y estructuras de contención. Colección Manual de Referencia, 2ª edición. Editorial Universitat Politècnica de València, 480 pp. Ref. 328. ISBN: 978-84-9048-903-1.
- YEPES, V.; MARTÍ, J.V. (2017). Máquinas, cables y grúas empleados en la construcción. Editorial de la Universitat Politècnica de València. Ref. 814. Valencia, 210 pp.
- YEPES, V. (2023). Maquinaria y procedimientos de construcción. Problemas resueltos. Colección Académica. Editorial Universitat Politècnica de València, 562 pp. Ref. 376. ISBN 978-84-1396-174-3