La trascendencia económica del sector del transporte genera costos sociales y medioambientales de gran envergadura. Esta actividad supone aproximadamente un sexto del Producto Interno Bruto (PIB) de los países industrializados (ver Yepes, 2002). Un estudio del National Council of Physical Distribution (ver Ballou, 1991) estima que el transporte sumó un 15% del PIB de Estados Unidos en 1978, constituyendo más del 45% de todos los costos logísticos de las organizaciones. En España, según datos del Ministerio de Fomento (ver CTCICCP, 2001), la participación del sector en el valor añadido bruto del año 1997 se situó en un 4.6%. En cuanto al empleo, 613,400 personas se encontraban ocupadas en el año 1999 en el sector de transportes en España, lo cual representa el 3.69% de la población activa. La distribución física representa para las empresas entre la sexta y la cuarta parte de las ventas y entre uno y dos tercios del total de los costos logísticos (Ballou, 1991). Continue reading «Optimización económica de redes de transporte»→
¿Cómo se podrían optimizar en tiempos de cálculo razonable problemas complejos de redes de transporte, estructuras de hormigón (puentes, pórticos de edificación, túneles, etc.) y otro tipo de problemas de decisión empresarial cuando la dimensión del problema es de tal calibre que es imposible hacerlo con métodos matemáticos exactos? La respuesta son los métodos aproximados, también denominados heurísticas. Este artículo divulgativo trata de ampliar otros anteriores donde ya hablamos de los algoritmos, de la optimización combinatoria, de los modelos matemáticos y otros temas similares. Para más adelante explicaremos otros temas relacionados específicamente con aplicaciones a problemas reales. Aunque para los más curiosos, os paso en abierto, una publicación donde se han optimizado con éxito algunas estructuras de hormigón como muros, pórticos o marcos de carretera: (González et al, 2008).
Desde los primeros años de la década de los 80, la investigación de los problemas de optimización combinatoria se centra en el diseño de estrategias generales que sirvan para guiar a las heurísticas. Se les ha llamado metaheurísticas. Se trata de combinar inteligentemente diversas técnicas para explorar el espacio de soluciones. Osman y Kelly (1996) nos aportan la siguiente definición: “Los procedimientos metaheurísticos son una clase de métodos aproximados que están diseñados para resolver problemas difíciles de optimización combinatoria, en los que los heurísticos clásicos no son ni efectivos ni eficientes. Los metaheurísticos proporcionan un marco general para crear nuevos algoritmos híbridos combinando diferentes conceptos derivados de la inteligencia artificial, la evolución biológica y la mecánica estadística”.
Aunque existen diferencias apreciables entre los distintos métodos desarrollados hasta el momento, todos ellos tratan de conjugar en mayor o menor medida la intensificación en la búsqueda –seleccionando movimientos que mejoren la valoración de la función objetivo-, y la diversificación –aceptando aquellas otras soluciones que, aun siendo peores, permiten la evasión de los óptimos locales-.
Las metaheurísticas son susceptibles de agruparse de varias formas. Algunas clasificaciones recurren a cambios sucesivos de una solución a otra en la búsqueda del óptimo, mientras otras se sirven de los movimientos aplicados a toda una población de soluciones. El empleo, en su caso, de memoria que guíe de la exploración del espacio de elecciones posibles permite otro tipo de agrupamiento. En otras circunstancias se emplean perturbaciones de las opciones, de la topología del espacio de soluciones, o de la función objetivo. En la Figura se recoge una propuesta de clasificación de las heurísticas y metaheurísticas empleadas en la optimización combinatoria (Yepes, 2002), teniendo en común todas ellas la necesidad de contar con soluciones iniciales que permitan cambios para alcanzar otras mejores. Es evidente que existen en este momento muchas más técnicas de optimización, pero puede ser dicha clasificación un punto de partida para una mejor taxonomía de las mismas.
Figura. Taxonomía de estrategias empleadas en la resolución aproximada de problemas de optimización combinatoria sobre la base de soluciones iniciales (Yepes, 2002)
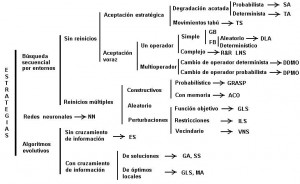
Las metaheurísticas empleadas en la optimización combinatoria en podrían clasificarse en tres grandes conjuntos. Las primeras generalizan la búsqueda secuencial por entornos de modo que, una vez se ha emprendido el proceso, se recorre una trayectoria de una solución a otra vecina hasta que éste concluye. En el segundo grupo se incluyen los procedimientos que actúan sobre poblaciones de soluciones, evolucionando hacia generaciones de mayor calidad. El tercero lo constituyen las redes neuronales artificiales. Esta clasificación sería insuficiente para aquellas metaheurísticas híbridas que emplean, en mayor o menor medida, estrategias de unos grupos y otros. Esta eventualidad genera un enriquecimiento deseable de posibilidades adaptables, en su caso, a los diferentes problemas de optimización combinatoria.
Referencias
GONZÁLEZ-VIDOSA-VIDOSA, F.; YEPES, V.; ALCALÁ, J.; CARRERA, M.; PEREA, C.; PAYÁ-ZAFORTEZA, I. (2008) Optimization of Reinforced Concrete Structures by Simulated Annealing. TAN, C.M. (ed): Simulated Annealing. I-Tech Education and Publishing, Vienna, pp. 307-320. (link)
YEPES, V. (2002). Optimización heurística económica aplicada a las redes de transporte del tipo VRPTW. Tesis Doctoral. Escuela Técnica Superior de Ingenieros de Caminos, Canales y Puertos. Universitat Politècnica de València. 352 pp. ISBN: 0-493-91360-2. (pdf)
Cuando se trata de construir un puente con vigas prefabricadas, uno de los problemas a resolver es el transporte por carretera de dichos elementos. Debido a las características técnicas de la carga, que exceden en dimensiones, masa y carga por eje las máximas autorizadas, se requiere una Autorización Complementaria de Circulación que expedirá el Organismo competente en materia de tráfico. Las unidades de transporte son camiones semirremolques, habitualmente denominados «dollys».
A continuación, os paso varios vídeos explicativos y un vídeo tutorial de Javier Luque en el que se aplica el concepto de Centro Instantáneo de Rotación para el cálculo de velocidades lineales en función de los condicionantes iniciales de la velocidad angular. Un buen problema de física que se aplica al transporte de vigas de gran tamaño. Espero que os sean útiles los vídeos.
La investigación de operaciones, o investigación operativa, es una rama de las matemáticas que consiste en el uso de modelos matemáticos, estadística y algoritmos con objeto de modelar y resolver problemas complejos , determinando la solución óptima y permitiendo, de este modo, tomar decisiones. Frecuentemente, se trata del estudio de complejos sistemas reales, con la finalidad de mejorar (u optimizar) su funcionamiento. La investigación de operaciones permite el análisis de la toma de decisiones teniendo en cuenta la escasez de recursos, para determinar cómo se puede optimizar un objetivo definido, como la maximización de los beneficios o la minimización de costos.
Aunque su nacimiento como ciencia se establece durante la Segunda Guerra Mundial y debe su nombre a las operaciones militares, los verdaderos orígenes de la Investigación Operativa se remontan mucho más atrás en el tiempo, hasta el siglo XVII. Esta disciplina nació en Inglaterra durante la Segunda Guerra Mundial como estrategia para encontrar soluciones a problemas militares, lo cual requirió crear un Grupo de Investigación de Operaciones Militares compuesto por científicos multidisciplinares. Al terminar la guerra, este método se empleó para resolver problemas generales como el control de inventarios, la asignación de recursos y las líneas de espera, entre otros. Esta técnica cumplió sus objetivos en las décadas de los cincuenta y sesenta, hasta su pleno desarrollo en la actualidad. Sin embargo, su auge se debe en gran medida al desarrollo de la informática, gracias a la cual es posible resolver problemas y obtener soluciones que, de otra forma, conllevarían un enorme tiempo de cálculo. Debido a su éxito, la investigación operativa se extendió a otros campos, como la industria, la física, la informática, la economía, la estadística y la probabilidad, la ecología, la educación, el servicio social, entre otros, y actualmente se utiliza prácticamente en todas las áreas. Algunos de los promotores más importantes de la filosofía y la aplicación de la investigación de operaciones son C.W. Entre ellos se encuentran Churchman, R. L. Ackoff y R. Bellman. Actualmente, la investigación operativa incluye una gran cantidad de ramas, como la programación lineal, la programación no lineal, la programación dinámica, la simulación, la teoría de colas, la teoría de inventarios, la teoría de grafos, etc.
Os presento ahora un vídeo sobre el tema que no llega a 3 minutos de duración. Espero que os guste.
Empezamos una serie de artículos que tratarán aspectos relacionados con el transporte, la logística, la distribución de mercancías, la investigación de operaciones y, en definitiva, la toma de decisiones en las empresas. Como siempre, el objeto es divulgativo, abriendo puertas a la reflexión y no pretendiendo, ni mucho menos, abarcar todos los aspectos de un tema determinado. Empezamos, pues.
El National Council of Physical Distribution Management definió, en 1979 (ver Ballou, 1991), la gestión de la distribución física como “todas aquellas actividades encaminadas a la planificación, implementación y control de un flujo creciente de materias primas, recursos de producción y productos finales desde el punto de origen hasta el de consumo”. Entre estas tareas se encuentran el servicio al cliente, la previsión de la demanda, el control de inventarios, los servicios de reparación, el manejo de mercancías, el procesamiento de pedidos, la selección de la ubicación geográfica de las fábricas y los almacenes, las compras, el empaquetado de productos, el tratamiento de las mercancías devueltas, la recuperación y tratamiento de desperdicios, la distribución y el transporte, y el almacenamiento. Sin embargo, otros autores prefieren emplear el término logística empresarial.
La importancia de la eficacia y la eficiencia en la gestión de la distribución adquiere su verdadera magnitud cuando se consideran los costes. Kotler (1991) indica que los principales elementos de los costes de la distribución física son el transporte (37%), el control de existencias (22%), el almacenamiento (21%) y otros como la recepción de órdenes, el servicio al cliente, la distribución y la administración (20%). El mismo autor cree, al igual que otros expertos, que pueden conseguirse ahorros sustanciales en el área de la distribución física, la cual ha sido descrita como “la última frontera para obtener economías en los costes” y “el continente oscuro de la economía”. Drucker (1962) describió las actividades logísticas que se llevaban a cabo tras la fabricación como las “áreas peor realizadas y, a la vez, más prometedoras dentro del mundo industrial”.
Muchas empresas sostienen que el objetivo último de la distribución física es obtener las mercancías necesarias, llevarlas a los lugares oportunos a su debido tiempo y a un coste lo más bajo posible. Sin embargo, tal como afirma Kotler (1991), no existe ningún sistema de distribución que pueda, simultáneamente, maximizar el servicio al cliente y minimizar los costes de distribución, puesto que lo primero conlleva un elevado coste de existencias, un transporte rápido y múltiples almacenes, factores que incrementan los costes. Se trata de buscar un equilibrio que concilie los intereses contrapuestos.
La gestión de la distribución física presenta una amplia variedad de problemas de decisión que inciden en la planificación en los ámbitos estratégico, táctico y operativo. La localización de plantas y almacenes, o la reconfiguración de la red de transporte, son decisiones estratégicas, mientras que los problemas relacionados con la dimensión de la flota, o con si esta debe ser propia o alquilada, pertenecen al ámbito de las decisiones tácticas. Los problemas habituales en las operaciones son: (a) el establecimiento de rutas para vehículos que, con cierta limitación de capacidad, deben distribuir o recoger mercancías a un grupo de clientes; y (b) la programación de horarios o precedencias entre destinos para satisfacer estos recorridos.
Un estudio del National Council of Physical Distribution (ver Ballou, 1991) estima que el transporte representó el 15% del Producto Interior Bruto de Estados Unidos en 1978, lo que supuso más del 45% de todos los costes logísticos de las organizaciones. El sector de las empresas de servicios públicos y de transporte estadounidenses movió en 1991 aproximadamente 506 millardos de dólares, según el Informe del Presidente de 1994 (ver Fisher, 1997). King y Mast (1997) señalan que la valoración anual de los excesos de coste de los viajes en Estados Unidos asciende a 45 millardos de dólares. En el Reino Unido, Francia y Dinamarca, por ejemplo, el transporte representa cerca del 15%, 9% y 15% del gasto nacional, respectivamente (Crainic y Laporte, 1997; Larsen, 1999). En Japón, los costes logísticos suponen un 26,5% de las ventas y los de transporte, un 13,5% (Kobayashi, 1973). Estas mismas cifras son del 14,1% y 2,5% en Australia (Stephenson, 1975) y del 16% y 5,5% en el Reino Unido (Murphy, 1972). En España, según datos del Ministerio de Fomento (ver CTCICCP, 2001), la participación del sector transporte en el valor añadido bruto del año 1997 se situó en un 4,6%. En cuanto al empleo, 613.400 personas se encontraban ocupadas en el año 1999 en el sector del transporte público en nuestro país, lo cual supone el 3,69% de la población activa.
Existe una gran variación en los costes logísticos entre las distintas empresas. Ballou (1991) indica que estas cifras oscilan entre menos del 4% sobre las ventas en aquellas empresas que producen y distribuyen mercancías de alto valor y más del 32% en aquellas otras que lo hacen en las de bajo valor. El mismo autor señala que los costes de transporte representan entre una tercera y dos terceras partes del total de costes logísticos. Se estima que los costes de distribución representan casi la mitad del total de costes logísticos en algunas industrias y que en las de alimentación y bebidas pueden incrementar en un 70% el coste de las mercancías (De Backer et al., 1997; Golden y Wasil, 1987). Además, la importancia de la programación de rutas se manifiesta claramente con el dato aportado por Halse (1992), informando que en 1989, el 76,5% de todo el transporte de mercancías se realizó con vehículos.
Así, las actividades que conforman la planificación operativa de la distribución física implican un gran número de pequeñas decisiones interrelacionadas. Además, el número de planes posibles crece exponencialmente con la dimensión del problema. Incluso para flotas pequeñas y con un número moderado de peticiones de transporte, la planificación es una tarea altamente compleja. Por tanto, no es de extrañar que los responsables de estos asuntos simplifiquen al máximo los problemas y utilicen procedimientos particulares para despachar sus vehículos basándose, en multitud de ocasiones, en la experiencia de errores anteriores. Existe un amplio potencial de mejora claramente rentable para las unidades de negocio.
La planificación y la gestión de las redes de distribución exigen la disponibilidad de técnicas eficientes de optimización de rutas, puesto que no solo afectan al desarrollo de las operaciones, sino que también inciden en las decisiones tácticas y estratégicas (tamaño óptimo de flota, estimación de costes, políticas de publicidad y rotura de servicio, etc.).
Medina y Yepes (2000) proporcionan un ejemplo práctico que muestra cómo la aplicación de técnicas de optimización condiciona críticamente el desarrollo de ciertas operaciones de distribución. Se trata de un negocio de venta de paquetes turísticos con transporte incluido; donde los precios se fijan mucho antes de que la demanda sea conocida, y donde son frecuentes las cancelaciones de última hora así como la llegada de nuevos clientes. Si el número de pasajeros es pequeño, en comparación con la máxima capacidad de carga del vehículo, los beneficios o las pérdidas generadas por el transporte dependen fuertemente de la eficiencia del sistema de optimización de rutas. La siguiente figura describe la influencia de la optimización de operaciones en la planificación y la gestión de redes de distribución de baja demanda.
Planificación y gestión de redes de distribución. Fuente: Medina y Yepes (2000).
En apretada síntesis, la planificación y la gestión de las redes de distribución generan una gran variedad de problemas de decisión, cuyo éxito depende críticamente de la optimización de las operaciones, en las que el espectro de soluciones posibles es enorme y, además, creciente exponencialmente con el número de destinos y el tamaño de la flota. Esta explosión combinatoria de soluciones y la complejidad de las variables impiden que la optimización sea, en muchas situaciones reales, abordable mediante técnicas de resolución exactas. Afortunadamente, existen procedimientos alternativos que, si bien no garantizan la solución óptima, sí ofrecen soluciones de calidad para los problemas cotidianos.
De esta forma, la resolución de los problemas de distribución se convierte en una de las parcelas notables de la Investigación Operativa. Incluso el recorte de una pequeña fracción de los costes puede generar enormes ahorros económicos y reducir los impactos medioambientales ocasionados por la polución y el ruido, además de incrementar significativamente la satisfacción de los requerimientos de los clientes.
Referencias
BACKER DE, B.; FURNON, V.; PROSSER, P.; KILBY, P.; SHAW, P.(1997). Local Search in Constraint Programming: Application to the Vehicle Routing Problem. Presented at the CP-97 Workshop on Industrial Constraint-based Scheduling, Schloss Hagenberg, Austria.
BALLOU, R.H. (1991). Logística empresarial. Control y planificación. Ed. Díaz de Santos, Madrid. 655 pp.
COMISIÓN DE TRANSPORTES DEL COLEGIO DE INGENIEROS DE CAMINOS, CANALES Y PUERTOS (2001). Libro Verde del Transporte en España. Disponible en internet. 111 pp.
CRAINIC, T.G.; LAPORTE, G. (1997). Planning Models for Freight Transportation. European Journal of Operational Research, 97: 409-438.
DRUCKER, P. (1962). The Economy’s Dark Continent. Fortune, April: 265-270.
GOLDEN, B.L.; WASIL, E.A. (1987). Computerized Vehicle Routing in the Soft Drink Industry. Operations Research, 35: 6-17.
HALSE, K. (1992). Modeling and Solving complex Vehicle Routing Problems. PhD thesis, Department for Mathematical Modelling, Technical University of Denmark, Lyngby, Denmark.
KING, G.F.; MAST, C.F. (1997). Excess Travel: Causes, Extent and Consequences. Transportation Research Record, 1111: 126-134.
KOBAYASHI, I. (1973). Management of Physical Distribution Cost. Proceedings of International Distribution Conference, Tokyo.
KOTLER, P. (1991). Marketing Management. Analysis, Planning, Implementation, and Control. Prentice Hall International. United Kingdom.
FISHER, M.L. (1997). Vehicle routing. In BALL, M.O.; MAGNANTI, T.L.; MONMA, C.L.; NEMHAUSER, G.L. (Eds.), Network Routing, volume 8 of Handbooks in Operations Research and Management Science, chapter 1, 1-79. North-Holland.
MEDINA, J.R.; YEPES, V. (2000). Optimización de redes de distribución con algoritmos genéticos, en Colomer, J.V. y García, A. (Eds.): Calidad e innovación en los transportes. Actas del IV Congreso de Ingeniería del Transporte. Vol. 1, pp. 205-213. Valencia.
MURPHY, G.J. (1972). Transport and Distribution. Business Books. London.
STEPHENSON, A.R. (1975). Productivity Promotion Council of Australia: 7-10.
YEPES, V. (2002). Optimización heurística económica aplicada a las redes de transporte del tipo VRPTW. Tesis Doctoral. Escuela Técnica Superior de Ingenieros de Caminos, Canales y Puertos. Universidad Politécnica de Valencia. 352 pp.
Trascendencia del transporte
