Las técnicas de programación de proyectos basadas en el cálculo de redes se explican normalmente en los grados de ingeniería civil. Los estudiantes automatizan el cálculo de estas redes de forma sencilla, tanto en el caso de las redes de flechas como en el de las redes de precedencias. Sin embargo, muchas veces no comprenden o les resulta confuso la idea de holgura de un suceso o de una actividad. Incluso en algunos libros de texto confunden los conceptos. Quiero en este artículo aclarar mediante un ejemplo dónde están los problemas asociados al cálculo de las holguras.
Por cierto, podéis repasar en cálculo de una red de flechas o una red de precedencias en alguno de los artículos y vídeos que grabé en su momento. Basta que pulséis el enlace correspondiente.
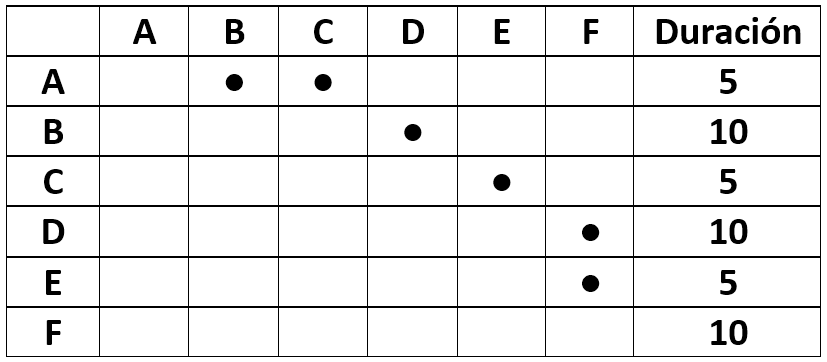
Sea un proyecto compuesto por seis actividades cuyas relaciones de precedencia y duración se muestran en la Tabla 1. En dicha tabla, una actividad situada en una línea precede a la actividad de una columna si la casilla se encuentra marcada. Así, por ejemplo, la actividad A precede tanto a la actividad B como a la C. Para simplificar, las relaciones son final-principio, es decir, la actividad subsecuente no puede iniciarse hasta que se hayan terminado las actividades que le preceden.
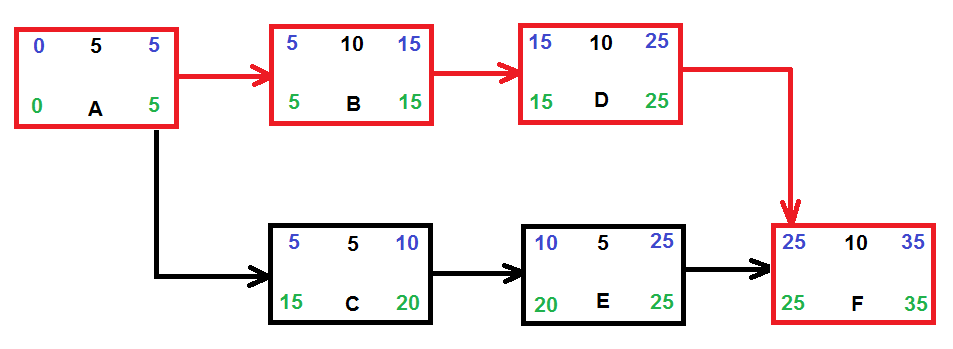
Es fácil representar y calcular el diagrama de flechas correspondiente. Este proyecto tiene un plazo de 35 etapas, siendo el camino crítico el representado por las actividades A, B, D y F (ver Figura 2).

Este mismo proyecto se podría haber calculado usando un diagrama de precedencias, cuya resolución puede verse en la Figura 3. Observe que las fechas más tempranas de inicio de cada actividad tienen un color azul, mientras que las más tardías están en verde. Estas fechas se pueden ver también en la Figura 2.
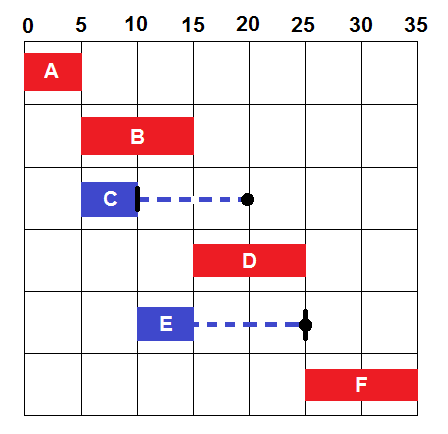
Si representamos el proyecto en un diagrama de barras, se obtiene la Figura 4. Se observa que en este diagrama se ha representado el inicio de cada actividad lo antes posible. Además, se han dibujado la holgura total y libre, separadas ambas por una línea vertical. La actividad C no tiene holgura libre, mientras que en la actividad E, la holgura total y libre coinciden.
Pues veamos ahora dónde están los problemas con las holguras. Previamente, vamos a definir la holgura de una actividad como la diferencia entre el tiempo disponible para realizarla y su duración.
Las holguras se definen en función de los nodos de entrada y salida de la actividad, según se representa en la Figura 5. Existen cinco tipos de holgura: total, libre, independiente, condicional e interferente. Esta última es la diferencia entre la holgura total y la holgura libre.
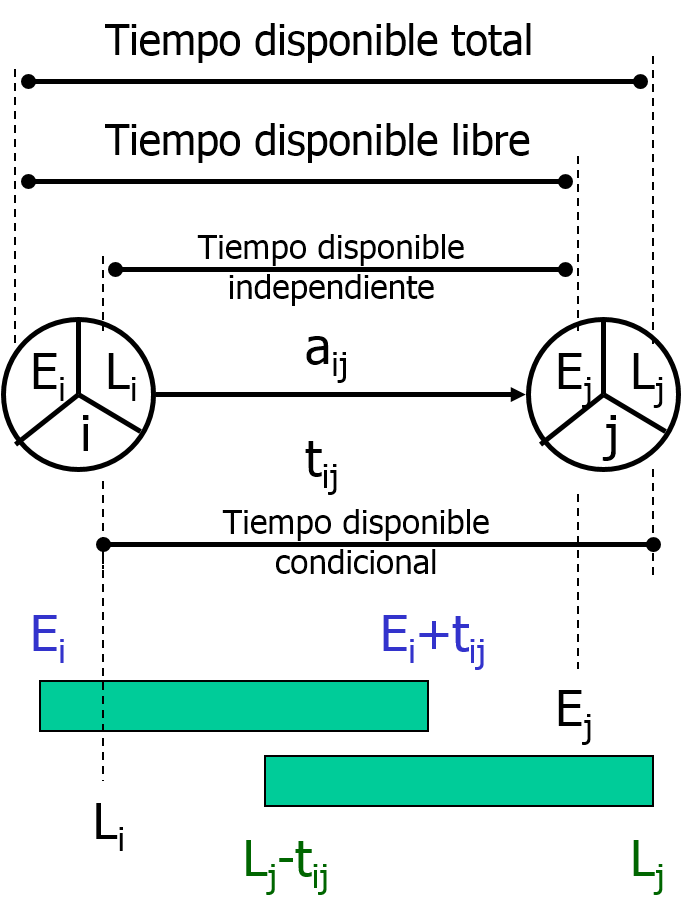
El primer error conceptual que se comete es definir las fechas de los nodos de entrada y salida de una actividad como las fechas más tempranas y tardías de inicio o terminación de dicha actividad. Solo Ei y Lj son la fecha más temprana de inicio y la más tardía de finalización de la actividad. Las fechas Li y Ej corresponden a los nodos correspondientes. En efecto, la fecha más tardía de inicio sería Lj -tij; mientras que la fecha más temprana de terminación sería Ei+tij. Se pueden ver ambas fechas en las barras verdes de la Figura 5. Únicamente en el caso de las fechas representadas dentro de la caja de la actividad de un diagrama de precedencias, tenemos las fechas más tempranas y tardías de inicio y terminación de la actividad correspondiente (Figura 6).

El segundo error conceptual está en algunos libros cuando dicen lo siguiente “El concepto y cálculo de las holguras usando el diagrama de precedencias en nada difiere del introducido para el diagrama de flechas“. En sí misma, esta frase es correcta. El error viene cuando se confunde el comienzo más tardío de la actividad con Li y el final más temprano de la actividad con Ej.
Es por todo lo anterior que, en el caso del cálculo de la holgura total, no hay ningún problema en su cálculo con el diagrama de flechas o de precedencias. Pero el resto de holguras puede ser erróneo si utilizamos un diagrama de precedencias. Veamos qué ocurre con la actividad C de este proyecto.
Holgura total: L4 – E2 – t24 = 20 – 5 – 5 = 10
Holgura libre: E4 – E2 – t24 = 10 – 5 -5 = 0
Holgura independiente: E4 – L2 – t24 = 10 – 5 – 5 = 0
Holgura condicionada: L4 – L2 – t24 = 20 – 5 – 5 = 10
Fíjese que el comienzo más tardío de la actividad C sería 15, que es un valor diferente a L2 = 5. En este caso, la terminación más temprana de la actividad C sería 10, que coincide en este caso con E4 = 10.
Conclusión: Si se usa el diagrama de precedencias, hay que tener mucho cuidado en calcular holguras de una actividad, excepto para el caso de la holgura total. En el diagrama de flechas no existe ningún problema. No confundir las fechas de comienzo más tardío y final más temprano de una actividad con los correspondientes a los nodos de entrada y salida de dicha actividad.
Referencias:
YEPES, V.; MARTÍ, J.V.; GONZÁLEZ-VIDOSA, F.; ALCALÁ, J. (2012). Técnicas de planificación y control de obras. Editorial de la Universitat Politècnica de València. Ref. 189. Valencia, 94 pp. Depósito Legal: V-423-2012.
YEPES, V. (2022). Gestión de costes y producción de maquinaria de construcción. Colección Manual de Referencia, serie Ingeniería Civil. Editorial Universitat Politècnica de València, 243 pp. Ref. 442. ISBN: 978-84-1396-046-3
YEPES, V. (2023). Maquinaria y procedimientos de construcción. Problemas resueltos. Colección Académica. Editorial Universitat Politècnica de València, 562 pp. Ref. 376. ISBN 978-84-1396-174-3

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.