números gordos – El blog de Víctor Yepes

Los motivos por los que se equivocan estudiantes y profesionales de ingeniería al abordar la resolución de problemas

Resolver problemas en el ámbito universitario o profesional, en áreas tecnológicas, de ingeniería y ciencias, puede plantear una serie de desafíos que pueden conducir a errores. Estos fallos pueden surgir por diversas razones que van desde no comprender el concepto subyacente hasta confiar demasiado en la tecnología.

En un artículo anterior mencioné algunos ejemplos de problemas teóricamente sencillos, pero que marean a nuestros estudiantes. Ahora vamos a analizar detalladamente algunas de estas razones y cómo se relacionan entre sí. También he incluido enlaces a otros artículos del blog donde reflexiono sobre este tipo de cuestiones.

La falta de comprensión del concepto subyacente a un problema es una preocupación fundamental. Esto puede manifestarse de diversas formas, ya sea a través de errores conceptuales, una aplicación incorrecta del concepto o una interpretación errónea del mismo. Esta falta de entendimiento puede empeorar si se carece de experiencia o conocimientos específicos en el campo correspondiente. Cuando un estudiante o profesional se enfrenta a un problema para el que no tiene experiencia previa, puede tener dificultades para aplicar correctamente los principios necesarios para resolverlo.

Los datos son fundamentales para encontrar soluciones, sin embargo, su calidad y disponibilidad pueden ser problemáticos. La falta de datos adecuados, la presencia de información contradictoria o sesgada pueden conducir a conclusiones incorrectas. Asimismo, centrarse excesivamente en utilizar todos los datos disponibles puede distraer de la información realmente importante, al tiempo que validar datos sesgados o inventados puede conducir a conclusiones incorrectas.

El manejo inadecuado de las bases matemáticas también puede ser una fuente de errores (geometría, trigonometría, cálculo o álgebra). Esto puede incluir errores en el cálculo, así como el uso inapropiado de fórmulas o modelos matemáticos. Los problemas reales rara vez tienen una sola solución, lo que requiere habilidades para evaluar y decidir entre múltiples enfoques posibles. Además, el uso excesivo de la memoria en lugar de la comprensión de los principios subyacentes puede conducir a errores conceptuales y de selección de modelos de cálculo.

Los aspectos psicológicos también son importantes. El estrés, la falta de confianza en uno mismo, la presión por terminar a tiempo y la falta de concentración pueden afectar a la capacidad de resolver problemas de manera efectiva. La falta de atención a los detalles, la fatiga y el agotamiento también pueden provocar errores en la resolución de problemas.

Es crucial comprender que los problemas reales pueden ser complejos y no tener necesariamente una solución única. Esto implica la necesidad de tomar decisiones informadas y comprender las limitaciones de los modelos o fórmulas utilizados. Además, la propagación de errores en las operaciones y el uso incorrecto de datos, fórmulas o software pueden dar lugar a resultados erróneos.

La falta de retroalimentación o revisión de los errores cometidos puede perpetuar la repetición de los mismos una y otra vez. La falta de comunicación o colaboración entre profesionales en entornos de trabajo también puede provocar errores en la resolución de problemas. Confiar ciegamente en la tecnología o en herramientas automatizadas sin comprender en profundidad los principios subyacentes puede ser un problema.

En resumen, resolver problemas en el ámbito universitario o profesional de la ingeniería y las ciencias puede ser un proceso complejo y propenso a errores debido a una variedad de factores interrelacionados. Desde la comprensión del concepto hasta la calidad y disponibilidad de los datos, así como los aspectos psicológicos y técnicos relacionados con la resolución de problemas, es crucial abordar estos desafíos con atención y comprensión para lograr soluciones precisas y efectivas. Desde las universidades debe hacerse todo lo posible para superar este tipo de dificultades y conseguir que nuestros estudiantes adquieran las competencias necesarias para su posterior desarrollo profesional.

Sin querer ser exhaustivo, y sin que estén ordenadas por importancia, aquí os dejo una lista de 30 posibles causas por las cuales nuestros estudiantes en los exámenes o los técnicos en su ámbito profesional, suelen cometer errores al resolver los problemas. Estoy convencido de que hay más causas, pero esto puede ser un buen punto de partida para el debate y la reflexión. En el vídeo que he grabado, me extiendo y explico algo más lo que aquí recojo como una simple lista.

La falta de comprensión del concepto subyacente en un problema puede conducir a errores conceptuales al aplicarlo incorrectamente o interpretarlo de manera errónea.
La inexperiencia o la falta de conocimientos específicos pueden surgir cuando una persona afronta por primera vez un tipo de problema, ya sea durante un examen o en la práctica profesional.
Los problemas relacionados con la disponibilidad de datos pueden presentarse de varias formas, como datos insuficientes, necesarios, innecesarios o contradictorios. A menudo, existe una obsesión por utilizar todos los datos disponibles en el enunciado del problema.
La calidad de los datos también es un factor importante, con la posibilidad de incertidumbre o error en los datos disponibles. Además, dar por válidos datos sesgados, interesados o inventados puede llevar a conclusiones incorrectas. Es necesario un control de calidad de los datos.
Intentar resolver un problema utilizando el enfoque típico visto en clase puede marear a nuestros estudiantes. Los alumnos prefieren resolver un problema típico explicado en clase, a ser posible, con datos parecidos.
El manejo inadecuado de las bases matemáticas, que incluye errores en el cálculo, el uso incorrecto de fórmulas o modelos matemáticos, y la falta de comprensión de los principios subyacentes, puede ser una fuente común de errores. La falta de conocimientos básicos de geometría, trigonometría, álgebra o cálculo básicos son, en ocasiones, escollos. A veces hay dificultades en saber dibujar un esquema para resolver el problema.
Los problemas reales generalmente no tienen una sola solución, lo que requiere habilidades para evaluar y decidir entre múltiples enfoques posibles. Esta distinción, que se da claramente entre los estudios de grado y los de máster, es importante tenerla en cuenta.
Los aspectos psicológicos, como el estrés, la falta de confianza en uno mismo, la presión por terminar a tiempo y la falta de concentración, pueden afectar negativamente la capacidad para resolver problemas de manera efectiva.
La falta de atención o interés, así como la fatiga o el agotamiento, pueden contribuir a errores en la resolución de problemas, al igual que la prisa por resolver el problema.
La complejidad de los problemas puede aumentar cuando se trata de situaciones poco comunes o rebuscadas, lo que requiere un enfoque cuidadoso y creativo para su resolución.
Es crucial comprender la diferencia entre una ley general y una fórmula particular al aplicar normas técnicas que pueden estar basadas en hipótesis o casos específicos.
Utilizar modelos de cálculo inadecuados, ya sean demasiado refinados o demasiado simples para los datos disponibles, puede conducir a soluciones incorrectas.
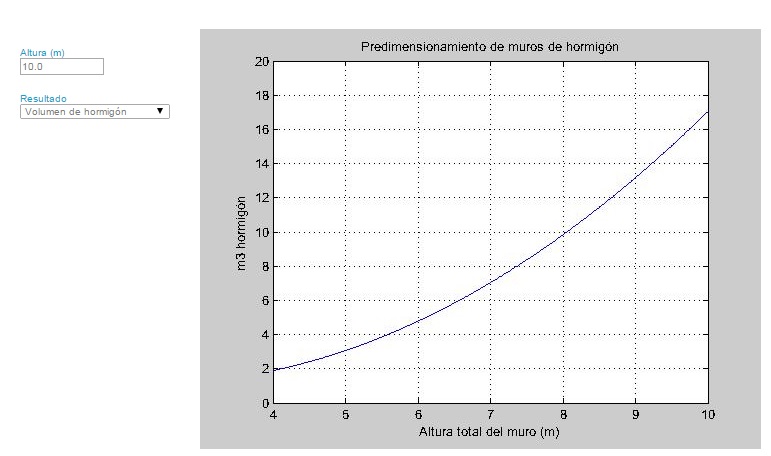
Carecer de números estimativos para prever el resultado final puede resultar en una falta de comprensión del orden de magnitud del resultado. En este sentido, el uso de nomogramas en la docencia facilita la adquisición de este tipo de habilidad en los estudiantes. Los estudiantes y los profesionales deberían tener un conocimiento del “número gordo” y saber predimensionar.
Es importante ser consciente de la propagación de errores en las operaciones, ya que incluso pequeños errores pueden magnificarse y llevar a resultados incorrectos.
Utilizar fórmulas, datos o tablas en un contexto diferente al que dieron origen puede llevar a interpretaciones incorrectas o a soluciones erróneas.
La extrapolación de resultados a límites no contemplados puede conducir a conclusiones incorrectas o poco realistas.
Utilizar fórmulas empíricas con datos expresados en unidades diferentes a las que funcionan puede generar resultados inconsistentes o incorrectos.
La dependencia excesiva de la memoria en lugar de comprender los principios subyacentes puede conducir a errores en la selección de modelos o fórmulas de cálculo.
Errores conceptuales pueden llevar a la selección incorrecta de modelos o fórmulas de cálculo, lo que resulta en soluciones erróneas.
El uso de software defectuoso o poco contrastado, así como la falta de habilidades para calcular manualmente un problema, pueden resultar en resultados incorrectos. A esto se une un uso inapropiado de la inteligencia artificial.
El mal uso de ecuaciones o fórmulas, como cambiar el nombre de una variable sin entender el concepto subyacente, puede conducir a errores en la resolución de problemas.
La falta de competencia o experiencia en una materia determinada puede resultar en una resolución incorrecta del problema.
Repetir la resolución de problemas de un contexto a otro sin pensar en su validez puede conducir a soluciones inapropiadas.
La falta de comprensión del problema, la pregunta o el tipo de resultado esperado puede resultar en soluciones incorrectas debido a la falta de comprensión lectora, capacidad analítica o de síntesis.
La utilización de unidades defectuosas, notaciones o convenciones específicas puede llevar a interpretaciones erróneas o a soluciones incorrectas.
La falta de retroalimentación o revisión de los errores cometidos puede perpetuar la repetición de los mismos errores una y otra vez.
La falta de comunicación o colaboración en entornos de trabajo entre profesionales puede contribuir a errores en la resolución de problemas.
La confianza excesiva en la tecnología o herramientas automatizadas puede llevar a la falta de comprensión de los principios subyacentes y a la comisión de errores.
La falta de revisión o verificación de los cálculos realizados por parte de un tercero independiente puede resultar en soluciones incorrectas.
La falta de conocimiento del contexto del problema, incluyendo las restricciones, puede conducir a soluciones subóptimas o incorrectas.

Os paso un vídeo donde he desarrollado las ideas anteriores, con ejemplos, y he dejado algunas de mis reflexiones al respecto. Espero que os guste.

Os dejo un podcast sobre este tema (en inglés), generado por una IA sobre el vídeo.

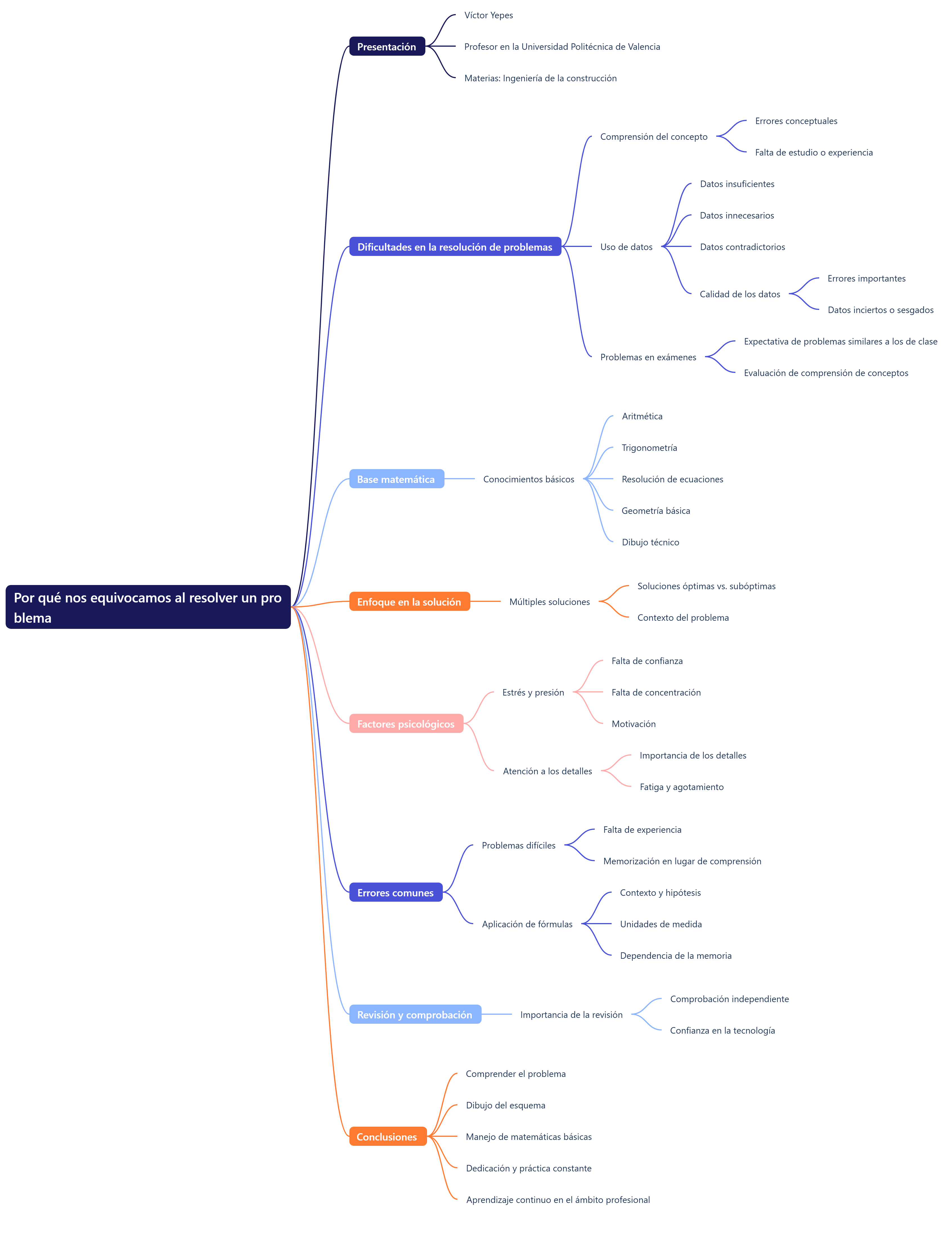
Aquí tenéis un mapa conceptual que también os puede ayudar.

Nos ha dejado Florentino Regalado, referente en la ingeniería de caminos

Figura 1. Florentino Regalado Tesoro (1950-2023), en su despacho del estudio de ingenieros. https://www.informacion.es/alicante/2023/06/13/fallece-ingeniero-caminos-florentino-regalado-88628877.html

Hoy, martes 13 de junio de 2023, al momento de escribir estas palabras, me he enterado con pesar del fallecimiento de Florentino Regalado Tesoro.

Con su partida, no solo hemos perdido a un destacado ingeniero, sino también a un ser humano excepcional y querido amigo. Aunque de manera apresurada y sin poder abarcar todo lo que quisiera, no puedo evitar dedicar unas breves líneas en su memoria. Pido disculpas por lo mucho que me dejo en el tintero, pero seguro que me sabréis perdonar.

Florentino nació en Cáceres en 1950, en el seno de una humilde familia vinculada a unas tierras de la Marquesa de Camarena, cerca de Trujillo. Tras finalizar sus estudios de ingeniero de caminos, canales y puertos en Santander, se vino a Alicante para reunirse con su hermano Ricardo.

Alguno de vosotros podéis conocerlo por haber sido el fundador de la empresa CYPE, otros por su faceta docente, por sus innumerables proyectos. Su huella se extiende por toda la provincia de Alicante, con miles de proyectos destacados en edificios de gran altura, centros comerciales, hospitales, puentes y más. Pero yo lo tengo que recordar en sus últimos años como una gran persona. Una pequeña reseña la podéis ver en el periódico Información de Alicante, un periódico donde solía escribir sobre múltiples temas, porque como me dijo un día: “quien no escribe en Información, no es nadie en Alicante”: https://www.informacion.es/alicante/2020/12/12/alicante-cabeza-26233920.html

La última vez que estuve con él personalmente fue en el VIII Congreso de la Asociación Española de Ingeniería Estructural, ACHE, que tuvo lugar en Santander el año pasado. Este congreso se tuvo que retrasar varias veces debido a la pandemia y fue un punto de reencuentro para muchos de nosotros. Aproveché para preguntarle todo aquello de lo que tenía curiosidad. Su sentido común era abrumador y su experiencia en estructuras, desbordante. A modo de ejemplo, le insinué que hoy en día, abordar el cálculo de un rascacielos supone un trabajo de modelización matemática importante que, hace apenas 30 años, era absolutamente impensable. Y la pregunta era clara: ¿cómo calculábais los rascacielos de Benidorm? Claro, quería saber cómo a finales de los 80 se podía abordar el proyecto de la estructura de un edificio como el Gran Hotel Bali de Benidorm, de 186 metros de altura y 53 plantas. Su respuesta fue de lo más inteligente: “con un par de números en una servilleta, pe ele dos partido por ocho (sic)”. Lo que me quería decir es que lo relevante es la experiencia y la comprobación conceptual con grandes números y que, luego, ya vendrían los modelos matemáticos para afinar los resultados. Ingeniería pura. Hablando en ese mismo momento sobre el desastre del terremoto de Lorca, me dio una lección en dos minutos de lo que realmente era importante en un cálculo estructural en un sismo: los detalles constructivos. También hablamos de la salud, de la familia, y de todo tipo de temas. El último día del congreso me despedí de él. Estaba alegre, se iba con su familia a su tierra natal. Luego pude ver algunas fotografías que compartió. Fue la última vez que tuve la ocasión de verle en persona.

Florentino era un apasionado del “patrimonio construido”. Hace unos años ya me contó su preocupación por dejar un montón de escritos sobre este tema que había elaborado a lo largo de su vida y que no sabía bien a quién dejar. Me dejó una fracción pequeña de sus legajos en formato digital. Afortunadamente, no se ha perdido la totalidad de sus escritos, pues me consta que el Colegio de Ingenieros de Caminos ha recibido dicho legado, que hay que ordenar, clasificar y, en su momento, hacer visible.

También fue Florentino una voz independiente y libre que, sin problema alguno, compartía con cualquier interlocutor. Las redes sociales nos han permitido, a través de un grupo de WhatsApp de los ingenieros de caminos de Alicante, conocer sus ideas, sus puntos de vista y sus debates de todo tipo. Eso sí, siempre respetuoso con las ideas de los demás. Esta misma mañana, sin conocer la fatal noticia, algún compañero le preguntaba su opinión sobre el manifiesto de la Asociación de Ingenieros de Caminos, Canales y Puertos y de la Ingeniería Civil sobre la normativa sísmica. No llegamos a tiempo.

Voy a poner un par de anécdotas personales en ese tipo de debates que, como veréis, rezumaban sentido común por todos sus poros. El último intercambio de mensajes ocurrió el 1 de junio pasado. Hacía partícipe a mis compañeros del Premio a la Excelencia Docente que había recibido del Consejo Social de la Universidad Politécnica de Valencia. Florentino me dijo: “Lástima no haberte conocido siendo estudiante”, a lo cual le contesté: “Florentino, lástima no haber coincidido contigo profesionalmente para haber aprendido lo mucho que sabes”. Son unas palabras que valen mucho más que cualquier premio, pues vienen de alguien a quien admiro mucho.

Pero no siempre coincidíamos en nuestras opiniones. Especialmente en el ámbito de las nuevas tecnologías y de la inteligencia artificial. A una noticia recogida en la prensa sobre nuestras investigaciones en optimización de estructuras con algoritmos heurísticos, Florentino me dijo lo siguiente (el lenguaje es coloquial, escrito en WhatsApp, pero sin omitir ni cambiar nada): “Víctor no acabo de explicarme cuando más sabemos, más algoritmos, más normas, más laboratorios, más de todo, mucho más costosas resultan las estructuras. LAS ECONOMÍAS SON UN MITO. Una torre en Benidorm, podía llevarse entre 25 y 30 kg de acero m2. En la actualidad ha subido como poco a los 40. Y si te descuidas puedes fabricar un Titanic. ¿Qué puñetas está pasando?”. Mi respuesta: “Florentino, un ingeniero en su vida, puede calcular 1000 estructuras. Un algoritmo inteligente revisa más de un millón en media hora. Los ahorros existen, no es un mito. El tema es que ahora las consultoras no están aprovechando las ventajas de la investigación de vanguardia. Pero en poco tiempo lo harán”. Sin embargo, no acababa de estar de acuerdo Florentino conmigo y me replicaba: “Lamento discrepar de ti, pero si para la inteligencia natural es un mito absoluto (nadie podrá darnos lo que no tiene), ya me dirás en qué consiste una construcción inteligente, frente a una construcción bien parida y bien construida. Estamos dejándonos arrastrar por un lenguaje que yo ya no entiendo su significado”. Y para zanjar el tema, y terminar de forma elegante este pequeño debate, yo le contesté: “Florentino, estoy encantado de discutir este tipo de temas en un foro como este, de técnicos. A veces se nos olvida lo que somos con otros temas. Los algoritmos no son inteligencia. Son estrategias que utilizan la fuerza bruta del ordenador para hacernos fácil el trabajo. Ingenieros como Florentino son imprescindibles para dar sentido común a lo que se investiga. La experiencia es un grado”. Ya no me pudo rebatir más, ya notábamos todos que sus fuerzas estaban mermando. ¡Maldita enfermedad!

Para acabar esta pequeña reseña personal, me he bajado a la primera planta para rebuscar entre las tesis doctorales defendidas en el Departamento de Ingeniería de la Construcción de la Universidad Politécnica de Valencia. He encontrado los dos tomos de su tesis doctoral: “Investigación y revisión crítica del conocimiento y uso de los forjados reticulares en España, con propuestas de nuevos criterios para su diseño, análisis y construcción”, dirigida por el catedrático Juan José Moragues Terrades, y defendida en el año 2001. Como podéis ver, una tesis presentada ya en la madurez profesional de Florentino. Era otra época, donde el grado de doctor solo se buscaba en el ámbito académico, y donde la publicación de artículos en revistas científicas internacionales no dejaba de ser una anécdota frente a la valía profesional. En mi caso, aunque 14 años más joven, leí la tesis también tarde, en 2002, un año después, tras casi dos décadas de experiencia profesional en empresas constructoras y en la administración pública. Pero algo ya empezaba a cambiar, tanto en nuestra universidad como en la profesión.

Para los que tengáis curiosidad, os dejo el breve resumen de su tesis doctoral, tal y como lo escribió:

“Partiendo de la realidad española del uso de los forjados reticulares, la tesis pretende sistematizar los criterios que se emplean y la razón y ser de los mismos, analizándolos arquitectónica, mecánica y constructivamente a la luz de las principales normas del mundo. Basándonos en nuestra experiencia, ensayos e investigaciones, de tipo numérico realizados sobre esta tipología de forjados, se establece, en nuestra opinión, toda una filosofía operativa que racionaliza y sistematiza el uso de los mismos, reflejando plenamente su comportamiento físico real al margen de consideraciones teóricas y escasamente representativas”.

Os dejo un par de entrevistas, también un par de conferencias donde podéis profundizar algo más en su visión personal de la ingeniería. Descansa en paz, Florentino. Te echaremos mucho de menos.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Comparativa entre el Código Estructural (CE) y la Instrucción de Hormigón Estructural (EHE-08)

Os paso a continuación un documento, en abierto, que, aunque breve, resulta muy interesante. Realiza una comparativa entre el Código Estructural y la Instrucción de Hormigón Estructural (EHE-08). Este documento se ha realizado bajo la supervisión del Instituto de Ciencias de la Construcción Eduardo Torroja (IETcc) perteneciente al Consejo Superior de Investigaciones Científicas (CSIC) y la Dirección General de Agenda Urbana y Arquitectura del Ministerio de Transportes, Movilidad y Agenda Urbana.

Además, uno de los coautores, junto con Alejandro Calle García, es mi amigo Juan Carlos Arroyo Portero, profesor de estructuras de la Universidad Politécnica de Madrid y autor, entre otros, de los libros “Números gordos en el proyecto de estructuras” y “Montoya-esencial. Hormigón armado“. Recomendables ambos dos.

El enlace a este documento lo podéis encontrar aquí: https://www.codigotecnico.org/Guias/AvanceGuiaCE.html?fbclid=IwAR1Bbq_egzA-2fDmnbA3Ocj213eizqsKA2q1CEU6jcgLGDbIs2_vcQNa5ww&fs=e&s=cl

Descargar (PDF, 4.31MB)

¿Cómo predimensionar un puente losa pretensado con aligeramientos para carreteras?

Paso superior Liria (Valencia) — Paso superior de hormigón postesado en Liria (Valencia)

Con este post continuamos una serie iniciada con el predimensionamiento de muros que puede servir para encajar presupuestos y soluciones iniciales para el caso de puentes losa pretensados empleados en carreteras (ya publicamos dos posts sobre historia y construcción de puentes viga). Para más adelante dejaremos más información sobre puentes losa pretensados macizos o bien otros empleados para ferrocarriles. Una información en detalle de estos aspectos la podéis consultar en la publicación de Yepes et al (2009).

Los tableros losa construidos “in situ” mediante cimbra se utilizan para luces cortas y medias, en torno a 30 m, pero que pueden alcanzar los 50 ó 60 m. Esta tipología, según indica Manterola (2006) representa un compromiso entre la facilidad constructiva y las condiciones resistentes. La supresión de juntas, la reducción de momentos flectores principales cuando el tablero es continuo y una mayor libertad en forma y en la colocación de las pilas son algunas de las ventajas de estas estructuras frente a las prefabricadas de vigas. Los puentes losa suelen proyectarse en tramos continuos hiperestáticos, en hormigón pretensado casi siempre. El encofrado normalmente se fabrica para cada tablero, por lo que se adaptan a cualquier trazado, prestándose a diseños más cuidados. La estética constituye, además, un aspecto importante, pues con frecuencia son las únicas obras visibles para el usuario que circula bajo ellas.

Continue reading “¿Cómo predimensionar un puente losa pretensado con aligeramientos para carreteras?” →

¿Cómo predimensionar un muro sin calculadora?

Fuerzas actuantes sobre muro de contención

Los muros de contención de tierras constituyen una de las estructuras más frecuentes en la construcción de obras civiles y de edificación, siendo habitual la tipología de muros ménsula de hormigón armado. El proyecto de estos elementos de contención constituye un problema de interacción entre el suelo y la estructura cuya finalidad consiste en retener un material de forma suficientemente segura y económica.

Los muros se proyectan basándose en la validación de un diseño inicial que se modifica sucesivamente hasta cumplir con todas las exigencias. En primer lugar, se adopta una geometría previa empleando reglas de predimensionamiento sancionadas por la práctica o referencias de casos similares. Sobre este diseño tentativo se analiza el cumplimiento de determinados requisitos de seguridad (estabilidad y resistencia) y durabilidad. Si la estructura no cumple estos requerimientos, o si lo hace de forma muy holgada, se modifica el esquema inicial y se repite el proceso.

Diseño estructural por el método de prueba y error

Todo ello conforma un panorama de procedimientos artesanales de diseño alejados de una metodología objetiva en la elección de las dimensiones y los materiales. Tales métodos conducen a proyectos seguros estructuralmente, pero cuya economía queda muy ligada a la experiencia previa del ingeniero. Con todo, una estructura no sólo debe cumplir las condiciones de seguridad, calidad y funcionalidad, sino que además debe construirse al menor coste posible.

Algunos trabajos sobre optimización han tratado de resolver el diseño automatizado de estos problemas y buscar soluciones óptimas desde el punto de vista económico y medioambiental. Para aquellos que quieran profundizar en el tema, podéis consultar las referencias.

Pero, para los que queráis predimensionar rápidamente, os paso una serie de reglas prácticas que creo son de interés y que permiten realizar presupuestos y encajes rápidos para este tipo de estructuras, siempre dentro de rangos habituales o normales (entre 4 y 10 m). Llamamos altura total la distancia entre la parte inferior de la zapata y la parte superior del alzado.

“La zapata de un muro tendrá una longitud igual a las dos terceras partes de su altura total. El canto de la zapata y el espesor del alzado serán la décima parte de la altura total. La longitud del talón será la quinta parte de la altura total más 1 metro”.

“El volumen de hormigón necesario será la sexta parte del cuadrado de la altura total, repartido en proporción 3 a 2 entre el alzado y la zapata. Además, se precisan en torno a 60 kg de acero por cada metro cúbico de hormigón”.

Para los que queráis ser más precisos, os dejo una pequeña calculadora gráfica que permite obtener dicho predimensionamiento. Basta que apretéis al botón “DIBUJAR”. Esta página se encuentra en https://laboratoriosvirtuales.upv.es/eslabon/Ejercicio?do=PredimensionamientoMuros

Referencia:

YEPES, V. (2020). Procedimientos de construcción de cimentaciones y estructuras de contención. Colección Manual de Referencia, 2ª edición. Editorial Universitat Politècnica de València, 480 pp. Ref. 328. ISBN: 978-84-9048-903-1.

YEPES, V.; ALCALÁ, J.; PEREA, C.; GONZÁLEZ-VIDOSA, F. (2008). A Parametric Study of Optimum Earth Retaining Walls by Simulated Annealing. Engineering Structures, 30(3): 821-830. ISSN: 0141-0296.

YEPES, V.; GONZÁLEZ-VIDOSA, F.; ALCALÁ, J.; VILLALBA, P. (2012). CO₂-Optimization Design of Reinforced Concrete Retaining Walls based on a VNS-Threshold Acceptance Strategy. Journal of Computing in Civil Engineering ASCE, 26 (3):378-386. DOI: 10.1061/(ASCE)CP.1943-5487.0000140.