Durante los días 23 a 25 de octubre de 2019 se celebra en la Universidad de Alicante el congreso internacional CMMoST 2019 (5th International Conference on Mechanical Models in Structural Engineering). En la sesión de mañana, a las 12:00 horas, nuestro grupo de investigación presenta en la Sala de Grados, bajo la presidencia de Salvador Ivorra, cuatro comunicaciones.
El trabajo se enmarca dentro del proyecto de investigación DIMALIFE que dirijo como investigador principal en la Universitat Politècnica de València. Os dejo aquí las referencias y los resúmenes por si os resulta de interés.
MARTÍNEZ-MUÑOZ, D.; YEPES, V.; MARTÍ, J.V. (2019). Diseño de experimentos factorial completo aplicado al proyecto de muros de contención. 5th International Conference on Mechanical Models in Structural Engineering, CMMoST 2019, 23-25 oct 2019, Alicante, Spain.
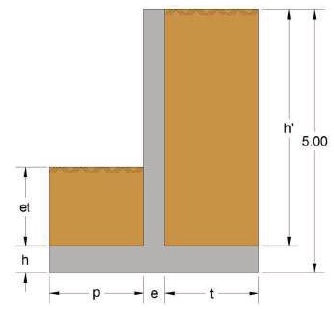
ABSTRACT: This paper applies a complete factorial design to a five-meter wall to evaluate which variables most influence the response. This method is used for two target functions, CO2 emissions and the cost of the structure. To do this, 32 evaluations of the structure are performed using a computer program and a statistical analysis is carried out. The results of this analysis show that the most statistically representative factor is the thickness of the wall and the length of the toe is of little importance for both target functions. The result of the models considering only the variables without the interaction results in an R2 greater than 95%, so the interaction between variables, although it is proven to exist, is not relevant to the case study. This methodology allows to reduce the complexity of structural problems, reducing the number of variables.
PENADÉS-PLÀ, V.; YEPES, V.; GARCÍA-SEGURA, T. (2019). Metodología para valorar la sostenibilidad con baja influencia de los decisores. 5th International Conference on Mechanical Models in Structural Engineering, CMMoST 2019, 23-25 oct 2019, Alicante, Spain.
ABSTRACT: The goal of achieving sustainable structures involves a set of criteria that are usually opposed. This leads to the need to create a decision-making process. In every decision-making process there are subjective assessments that depend on the decision-maker. This is why decision-makers become an important part of the process because of their subjective assessment. This paper proposes a methodology in which the subjective assessment of the decision-maker in the assessment of sustainability in structures is reduced. Different processes are applied to reduce uncertainty in decision-making processes. In the first place the analysis of main components is applied, in the second place the optimization based on kriging, and finally the AHP method. All this is applied to a continuous concrete deck of beams for pedestrian walkways to achieve sustainable designs, reducing the complexity in making decisions on the most sustainable solution.
YEPES, V.; PENADÉS-PLÀ, V.; GARCÍA-SEGURA, T. (2019). Aplicación de optimización Kriging para la búsqueda de estructuras óptimas robustas. 5th International Conference on Mechanical Models in Structural Engineering, CMMoST 2019, 23-25 oct 2019, Alicante, Spain.
ABSTRACT: All the structural problems have an associated variability or uncertainty. In the design of structures there are parameters such as the dimensions of the structure, the mechanical characteristics of the materials or the loads that can have variations with respect to the design value. The goal of the robust design optimization is to obtain the design that is optimum and is less sensitive to variations of these uncertain initial parameters. The main limitation of the robust design optimization is the high computational cost required due to the high number of optimizations that must be made to assess the sensitivity of the objective response of the problem. For this reason, kriging model is applied to carry out the optimization process more efficiently. In this work, it is going to apply the robust design optimization on a continuous pedestrian bridge of prestressed concrete and box section.
YEPES, V.; MARTÍNEZ-MUÑOZ, D.; MARTÍ, J.V. (2019). Optimización de muros de hormigón mediante la metodología de la superficie de respuesta. 5th International Conference on Mechanical Models in Structural Engineering, CMMoST 2019, 23-25 oct 2019, Alicante, Spain.
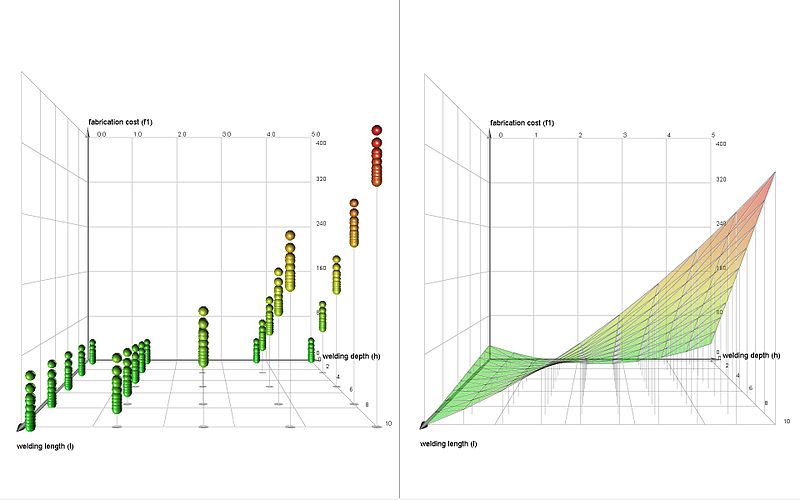
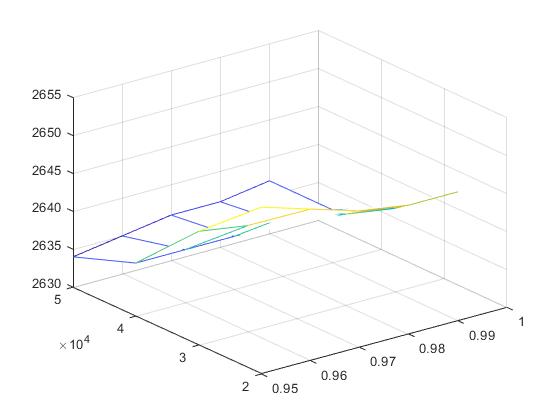
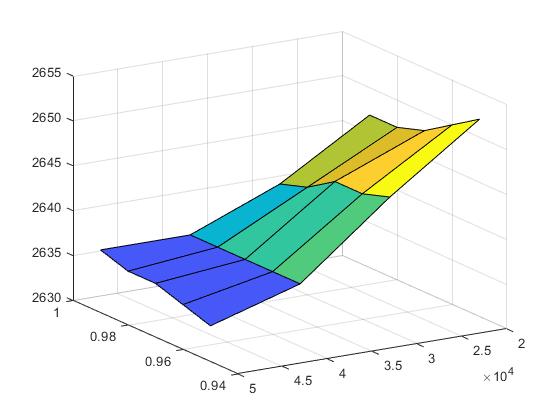
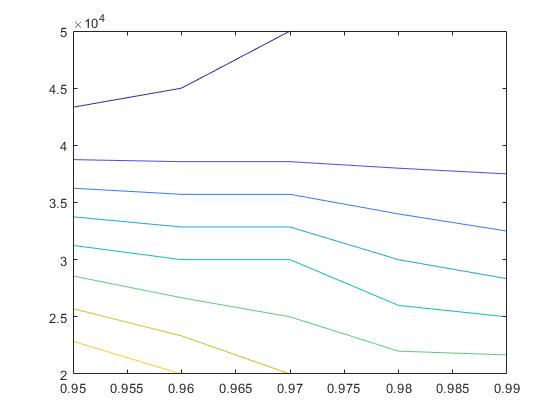
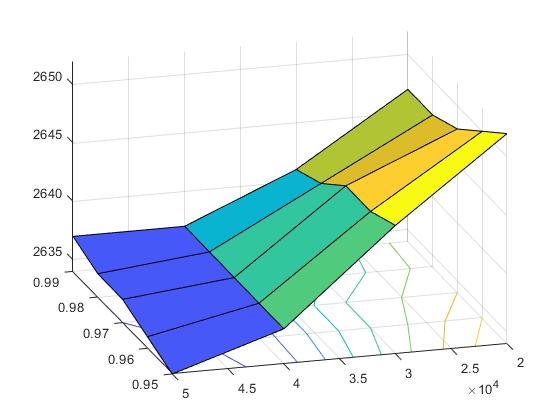
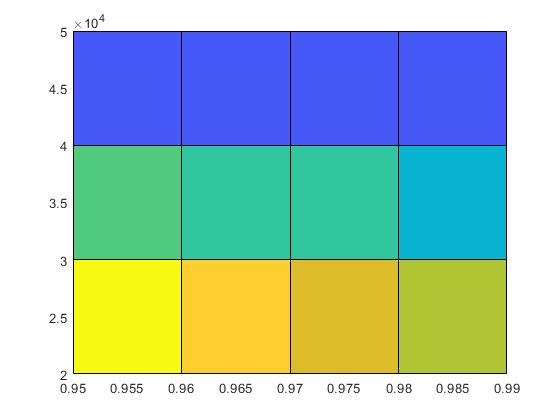
ABSTRACT: This study presents an application of the response surface methodology to optimize a 5 m high concrete wall. The objective of this research work is to obtain a design solution of a concrete wall, using the CO2 emissions as an objective function to reduce its impact. To reach this objective, a factorial experimental design has been carried out to reduce the number of variables. After this, a steepest descent method has been used to look for the optimum neighborhood. Once the region around the optimum has been found, a second order response surface has been adjusted to reach the minimum. The objective function has been modified to allow a penalty for solutions that do not meet the Ultimate Limit States or stability restrictions. With this methodology, a good solution has been obtained, while also allowing the identification of the geometric design variables that mainly affect CO2 emissions.
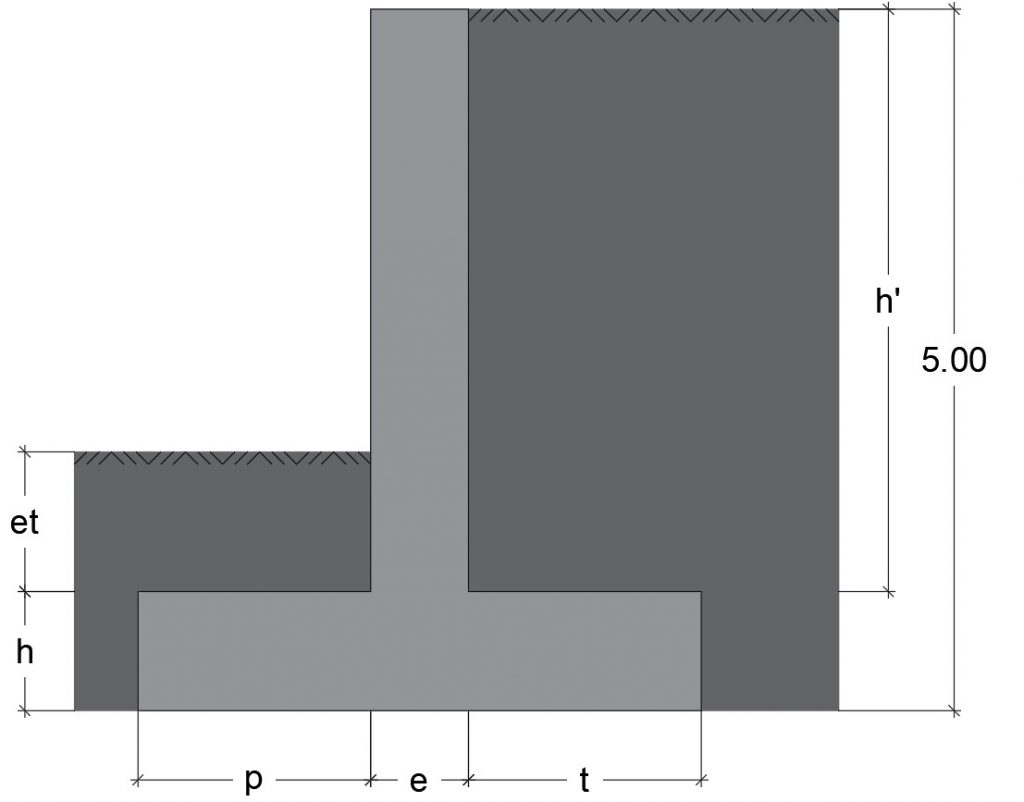Este trabajo describe la introducción de la metodología de superficie de respuesta en un curso de postgrado. Este caso se realiza en la asignatura de “Modelos predictivos y de optimización de estructuras de hormigón“. Esta asignatura se enmarca en el Plan de Estudios del Máster Universitario en Ingeniería del Hormigón. Los estudiantes aprenden aquí conceptos como la optimización de estructuras mediante algoritmos heurísticos, la toma de decisiones multicriterio, técnicas de diseño de experimentos y metamodelos como la superficie de respuesta para obtener resultados óptimos. En este caso de estudio, el objetivo es obtener una solución óptima de un muro de hormigón armado, utilizando las emisiones de CO2 como función objetivo para reducir su impacto. Para aplicar esta metodología, los estudiantes aprovechan programas comerciales. Por un lado, para realizar el análisis estadístico que permita obtener la superficie de respuesta se utiliza Minitab. Por otro lado, los estudiantes comprueban la resistencia de la estructura utilizando el software de cálculo estructural Cype. Como resultado de esta metodología se consigue que los estudiantes alcancen un mejor nivel en competencias transversales, como el diseño y el proyecto, el pensamiento crítico, el análisis y la resolución de problemas o el uso de software específico. En este trabajo se presentan futuros estudios de investigación relacionados con el uso de técnicas de optimización de estructuras por parte de los estudiantes aplicando otras técnicas de optimización diferentes.
