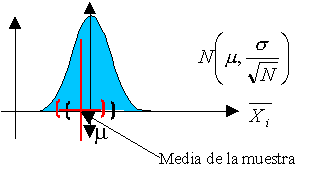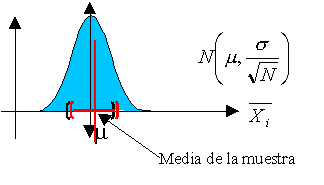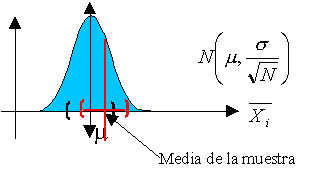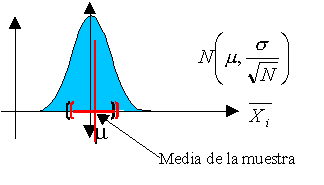
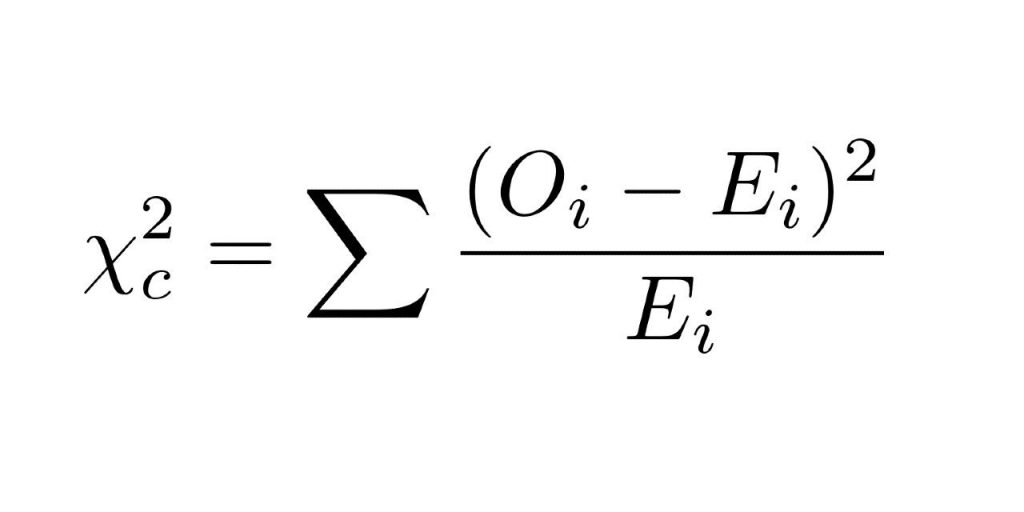Muchas veces la jerga que utilizan determinados colectivos o profesiones confunden al común de los mortales. La creación de un lenguaje jergal propio es habitual en todo grupo humano muy cerrado, con contacto estrecho y prolongado entre sus integrantes, y con una separación muy nítidamente marcada entre “dentro” y “fuera”. Un ejemplo es la jerga médica, donde la precisión necesaria para describir una enfermedad requiere de una traducción simultánea al enfermo. Otras veces existen consultores que, escudándose en neologismos, tecnicismos o anglicismos, venden mejor sus ideas o productos. No menos confuso es el lenguaje estadístico, sobre todo cuando se trata de encuestas electorales. Este lenguaje confuso, y en numerosas ocasiones deliberadamente difícil de entender, oculta ideas o conceptos sencillos. Este es el caso de las hipótesis en la investigación científica y las pruebas de hipótesis empleadas en la estadística.
Todos esperamos de un jurado que declare culpable o inocente a un acusado. Sin embargo, esto no es tan sencillo. El acusado es inocente hasta que no se demuestre lo contrario, pero el dictamen final solo puede decir que no existen pruebas suficientes para declarar que el acusado sea culpable, lo cual no es equivalente a la inocencia. Además, es fácil intuir que el jurado no es infalible. Puede equivocarse culpando a un inocente y también absolviendo a un culpable. Lo mismo ocurre con un test de embarazo o de alcoholemia, puede dar un falso positivo o un falso negativo. ¿Qué significa que una encuesta afirma que el partido “A” va a ganar las elecciones? De esto trata una prueba de hipótesis, pero vayamos por partes.
Una hipótesis puede definirse como una explicación tentativa de un fenómeno investigado que se enuncia como una proposición o afirmación. A veces las hipótesis no son verdaderas, e incluso pueden no llegar a comprobarse. Pueden ser más o menos generales o precisas, y abarcar dos o más variables, pero lo que es común a toda hipótesis, es que necesita una comprobación empírica, es decir, se debe verificar con la realidad. Pero ahora viene el problema: ¿en cuántos casos necesitamos para verificar una hipótesis? Siempre quedará la duda de que el caso siguiente negará lo planteado en la hipótesis. Por tanto, nos encontramos ante un método inductivo donde el reto será generalizar una proposición partiendo de un conjunto de datos, que denominaremos muestra.
Este tipo de hipótesis son, en realidad, hipótesis de investigación o de trabajo. Pueden ser varias, y suelen denominarse como H1, H2, …, Hi. Se trata de proposiciones tentativas que pueden clasificarse en varios tipos:
a) Descriptivas de un valor o dato pronosticado
b) Correlacionales
c) De diferencia de grupos
d) Causales.
En estadística, se llaman hipótesis nulas aquellas que niegan o refutan la relación entre variables, denominándose como H0. Estas hipótesis sirven para refutar o negar lo que afirma la hipótesis de investigación. Por ejemplo, si lo que quiero comprobar es la relación existente entre la relación agua/cemento con la resistencia a compresión a 28 días de una probeta de hormigón, entonces la hipótesis nula es que no existe una relación entre ambas variables. La idea es demostrar mediante una muestra que no existen pruebas suficientemente significativas para rechazar la hipótesis nula que indica que no existe relación entre dichas variables. Sin embargo, en un lenguaje menos formal, lo que realmente queremos es verificar que existe dicha relación. Sin embargo, también existen hipótesis alternativas, que son posibilidades diferentes de las hipótesis de investigación y nula. Así, si nuestra hipótesis de investigación establece que “esta silla es roja”, la hipótesis nula es “esta silla no es roja”, pero las hipótesis alternativas pueden ser: “esta silla es verde”, “esta silla es azul”, etc. Realmente, la hipótesis alternativas no son más que otras hipótesis de investigación. Curiosamente, en investigación no hay una regla fija para la formulación de hipótesis. Hay veces que solo se incluye la hipótesis de investigación, en otras ocasiones se incluye la hipótesis nula y, en otras, también las alternativas.
Pero, ¿se puede afirmar que un partido va a ganar las elecciones según una encuesta?, o dicho de otro modo, ¿se puede probar que una hipótesis es, con toda rotundidad, verdadera o falsa? Desgraciadamente, no se puede realizar dicha afirmación. Lo único que se puede hacer es argumentar, a la vista de unos datos empíricos obtenidos de una investigación particular, que tenemos evidencias para apoyar a favor o en contra una hipótesis. Cuantas más investigaciones, más credibilidad tendrá, y ello solo será válido para el contexto en que se comprobó. De ahí la importancia de elegir una muestra que sea suficientemente representativa de la población total. Por tanto, solo podemos argumentar la validez de las hipótesis desde el punto de vista estadístico. Las pruebas de hipótesis sirven para este cometido.
A continuación os dejo una figura donde se describe, de forma muy resumida, lo que es una prueba de hipótesis. Me gustaría que os fijaseis en que en toda prueba de hipótesis existen dos tipos de errores, el falso positivo (mandar a un inocente a la cárcel) y el falso negativo (exculpar a un culpable). Estos errores deberían ser lo más bajos posibles, pero a veces no es sencillo. Para que ambos errores bajen de forma simultánea, no hay más remedio que aumentar el tamaño de la muestra. Por este motivo, para hacer un examen lo más justo posible, este debería aprobar a los que han estudiado y suspender a los que no. Lo mejor es que el número de preguntas sea lo más alto posible.
Por tanto, ojo cuando el titular de un periódico nos ofrezca una previsión electoral. Hay que mirar bien cómo se ha hecho la encuesta y, lo más importante, saber interpretar los resultados desde el punto de vista estadístico.
Referencias:
Hernández, R.; Fernández, C.; Baptista, P. (2014). Metodología de la investigación. Sexta edición, McGraw-Hill Education, México.
El método de Monte Carlo es un procedimiento numérico que permite aproximar la resolución de expresiones matemáticas complejas con las que resulta o bien difícil, o bien imposible (especialmente en el ámbito de la estadística) encontrar resultados exactos. Con este método se puede, con la ayuda de una hoja de cálculo, llevar a cabo un ajuste del criterio de aceptación suficientemente preciso y fundado en los intereses de las partes interesadas expresados por los riesgos aceptados de común acuerdo.
