
El sistema de construcción de puentes colgantes tiene un impacto significativo en su estructura. Las fases principales en la ejecución de un puente colgante pasa por la construcción de las torres y contrapesos, el montaje de los cables principales y la ejecución del tablero.
Lo habitual es que el proceso constructivo comience con la ejecución de los anclajes y las torres. Los anclajes implican trabajos importantes de movimiento de tierras. Las torres o mástiles pueden ser de acero o de hormigón, presentando el desafío de la construcción en altura. En el caso del acero, se emplean técnicas bien desarrolladas de unión, como soldadura y tornillos de alta resistencia. Las torres de acero se montan por módulos prefabricados que se elevan mediante grúas trepadoras ancladas a la propia torre. En el caso del hormigón, se utilizan encofrados trepadores o deslizantes. En cualquier caso, se deben considerar los medios necesarios para elevar cargas de peso considerable a grandes alturas. Las grúas pueden ir creciendo a medida que las torres se elevan, estando ancladas a ellas.
Cuando los cables se anclan externamente, los contrapesos se vuelven indispensables y constituyen un elemento fundamental en la ejecución de la estructura. Los contrapesos requieren una precisa colocación de las piezas metálicas que servirán de anclaje al cable. En el caso de los puentes colgantes autoanclados, los cables principales se anclan al tablero, lo que elimina la necesidad de contrapesos. Por tanto, el tablero se convierte en el primer elemento a construir. Sin embargo, esta configuración conlleva la pérdida de una de las principales ventajas de la construcción de puentes colgantes, que es la capacidad de construir el tablero por etapas, sin importar la ubicación del puente.
Una vez ejecutadas las torres y los anclajes, es necesario proceder al montaje del cable principal, el cual constituye el elemento fundamental de la estructura resistente del puente colgante. El montaje de los cables principales es la fase más compleja, pues implica superar el vano existente entre las dos torres, lo que requiere tenderlo en el vacío. Se comienza lanzando unos cables guía, que son los primeros en abarcar la luz del puente y alcanzar los puntos de anclaje. En la mayoría de los puentes colgantes ubicados en áreas navegables, es posible pasar estos cables iniciales utilizando un remolcador. En la actualidad, este proceso ya no representa un problema gracias al uso de helicópteros e incluso drones.

A partir del cable inicial, se instalan las pasarelas que se emplean para devanar los alambres del cable, ya sea mediante alambres individuales “in situ” (air spinning) o por cordones. Durante esta etapa, el viento representa el desafío más significativo, ya que puede ocasionar grandes desplazamientos laterales en la polea móvil. En algunas ocasiones, esto ha llevado a detener el proceso de montaje del puente, generando retrasos significativos en la construcción. Finalmente, se compacta el cable principal de manera discontinua por bandas de presión o de forma continua mediante recubrimiento de alambre.
En cuanto al montaje del tablero, se suele realizar por voladizos sucesivos, avanzando simétricamente desde una torre hacia el centro del vano y hacia los extremos. También es posible llevar las dovelas a su posición definitiva mediante flotación y elevarlas desde los cables principales con cabrestantes, colgándolas en su ubicación final con las péndolas.
Una vez se han montado los cables principales, adoptando la curva catenaria correspondiente a su propio peso, se procede al montaje del tablero. El proceso de montaje del tablero se suele realizar por voladizos sucesivos, avanzando simétricamente desde una torre hacia el centro del vano y hacia los extremos. Este método requiere el uso de grúas ubicadas sobre el tablero ya construido, capaces de elevar piezas de diferentes tamaños. También es posible llevar las dovelas estancas que se transportan flotando hasta su posición y elevarlas desde los cables principales con cabrestantes, colgándolas en su ubicación final con las péndolas. Este sistema de montaje resulta más económico que el anterior y, en este caso, la secuencia de montaje se ejecuta desde el centro del vano hacia las torres, de manera simétrica.
Una vez finalizado el montaje estructural, se pasa a una fase de ajustes y comprobaciones, en la que se controlan las tensiones de los cables, la nivelación del tablero y la geometría de la catenaria. También se realizan las pruebas de carga estática y dinámica necesarias para verificar el comportamiento global antes de ponerlo en servicio.
El mantenimiento de un puente colgante comienza en el momento de su inauguración. Los cables principales, las péndolas y los anclajes están sometidos a esfuerzos continuos y a la acción de agentes ambientales agresivos, por lo que deben inspeccionarse periódicamente. Las operaciones de mantenimiento habituales incluyen la limpieza y repintado de los cables, el control de la corrosión, la sustitución de péndolas o alambres deteriorados y la supervisión del comportamiento aerodinámico frente al viento.
Una correcta planificación de estas operaciones es esencial para garantizar la durabilidad del puente y la seguridad de los usuarios a lo largo de su vida útil, que puede superar fácilmente los cien años si se mantienen adecuadamente sus componentes estructurales.
Os dejo algún vídeo sobre la construcción de este tipo de puentes. También os recomiendo mi artículo sobre la construcción del puente del Estrecho de Mackinac.
Referencias:
JURADO, C. (2016). Puentes (I). Evolución, tipología, normativa, cálculo. 2.ª edición, Madrid.
MANTEROLA, J. (2006). Puentes II. Apuntes para su diseño, cálculo y construcción. Colección Escuelas. Colegio de Ingenieros de Caminos, Canales y Puertos, Madrid.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.






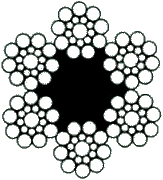
![6 x 25 [1+(6+6)+12] + (7 x 7 +0) Relleno](http://victoryepes.blogs.upv.es/wp-content/uploads/2016/03/f-150.png)
