optimización archivos - Página 15 de 18

Tesis doctoral: Diseño óptimo de estribos abiertos de hormigón armado en puentes de carretera mediante optimización heurística

Ayer 12 de enero de 2016 tuvo lugar la defensa de la tesis doctoral de D. Alejandro José Luz Ivars denominada “Diseño óptimo de estribos abiertos de hormigón armado en puentes de carretera mediante optimización heurística”, dirigida por Fernando González Vidosa y Víctor Yepes Piqueras. La tesis recibió la calificación de “Sobresaliente cum laude” por unanimidad. Presentamos a continuación un pequeño resumen de la misma.

Resumen

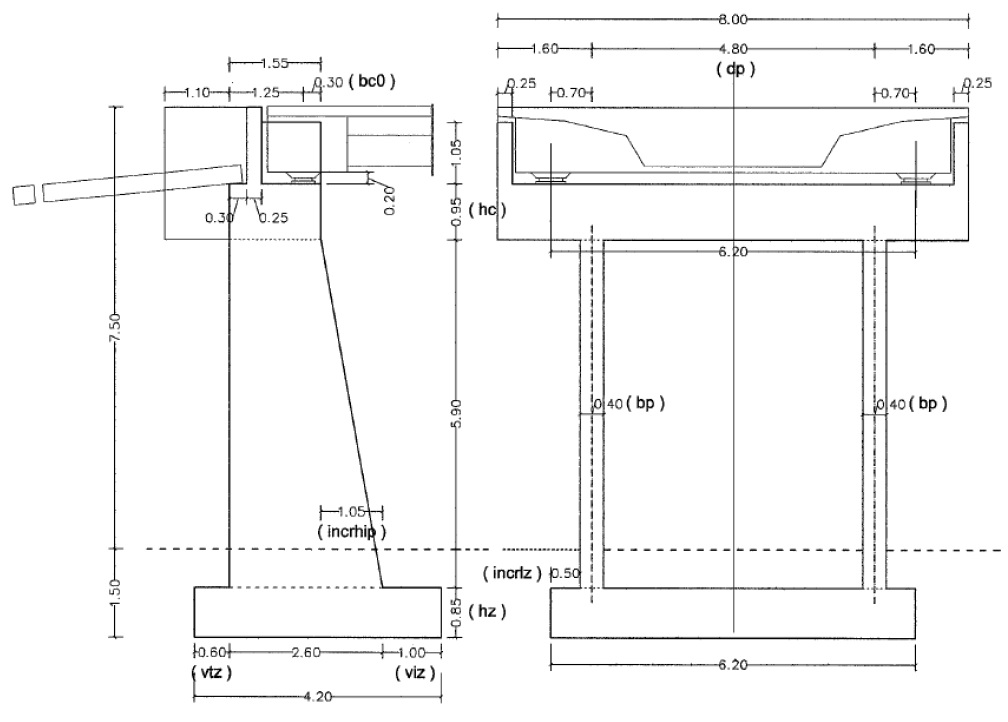
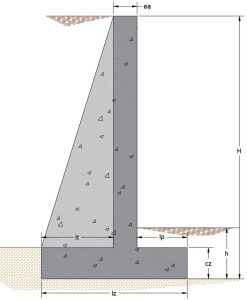
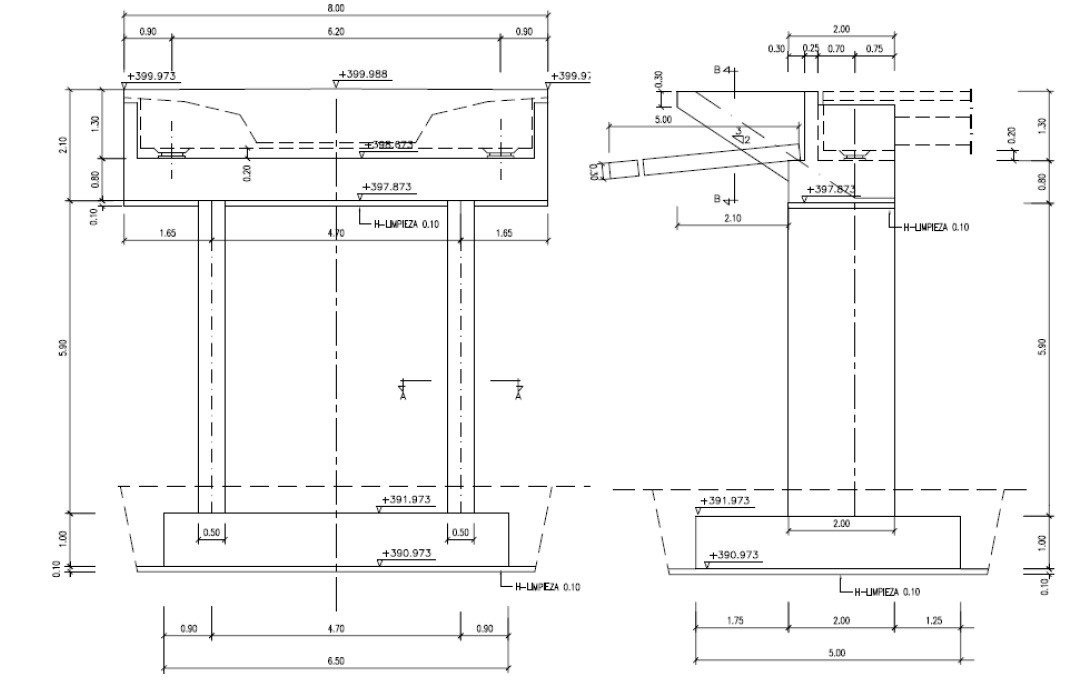
La infraestructura de mayor implantación en el territorio es la carretera. Los tramos en puente y en túnel son los más singulares y costosos, aunque los primeros son más numerosos que los segundos. Hoy en día los puentes de paso superior son uno de los más frecuentes en todas las carreteras importantes. El estribo más recomendable y habitual para este tipo de puentes es el abierto porque, se esconde bajo el terraplén, mejorando la visibilidad de los conductores de la vía inferior, y, ahorra materiales respecto al cerrado a partir de una altura de terraplén suficiente. Muchos esfuerzos se han dedicado al cálculo y diseño de los tableros de puente, menos a las pilas, y, aún menos, a los estribos. Esta tesis se ocupa del diseño óptimo de estribos abiertos de hormigón armado en puentes de carretera. Se suma a las investigaciones del Grupo de Investigación, al que pertenece de Procedimientos de la Construcción, Optimización y Análisis de Estructuras (GPRC); que ya ha optimizado tableros (de losa pretensados y de vigas artesa) y pilas (rectangulares huecas), así como, muros, bóvedas y pórticos.

Los métodos de optimización más antiguos son los exactos, pero se complican mucho y pierden eficiencia cuando el número de variables es muy alto y las condiciones que deben cumplir las soluciones (comprobaciones resistentes de los materiales) no son lineales. Por el contrario, con ayuda de los ordenadores actuales, los métodos heurísticos están en gran auge, permitiendo, con algoritmos sencillos y “mucho coste” computacional, pero en tiempo razonable, resolver de manera automática, problemas tan complejos como los reales, sin simplificaciones, y no solo optimizando el coste como hasta ahora, sino también, otros criterios o, varios a la vez, con gran facilidad. Los estribos óptimos de la tesis se obtienen mediante estos métodos heurísticos y un programa informático que se ha realizado. Están completamente diseñados para ser construidos, y para ello constan de 40 variables discretas. Los estribos no han sido antes tratados en la bibliografía de optimización. Las funciones objetivo son el coste, la seguridad estructural, la constructibilidad y la sostenibilidad ambiental, tanto de forma aislada como por parejas con el coste (con una optimización multiobjetivo híbrida MOSAMO).

Los estribos así obtenidos son diseños óptimos que no han precisado la experiencia previa de un proyectista de estructuras que proponga, como se ha venido haciendo hasta la actualidad, el diseño inicial a comprobar. Si no cumple alguna comprobación resistente (a efectuar, bien manualmente, bien, como actualmente, mediante uno o varios programas informáticos de estructuras), el diseño inicial se retoca ligeramente por el ingeniero mediante un procedimiento de prueba y error. Los programas actuales aún no incluyen rutinas de optimización como el de la tesis. Por ello la bondad del diseño final depende mucho del proyectista que los maneja y de la bibliografía que conoce. La bibliografía sobre el diseño de estribos es escasa y no completa. Este trabajo la amplía aportando las relaciones geométricas, los órdenes de magnitud y los mecanismos resistentes de los estribos óptimos (criterios de predimensionamiento) y los compara con los de la bibliografía y con los de un estribo de referencia ER. Estribo con una altura de 9 m, realmente construido y proyectado por reconocidos ingenieros, respecto al que se han comprobado ahorros económicos superiores al 18% (fundamentalmente en la zapata). Para este ER se ha realizado un estudio paramétrico obteniendo los estribos óptimos con alturas totales entre 6 y 15 m y para tensiones admisibles entre 0,2 y 0,5 MPa.

Se han empleado con éxito algoritmos heurísticos a los estribos de los dos grandes grupos existentes: por un lado, de Búsqueda Secuencial por Entornos o Hill Climbing; y, por otro, de los llamados Algoritmos Poblacionales o Evolutivos; en ambos casos, tanto con soluciones factibles como infactibles. En esta tesis, mediante una nueva propuesta de penalización de la función objetivo, se consiguen, ahorros del 60% en tiempo de cálculo. Los algoritmos empleados se basan en el recocido simulado (SAMO) y en la aceptación por umbrales (TAMO). Son dos algoritmos híbridos de escalada estocástica con operadores de mutación basados en los algoritmos genéticos. Las diferencias entre ellos no son significativas, menores del 0.2%. Con un ordenador Intel Core 2 Quad CPU Q6600 de 2.4 GHz y con 3.24 GB de memoria RAM se consigue la optimización (con penalizaciones altas) en tan solo una ejecución del algoritmo, como novedad frente a otras investigaciones, de 1 h 35’(38’ con ordenador actual). Dentro del segundo grupo se desarrollan dos nuevas heurísticas HSDLS y HSPDLS basadas en Harmony Search e hibridadas con DLS sin y con penalizaciones (y el mismo operador de mutación primer grupo) con las que se consiguen resultados similares pero con tiempos 9 y 6 veces superiores respectivamente.

Tanto la optimización monobjetivo como la multiobjetivo (MO) ponen de manifiesto la equivalencia de optimizar en coste, en CO₂ o en energía con diferencias menores del 1.5%, si bien es, a costa de un elevado número de armaduras pasivas. La optimización MO (coste barras) ofrece un ahorro medio en barras del 78.4% con un incremento medio de los otros tres criterios de 7.85% siendo el ahorro económico respecto ER todavía de un 12,23%.

Solución óptimizada — Solución optimizada

Tesis doctoral: Optimización heurística de forjados de losa postesa

Hoy 9 de diciembre de 2015 ha tenido lugar la lectura de la tesis doctoral de D. Ángel Rodríguez-Calderita Facundi denominada «Optimización heurística de forjados de losa postesa», dirigida por Víctor Yepes Piqueras y Julián Alcalá Gonzalez. La tesis recibió la calificación de «Sobresaliente cum laude» por unanimidad. Presentamos a continuación un pequeño resumen de la misma.

Resumen

El objetivo fundamental de esta tesis consiste en el desarrollo de un nuevo algoritmo de optimización que permita una mayor eficiencia que otros algoritmos empleados en la optimización de estructuras, así como la obtención de reglas de diseño a partir de los resultados de la optimización de forjados de losa postesa.

Los forjados son los elementos estructurales que se repiten constantemente en el diseño de los edificios y que, por tanto, requieren de un grado de atención importante. Por esto su optimización presenta un indudable interés. Los forjados de losa postesa, en particular, suponen una mejora tecnológica respecto a los forjados convencionales, y resultan ventajosos dentro de determinados campos de aplicación.

Del análisis de los trabajos de investigación previamente publicados, se ha podido concluir que la optimización de estructuras de hormigón en general, y de forjados losa en particular, se aborda de forma eficaz mediante el uso de metaheurísticas. El uso de estas técnicas ha demostrado ser ventajoso al hacer posible considerar todos los elementos que conforman el forjado, dando al resultado de la optimización un enfoque muy práctico pues el resultado del proceso es un forjado completamente definido.

A partir de aquí se han implementado tres algoritmos mono-objetivo basados en otras tantas metaheurísticas: el recocido simulado (SA), la aceptación por umbrales (TA) y el algoritmo del solterón, este último con dos variantes (OBA, OBA1). Estos algoritmos han sido debidamente calibrados para mejorar su funcionamiento. La comparación entre ellos muestra que funcionan de un modo muy similar. El que ha proporcionado los mejores resultados ha sido el TA, con losas entre un 0.5% y un 1% más económicas que el resto de algoritmos. El algoritmo que mejores resultados ha obtenido a continuación es casi siempre el OBA 1, pues mejora al OBA, e incluso al TA para parametrizaciones de corta duración de cálculo.

En cualquier caso, el algoritmo TA ha mejorado el coste de una solución de referencia en un 31.63%. Este ahorro tan significativo se justifica por la reducción de canto, lo que reduce la medición de hormigón, y por tanto de peso, por lo que permite reducir también cuantías de acero. Asimismo se ha implementado un algoritmo multiobjetivo (SMOSA), enfrentando dos funciones objetivo que entran en conflicto: el coste económico y la seguridad estructural, evaluada mediante un factor definido como el menor de los factores de seguridad de todos los estados límite examinados. Los resultados indican que un incremento del factor de seguridad envolvente de un 5% sobre el mínimo impuesto por las normas requiere un sobrecoste del 2%, pero esta proporción no se mantiene lineal. Para aumentar la seguridad al doble del valor normativo, el coste se incrementa en un 89.54%.

Con todos estos resultados, y analizando los resultados del algoritmo TA, se ha diseñado un nuevo algoritmo de optimización que se ha denominado Destrucción puntual más reconstrucción guiada (DP+RG). Se trata de un algoritmo inspirado en los algoritmos de destrucción-reconstrucción, con elementos de los algoritmos de búsqueda en entornos amplios. Se basa en emplear movimientos más sofisticados que dirigen la búsqueda no solo en función de la variación en la función objetivo, sino también en la alteración en el cumplimiento de los requisitos estructurales. Aunque se ha aplicado únicamente a este tipo de forjados es totalmente generalizable a la optimización de cualquier estructura de hormigón.

A pesar del requerimiento de memoria del equipo informático, este algoritmo ha resultado ser entre seis y doce veces más rápido que los algoritmos anteriores. También es más robusto, en el sentido de que las ejecuciones consecutivas del algoritmo proporcionan soluciones con una desviación máxima entre ellas del 0.29% en el peor de los casos, frente a valores de hasta el 12.5 % en el TA. Finalmente, los resultados obtenidos llegan a mejorar al TA entre un 1.1 y un 2.3% de media.

El forjado optimo desde el punto de vista económico será aquel que tenga un menor canto para la misma resistencia característica de hormigón, el canto ha resultado la variable más determinante de las analizadas lo que justifica que su ajuste se realice centímetro a centímetro y no en escalones de cinco centímetros que suele ser lo habitual.

Aplicación a la docencia de posgrado en ingeniería: la optimización de distintas tipologías de muros

Variables geométricas del muro de contrafuertes

Resumen:

Este artículo trata sobre la formación universitaria en ingeniería de proyectos en un curso de postgrado dentro del Máster en Ingeniería del Hormigón de la UPV, centrado en el diseño automatizado de estructuras de hormigón, optimizando el coste de ejecución material. El curso considera la mayoría de los algoritmos heurísticos básicos aplicándolos al diseño práctico de estructuras reales, tales como muros, pórticos y marcos de pasos inferiores de carreteras, pórticos de edificación, bóvedas, pilas, estribos y tableros de puentes. Se presentan dos tipos distintos de muros de hormigón armado in situ usados en la construcción de carreteras. Se aplica el algoritmo recocido simulado (SA), en primer lugar a un muro ménsula de 10,00 metros de altura, y en segundo lugar a un muro nervado de la misma altura. El primer modelo consta de 20 variables que definen la geometría estructural, así como las características del hormigón y los armados. El segundo modelo necesita 32 variables para su definición. Los parámetros son los mismos para los dos casos. Finalmente, se concluye que la optimización heurística es una buena herramienta para diseñar muros y comparar las distintas tipologías de proyecto, reduciendo los costes.

Palabras clave:

Educación posgrado; Diseño estructural; Optimización; Algoritmos heurísticos; Estructuras de hormigón; Muros.

Referencia:

MARTÍ, J.V.; YEPES, V. (2015). An engineering postgraduate course on heuristic design of different types of retaining walls. 19 th International Congress on Project Management and Engineering, 15-17 July, Granada (Spain).

Pincha aquí para descargar

Diseño de estribos abiertos en puentes de carretera obtenidos mediante optimización híbrida de escalada estocástica

Resumen: Este artículo se ocupa del diseño automático de estribos abiertos de hormigón armado en puentes de carretera de coste mínimo, empleando para ello dos algoritmos híbridos de escalada estocástica con operadores de mutación basados en los algoritmos genéticos. Los algoritmos empleados se basan en el recocido simulado (SAMO) y en la aceptación por umbrales (TAMO). Ambos algoritmos se aplican a un estribo definido por 40 variables discretas. Se han comprobado ahorros económicos superiores al 18 % respecto a un estribo de referencia de una altura de 9 m realmente construido, con diferencias pequeñas entre ambos algoritmos, del 0,5 % a favor de SAMO. Además, se ha realizado un estudio paramétrico para alturas de estribo entre 6 y 15 m para diferentes tensiones admisibles del terreno que ofrece criterios de predimensionamiento a los proyectistas. Se ha comprobado, además, que el ahorro económico se localiza fundamentalmente en la zapata de estas estructuras.

Palabras clave: Hormigón estructural; optimización heurística; estribos; recocido simulado; aceptación por umbrales; diseño estructural; puentes.

Cómo citar este artículo/Citation: Luz, A., Yepes, V., González-Vidosa, F., Martí, J. V. (2015). Diseño de estribos abiertos en puentes de carretera obtenidos mediante optimización híbrida de escalada estocástica. Informes de la Construcción, 67(540): e114, doi: http://dx.doi.org/10.3989/ic.14.089.

Pincha aquí para descargar

El impacto de las edificaciones en el medio ambiente

La presión demográfica mundial provoca la necesidad imperiosa de buscar alternativas sostenibles en la construcción de edificios. Efectivamente, para el año 2050 se espera que la población mundial alcance los 8900 millones de personas [1], aunque otros estudios indican que en el año 2030 esta cifra será de 9000 millones [2]. El impacto que supone esta fuerte demanda de viviendas al cambio climático es de una magnitud sin precedentes. Según datos de la UNEP (Programa de las Naciones Unidas para el Medio Ambiente) y de la OCDE (Organización para la Cooperación y el Desarrollo Económicos), el entorno edificado, representa un consumo de energía del 25 al 40%, una carga de residuos sólidos del 30 al 40% y una carga de emisión de gases de efecto invernadero del 30 al 40% [3]. En 2007, el entorno edificado consumió cerca del 47% de la energía total en China [4]. En el año 2004, los edificios agotaron, por sí solos, casi el 37% de toda la energía mundial y se espera que esta cifra alcance el 42% en el año 2030 [5]. En la India, el 24% de la energía primaria y el 30% de la energía eléctrica se consume en los edificios [6]. Casi el 10-20 % de la energía total se consume durante la construcción de los edificios, en función de las cantidades y tipos de materiales empleados, tipología de los edificios , los requisitos funcionales, la demanda de energía eléctrica y la vida útil considerada [6,7]. Algunos estudios indican que un edificio con una vida útil entre 40 y 50 años gasta durante su uso entre el 52 y el 82% de toda la energía consumida durante su ciclo de vida. A todo ello hay que añadir que una parte muy importante de los productos que se incorporan en un edificio no se ejecutan «in situ», representando un 75% de la energía necesaria para la construcción, pues son materiales con una alta demanda de energía en su fabricación [8,9].

La industria de la construcción, junto con sus industrias auxiliares, es uno de los mayores consumidores de recursos naturales, tanto renovables como no renovables, que está alterando negativamente el medio ambiente. Agota 2/5 partes de los áridos y 1/4 de la madera, y consume el 40 % de la energía total y el 16 % de agua al año [10,11]. El uso de materiales crece constantemente, con más de 23 mil millones de toneladas de hormigón producido anualmente [12,13]. En 2010, de acuerdo con la International Cement Review [14], la producción mundial de cemento se elevó a alrededor de 3,3 millones de toneladas/año , lo que significa un aumento más del 100% en casi 10 años. La producción mundial de cemento llegó a 1,6 mil millones de toneladas/año en 2001 , lo que corresponde a aproximadamente el 7 % de la cantidad mundial de dióxido de carbono liberado a la atmósfera [15,16]. Otros estudios indican que la contribución de la industria cementera a las emisiones de gases de efecto invernadero supera el 5% del total [17]. En Australia, para mantener la demanda en la construcción, se necesitan cada año aproximadamente 30 millones de toneladas de productos, más del 56 % de esta cantidad es hormigón, y el 6%, acero [18].

¿Qué podemos hacer ante este panorama? Evidentemente, es preciso un cambio de actitud a nivel mundial. La construcción y uso de los edificios va a ser creciente, como acabamos de ver. Por tanto, se hace necesaria la optimización de los recursos para que los impactos sean lo menores posibles. A modo de ejemplo, Struble y Godfrey [19] compararon el impacto ambiental producido por una viga de hormigón y otra de acero. Las de hormigón consumen menos energía y contaminan menos los recursos hídricos, sin embargo, presentan un 10% más de emisiones de CO2, aunque requieren un 60% menos de extracción de minerales [20]. Otras posibilidades pasan por la optimización en el diseño de los edificios [21-27]. Nuestro grupo de investigación ha trabajado durante estos últimos años en esta línea [28-35]. Otras líneas de trabajo tienen que ver con la certificación energética de los edificios [36]. En este sentido, La Comisión Europea, con el fin de racionalizar el uso de la energía en los edificios y aumentar su eficiencia energética, propuso la Directiva 2002/91/CE, que fue refundida en la Directiva 2010/31/UE del Parlamento Europeo y del Consejo.

Referencias:

[1] Kates, R.W. (2000). Population and consumption: what we know, what we need to know. Environment: Science and Policy for Sustainable Development, 42(3):10-19.

[2] Fernández-Solís, J. (2007). Analysis of the forces in the exponentialoid growth in construction, in: COBRA 2007, RICS Foundation.

[3] Oteiza, I.; Alonso, C. (2008). Análisis y revisión de herramientas para evaluación de la sostenibilidad de la construcción. Actas de las II Jornadas de Investigación en Construcción, pp. 1149-1166. Madrid.

[4] Wang T H (2005). China: Building a Resource-Efficient Society. China Development Forum 2005. Beijing.

[5] Urge-Vorsatz, D.; Novikova, A. (2006). Opportunities and costs of carbon dioxide mitigation in the worlds domestic sector, in: International Energy Efficiency in Domestic Appliances and Lighting Conference ‘06, London, UK.

[6] Ramesh, T.; , Prakash, R.; Shukla, K.K. (2013). Life cycle energy analysis of a multifamily residential house: a case study in Indian context, Open Journal of Energy Efficiency 2: 34–41.

[7] Bansal, D. et al. (2010). Embodied energy in residential cost effective units-up to 50 m2, in: International Conference on Sustainable Built environment(ICSBE-2010), Kandy, Sri Lanka 13–14 December.

[8] Ding, G. (2004). The development of a multi-criteria approach for the measurement of sustainable performance for built projects and facilities, Ph.D. Thesis, University of technology, Sydney, Australia.

[9] Spence, R.; Mulligan, H. (1995). Sustainable development and the construction industry, Habitat International 19 (3): 279–292.

[10] Lippiatt, B.C. (1999). Selecting cost effective green building products: BEES approach. J Constr Eng Manage 1999;125:448–55.

[11] Chong, W.K.; Kumar, S.; Haas, C.T.; Beheiry, S.M.A.; Coplen, L.; Oey, M. (2009). Understanding and interpreting baseline perceptions of sustainability in construction among civil engineers in the United States. J Manage Eng, 25(3):143–54.

[12] Schokker A.J. (2010). The sustainable concrete guide: strategies and examples. 1 ed. U.S.G.C. Council; 2010. Michigan: U.S. Green Concrete Council.

[13] World Business Council for Sustainable Development (WBCSD) (2006). Cement Industry Energy and CO2 Performance: Getting the Numbers Right; Geneva: World Business Council for Sustainable Development, (WBCSD).

[14] Intercement. Annual Report 2010: how the cement market works. <http://www.intercement.com/RS2010/pt/como-funciona-o-mercado-cimenteiro/>

[15] Mehta, P.K. (2001). Reducing the environmental: concrete can be durable and environmentally friendly. Concr Int:61–66.

[16] Bremner, T.W. (2001). Environmental aspects of concrete: problems and solutions. In: Proceedings of first all-Russian conference on concrete and reinforced concrete, Moscow, Russia.

[17] Worrell E, Price L, Martin N, Hendriks C, Meida LO (2001) Carbon dioxide emissions from the global cement industry. Annu Rev Energy Environ 26:303–329

[18] Walker-Morison, A.; Grant, T.; McAlister, S. (2007). The environmental impact of building materials. Environment design guide. PRO 7.

[19] Struble, L.; Godfrey, J. (2004). How sustainable is concrete? In: Proceedings of international workshop on sustainable development and concrete technology, Beijing, China: 2004.

[20] Miller, D.; Doh, J.H.; Mulvey, M. (2015). Concrete slab comparison and embodied energy optimisation for alternate design and construction techniques. Construction and Building Materials, 80:329-338

[21] Yeo, D.; Gabbai, R.D. (2011). Sustainable design of reinforced concrete structures through embodied energy optimization. Energy and buildings, 43(8): 2028-2033

[22] Medeiros, G.F.; Kripka, M. (2014). Optimization of reinforced concrete columns according to different environmental impact assessment parameters. Engineering Structures, 59:185-194.

[23] Bansal, D.; Singhc, R.; Sawhney, R.L. (2014). Effect of construction materials on embodied energy and cost of buildings—A case study of residential houses in India up to 60 m2 of plinth area. Energy and Buildings, 69:260-266.

[24] Asif, T. Muneer, R. Kelley, Life cycle assessment: a case study of a dwelling home in Scotland, Building and Environment 42 (2007) 1391–1394.

[25] Dixit, M.K.; Fernández-Solís, J.L.; Lavy, S.; Culp, C.H. (2010). Identification of parameters for embodied energy measurement: A literature review. Energy and Buildings, 42:1238–1247.

[26] Dixit, M.K.; Fernández-Solís, J.L.; Lavy, S.; Culp, C.H. (2012). Need for an embodied energy measurement protocol for buildings: A review paper. Renewable and Sustainable Energy Reviews, 16:3730-3743.

[27] Foraboschi, P; Mercanzin, M.; Trabucco,D. (2014). Sustainable structural design of tall buildings based on embodied energy. Energy and Buildings, 68:254-269.

[28] YEPES, V.; GARCÍA-SEGURA, T.; MORENO-JIMÉNEZ, J.M. (2015). A cognitive approach for the multi-objective optimization of RC structural problems. Archives of Civil and Mechanical Engineering, (accepted, in press).

[29] GARCÍA-SEGURA, T.; YEPES, V.; ALCALÁ, J.; PÉREZ-LÓPEZ, E. (2015). Hybrid harmony search for sustainable design of post-tensioned concrete box-girder pedestrian bridges. Engineering Structures, 92:112-122. DOI: 10.1016/j.engstruct.2015.03.015 (link)

[30] YEPES, V.; MARTÍ, J.V.; GARCÍA-SEGURA, T. (2015). Cost and CO2 emission optimization of precast-prestressed concrete U-beam road bridges by a hybrid glowworm swarm algorithm. Automation in Construction, 49:123-134. DOI: 10.1016/j.autcon.2014.10.013 (link)

[31] GARCÍA-SEGURA, T.; YEPES, V.; ALCALÁ, J. (2014). Life-cycle greenhouse gas emissions of blended cement concrete including carbonation and durability. The International Journal of Life Cycle Assessment, 19(1):3-12. DOI 10.1007/s11367-013-0614-0 (link) (descargar versión autor)

[32] MARTINEZ-MARTIN, F.J.; GONZALEZ-VIDOSA, F.; HOSPITALER, A.; YEPES, V. (2012). Multi-objective optimization design of bridge piers with hybrid heuristic algorithms. Journal of Zhejiang University-SCIENCE A (Applied Physics & Engineering, 13(6):420-432. DOI: 10.1631/jzus.A1100304. ISSN 1673-565X (Print); ISSN 1862-1775 (Online). (link)

[33] YEPES, V.; GONZÁLEZ-VIDOSA, F.; ALCALÁ, J.; VILLALBA, P. (2012). CO₂-Optimization Design of Reinforced Concrete Retaining Walls based on a VNS-Threshold Acceptance Strategy. Journal of Computing in Civil Engineering ASCE, 26 (3):378-386. DOI: 10.1061/(ASCE)CP.1943-5487.0000140. ISNN: 0887-3801. (link)

[34] PAYÁ-ZAFORTEZA, I.; YEPES, V.; HOSPITALER, A.; GONZÁLEZ-VIDOSA, F. (2009). CO₂-Optimization of Reinforced Concrete Frames by Simulated Annealing. Engineering Structures, 31(7): 1501-1508. ISSN: 0141-0296. (link)

[35] PAYÁ, I.; YEPES, V.; GONZÁLEZ-VIDOSA, F.; HOSPITALER, A. (2008). Multiobjective Optimization of Reinforced Concrete Building Frames by Simulated Annealing. Computer-Aided Civil and Infrastructure Engineering, 23(8): 596-610. ISSN: 1093-9687. (link)

[36] OWENSBY-CONTE, D.; YEPES, V. (2012). Green Buildings: Analysis of State of Knowledge. International Journal of Construction Engineering and Management, 1(3):27-32. doi: 10.5923/j.ijcem.20120103.03. (link)

Este obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Aplicación en la docencia posgrado de algoritmos heurísticos en la optimización de estructuras: Muros nervados

MARTÍ, J.V.; YEPES, V. (2015). Aplicación en la docencia posgrado de algoritmos heurísticos en la optimización de estructuras: Muros nervados. XIII Jornadas de Redes de Investigación en Docencia Universitaria, 2 y 3 de julio, Alicante, 15 pp.

Pincha aquí para descargar

Tesis doctoral sobre optimización en la gestión de activos de infraestructuras de transporte terrestre

Hoy lunes 30 de marzo de 2015 se ha defendido con éxito la tesis doctoral de la profesora Cristina Torres Machí denominada «Optimización heurística multiobjetivo para la gestión de activos de infraestructuras de transporte terrestre», que optaba a la doble titulación de doctorado, tanto de la Universitat Politècnica de València (UPV) como de la Pontificia Universidad Católica de Chile (PUC). Los directores de tesis han sido la doctora Marcela Alondra Chamorro Gine (PUC), Eugenio Pellicer Armiñana (UPV) y Víctor Yepes Piqueras (UPV). La calificación ha sido la máxima posible, de sobresaliente «cum laude» por unanimidad.

Os paso el resumen de la tesis:

«A pesar de la importancia de las infraestructuras en el desarrollo económico y social, los recursos disponibles para su conservación suelen ser insuficientes, generando un deterioro acelerado de las mismas. En este contexto surge la disciplina de gestión de activos de infraestructura, que busca optimizar la asignación de recursos para la gestión, operación y conservación de la infraestructura mediante un análisis de su ciclo de vida.

Los criterios tradicionalmente empleados para evaluar las alternativas de conservación han sido los técnicos y económicos. Si bien, recientemente, se han realizado esfuerzos para cuantificar el impacto ambiental; los modelos actuales carecen de un enfoque integrado. Surge así la oportunidad de desarrollar una evaluación sostenible que integre los aspectos técnicos, económicos y ambientales en el ciclo de vida de la infraestructura.

En relación a la asignación óptima de recursos, los métodos mayoritariamente empleados son los de programación matemática y los métodos de optimización aproximada. Dentro de estos últimos, las aplicaciones de algoritmos heurísticos resultan escasas, limitándose a resolver el problema a nivel de proyecto. Estos métodos, sin embargo, han sido exitosamente aplicados para resolver problemas de optimización combinatoria en otros campos de investigación. A esto hay que añadir que las aplicaciones desarrolladas se centran, mayoritariamente, en la optimización de un único objetivo; obviando la naturaleza multiobjetivo del problema real. Se detecta, por tanto, la oportunidad de desarrollar una herramienta de optimización heurística multiobjetivo que, considerando una evaluación sostenible de alternativas, mejore la asignación actual de recursos.

A la vista de estos antecedentes, el objetivo principal de esta investigación consiste en desarrollar una herramienta para la evaluación de alternativas de conservación y la optimización heurística multiobjetivo, que permita una asignación más sostenible y eficiente de los recursos disponibles para la conservación de redes de activos de infraestructura de transporte terrestre. La herramienta propuesta se aplica a un caso de estudio real que consiste en la gestión de una red de pavimentos urbanos en Chile.

De la aplicación de la herramienta de optimización al caso de estudio se concluye que los algoritmos heurísticos basados en búsquedas por entornos resultan poco eficientes para resolver el problema de asignación de recursos de conservación. Ante esta limitación, se desarrolla un nuevo método híbrido que considera los algoritmos GRASP (Greedy Randomized Adaptative Search Procedure), GLS (Guided Local Search) y GFB (Greedy First Best). Además, el método propuesto permite evaluar las alternativas de conservación considerando, de forma integrada, criterios técnicos, económicos y ambientales.

El algoritmo híbrido propuesto diseña programas de conservación con una efectividad media un 9% superior a la obtenida con el algoritmo de búsqueda por entornos más eficaz, requiriendo para ello un menor esfuerzo computacional. En la aplicación al caso de estudio chileno, se observa que el algoritmo híbrido mejora la gestión actual, aumentando en un 22% la condición media de la red y reduciendo, además, las emisiones de CO2 en un 12%.

En términos prácticos, los programas óptimos consideran una política proactiva, en la que los pavimentos se tratan cuando la condición de los mismos aún es buena. Por último, la herramienta propuesta mejora la planificación temporal de los recursos. En base a las evidencias demostradas en el caso de estudio, se concluye que la distribución temporal del presupuesto es un factor clave en el desempeño técnico y ambiental de la red».

Palabras Clave: Sostenibilidad; sustentabilidad; análisis del ciclo de vida; gestión de infraestructura; conservación; preservación.

Este obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Algoritmo híbrido de enjambre de luciérnagas y aceptación por umbrales para el diseño de vigas

Resumen—Este estudio convierte el diseño estructural en una optimización de variables discretas. Se propone un algoritmo híbrido de enjambre de luciérnagas para buscar soluciones con menores emisiones totales y anuales. El algoritmo combina la búsqueda colectiva de la optimización de enjambre luciérnagas “glowworm swarm optimization“(GSO) y la capacidad de búsqueda local del umbral de aceptación “threshold accepting” (TA). La estructura propuesta es una viga de hormigón en doble T biapoyada definida por 20 variables. Se estudia la resistencia del hormigón desde 30MPa hasta 100MPa. Esta comunicación propone un método para calibrar los parámetros del algoritmo con independencia de la función objetivo y del tamaño del enjambre. Los resultados muestran que TAGSO consigue diseños de vigas que emiten un 25% menos de CO2. La optimización de las emisiones anuales reduce la cantidad de CO2 al año en un 61% con un incremento total de las emisiones de CO2 del 9%.

Palabras clave-– Enjambre de luciérnagas, algoritmo híbrido, hormigón de alta resistencia, variables discretas.

Referencia: GARCÍA-SEGURA, T.; YEPES, V.; MARTÍ, J.V.; ALCALÁ, J. (2015). Algoritmo híbrido de enjambre de luciérnagas y aceptación por umbrales para diseño de vigas. X Congreso Español de Metaheurísticas, Algoritmos Evolutivos y Bioinspirados – MAEB 2015, 4-6 de febrero, Mérida, pp. 699-705. ISBN: 978-84-697-2150-6.

Pincha aquí para descargar

Optimización heurística para la gestión de infraestructuras: aplicación a una red de pavimentos urbanos en Chile

Resumen: A pesar de la importancia de las infraestructuras en el desarrollo económico y social, los recursos disponibles para su conservación suelen ser insuficientes, generando un deterioro acelerado de las mismas. En este contexto surge la disciplina de gestión de infraestructuras, la cual combina conocimientos propios de la ingeniería y economía para conseguir una asignación óptima de recursos para la gestión, operación y conservación de las infraestructuras mediante un análisis de su ciclo de vida. Sin embargo, la asignación óptima de recursos de conservación a una red de infraestructuras es un problema que no tiene una solución directa. De hecho, existen STxN soluciones factibles para una red compuesta por N activos, S posibles tratamientos de conservación y un periodo de análisis de T años. Los métodos de optimización mayoritariamente empleados para resolver este problema son los de optimización matemática y los métodos de cuasi-optimización. Sin embargo, las aplicaciones de métodos de optimización heurísticos resultan escasas y se limitan a resolver el problema de optimización a nivel de proyecto. Este trabajo presenta una herramienta de optimización heurística para el diseño de programas de mantenimiento de redes de infraestructuras. El objetivo de esta herramienta es asistir en la toma de decisiones para el mantenimiento de infraestructuras sujetas a restricciones presupuestarias. Esta herramienta se aplica a una red de pavimentos urbanos en Chile. De esta aplicación se concluye que la herramienta propuesta permite optimizar los recursos disponibles para el mantenimiento resultando en niveles de servicio superiores a los obtenidos bajo la política actual de mantenimiento.

Referencia: TORRES-MACHÍ, C.; CHAMORRO, A.; PELLICER, E.; YEPES, V.; OSORIO, A.; VIDELA, C. (2014). Optimización heurística para la gestión de infraestructuras: aplicación a una red de pavimentos urbanos en Chile. 11er Congreso Internacional PROVIAL, 20-14 octubre, Valdivia (Chile), 14 pp.

Pincha aquí para descargar

Comunicaciones presentadas al congreso MAEB 2015

A continuación vamos a presentar brevemente los resúmenes que enviamos al Congreso Nacional sobre Metaheurísticas, Algoritmos Evolutivos y Bioinspirados (MAEB). Este Congreso pretende ser un foro de encuentro, discusión y transferencia de conocimiento entre investigadores en el campo de las metaheurísticas y los algoritmos bioinspirados, con el fin de presentar e intercambiar experiencias y resultados.

La X edición, MAEB’2015, se celebrará en Mérida-Almendralejo, durante los días 4 al 6 de Febrero de 2015, y está organizada por el Centro Universitario de Mérida perteneciente a la Universidad de Extremadura. Las áreas temáticas integradas en el congreso incluyen estudios teóricos, aplicaciones prácticas, experiencias docentes y desarrollos en el campo de investigación en optimización heurística (información detallada en el apartado de llamada a la participación). Los autores agradecen el aporte financiero realizado para este trabajo por el Ministerio de Ciencia e Innovación (Proyecto de Investigación BIA2011-23602) y por la Universitat Politècnica de València (Proyecto de Investigación SP20120341).

GARCÍA-SEGURA, T.; YEPES, V.; MARTÍ, J.V.; ALCALÁ, J. (2015). Algoritmo híbrido de enjambre de luciérnagas y aceptación por umbrales para diseño de vigas. X Congreso Español de Metaheurísticas, Algoritmos Evolutivos y Bioinspirados – MAEB 2015, 4-6 de febrero, Mérida.

Este estudio convierte el diseño estructural en una optimización de variables discretas. Se propone un algoritmo híbrido de enjambre de luciérnagas para buscar soluciones con menores emisiones totales y anuales. El algoritmo combina la búsqueda colectiva de la optimización de enjambre luciérnagas “glowworm swarm optimization“(GSO) y la capacidad de búsqueda local del umbral de aceptación “threshold accepting” (TA). La estructura propuesta es una viga de hormigón en doble T biapoyada definida por 20 variables. Se estudia la resistencia del hormigón desde 30MPa hasta 100MPa. Esta comunicación propone un método para calibrar los parámetros del algoritmo con independencia de la función objetivo y del tamaño del enjambre. Los resultados muestran que TAGSO consigue diseños de vigas que emiten un 25% menos de CO₂. La optimización de las emisiones anuales reduce la cantidad de CO₂ al año en un 61% con un incremento total de las emisiones de CO₂ del 9%.

MARTÍ, J.V.; YEPES, V.; GARCÍA-SEGURA, T. (2015). Aplicación de metaheurísticas en la optimización de pasos superiores de carreteras. X Congreso Español de Metaheurísticas, Algoritmos Evolutivos y Bioinspirados – MAEB 2015, 4-6 de febrero, Mérida.

El artículo se ocupa de la optimización económica de los tableros de los pasos superiores de carreteras formados por una losa de hormigón ejecutada in situ y dos vigas artesa prefabricadas de hormigón pretensado autocompactable. Se comprueba la eficacia de las distintas metaheurísticas aplicadas en la optimización: “descent local search” (DLS), “simulated annealing” (SA), “threshold accepting” (TA), “genetic algoritms” (GA) y “memetic algorithms” (MA). Los cálculos de las tensiones y de sus envolventes, son programados en lenguaje fortran directamente por los autores. Los algoritmos de optimización heurística se aplican a un tablero de 35 m de luz y 12 m de ancho. Los parámetros que definen la forma de la sección de la viga se adaptan a los moldes de una instalación de prefabricados. El ejemplo que se analiza consta de 59 variables discretas. El módulo de la evaluación incluye los estados límite último y de servicio que se aplican comúnmente para estas estructuras: flexión, cortante, torsor, fisuración, flechas, etc. Los algoritmos SA y TA se han calibrado previamente a partir del DLS, y el MA a partir del GA y del SA. Cada heurística se procesa nueve veces, obteniéndose información estadística sobre el valor mínimo, el medio y las desviaciones. Se realiza un análisis del rendimiento de las distintas heurísticas, basado en un estudio de las soluciones Pareto-óptimas entre tiempo de ejecución y rendimiento. Los mejores resultados se obtienen para el SA y el TA, siendo el coste mínimo de 108008 €, correspondiente al SA. Finalmente, entre las principales conclusiones de este estudio, destaca que las soluciones y los tiempos de proceso computacional son tales, que estos métodos se pueden aplicar de un modo práctico a casos reales, y que el conocimiento derivado del uso de estos algoritmos permiten recomendar rangos de valores para emplearlos en el diseño optimizado de estas estructuras y en su aplicación para los predimensionados de las variables.

YEPES, V.; MARTÍ, J.V. (2015). Teoría del valor extremo como criterio de parada en la optimización heurística de puentes. X Congreso Español de Metaheurísticas, Algoritmos Evolutivos y Bioinspirados – MAEB 2015, 4-6 de febrero, Mérida.

El artículo establece un criterio de parada para un algoritmo multiarranque basado en el recocido simulado aplicado a la optimización de losas de puentes de vigas prefabricadas de hormigón pretensado. Para ello se ha comprobado que los óptimos locales encontrados constituyen valores extremos que ajustan a una función Weibull de tres parámetros, siendo el de posición, γ, una estimación del óptimo global que puede alcanzar el algoritmo. Se puede estimar un intervalo de confianza para γ ajustando una distribución Weibull a muestras de óptimos locales extraídas mediante una técnica bootstrap de los óptimos disponibles. El algoritmo multiarranque se detendrá cuando se acote el intervalo de confianza y la diferencia entre el menor coste encontrado y el teórico ajustado a dicha función Weibull.