En este artículo se explica el proyecto RESILIFE, cuyos investigadores principales son Víctor Yepes y Julián Alcalá, de la Universitat Politècnica de València. Se trata de un proyecto de investigación de carácter internacional en el que también colaboran profesores de Brasil, Chile y China. Además, se están realizando varias tesis doctorales de estudiantes de Cuba, Perú, México y Ecuador, así como de estudiantes españoles. A continuación, se describe brevemente el proyecto y se incluye una comunicación reciente donde se explica con más detalle.
En este artículo se explica el proyecto RESILIFE, cuyos investigadores principales son Víctor Yepes y Julián Alcalá, de la Universitat Politècnica de València. Se trata de un proyecto de investigación de carácter internacional en el que también colaboran profesores de Brasil, Chile y China. Además, se están realizando varias tesis doctorales de estudiantes de Cuba, Perú, México y Ecuador, así como de estudiantes españoles. A continuación, se describe brevemente el proyecto y se incluye una comunicación reciente donde se explica con más detalle.
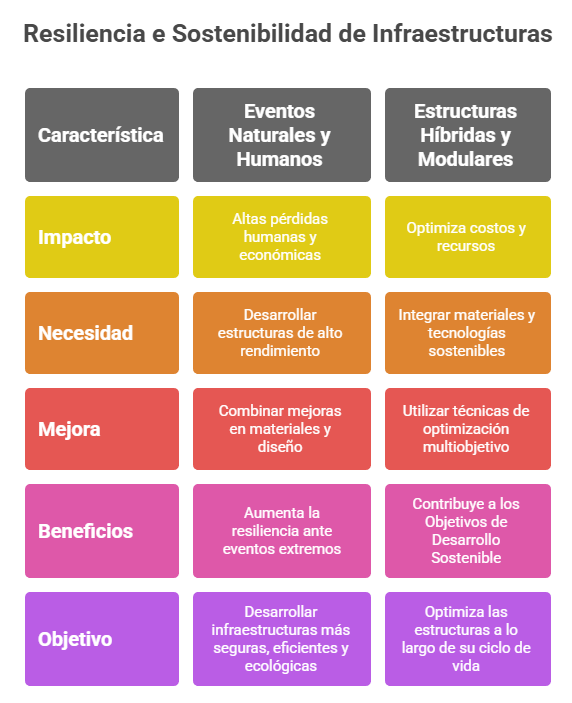
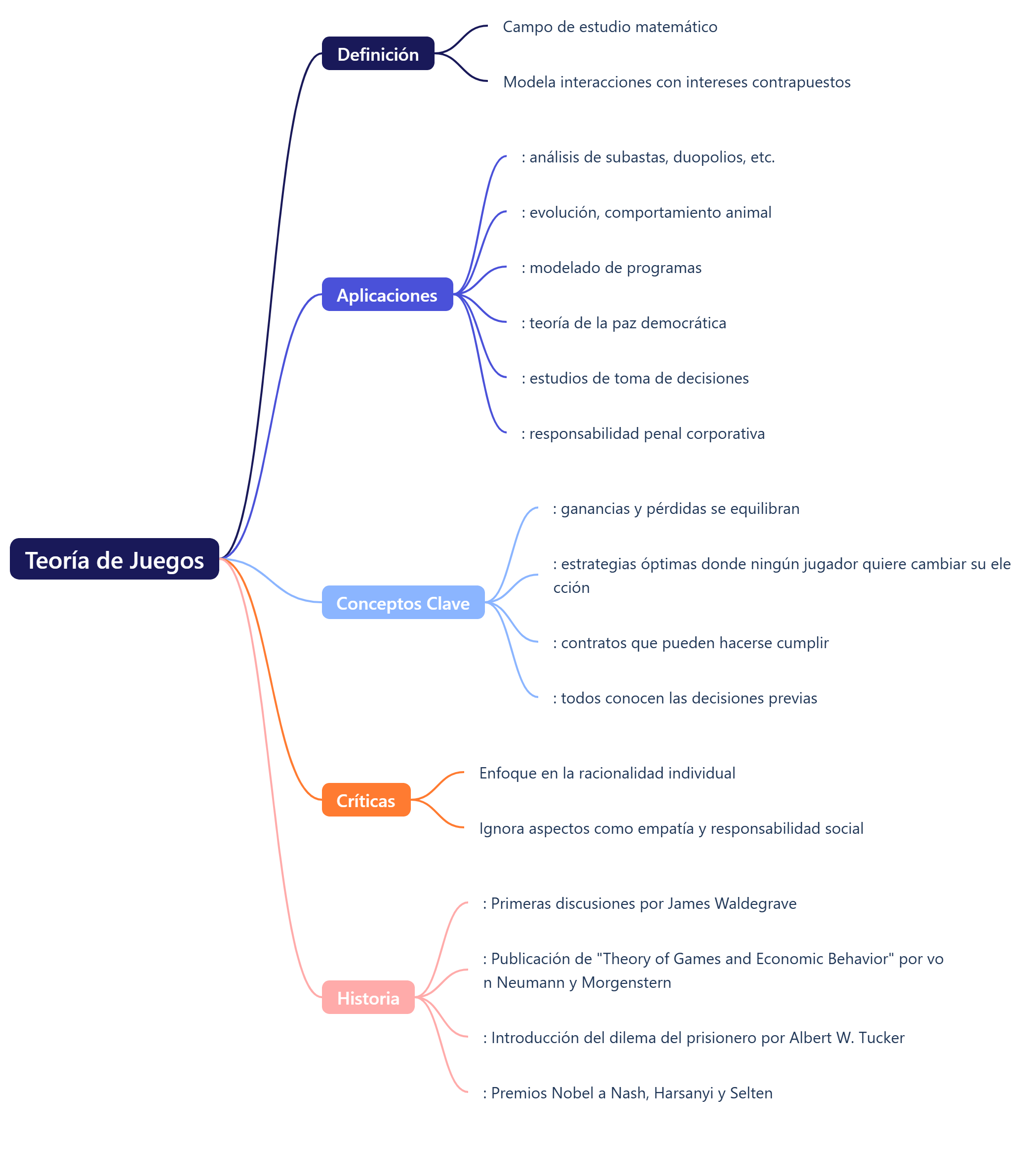
El proyecto RESILIFE se centra en optimizar de forma resiliente el ciclo de vida de estructuras híbridas y modulares para conseguir una alta eficiencia social y medioambiental, especialmente en condiciones extremas. La investigación aborda la necesidad de diseñar, construir y mantener infraestructuras que puedan resistir y recuperarse rápidamente de desastres naturales o provocados por el ser humano, minimizando las pérdidas y el impacto en la sociedad y el medioambiente. Para ello, el estudio propone utilizar inteligencia artificial, metaheurísticas híbridas, aprendizaje profundo y teoría de juegos en un enfoque multicriterio. El objetivo es mejorar la seguridad, reducir costes y optimizar la recuperación, alineándose con los Objetivos de Desarrollo Sostenible (ODS). La metodología integral incluye el análisis del ciclo de vida, así como la aplicación de lógica neutrosófica y redes bayesianas para la toma de decisiones.
¿Qué problema aborda el proyecto RESILIFE y por qué es urgente?
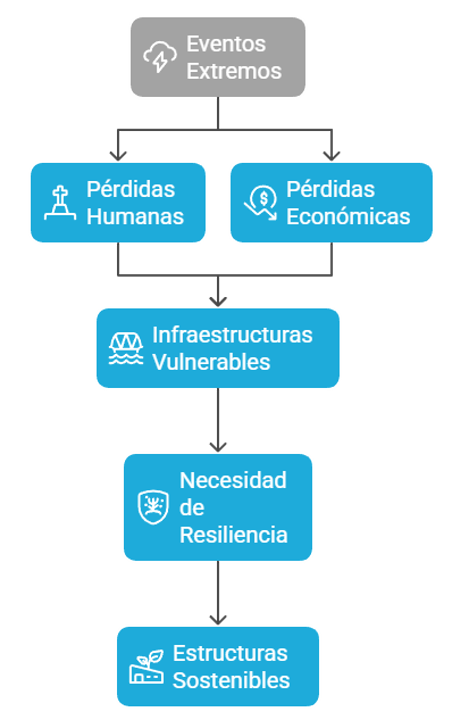
El proyecto RESILIFE aborda el desafío crítico que supone diseñar y mantener infraestructuras resilientes y sostenibles frente a desastres naturales y provocados por el ser humano. La urgencia es evidente debido a las enormes pérdidas humanas y económicas causadas por estos eventos (más de 1,1 millones de muertes y 1,5 billones de dólares en pérdidas entre 2003 y 2013), lo que subraya la necesidad de estructuras de alto rendimiento que protejan vidas y economías, al tiempo que se alinean con los Objetivos de Desarrollo Sostenible (ODS) de las Naciones Unidas. Además, los errores de diseño y construcción, así como la falta de mantenimiento, han demostrado ser causas significativas de colapso estructural, y solo el 50 % de las reparaciones de hormigón resultan efectivas en Europa.
¿Cuál es el objetivo principal de RESILIFE?
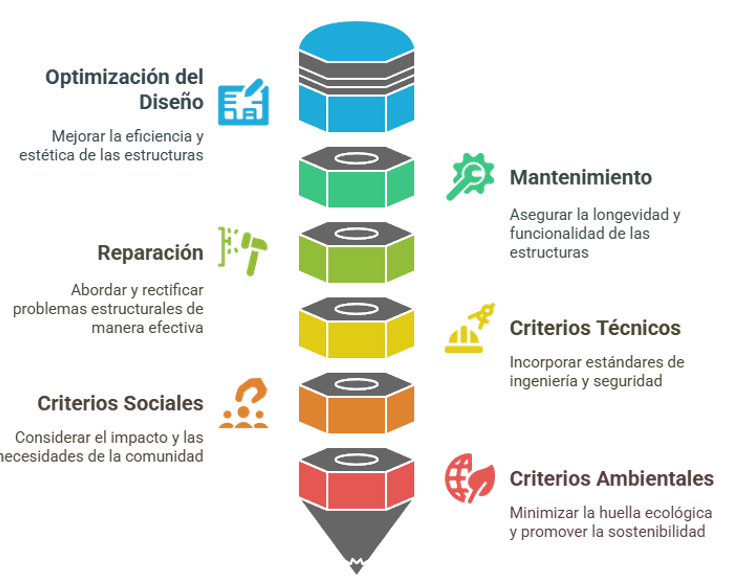
El objetivo general del proyecto RESILIFE es optimizar el diseño, el mantenimiento y la reparación de estructuras híbridas y modulares (MMC) de alta eficiencia social y medioambiental para que puedan resistir condiciones extremas. Para ello, se deben abordar problemas complejos de toma de decisiones en los ámbitos público y privado, integrando criterios de sostenibilidad social y medioambiental durante todo el ciclo de vida de las estructuras y teniendo en cuenta la variabilidad e incertidumbre inherentes al mundo real. El objetivo es que estas estructuras sean tan seguras como las tradicionales, pero con una mayor capacidad de recuperación rápida y un menor impacto social y medioambiental.
¿Qué tipos de estructuras son el foco de RESILIFE y por qué?
El proyecto se centra en estructuras híbridas (que combinan, por ejemplo, acero y hormigón) y en estructuras basadas en métodos modernos de construcción (MMC), especialmente las modulares. Estas estructuras se han elegido como objeto de estudio debido a su gran potencial para mejorar la resiliencia estructural, la eficiencia en la construcción (al reducir las interrupciones en obra y mejorar el control de calidad) y la sostenibilidad. A pesar de sus ventajas, se han identificado lagunas en la investigación sobre su optimización para eventos extremos y su aplicación en estructuras complejas, aspectos que el proyecto RESILIFE busca subsanar.
¿Qué metodologías innovadoras utiliza RESILIFE para lograr sus objetivos?
RESILIFE emplea un enfoque multidisciplinario e innovador que integra diversas técnicas avanzadas:
- Inteligencia artificial y metaheurísticas híbridas: Para optimizar el diseño, mantenimiento y reparación, mejorando la calidad de las soluciones y reduciendo tiempos de cálculo. Esto incluye el uso de deep learning.
- Teoría de juegos: Aplicada a la optimización multiobjetivo para tener en cuenta la interacción y las decisiones de múltiples actores.
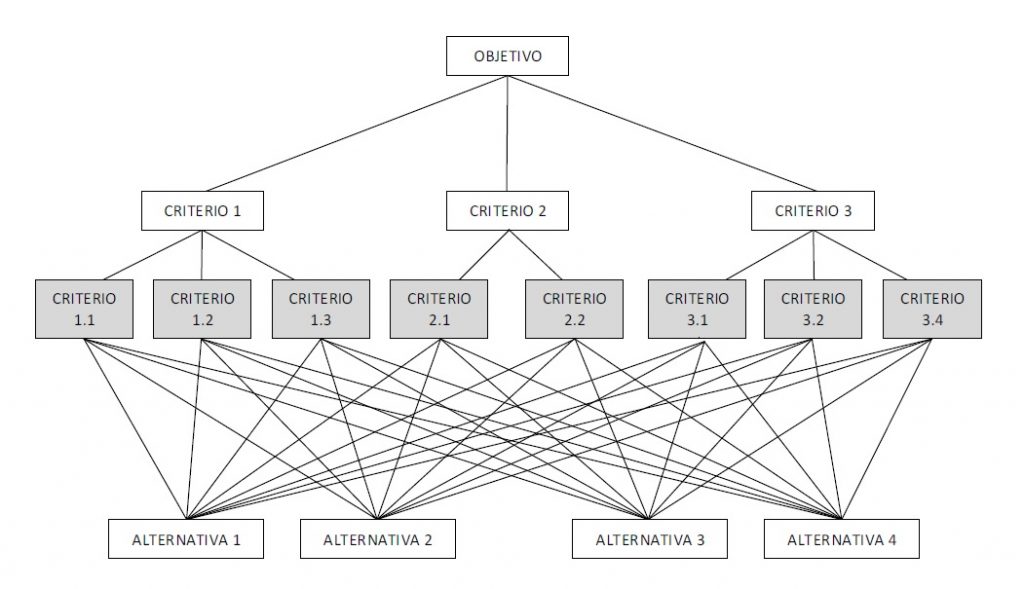
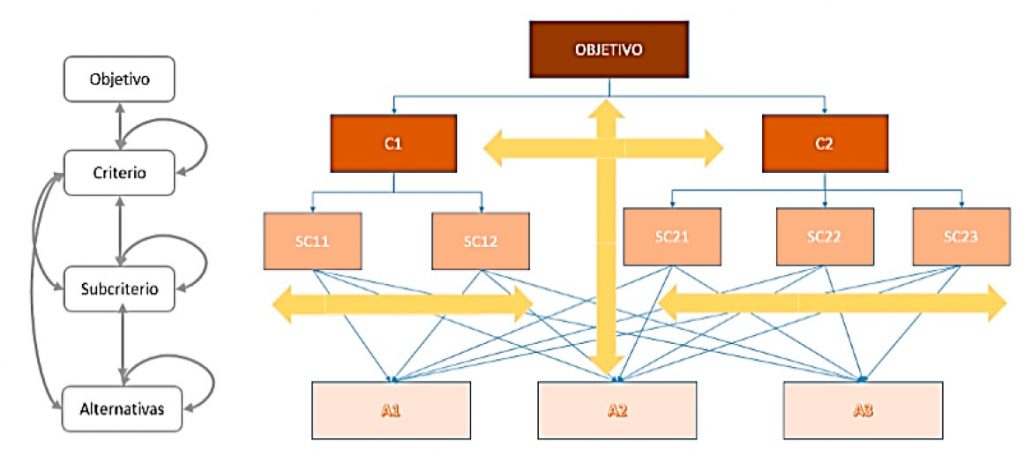
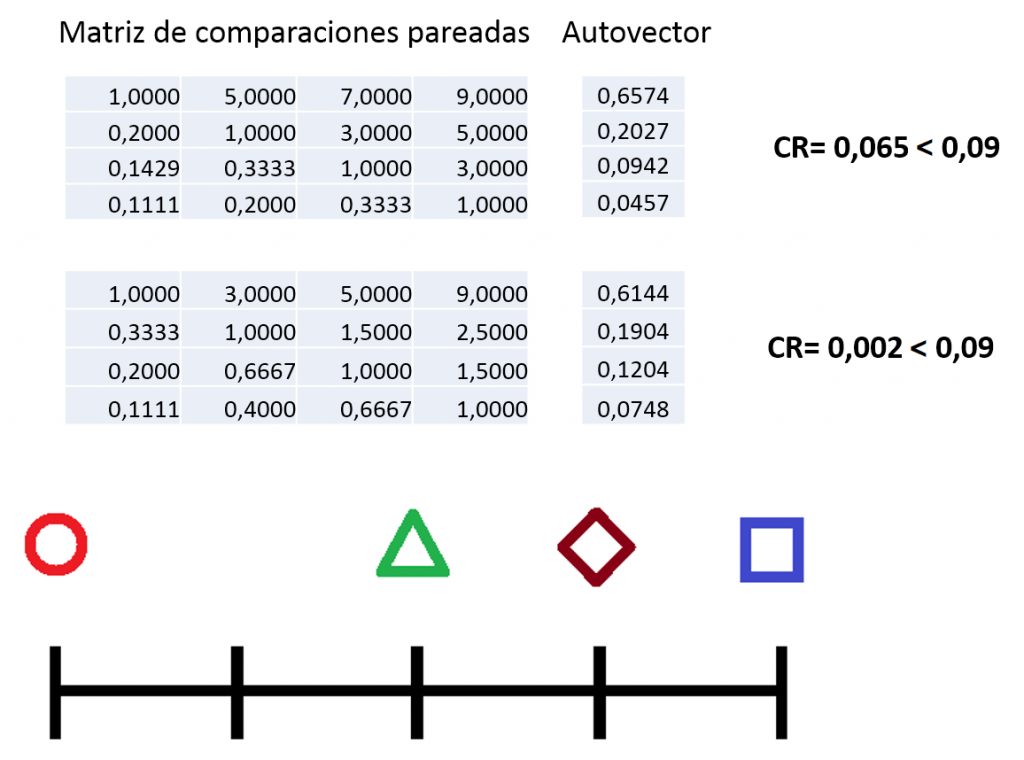
- Técnicas de decisión multicriterio: Como la lógica neutrosófica y las redes bayesianas, para manejar la incertidumbre y considerar múltiples criterios (económicos, sociales, ambientales) en la toma de decisiones.
- Análisis del ciclo de vida (ACV): Para evaluar los impactos de las estructuras desde su concepción hasta su demolición.
- Diseño óptimo robusto basado en fiabilidad: Para asegurar que las soluciones optimizadas sean viables y resistentes a pequeños cambios o incertidumbres.
- Modelado de información para la construcción (BIM) y gemelos digitales: Para integrar el proyecto estructural y ofrecer control y adaptabilidad en tiempo real.
¿Cómo aborda RESILIFE la incertidumbre y la variabilidad en el diseño y mantenimiento de estructuras?
El proyecto aborda la incertidumbre y la variabilidad mediante varias estrategias:
- Análisis de funciones de distribución de eventos extremos: Para el diseño óptimo basado en fiabilidad.
- Metamodelos y metaheurísticas híbridas basadas en fiabilidad: Permiten manejar la aleatoriedad de los parámetros y asegurar que los proyectos optimizados no sean inviables ante pequeños cambios en las condiciones.
- Técnicas de decisión multicriterio (lógica neutrosófica y redes bayesianas): Integran aspectos inciertos y criterios subjetivos en la toma de decisiones.
- Análisis de sensibilidad: De los escenarios presupuestarios y las hipótesis del ciclo de vida para identificar las mejores prácticas.
¿Qué se entiende por «resiliencia» en el contexto de RESILIFE y cómo se cuantifica?
En el contexto de RESILIFE, la resiliencia se define como la capacidad de una estructura para resistir eventos extremos, mantener su funcionalidad o recuperarla rápidamente con reparaciones mínimas tras sufrir daños, y con un bajo coste social y medioambiental. El objetivo es ir más allá de la simple resistencia y centrarse en la capacidad de adaptación y recuperación. El proyecto tiene como objetivo desarrollar procedimientos explícitos para cuantificar la resiliencia de las estructuras e infraestructuras en el contexto de múltiples amenazas, un aspecto que actualmente presenta una laguna en la investigación. Esto incluye tener en cuenta la funcionalidad técnico-socioeconómica y los impactos a lo largo de toda su vida útil.
¿Qué tipo de casos de estudio se aplican en la metodología RESILIFE?
La metodología de RESILIFE se aplica a varios casos de estudio clave:
- Optimización de pórticos de edificios altos: Con estructura de acero híbrido y hormigón armado, sometidos a un fuerte incremento de temperatura, o ante el fallo completo de soportes para evitar el colapso progresivo.
- Viviendas sociales prefabricadas en zonas sísmicas: Optimizando su resistencia a acciones extremas y su capacidad de reparación rápida.
- Mantenimiento y reparación de patologías: Resultantes de eventos extremos en diversas estructuras.
- Otras estructuras como puentes mixtos y estructuras modulares: Ampliando el alcance más allá de las viviendas. Estos casos de estudio permiten validar la aplicabilidad de las metodologías propuestas en situaciones reales y complejas.
¿Cuáles son las principales contribuciones esperadas de RESILIFE a la ingeniería estructural y la sostenibilidad?
Las principales contribuciones esperadas de RESILIFE son:
- Desarrollo de soluciones constructivas innovadoras: Como conexiones especiales y estructuras fusibles para aumentar la resiliencia y evitar el colapso progresivo.
- Formulación de metodologías de participación social: Para integrar criterios objetivos y subjetivos en decisiones multicriterio.
- Propuesta de técnicas de optimización multiobjetivo avanzadas: Basadas en metaheurísticas híbridas de deep learning, teoría de juegos y fiabilidad.
- Introducción de nuevas métricas: Que prioricen soluciones resilientes en la frontera de Pareto.
- Identificación de políticas presupuestarias efectivas: Y definición de buenas prácticas de diseño, reparación y mantenimiento robusto en construcciones MMC y estructuras híbridas.
- Avances en la modelización y evaluación: De la sostenibilidad a largo plazo y el impacto ambiental de las infraestructuras, contribuyendo a normativas y software de diseño más eficientes.
Glosario de términos clave
- Resiliencia (estructural): Capacidad de una estructura para absorber, resistir, adaptarse y recuperarse de un evento extremo, manteniendo o recuperando su funcionalidad rápidamente y con costes mínimos.
- Estructuras híbridas: Estructuras que combinan dos o más materiales estructurales diferentes, como acero y hormigón, para optimizar sus propiedades y rendimiento.
- Estructuras modulares: Estructuras compuestas por unidades o módulos prefabricados que se ensamblan en el lugar de la construcción, ofreciendo ventajas en velocidad de construcción y control de calidad.
- Eventos extremos: Desastres naturales (terremotos, tsunamis, inundaciones) o provocados por humanos (explosiones, impactos) que causan daños significativos a las estructuras y la sociedad.
- Optimización del ciclo de vida: Proceso de diseño, construcción, mantenimiento y reparación de una estructura, considerando su impacto total (económico, social, ambiental) a lo largo de toda su vida útil.
- Sostenibilidad: Principio que busca satisfacer las necesidades actuales sin comprometer la capacidad de las futuras generaciones para satisfacer sus propias necesidades, integrando aspectos ambientales, sociales y económicos.
- Inteligencia artificial (IA): Campo de la informática que dota a las máquinas de la capacidad de aprender, razonar y resolver problemas, utilizada aquí para evaluar y mejorar la resiliencia.
- Metaheurísticas híbridas: Algoritmos de optimización que combinan diferentes técnicas heurísticas o metaheurísticas para encontrar soluciones eficientes a problemas complejos, especialmente en la optimización multiobjetivo.
- Aprendizaje profundo (Deep Learning – DL): Subcampo del aprendizaje automático que utiliza redes neuronales artificiales con múltiples capas para aprender representaciones de datos, aplicado para mejorar la toma de decisiones y reducir tiempos de cálculo.
- Teoría de juegos: Rama de las matemáticas que estudia las interacciones estratégicas entre agentes racionales, aplicada en la optimización multiobjetivo para el diseño de estructuras.
- Lógica neutrosófica: Marco matemático para tratar la indeterminación y la inconsistencia, utilizado en la toma de decisiones multicriterio para manejar la incertidumbre.
- Redes bayesianas: Modelos gráficos probabilísticos que representan relaciones de dependencia condicional entre variables, empleadas en el análisis multicriterio y la gestión de incertidumbre.
- Colapso progresivo: Fenómeno en el cual un daño inicial localizado en una estructura se propaga a otras partes, llevando al colapso desproporcionado de una gran porción o de toda la estructura.
- Modern Methods of Construction (MMC): Métodos de construcción modernos que incluyen tecnologías de prefabricación, construcción modular e impresión 3D, buscando mayor eficiencia y control de calidad.
- BIM (Building Information Modeling / Modelos de Información en la Construcción): Proceso de creación y gestión de un modelo digital de un edificio o infraestructura, que facilita la integración del proyecto estructural y la toma de decisiones a lo largo del ciclo de vida.
- Metamodelo (o modelo subrogado): Modelo simplificado de un sistema complejo que permite realizar cálculos más rápidos y eficientes, crucial para reducir los tiempos de computación en la optimización.
- Diseño óptimo basado en fiabilidad: Enfoque de diseño que considera la probabilidad de fallo y las incertidumbres inherentes para optimizar las estructuras, garantizando un nivel de seguridad predefinido.
- Frontera de Pareto: Conjunto de soluciones óptimas en problemas de optimización multiobjetivo, donde ninguna de las funciones objetivo puede mejorarse sin degradar al menos otra función objetivo.
Agradecimientos:
Grant PID2023-150003OB-I00 funded by MCIN/AEI/10.13039/501100011033, and the European Regional Development Fund (ERDF), a program of the European Union (EU).