Etiqueta: regresión

En un artículo anterior hablamos del aprendizaje no supervisado aplicado a la ingeniería civil. La otra rama del aprendizaje automático (machine learning) es el aprendizaje supervisado. Se trata de un enfoque que utiliza conjuntos de datos de entrada y sus correspondientes respuestas para entrenar modelos capaces de realizar predicciones sobre datos nuevos. Este método es particularmente útil en contextos donde se dispone de información previa sobre la variable que se desea predecir, lo que permite establecer relaciones y patrones en los datos.

El aprendizaje supervisado emerge como una herramienta muy poderosa en el campo de la ingeniería civil, ya que facilita la toma de decisiones y la optimización de procesos mediante el análisis de datos. Este enfoque se basa en el uso de algoritmos que aprenden a partir de un conjunto de datos etiquetados, lo que les permite realizar predicciones sobre nuevos datos. A continuación, se presentan algunas aplicaciones y beneficios del aprendizaje supervisado en este campo.

Técnicas de aprendizaje supervisado

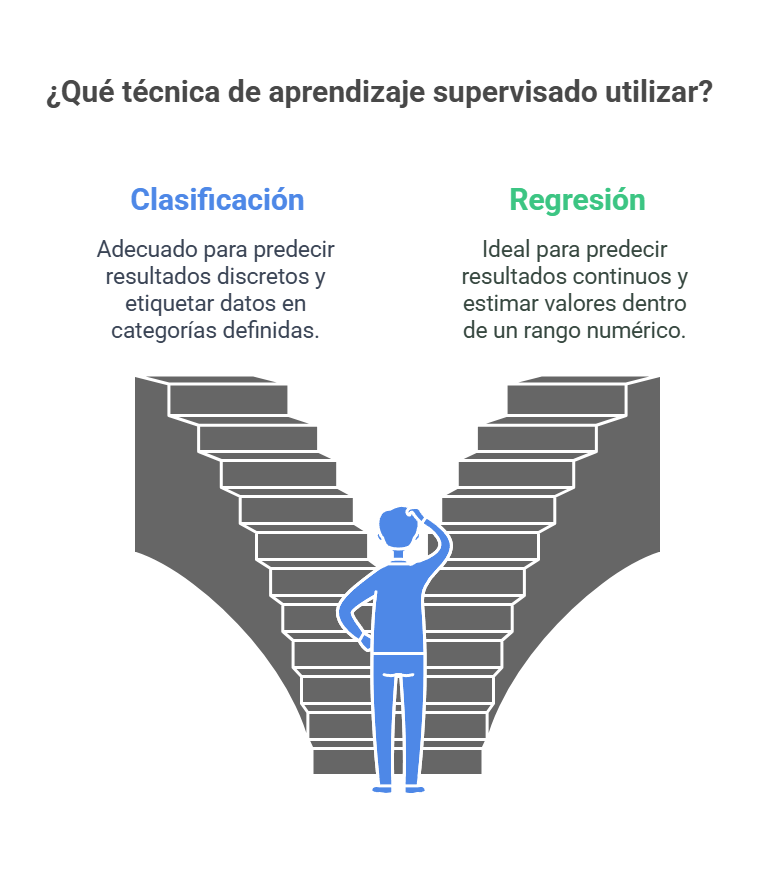
Las técnicas de aprendizaje supervisado se dividen en dos categorías principales: clasificación y regresión. La clasificación se centra en predecir respuestas discretas, es decir, en asignar una etiqueta a un conjunto de datos. Por ejemplo, en el ámbito del correo electrónico, se puede clasificar un mensaje como genuino o spam. Este tipo de modelos se aplica en diversas áreas, como la imagenología médica, donde se pueden clasificar tumores en diferentes categorías de tamaño, o en el reconocimiento de voz, donde se identifican comandos específicos. La clasificación se basa en la capacidad de los modelos para categorizar datos en grupos definidos, lo que resulta esencial en aplicaciones como la evaluación crediticia, donde se determina la solvencia de una persona.

Por el contrario, la regresión se ocupa de predecir respuestas continuas, lo que implica estimar valores en un rango numérico. Por ejemplo, se puede utilizar la regresión para prever cambios en la temperatura o fluctuaciones en la demanda eléctrica. Este enfoque es aplicable en contextos como la previsión de precios de acciones, donde se busca anticipar el comportamiento del mercado, o en el reconocimiento de escritura a mano, donde se traduce la entrada manual en texto digital. La elección entre clasificación y regresión depende de la naturaleza de los datos y de la pregunta específica que se desea responder.

Selección del algoritmo adecuado.

La selección de un algoritmo de aprendizaje automático es un proceso que requiere un enfoque metódico, ya que hay que encontrar el equilibrio entre diversas características de los algoritmos. Entre estas características se encuentran la velocidad de entrenamiento, el uso de memoria, la precisión predictiva en nuevos datos y la transparencia o interpretabilidad del modelo. La velocidad de entrenamiento se refiere al tiempo que un algoritmo necesita para aprender de los datos, mientras que el uso de memoria se relaciona con la cantidad de recursos computacionales que requiere. La precisión predictiva es crucial, ya que determina la capacidad del modelo para generalizar a datos no vistos. Por último, la interpretabilidad se refiere a la facilidad con la que se pueden entender las decisiones del modelo, lo que es especialmente relevante en aplicaciones donde la confianza en el modelo es esencial.

El uso de conjuntos de datos de entrenamiento más grandes generalmente permite que los modelos generalicen mejor en datos nuevos, lo que se traduce en una mayor precisión en las predicciones. Sin embargo, la selección del algoritmo también puede depender del contexto específico y de las características de los datos disponibles.

Clasificación binaria y multicategoría

Al abordar un problema de clasificación, es fundamental determinar si se trata de un problema binario o multicategórico. En un problema de clasificación binaria, cada instancia se clasifica en una de las dos clases, como ocurre cuando se identifica la autenticidad de los correos electrónicos o su clasificación como spam. Este tipo de clasificación es más sencillo y, por lo general, se puede resolver con algoritmos diseñados específicamente para este propósito. En contraste, un problema de clasificación multicategórica implica más de dos clases, como clasificar imágenes de animales en perros, gatos u otros. Los problemas multicategóricos suelen ser más complejos, ya que requieren modelos más sofisticados que puedan manejar la diversidad de clases y sus interacciones.

Es importante señalar que algunos algoritmos, como la regresión logística, están diseñados específicamente para problemas de clasificación binaria y tienden a ser más eficientes durante el entrenamiento. Sin embargo, existen técnicas que permiten adaptar algoritmos de clasificación binaria para abordar problemas multicategóricos, lo que amplía su aplicabilidad.

Algoritmos de clasificación comunes

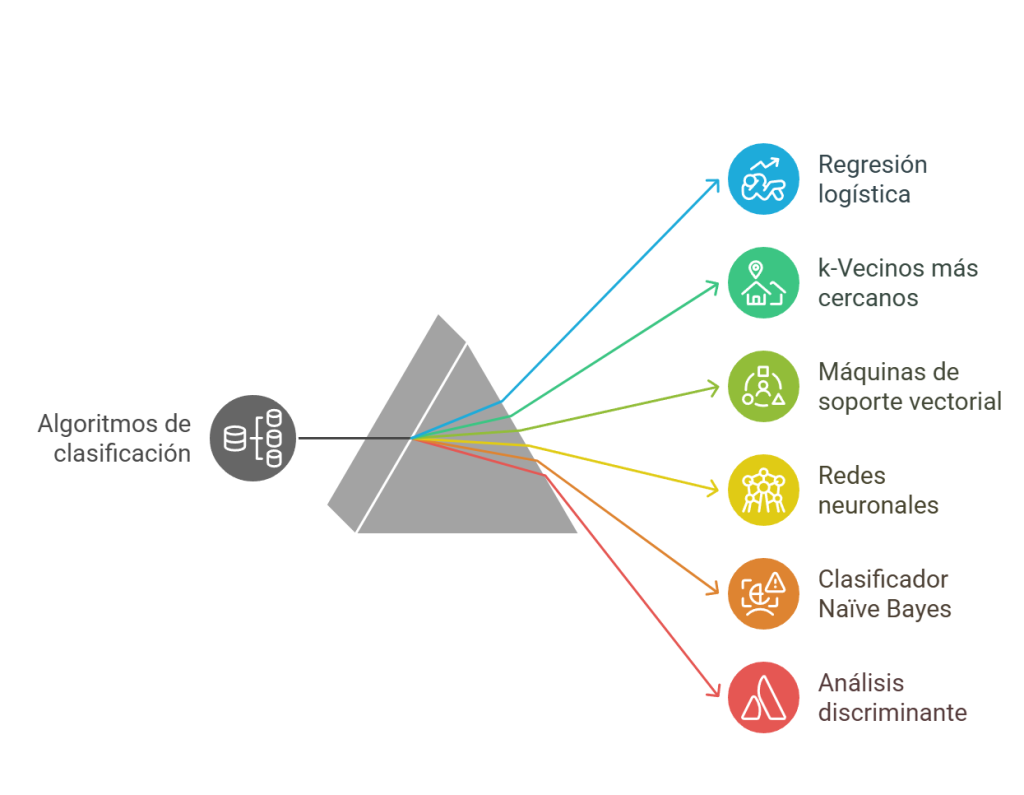
Existen diversos varios algoritmos de clasificación ampliamente utilizados en el campo del aprendizaje supervisado.

• La regresión logística es uno de los métodos más comunes, ya que permite predecir la probabilidad de que una respuesta binaria pertenezca a una de las dos clases. Este algoritmo es valorado por su simplicidad y se emplea frecuentemente como punto de partida en problemas de clasificación binaria. Su capacidad para ofrecer una interpretación clara de los resultados lo convierte en una herramienta muy valiosa en diversas aplicaciones.
• El algoritmo k-vecinos más cercanos (kNN) clasifica objetos basándose en las clases de sus vecinos más cercanos, utilizando métricas de distancia como la euclidiana o la de Manhattan. Este enfoque es intuitivo y fácil de implementar, aunque puede resultar costoso en términos de cálculo en conjuntos de datos grandes.
• El soporte vectorial (SVM) es otro algoritmo destacado que clasifica datos al encontrar un límite de decisión lineal que separe las clases. En situaciones en las que los datos no son linealmente separables, se puede aplicar una transformación de kernel para facilitar la clasificación. Este método es especialmente útil en contextos de alta dimensionalidad, donde la complejidad de los datos puede dificultar la clasificación.
• Las redes neuronales, inspiradas en la estructura del cerebro humano, son útiles para modelar sistemas altamente no lineales. Estas redes se entrenan ajustando las conexiones entre neuronas, lo que permite que el modelo aprenda patrones complejos en los datos. Aunque su interpretación puede ser más complicada, su capacidad para capturar relaciones no lineales las hace valiosas en diversas aplicaciones.
• El clasificador Naïve Bayes se basa en la suposición de que la presencia de una característica en una clase no depende de la presencia de otras características. Este enfoque permite clasificar nuevos datos en función de la probabilidad máxima de pertenencia a una clase, lo que resulta útil en contextos en los que se requiere una clasificación rápida y eficiente.
• El análisis discriminante clasifica los datos mediante combinaciones lineales de características, asumiendo que los diferentes conjuntos de datos tienen distribuciones gaussianas. Este método es apreciado por su simplicidad y facilidad de interpretación.
• Los árboles de decisión permiten predecir respuestas basándose en decisiones tomadas en un árbol estructurado, donde cada rama representa una condición de decisión. Este enfoque es intuitivo y fácil de interpretar, por lo que es una opción popular en diversas aplicaciones.

Algoritmos de regresión comunes

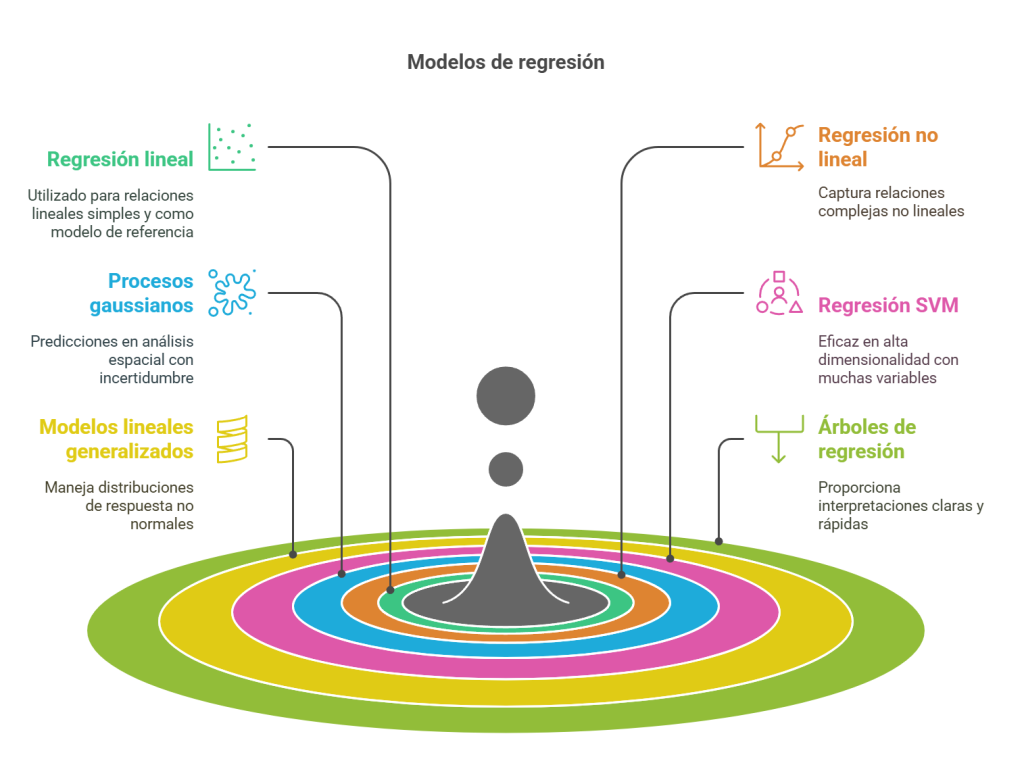
Los algoritmos de regresión son esenciales para predecir valores continuos.

• La regresión lineal es una técnica que describe una variable de respuesta continua como una función lineal de una o más variables predictoras. Este modelo es fácil de interpretar y se utiliza frecuentemente como referencia para modelos más complejos. Su simplicidad y eficacia en contextos lineales lo convierten en una opción inicial para el análisis de datos.
• La regresión no lineal se utiliza cuando los datos presentan tendencias no lineales significativas. Este enfoque permite modelar relaciones más complejas que no pueden ser capturadas por modelos lineales, lo que resulta útil en contextos donde las variables interactúan de manera no lineal.
• El modelo de regresión de procesos gaussianos es un enfoque no paramétrico que se utiliza para predecir valores continuos y es común en el análisis espacial. Este método es especialmente valioso en contextos donde se requiere interpolación y se trabaja con datos que presentan incertidumbre.
• La regresión SVM, similar a su contraparte de clasificación, busca un modelo que se desvíe de los datos medidos en la menor cantidad posible. Este enfoque es útil en contextos de alta dimensionalidad, donde se espera que haya un gran número de variables predictoras.
• El modelo lineal generalizado se utiliza cuando las variables de respuesta tienen distribuciones no normales, lo que permite abordar una variedad de situaciones en las que no se cumplen los supuestos de la regresión lineal.
• Los árboles de regresión son una adaptación de los árboles de decisión que permiten predecir respuestas continuas, por lo que son útiles en contextos donde se requiere una interpretación clara y rápida.

Mejora de modelos

La mejora de un modelo implica aumentar su precisión y capacidad predictiva, así como prevenir el sobreajuste, que ocurre cuando un modelo se ajusta demasiado a los datos de entrenamiento y pierde capacidad de generalización. Este proceso incluye la ingeniería de características, que abarca la selección y transformación de variables, y la optimización de hiperparámetros, que busca identificar el conjunto de parámetros que mejor se ajustan al modelo.

• La selección de características es un aspecto crítico en el aprendizaje supervisado, especialmente en conjuntos de datos de alta dimensión. Este proceso permite identificar las variables más relevantes para la predicción, lo que no solo mejora la precisión del modelo, sino que también reduce el tiempo de entrenamiento y la complejidad del mismo. Entre las técnicas de selección de características se encuentran la regresión por pasos, que implica agregar o eliminar características de manera secuencial, y la regularización, que utiliza estimadores de reducción para eliminar características redundantes.
• La transformación de características es otra estrategia importante que busca mejorar la representación de los datos. Técnicas como el análisis de componentes principales (PCA) permiten realizar transformaciones lineales en los datos, que capturan la mayor parte de la varianza en un número reducido de componentes. Esto resulta útil en contextos donde se trabaja con datos de alta dimensionalidad, ya que facilita la visualización y el análisis.
• La optimización de hiperparámetros es un proceso iterativo que busca encontrar los valores óptimos para los parámetros del modelo. Este proceso puede llevarse a cabo mediante métodos como la optimización bayesiana, la búsqueda en cuadrícula y la optimización basada en gradientes. Un modelo bien ajustado puede superar a un modelo complejo que no ha sido optimizado adecuadamente, lo que subraya la importancia de este proceso en el desarrollo de modelos efectivos.

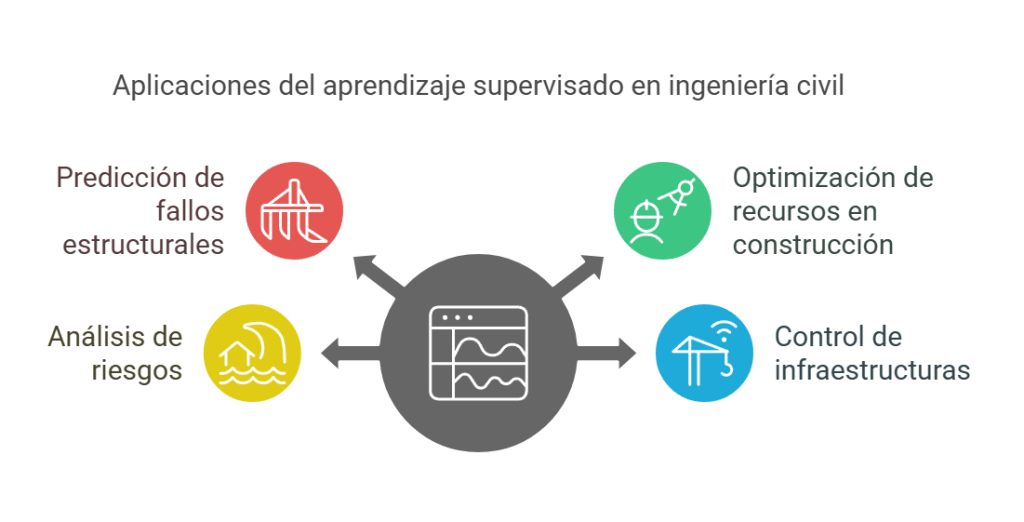
Aplicaciones del aprendizaje supervisado en ingeniería civil

• Predicción de fallos estructurales: los modelos de aprendizaje supervisado se utilizan para predecir fallos en estructuras como puentes y edificios. Al analizar datos históricos de inspecciones y condiciones ambientales, es posible identificar patrones que indiquen un posible fallo estructural. Esto permite a los ingenieros realizar mantenimientos preventivos y mejorar la seguridad de las infraestructuras.
• Optimización de recursos en construcción: en la planificación de proyectos, el aprendizaje supervisado optimiza el uso de recursos como, por ejemplo, materiales y mano de obra. Al predecir la demanda de recursos en función de variables como el clima y la evolución del proyecto, es posible reducir costes y mejorar la eficiencia.
• Análisis de riesgos: los modelos de aprendizaje supervisado son útiles para evaluar riesgos en proyectos de ingeniería civil. Al analizar datos sobre desastres naturales, como inundaciones y terremotos, se pueden identificar zonas vulnerables y desarrollar estrategias de mitigación eficaces.
• Control de infraestructuras: la incorporación de sensores en infraestructuras permite la recolección de datos en tiempo real. Los algoritmos de aprendizaje supervisado pueden analizar estos datos para detectar anomalías y prever el mantenimiento necesario, lo que contribuye a la sostenibilidad y durabilidad de las estructuras.

Por tanto, el aprendizaje supervisado se está consolidando como una herramienta esencial en ingeniería civil, ya que ofrece soluciones innovadoras para predecir, optimizar y controlar infraestructuras. Su capacidad para analizar grandes volúmenes de datos y ofrecer información valiosa está transformando la forma en que se gestionan los proyectos en este ámbito.

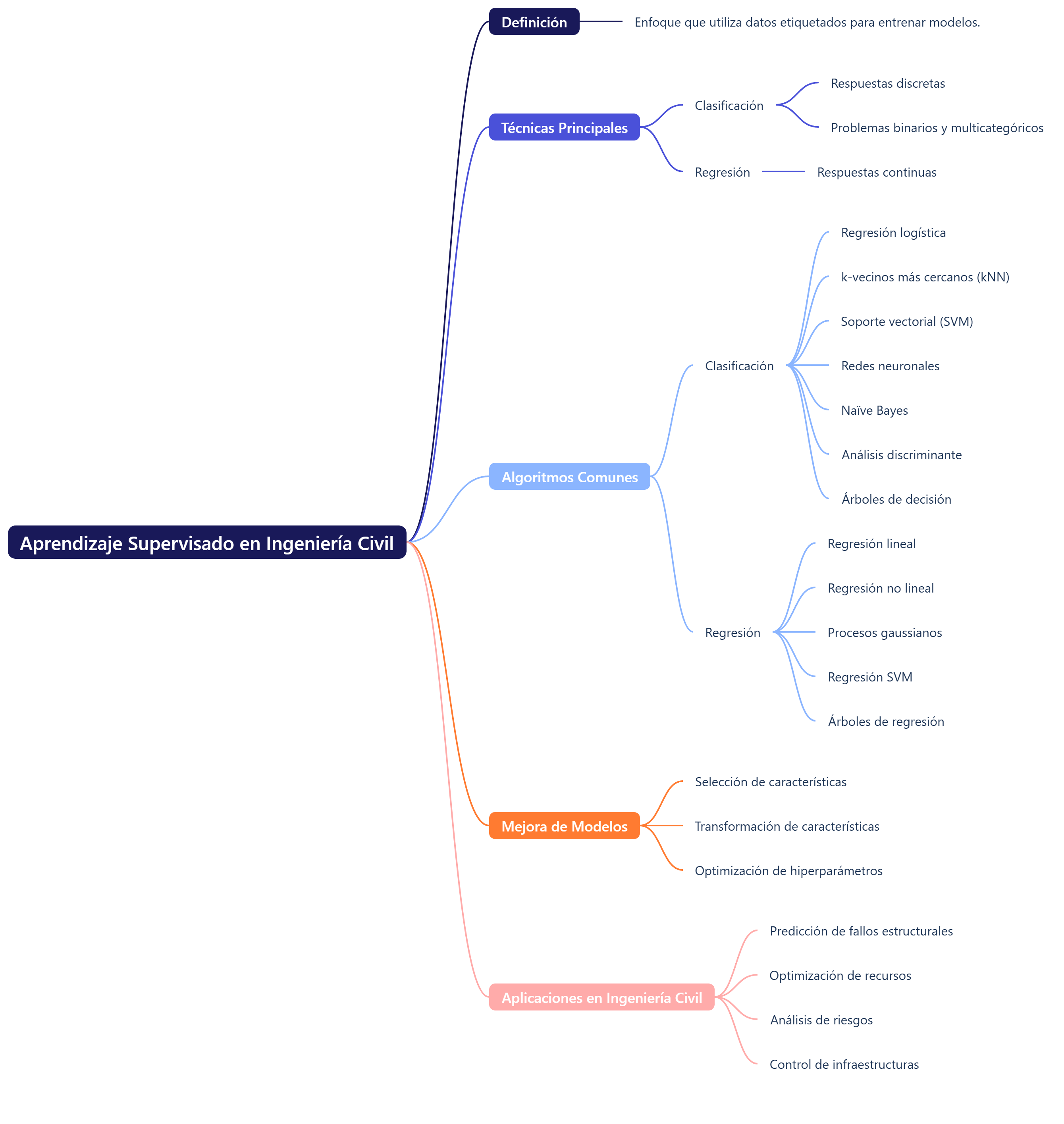
Os dejo un mapa mental acerca del aprendizaje supervisado.

También os dejo unos vídeos al respecto. Espero que os sean de interés.

Referencias

1. Garcia, J., Villavicencio, G., Altimiras, F., Crawford, B., Soto, R., Minatogawa, V., Franco, M., Martínez-Muñoz, D., & Yepes, V. (2022). Machine learning techniques applied to construction: A hybrid bibliometric analysis of advances and future directions. Automation in Construction, 142, 104532.
2. Kaveh, A. (2024). Applications of artificial neural networks and machine learning in civil engineering. Studies in computational intelligence, 1168, 472.
3. Khallaf, R., & Khallaf, M. (2021). Classification and analysis of deep learning applications in construction: A systematic literature review. Automation in construction, 129, 103760.
4. Mostofi, F., & Toğan, V. (2023). A data-driven recommendation system for construction safety risk assessment. Journal of Construction Engineering and Management, 149(12), 04023139.
5. Naderpour, H., Mirrashid, M., & Parsa, P. (2021). Failure mode prediction of reinforced concrete columns using machine learning methods. Engineering Structures, 248, 113263.
6. Reich, Y. (1997). Machine learning techniques for civil engineering problems. Computer‐Aided Civil and Infrastructure Engineering, 12(4), 295-310.
7. Thai, H. T. (2022). Machine learning for structural engineering: A state-of-the-art review. In Structures (Vol. 38, pp. 448-491). Elsevier.

Descargar (PDF, 1.52MB)

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.