1. ¿Qué es un acuífero y cómo se clasifica?
Un acuífero es una formación geológica subterránea que contiene y transmite agua. Se clasifican principalmente en:
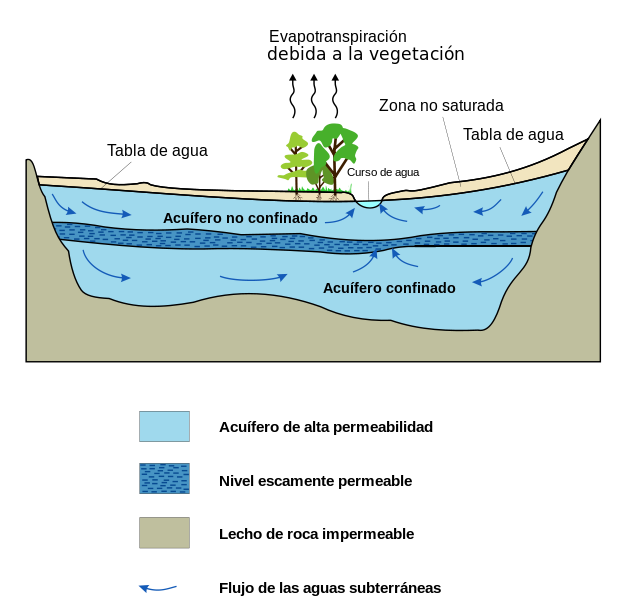
- Acuífero libre: El agua está en contacto con la atmósfera a través de los poros o las fisuras de la zona no saturada. El límite superior es el nivel freático, donde la presión del agua es atmosférica.
- Acuífero confinado: El acuífero está cubierto por una capa impermeable (acuicludo o acuitardo) y el agua se encuentra a una presión superior a la atmosférica. Si se perfora un pozo en un acuífero confinado y el agua sube por encima de la superficie del terreno, se dice que existen existen «condiciones artesianas».
Además, existen otras formaciones relevantes:
- Acuicludo: Una formación geológica que, aunque contiene agua, no la transmite de manera efectiva, por lo que no es apta para su explotación (por ejemplo, terrenos arcillosos).
- Acuitardo: Transmite el agua muy lentamente, por lo que no es apto para su captación, pero puede permitir la recarga vertical de otros acuíferos en condiciones especiales (por ejemplo, arcillas limosas o arenosas).
2. ¿Qué es la carga hidráulica total y por qué es importante la Ley de Darcy en el estudio del flujo de agua en medios porosos?
La carga hidráulica total (H), también conocida como potencial, representa la energía por unidad de peso de un fluido en movimiento, expresada como una altura. Incluye la altura geométrica (z), la altura de presión (u/γw) y la altura de velocidad (v²/2g). En el contexto del flujo en medios porosos, la velocidad suele ser despreciable, por lo que la carga total se simplifica a la altura piezométrica.
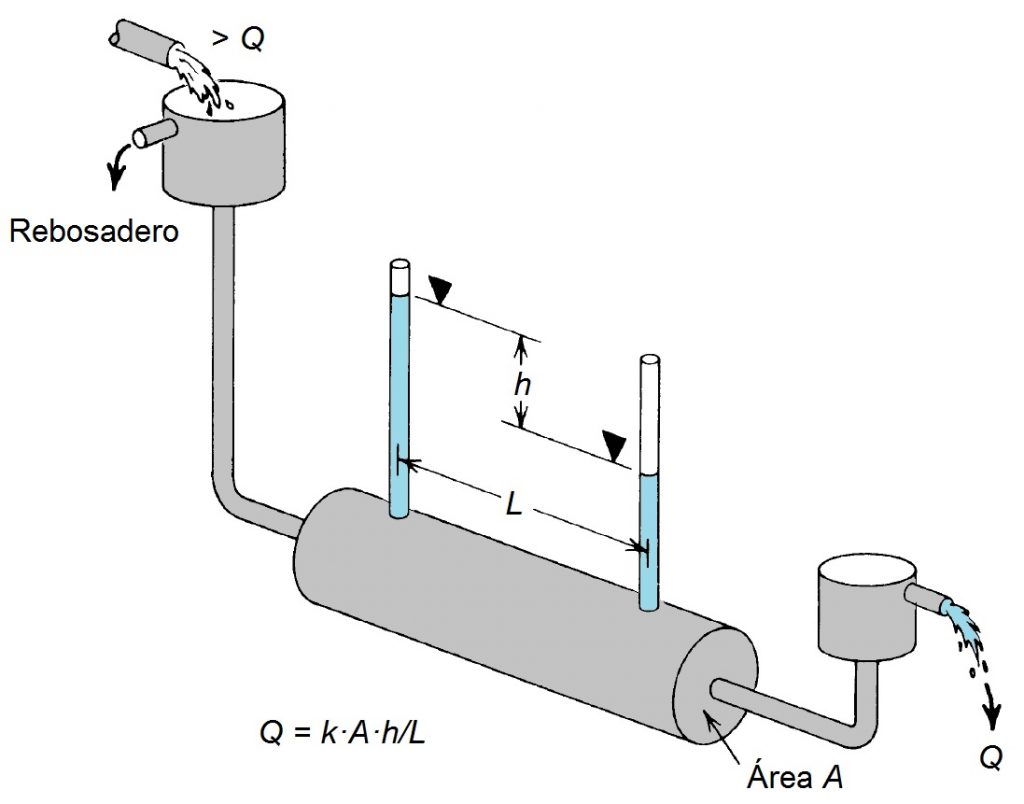
La Ley de Darcy es fundamental porque describe la velocidad del flujo de agua en un medio poroso. Establece que la velocidad (v) es directamente proporcional al gradiente hidráulico (i) y al coeficiente de permeabilidad (k), es decir, v = k · i. El coeficiente de permeabilidad mide la facilidad con la que el agua circula a través del suelo y depende tanto de las características del acuífero (porosidad, tamaño de los poros interconectados) como del fluido (viscosidad, peso específico). Esta ley es crucial para comprender cómo se mueve el agua a través del suelo y para calcular caudales en diversas aplicaciones geotécnicas.
3. ¿Qué son las tensiones efectivas y por qué son tan importantes en geotecnia según el postulado de Terzaghi?
Las tensiones efectivas (σ‘) son un concepto fundamental en geotecnia, postulado por Karl von Terzaghi en 1923. Se definen como el exceso de tensión sobre la presión intersticial (o presión neutra) del agua (u) presente en el suelo. Es decir, son las tensiones que actúan exclusivamente sobre la fase sólida del suelo, transmitiéndose grano a grano.
Su importancia radica en el postulado de Terzaghi, que establece lo siguiente: «Cualquier efecto medible debido a un cambio de tensiones, como la compresión, la distorsión o la modificación de la resistencia al corte de un suelo, se debe exclusivamente a cambios en las tensiones efectivas». Esto significa que la deformación y la resistencia del suelo dependen directamente de las tensiones efectivas y no de las tensiones totales. Por ejemplo, si el volumen o la distorsión de un suelo saturado no cambian, es porque sus tensiones efectivas no han cambiado. Si se permite el drenaje del agua (es decir, si se disipa la presión intersticial), las tensiones efectivas aumentan, lo que provoca la deformación del suelo y la modificación de su resistencia al corte, un fenómeno conocido como consolidación.
4. ¿Cuáles son los principales problemas geotécnicos relacionados con el agua en las excavaciones?
El agua subterránea y superficial puede causar diversos problemas geotécnicos significativos en las excavaciones:
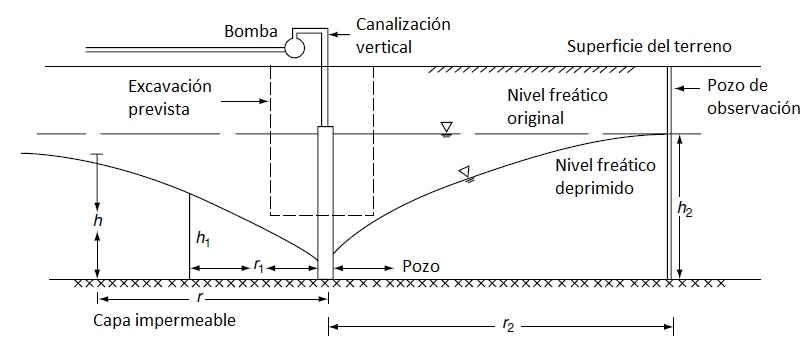
- Subsidencia: Un descenso del nivel freático (por bombeo o excavación) aumenta las tensiones efectivas, provocando asentamientos en el terreno circundante. Un aumento del freático también puede causar asentamientos en suelos arcillosos o reducir la capacidad portante en arenas.
- Deslizamiento de taludes: El flujo de agua en los taludes de una excavación incrementa su peso y reduce su resistencia al corte, llevando a la inestabilidad. Esto se agrava si la excavación corta dos estratos, donde el flujo entre capas puede causar erosión.
- Erosión superficial: El afloramiento de agua en los taludes provoca cárcavas y arrastre de terreno, lo que compromete la estabilidad y debilita las bermas.
- Erosión interna o tubificación (piping): El agua arrastra partículas finas a través de los huecos del suelo, formando túneles internos. Esto es propenso en suelos dispersables y puede ocurrir en presas o por flujos anómalos en pozos de drenaje o anclajes defectuosos.
- Inestabilidad del fondo o sifonamiento: Ocurre cuando un flujo ascendente de agua en un terreno granular no consolidado anula la presión efectiva, por lo que el suelo se comporta como un fluido (arenas movedizas). Esto sucede cuando las fuerzas de filtración superan el peso sumergido del suelo.
- Levantamiento del fondo o taponazo (uplift): El fondo de la excavación se vuelve inestable cuando el empuje del agua subterránea —típico en un acuífero confinado bajo un estrato de baja permeabilidad— supera el peso del terreno que lo soporta.
5. ¿Qué es el sifonamiento o «efecto Renard» y cuándo ocurre?
El sifonamiento, también conocido como licuefacción o «efecto Renard», se produce cuando existe un flujo ascendente de agua en el terreno y la presión del agua es tan alta que anula las tensiones efectivas del suelo. En suelos granulares sin cohesión, como la arena, el terreno pierde completamente su resistencia al corte y comienza a comportarse como un fluido en ebullición, similar a las arenas movedizas.
Este fenómeno sucede cuando se alcanza un «gradiente crítico», que es la relación entre el peso específico sumergido del suelo y el peso específico del agua. Si se sitúa un objeto con un peso específico superior al de la mezcla fluida de terreno y agua sobre un terreno con licuefacción, se hundirá. Supone un grave riesgo en las excavaciones, especialmente por debajo del nivel freático, ya que puede provocar el desprendimiento de cimentaciones y maquinaria.
6. ¿Cómo se relaciona el coeficiente de permeabilidad con la permeabilidad equivalente en estratos de suelo?
El coeficiente de permeabilidad (k) mide la facilidad con la que el agua fluye a través de un suelo concreto. Sin embargo, en la práctica, el suelo suele estar compuesto por múltiples estratos con diferentes permeabilidades y espesores. En estos casos, se calcula una permeabilidad equivalente, que puede ser horizontal o vertical:
- Permeabilidad equivalente horizontal: Se aplica cuando el flujo de agua atraviesa horizontalmente un conjunto de estratos. El caudal total es la suma de los caudales en cada estrato.
- Permeabilidad equivalente vertical: Se usa cuando el flujo de agua atraviesa verticalmente los estratos. En este caso, el caudal es constante a lo largo de los estratos, pero cada estrato tiene un gradiente hidráulico diferente.
Estos cálculos son esenciales para modelar con precisión el flujo de agua en suelos estratificados.
7. ¿Qué es una red de flujo y para qué se utiliza en geotecnia?
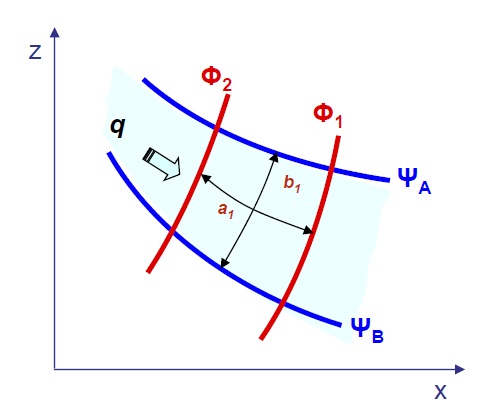
Una red de flujo es una representación gráfica del flujo de agua subterránea en un medio poroso. Está formada por dos familias de curvas ortogonales entre sí.
- Líneas equipotenciales (Ψ): Son líneas que conectan puntos donde la altura piezométrica (carga hidráulica) es constante.
- Líneas de corriente (Φ): Son las trayectorias que siguen las partículas de fluido a medida que se mueven a través del suelo.
La red de flujo se construye de manera que las fronteras impermeables actúan como líneas de corriente y las fronteras permeables (como una lámina de agua) son líneas equipotenciales. Al intersectarse, ambas familias de líneas deben formar «cuadrados curvilíneos».
Las principales aplicaciones de las redes de flujo en geotecnia son:
- Calcular las presiones del agua subterránea: Permiten determinar las presiones en diferentes puntos o superficies.
- Estimar los caudales del agua subterránea: Todos los canales de flujo (espacio entre dos líneas de corriente adyacentes) transportan el mismo caudal.
- Calcular los gradientes hidráulicos: La pérdida de carga total se distribuye uniformemente entre las equipotenciales. Esto es crucial para evaluar la estabilidad de taludes y el riesgo de sifonamiento.
8. ¿Cómo se puede prevenir el sifonamiento en una excavación y qué factores influyen en las medidas de prevención?
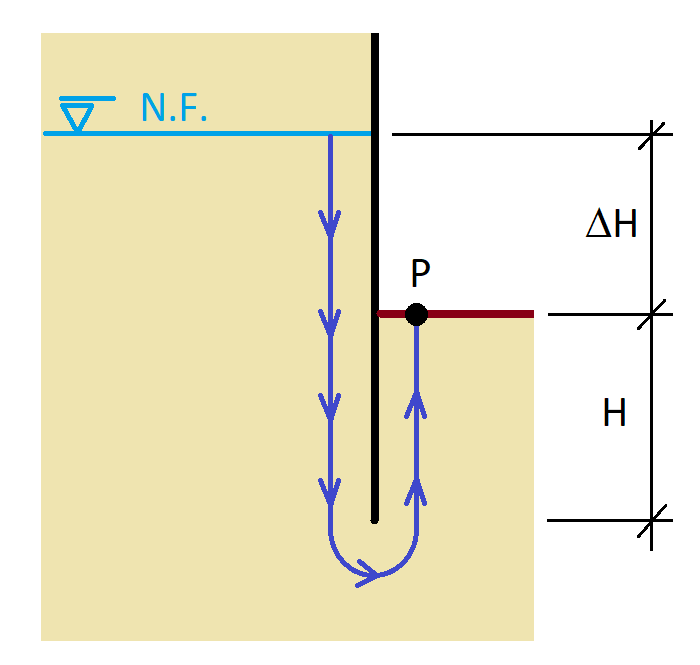
Para prevenir el sifonamiento en una excavación, especialmente por debajo del nivel freático, una de las medidas principales es utilizar tablestacas o ataguías con una longitud de empotramiento suficiente. Esta longitud adicional por debajo del nivel de excavación aumenta el recorrido más corto que puede seguir el agua, lo que reduce el gradiente hidráulico y, en consecuencia, las fuerzas de filtración.
La profundidad de empotramiento necesaria depende de varios factores:
- Profundidad de la excavación bajo el nivel freático: A mayor profundidad de excavación, mayor empotramiento se requiere.
- Porosidad del suelo: Cuanto mayor es la porosidad del terreno (es decir, más vacíos hay en el suelo), mayor empotramiento es necesario para evitar el sifonamiento.
- Peso específico de las partículas sólidas y del agua: Estos valores influyen en el peso específico sumergido del suelo y, por ende, en el gradiente crítico.
- Coeficiente de seguridad (η): Se aplica un coeficiente de seguridad para garantizar que el empotramiento sea suficiente para resistir el sifonamiento. Por ejemplo, el Código Técnico de la Edificación (CTE) en España recomienda un coeficiente de seguridad de η = 2 para pantallas.
Es fundamental realizar cálculos geotécnicos y estructurales detallados para determinar el empotramiento necesario, que debe corresponder al mayor valor entre el requerido para evitar el sifonamiento y el necesario para soportar los esfuerzos de empuje. Además, la experiencia y el sentido común son fundamentales a la hora de implementar estas medidas.
REFERENCIAS:
- PÉREZ VALCÁRCEL, J.B. (2004). Excavaciones urbanas y estructuras de contención. Ediciones Cat, Colegio Oficial de Arquitectos de Galicia, 419 pp.
- POWERS, J.P. (1992). Construction dewatering: New methods and applications. Ed. Wiley et al., New York.
- PREENE, M.; ROBERTS, T.O.L.; POWRIE, W., DYER, M.R. (2004). Groundwater control: design and practice. CIRIA C515, London.
- TOMLINSON, M.J. (1982). Diseño y construcción de cimientos. URMO, S.A. de Ediciones, Bilbao, 825 pp.
- YEPES, V. (2020). Procedimientos de construcción de cimentaciones y estructuras de contención. Colección Manual de Referencia, 2ª edición. Editorial Universitat Politècnica de València, 480 pp. Ref. 328. ISBN: 978-84-9048-903-1.
- YEPES, V. (2023). Maquinaria y procedimientos de construcción. Problemas resueltos. Colección Académica. Editorial Universitat Politècnica de València, 562 pp. Ref. 376. ISBN 978-84-1396-174-3
Cursos:

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.